ФОЭ2A. Статистика носителей заряда в полупроводниках глава 2

• Название: Статистика носителей заряда в полупроводниках глава 2
• Дата: 14.11.2022
• Размер: 0.99 Mb.
• Имя файла: ФОЭ2A.doc
• Тип: Глава; #788133
• страница: 2 из 7

2.2. Расчет положения уровня Ферми в собственном полупроводнике

Рассчитаем температурную зависимость положения уровня Ферми в собственном полупроводнике из очевидного равенства
.

Возьмем натуральный логарифм от обеих частей этого равенства:

.

Решая полученное уравнение относительно энергии W_F получаем следующее выражение для определения положения уровня Ферми в собственном полупроводнике:

, (2.15)

где W_i=(W_c+W_v)/2 - энергия, соответствующая положению середины запрещенной зоны полупроводника.

Поскольку , то в результате подстановки этого отношения в выражение (2.15) получаем, что

. (2.16)

Из выражения (2.16) следует, что в собственном полупроводнике при температуре абсолютного нуля уровень Ферми W_Fнаходится вблизи середины запрещенной зоны. При повышении температуры положение W_F смещается к краю одной из разрешенных зон. Направление смещения зависит от отношения эффективных масс носителей заряда.

Г 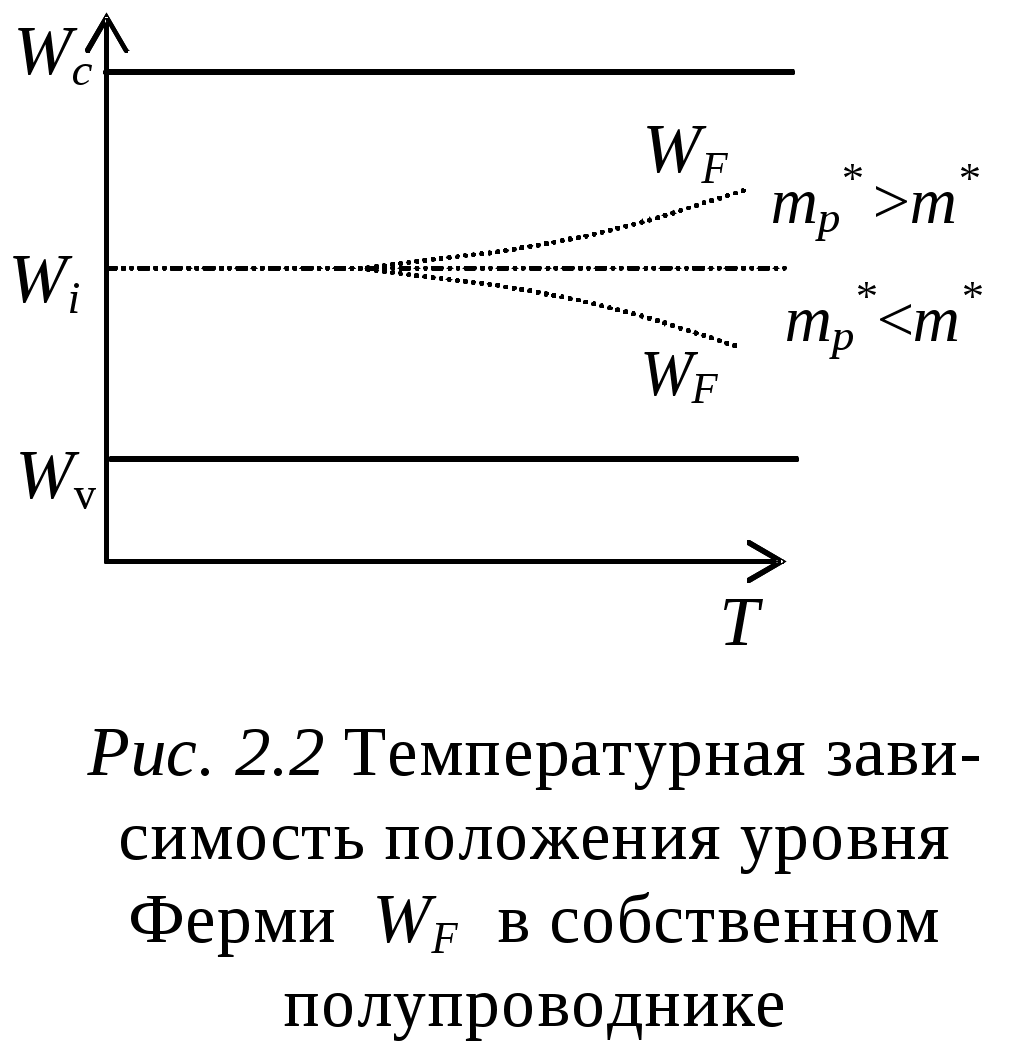рафик функции (2.16) представлен на рис. 2.2, откуда следует, что с ростом температуры Т положение уровня Ферми смещается вверх в направлении зоны проводимости, если эффективная масса дырок в полупроводнике превышает эффективную массу электронов, как это имеет место в Si. Напротив, если эффективная масса электронов превышает эффективную массу дырок, то положение уровня Ферми в таком полупроводнике смещается вниз в направлении валентной зоны.

Полупроводниковые материалы с собственной проводимостью находят ограниченное практическое применение в связи с трудностями, связанными с глубокой очисткой полупроводника. Вместе с тем, при определенных условиях, собственная проводимость часто наблюдается в полупроводниках, например, на границе контакта двух различных полупроводников или при контакте полупроводника с диэлектриком или металлом.

2.3. Расчет концентрации электронов и положения уровня Ферми в электронном полупроводнике

Для упрощения дальнейшего изложения воспользуемся приближенными методами анализа статистики электронов в полупроводнике. Предположим, что при комнатной температуре проводимость электронного полупроводника определяется, главным образом, электронами, образовавшимися при ионизации донорной примеси. Электроны в полупроводниках n - типа проводимости называют основными носителями заряда, а дырки - неосновными носителями заряда.

Каждый ионизированный атом донорной примеси (донор) можно рассматривать как примесный центр, захвативший дырку. Поэтому первое уравнение электронейтральности (2.3) для электронного полупроводника приобретает следующий вид:

n_n= , (2.17)

где n_n - концентрация свободных электронов в зоне проводимости полупроводника, м^-3; - концентрация ионизированных доноров на примесных уровнях, м^-3.

Умножая левую и правую части уравнения (2.17) на значение n_n и решая полученное уравнение относительно n_n, получим выражение для закона действующих масс в электронном полупроводнике в виде , откуда следует, что концентрация электронов в полупроводнике n-типа проводимости определяется уравнением вида

. (2.18)

Для определения концентрации электронов n_n и концентрации положительных ионов в электронном полупроводнике применяется тот же метод, что и для расчета концентраций электронов и дырок в собственном полупроводнике, рассмотренный выше в разделе 2.2. В результате получим, что концентрация электронов в электронном полупроводнике рассчитывается по формуле, аналогичной (2.11):

. (2.19)

Концентрация положительных ионов на примесных уровнях в электронном полупроводнике определяется по формуле, аналогичной (2.12):

, (2.20)

где N_d- эффективная плотность состояний дырок на уровнях W_dдонорной примеси, фактически представляющая концентрацию атомов донорной примеси, м^-3.

Подставив значения n_n и из выражений (2.19) и ( 2.20) в уравнение (2.18) получим , что концентрация электронов в электронном полупроводнике рассчитывается по формуле

, (2.21)

где W_d= W_c-W_d - энергия ионизации донорного уровня.

Формула (2.21) справедлива при расчетах концентрации основных носителей заряда в электронных полупроводниках для ограниченного диапазона температур от 0 до 30...70 К.

Это связано с тем, что при некоторой температуре Т_s, называемой температурой истощения, все атомы донорной примеси ионизируются, и дальнейшее увеличение температуры не приводит к возрастанию концентрации основных носителей заряда (электронов). Однако при значительном нагреве электронного полупроводника до температуры Т_i, называемой температурой появления собственной проводимости, концентрация электронов в зоне проводимости опять начинает расти, на этот раз вследствие тепловой генерации электронов из валентной зоны в зону проводимости.

Значение температуры истощения Т=Т_s можно рассчитать из формулы (2.21) полагая, что n_n=N_d. В результате логарифмирования и проведения соответствующих преобразований получим, что

. (2.22)

Аналогичным образом можно оценить и температуру появления собственной проводимости Т=Т_i, подставив в левую часть формулы (2.19) значение n_i=N_d. Выполнив соответствующие преобразования, получим формулу для расчета значения Т_i в виде

. (2.23)

Полагая, что для кремния значения величин под знаком натурального логарифма в формуле (2.22) находятся в пределах 10³...10⁴, в формуле (2.23) - в диапазоне 10⁶...10⁸, получим для величины Т_sзначение около 50...70 К, а для Т_i - 700...900 К, что примерно соответствует экспериментальным данным.

Т 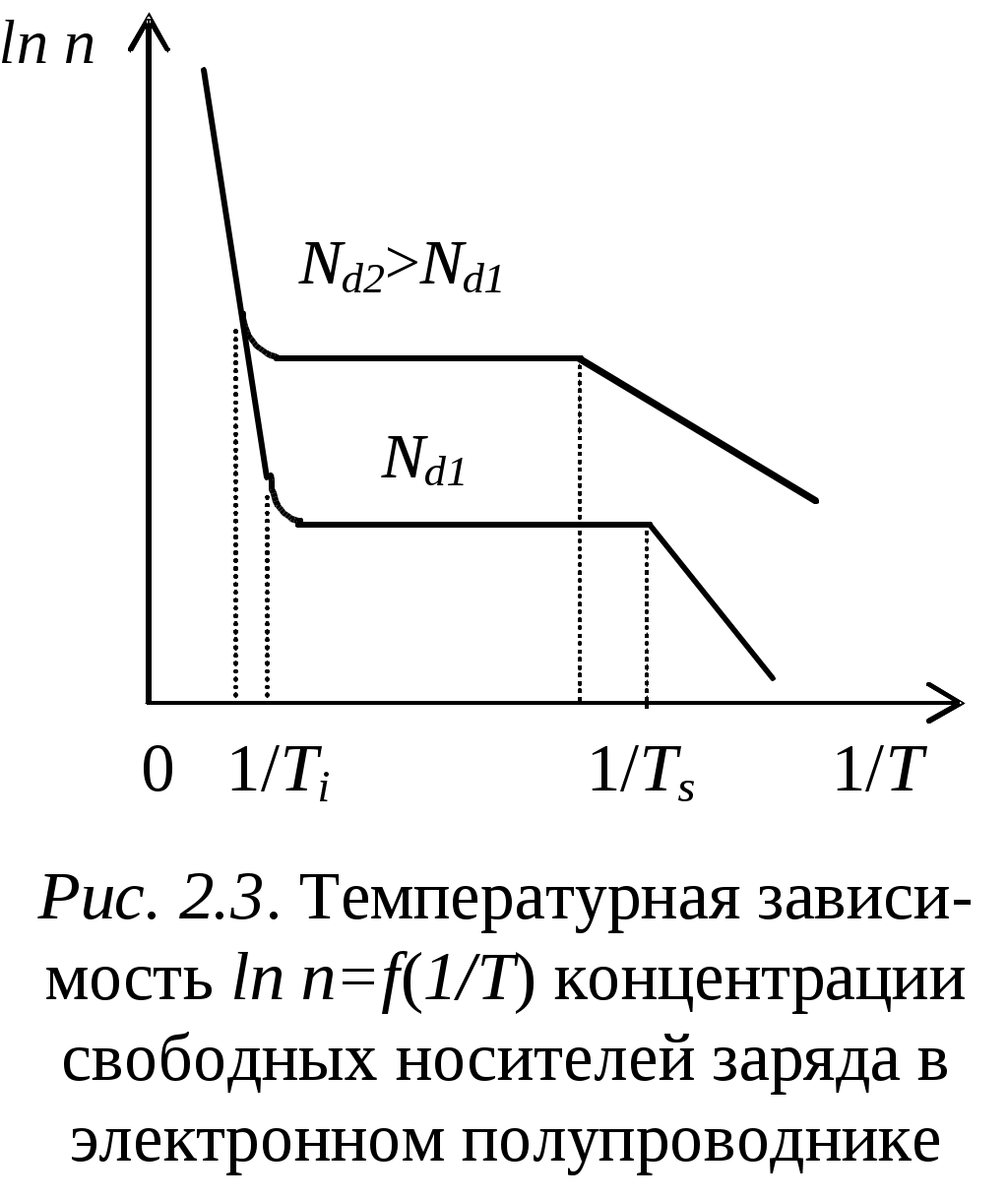емпературная зависимость концентрации носителей заряда n, в полупроводнике n-типа, построенная в координатах ln n=f(1/T), представлена на рис. 2.3. Из рис. 2.3 видно, что при повышении температуры полупроводника до температуры истощения Т_s электроны с примесных уровней переходят в зону проводимости. Область температур T T_s носит название области слабой ионизации.

При дальнейшем повышении температуры, вплоть до температуры появления собственной проводимости Т_i, концентрация собственных носителей заряда будет оставаться постоянной до тех пор, пока не станет заметным возбуждение и переход электронов из валентной зоны в зону проводимости. Область температур T_s T T_i называется областью истощения (областью сильной ионизации), для которой характерна полная ионизация всех атомов, заселяющих донорные уровни в полупроводнике. Наконец, область температур T T_i характеризует область перехода к собственной проводимости.

Из рис. 2.3 следует также, что чем больше концентрация донорной примеси N_d, тем выше температуры Т_i и Т_s, при которых концентрации собственных носителей заряда n становятся сравнимыми с концентрацией электронов, появившихся в зоне проводимости за счет полной ионизации атомов донорной примеси, то есть выполнения условия n=N_d.

Для определения положения уровня Ферми в электронном полупроводнике воспользуемся очевидным равенством n_n= , справедливым в диапазоне комнатных температур Т=300 К. Подставляя в это равенство значения n_n и из выражений (2.19) и (2.20) и беря натуральные логарифмы от левой и правой частей, получим следующее выражение

. (2.24)

Из этого выражения получаем, что значение энергии, соответствующей положению уровня Ферми W_F в электронном полупроводнике, рассчитывается по формуле

. (2.25)

График функции W_F=f(T) представлен на рис. 2.4, из которого можно сделать следующие выводы.

П 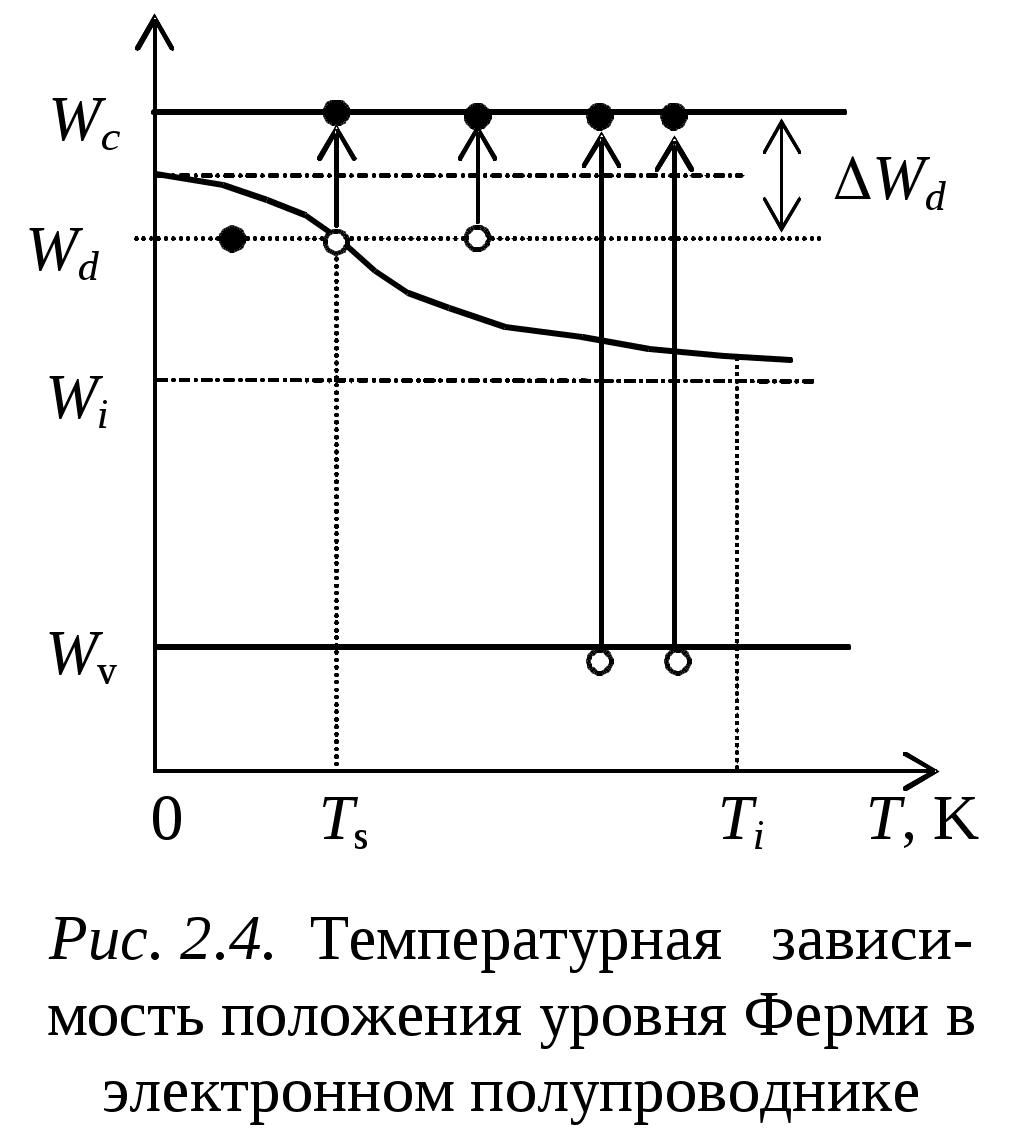ри Т=0 уровень Ферми в электронном полупроводнике располагается посередине между дном зоны проводимости и уровнем донорной примеси, то есть W_F=W_d+W_c)/2.

При возрастании температуры положение уровня Ферми W_F постепенно начинает снижаться и при температуре истощения Т=Т_s пересекает уровень донорной примеси W_d. Поскольку W_F=W_d, то равенство (2.24) можно записать в виде lnN_d=lnN_c-(W_c-W_F)/kT, откуда следует, что

. (2.26)

Подставляя в выражение (2.26) значение T=Т_s из формулы (2.22) и учитывая, что W_d=W_c-W_d, действительно получаем, что W_F=W_d.

При температурах, больших температуры истощения Т_s, положение уровня Ферми смещается вниз к середине запрещенной зоны, что свидетельствует о постепенном переходе от электронной к собственной проводимости полупроводника.

Для полупроводников n-типа в диапазоне температур области истощения T_s T T_i концентрация основных носителей (электронов), n_n=N_d, а дырок (неосновных носителей) согласно закону равновесия масс

. (2.27)

Увеличение концентрации доноров, N_d, приводит не только к увеличению концентрации электронов, но и к снижению концентрации дырок, p_n, из-за увеличения вероятности рекомбинации, скорость которой согласно (2.1) пропорциональна произведению концентраций электронов и дырок. Концентрация неосновных носителей обычно очень мала, но резко растет с температурой. Например, в кремнии при Т=300 К и N_d=10²² м^-3 значение p_n=2·10¹⁰ м^-3, а при увеличении Т на 100 К p_n вырастает на 6 порядков и составит 2·10¹⁶ м^-3. Несмотря на малые значения концентраций, неосновные носители влияют на важные параметры многих приборов (например, обратные токи в диодах).