ФОЭ2A. Статистика носителей заряда в полупроводниках глава 2

• Название: Статистика носителей заряда в полупроводниках глава 2
• Дата: 14.11.2022
• Размер: 0.99 Mb.
• Имя файла: ФОЭ2A.doc
• Тип: Глава; #788133
• страница: 5 из 7

2.5.1. Непосредственная рекомбинация

Это одноступенчатый процесс, происходящий при прямом захвате электрона зоны проводимости дыркой из валентной зоны.

Реализацией механизма непосредственной рекомбинации является межзонная рекомбинация. Межзонная рекомбинация происходит при переходе свободного электрона из зоны проводимости в валентную зону на один из свободных энергетических уровней (рис. 2.6, а). В результате наблюдается исчезновение пары носителей заряда - свободного электрона и дырки.

В зависимости от материала полупроводника в процессе межзонной рекомбинации выделяется энергия в виде квантов света (фотонов) или тепловых квантов (фононов), как это условно показано на рис. 2.6, а. В первом случае рекомбинацию называют излучательной, во втором - безизлучательной.

Излучательная рекомбинациянаблюдается при прямых (вертикальных) межзонных переходах, происходящих с излучением фотона без изменения волнового числа электрона k=Р/ , как изображено на рис. 2.6, б. Если обозначить значение волнового числа электрона в зоне проводимости через k_c, а в валентной зоне через k_v, то разность этих значений при прямых переходах удовлетворяет соотношению k_c-k_v 0. Приближенное равенство нулю означает, что излучаемый фотон обладает конечным, хотя и малым, значением волнового числа k_ф=2/_ф.

Энергия, выделяемая в виде кванта света, равна разности уровней энергий дна зоны проводимости W_с и потолка валентной зоны W_v, т. е. ширине запрещенной зоны W_g полупроводника:

W_с-W_v=W_g=h, эВ, (2.42)

где - частота волны излучаемого кванта света, Гц.



Поскольку =с/_ф, где с=2,99810⁸ м/с - скорость света, то из (2.42) вытекает простая формула, позволяющая оценить длину волны _фиспускаемого излучения в процессе излучательной рекомбинации:

, мкм, (2.43)

где W_g - ширина запрещенной зоны, эВ.

При обычных значениях ширины запрещенной зоны полупроводников W_g, равных 1...1,5 эВ, оценка величины _ф по формуле (2.43) дает значение длины волны излучаемого фотона около 10^-6 м. Следовательно, величина k_ф (2...7)10⁶ м^-1, что значительно меньше волнового числа электрона k_n 10¹⁰ м^-1. Соответственно, значение импульса фотона Р_ф= k_ф почти на три порядка меньше импульса электронов Р_n= k_n, участвующих в процессе межзонной рекомбинации. Поскольку импульс фотона ничтожно мал, делаем вывод о том, что в межзонной излучательной рекомбинации могут участвовать только те электроны и дырки, импульсы Р которых имеют противоположные знаки и практически равны по величине.

Как отмечалось в п. 1.5.8, к прямозонным полупроводникам относятся GaAs, а также InSb и ряд других. Полупроводниковые материалы, в которых наблюдается эффект излучательной рекомбинации в p-n переходах, применяются для изготовления индикаторных устройств - светодиодов.

Безизлучательная рекомбинация - это процесс, наблюдаемый при непрямых межзонных переходах, происходящих с изменением волнового числа электрона, то есть в этом случае разность k_c-k_v 0 (рис. 2.6, б). Процесс безизлучательной рекомбинации сопровождается передачей части энергии, выделившейся при переходе электрона из зоны проводимости в валентную зону, кристаллической решетке в виде большого числа фононов с энергией . Часть энергии, выделившейся при рекомбинации, может быть передана соседнему (третьему) носителю заряда, что приводит к ударной ионизации и разрыву ковалентной связи носителя заряда с атомом полупроводника. Величину изменения энергии электрона при безизлучательной рекомбинации можно представить в виде выражения

W_c-W_v= . (2.44)

Безизлучательная рекомбинация наблюдается в непрямозонных полупроводниках, таких как Si, Ge, GaP и др.

Следует отметить, что процесс непосредственной межзонной рекомбинации в широкозонных полупроводниках маловероятен вследствие рассеяния энергии избыточных носителей на тепловых колебаниях решетки. Например, в Ge (W_g 0,67 эВ) вероятность межзонной рекомбинации составляет всего 10^-4. Механизм непосредственной рекомбинации является определяющим лишь в узкозонных полупроводниках с шириной запрещенной зоны W_g<0,3 эВ, таких, как PbS (W_g 0,1 эВ), InSb (W_g 0,18 эВ). Однако вероятность непосредственной рекомбинации существенно возрастает при высоких уровнях инжекции неосновных носителей заряда в полупроводнике, например при инжекции через p-n переход. Это обстоятельство используется, например, при изготовлении светодиодов.

Процессы непосредственной рекомбинации характеризуются дифференциальным уравнением рассасывания. Это уравнение представляет зависимость скорости убывания концентрации неравновесных носителей dn/dt и dp/dt, происходящей в результате выключения источника инжекции, от разности скорости рекомбинации неравновесных носителей R и скорости генерации равновесных носителей заряда G_o=rn_op_o. При этом предполагается, что в течение процесса рекомбинации выполняется условие электронейтральности полупроводника, то есть концентрации избыточных носителей заряда равны между собой (n=p). Исходя из сказанного, выражение для дифференциального уравнения рассасывания можно записать в виде

-dn/dt=-dp/dt=R-G_o=rnp-rn_op_o, (2.45)

где n=n_o+n, p=p_o+p - концентрации неравновесных носителей заряда в полупроводнике, причем n<<n_o, p<<p_o.

Отрицательный знак в левой части уравнения (2.45) указывает на уменьшение концентрации носителей в процессе рекомбинации.

Подставим значения концентраций неравновесных носителей n и p в уравнение (2.45). Решая это уравнение относительно dn/dt и учитывая, что произведение np 0 из-за малости n иp, получим следующее дифференциальное уравнение

dn/dt=-r(n_op+p_on+np) -r(n_o+p_o)n. (2.46)

Обозначим произведение r(n_o+p_o)=1/, где  - среднее время жизни неравновесных носителей заряда в полупроводнике. Подставляя это значение в уравнение (2.46), получим окончательный вид дифференциального уравнения рассасывания при непосредственной рекомбинации носителей заряда

. (2.47)

Записав это уравнение в виде d(n)/n=-dt/ и выполняя интегрирование, получим ln(n)=C-t/. В этом выражении С - постоянный коэффициент, численно равный логарифму концентрации неравновесных носителей заряда в начальный момент времени t=0, т. е. С=ln[n(0)]. Следовательно, решение дифференциального уравнения (2.47) имеет вид экспоненты и характеризует спад избыточной концентрации носителей заряда:

n(t)=n(0)exp(-t/). (2.48)

График функции (2.55) представлен на рис. 2.7. Из этого рисунка и уравнения (2.48) можно определить среднее время жизни носителей заряда в полупроводнике  как среднее время жизни избыточных носителей заряда, в течение которого их концентрация вследствие рекомбинации уменьшается в e 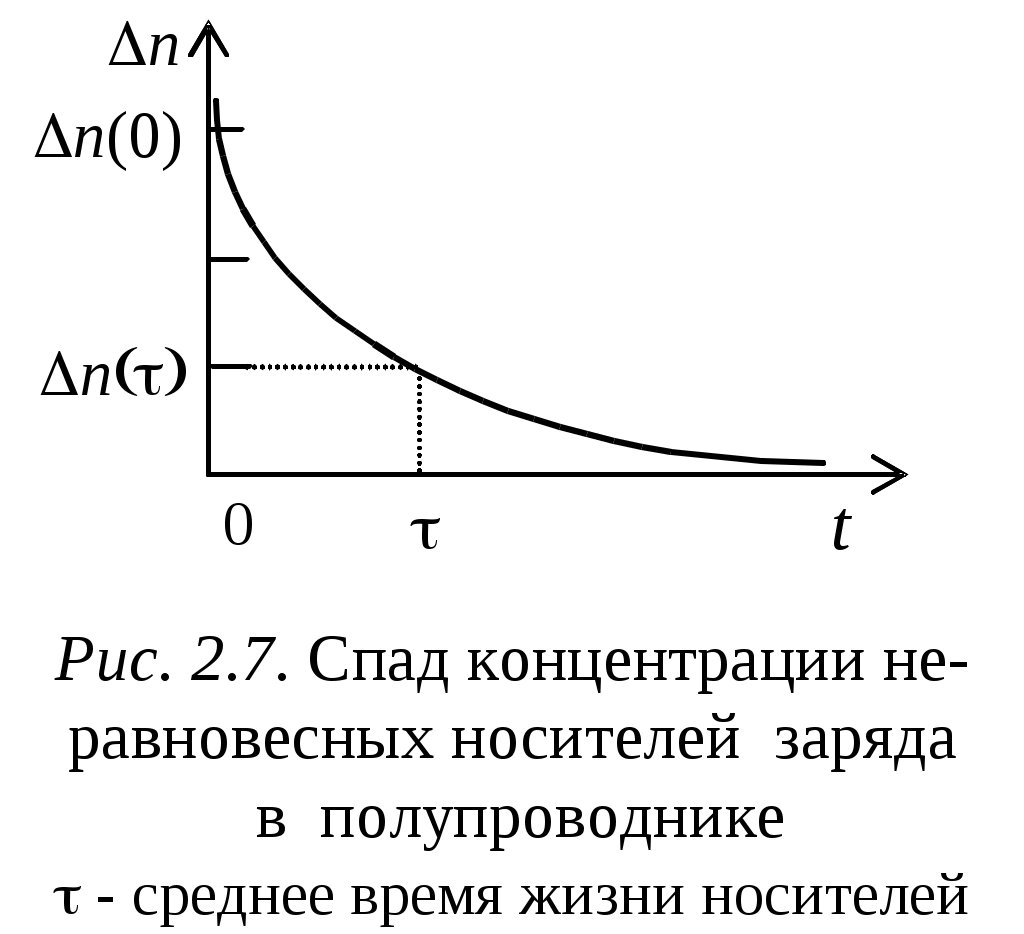2,73 раза.

Д ля собственного полупроводника, содержащего электроны и дырки, обратная величина среднего времени жизни неравновесных носителей заряда определяется соотношением 1/=rn_o+rp_o. Поэтому обратная величина времени жизни носителей в собственном полупроводнике складывается из обратных величин времен жизни электронов и дырок, то есть 1/=1/_p+1/_n.

Очевидно, для полупроводников с электронной проводимостью среднее время жизни носителей заряда определяется средним временем жизни неосновных носителей заряда (дырок), т. е. =_p, а для дырочных полупроводников, наоборот, - временем жизни электронов, =_n. В реальных полупроводниках измеренное на опыте время жизни неравновесных носителей заряда достигает 10^-7...10^-6 сек.