План лекц.. Строение вещества. I. Строение атома

• Название: Строение вещества. I. Строение атома
• Анкор: План лекц..doc
• Дата: 11.01.2018
• Размер: 14.08 Mb.
• Имя файла: План лекц..doc
• Тип: Документы; #13867
• страница: 8 из 17

Для многих соединений не удается осуществить реакцию их образования из простых веществ и тем более измерить теплоту образования. Но! В большинстве случаев можно осуществить реакцию полного сгорания.

Стандартная теплота сгорания (∆Н_c⁰) – это теплота, вы-деляющаяся при сгорании в атмосфере кислорода 1 моль вещества при ст. давлении 1,013^.10⁵ Па до простых оксидов

При этом все участники реакции должны быть в устойчи-вых агрегатных состояниях.

Пример: рассчитать тепловой эффект горения спирта:

С₂Н₅ОН + 3 О₂ = 2 СО₂ + 3 Н₂О

Решение:

∆Н_х.р= ∆Н_c⁰(С₂Н₅ОН) + 3∆Н_c⁰(О₂) - 2∆Н_c⁰(СО₂) - 3∆Н_c⁰(Н₂О)

Далее находим (в таблицах термодинамических величин) стандартные теплоты сгорания ∆Н_c⁰ всех веществ и определяем ∆Н_х.р .
Следствие 4. Если совершаются две реакции, приводящие из различных начальных состояний к одинаковым конечным состояниям, то разность между их тепловыми эффектами равна тепловому эффекту перехода системы из одного состояния в другое.

Это следствие позволяет точно вычислять тепловые эффекты процессов, которые мы даже не имеем возможности осуществить практически.
Пример (классический!):

Определить тепловой эффект превращения графита в алмаз: С (графит) → С (алмаз).

Решение: определим неизвестный тепловой эффект (∆Н_х) путем анализа реакций горения графита и алмаза по закону Гесса: С (графит) + О₂ = СО₂ + 393, 51 кДж (1)

С (алмаз) + О₂ = СО₂ + 395, 34 кДж (2)

С (графит) → С (алмаз) = (1) – (2)

∆Н₁ = - Q = - 393, 51 кДж; ∆Н₂ = - 395, 34 кДж

∆Н_х= ∆Н₁ - ∆Н₂ = 395, 34 - 393, 51= + 1, 83 (кДж)

Таким образом, переход графита в алмаз сопровождается поглощением сравнительно небольшого количества теплоты.

Примеры решения типовых задач

Задача 1.

Рассчитать теплоту образования CuCl₂ по реакции: Cu_(T)+ Cl_2(T)= CuCl_2(T) при 500С, если ∆H₂₉₈(CuCl_2(T)) = –205,9 кДж/моль, а молярные теплоемкости веществ имеют следующие значения :

C_p(Cu_(T))=22,6 + 6,28·10^-3·T Дж/(моль·К);

C_p(Cl₂)=36,7 + 1,05·10^-3·T Дж/(моль·К);

C_p(CuCl_2(T))=64,5 + 50,2·10^-3·T Дж/(моль·К);

Решение.

Используем уравнение Кирхгоффа где

∆C_p= C_p(CuCl₂)–(C_p(Cu_(T))+ C_p(Cl_2(T))).

Найдем ∆C_p:

∆C_p=64,5 + 50,2·10^-3·T –22,6 – 6,28·10^-3·T – 36,7 + 1,05·10^-3·T;

∆C_p=5,2 + 42,9·10^-3·T 

Представим ∆C_p выражением ∆C_p= a + bT, где a = 5,2; b = 42,9·10^-3.

Определим теплоту образования CuCl₂ при температуре 500С или 773 К:

.

Подставляя числовые значения a, b, T, ∆H₂₉₈ (из условия задачи), получим: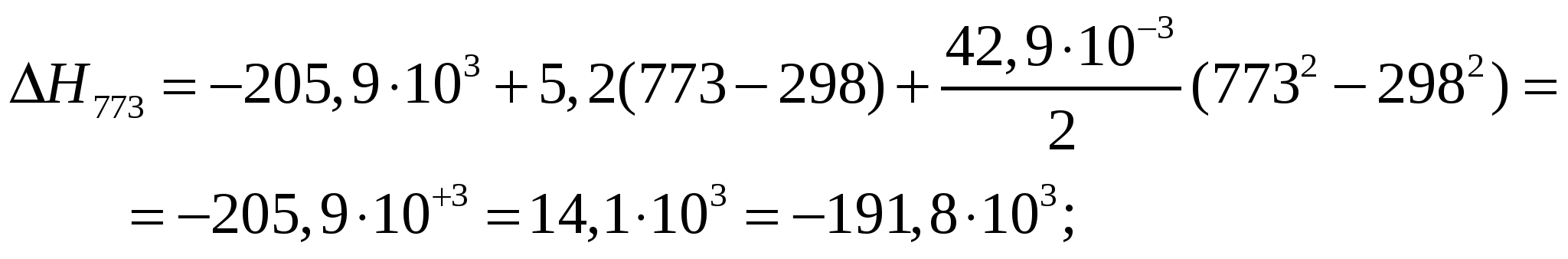



∆H₇₇₃=–191,8 (кДж/моль).
Процессы в живых организмах

В человеческом организме идут многочисленные химические превращения (под общим названием «обмен веществ» или «метаболизм»), каждое из кото-рых сопровождается изменениями внутренней энергии и энтальпии организма.

Основные источники энергии для человека – пища и вода (напитки). По сравнению с этим энергия, поступающая в тело человека в виде тепла (например, когда греемся у печки, костра) – ничтожно мала.

Энергию организму дают, как известно, основные компоненты любой пищи: жиры (38 ккал/г), белки (17 ккал/г), углеводы (16 ккал/г). Организмом расходуется большая часть этой энергии, причем точное ее значе-ние зависит от возраста, пола, роста, веса и вида деяте-льности человека. Мужчины расходуют ежедневно от 9200 до 12100 кДж, женщины – от 6700 до 8800 кДж.

Если поглощается энергии больше, чем тратится, то ее избыток запасается в теле в виде жира. Каж-дый 1 г жира образуется за счет избыточной энер-гии, равной ≈ 35000 кДж.

(см.: Коровин. Химия – с.128-130. Калорийность пищи)

Теплоемкость

- количество теплоты, необходимое для нагрева единицы массы (в граммах) или количества вещества (моль) на единицу температуры (на 1 градус Цельсия , 1 Кельвин ).

Различают удельную, мольную (молярную), истинную, среднюю теплоемкости.

Удельная теплоемкость определяется количеством теплоты, необходимым для нагрева 1 г вещества на 1 К.

Мольная теплоемкость определяется количеством теплоты, необходимым для нагрева 1 моля вещества на 1 К.

Средняя теплоемкость – количество теплоты, необходимое для нагрева единицы количества вещества от Т₁ до Т₂:



Истинная теплоемкость определяется выражением: ,

где dQ и dТ – бесконечно малые приращения теплоты и температуры.

Связь между средней и истинной теплоемкостью определяется выражением:



Различают теплоемкостипри постоянном давлении С_р (изобарная)и при постоянном объеме С_V (изохорная).

ПосколькуQ_p = ∆H при р = const, а Q_V = ∆U при V = const, то

, .

Связь между С_р и С_Vопределяется выражением: С_р - С_V= R,

где R - универсальная газовая постоянная, R = 8,314 Дж/моль∙К.

Правило Дюлонга-Пти

Атомная теплоемкость химических элементов (С_ат) в твердом состоянии, т.е. произведение атомной массы (А) элемента наего удельную теплоемкость (С_уд) приблизительно одинакова для всех элементов и равна ≈ 25 Дж/моль ^.К: С_ат = А_r^.С_уд ≈ 25,1 Дж/моль ^.К,

При этом С_p(ат) = А_r^.С_p= 25,1 Дж/моль ^.К,

С_V (ат) =А_r ^.С_V = 24,85 Дж/моль ^.К

Правило Неймана - Коппа (аддитивности)

Молярная теплоемкость (С_мол) химических сое-динений в твердом состоянии, т.е. произведение их молекулярной массы (М_r) на удельную теплоем-кость, равна сумме атомных теплоемкостей химических элементов, входящих в данное соединение: С_мол = М_r^.С_уд = ∑С_ат (N_атомов), т.е.

С_мол = С_ат (1) + С_ат(2) + …+ С_ат (N), Дж/моль ^.К
Зависимость теплового эффекта реакции от темпе-ратуры (при постоянном давлении или объеме) определяется уравнением (законом) Кирхгоффа:

где

- тепловой эффект реакции при данной температуре,

- тепловой эффект при Т = 298 К (стандартной).

∆С_р для условного уравнения реакции: аА + bВ = сС + dD определяется так: где

С_р(А),, С_р(В), С_р(С), С_р(D) – мольные теплоемкости веществ А, В, С, D при р = const;

∆С_р - общее изменение в реакции мольных теплоемкостей веществ А, В, С, D; a, b, c, d – стехиометрические коэффициенты для этих веществ в уравнении данной химической реакции.

Второе начало (закон) термодинамики

Значение второго начала

Все процессы можно разбить на две группы:

1. Процессы, не требующие затраты энергии извне,

в результате которых может быть совершена работа против внешних сил – самопроизвольные процессы;

2. Процессы, для осуществления которых требуют-ся затраты энергии извне - несамопроизвольные про-цессы (подъем груза, переход тепла от горячего тела к холодному, разложение воды на водород и кислород…)

1-е начало термодинамики позволяет составить энергетический баланс системы или процесса. С помощью закона Гесса, основного закона термохимии, и его следствий, можно рассчитать тепловые эффекты как самопроизвольных и несамопроизвольных реакций, так и вообще реально не осуществимых.

2-е начало т/д-ки:

1) позволяет установить принципиальную осуществи-мость интересующего нас процесса;

2) определяет, какие из процессов в данной системе при заданных условиях могут протекать самопроизво-льно – т.е. вводит критерий самопроизвольного протекания того или иного процесса;

3) устанавливает предел самопроизвольного протека-ния того или иного процесса, т.е. состояния равновесия

4) дает возможность определить внешние условия для протекания интересующего нас процесса в нужном направлении и в нужной степени

– все это имеет большое значение для решения множества научных и технологических задач.

Второе начало термодинамики, вместе с первым началом, устанавливает точные количественные соотношения между различными макроскопическими параметрами систем в состоянии термодинамического равновесия.

Формулировкавторого закона термодинамики Клаузиуса Р. (1850 г.):

а) Невозможен процесс, при котором теплота переходила бы от тел более холодных к телам более нагретым.

Для количественной оценки степени необратимости реальных процессов Клаузиус Р. (1865 г.) ввел новую т/д-кую величину, названную им «энтропия» (от греч. «поворот, превращение»).

Энтропия (S) – величина, изменение которой в ходе равновесного процесса при изотермическом сообщении системе некоторого количества теплоты равно отношению теплового эффекта этого процесса (Q, ∆Н) к абсолютной температуре (Т):

∆S > ∆Н / Т (при р,Т = const).

(При этом знак = относится к обратимым процессам, а знак > - к необратимым)

Энтропия – т/д-кая функция состояния системы, определяющая меру вероятности состояния, разупорядоченности (хаоса) системы. Как любая функция состояния, энтропия не зависит от пути процесса и определяется начальным и конечным состояниями системы.

Энтропия в разных формулировках выражает суть второго закона (начала) термодинамики.

Предложено несколько формулировок второго начала.

1. Согласно Клаузиусу Р. (1850 г.):

а) В изолированных системах (Q=0, А=0, U= сопst) самопроизвольно идут только те процессы, которые сопровождаются ростом энтропии системы, т.е. ∆S > 0.

Иначе: изолированная система всегда стремится достичь состояния с максимальной энтропией (максимальным беспорядком), т.е состояния термодинамического равновесия.

б) Любой самопроизвольный процесспротекает в направлении, при котором система переходит из менее вероятного состояния в более вероятное, сопровождающееся увеличением энтропии, т.е.

∆S > 0.

Энтропия – мера приближения системы к равновесию

Равновесное состояние является наиболее вероятным состоянием любой системы, и в этом состоянии ееэнтропиямаксимальна.

2. Энтропию как меру хаотичности системы, ее разупорядоченности определяют выражением Л. Больцмана: S = RlnWили S = К_БlnW,

где R – универсальная газовая постоянная; К_Б – постоянная Больцмана (К_Б = R /N_A), W – т/д-кая вероятность состояния системы, равная числу мик-росостояний системы, т.е. числу возможных рас-пределений каждой ее частицы по координатам и скоростям (параметров положения и скорости каж-дой частицы системы) при данных температуре, объеме, давлении и количестве частиц.

Из выражения Больцмана следует: при повы-шении температуры энтропия возрастает, при охлаждении – уменьшается и при приближении к абсолютному нулю стремится к нулю. - Это и позволяет сделать вывод об энтропии как мере хаотичности, неупорядоченности системы.

Энтропия является аддитивной величиной: энтропия системы равна сумме значений энтропии ее компонентов (исключение составляют растворы).

Термодинамическая вероятность состояния системы в случае обратимых процессов остается постоянной: W₁ =W₂ и ∆S = 0

(W₁ и W₂ - т/д-кие вероятности состояний 1 и 2 системы, тогда lnW₁ = lnW₂ , W₁ / W₂= 1,ln(W₁ / W₂) = 0 и ∆S = 0).

В необратимых процессах W₁ < W₂,lnW₁ / lnW₂ < 1 и энтропия возрастает: ∆S > 0.

Это означает, что необратимый процесс переводит систему в более вероятное состояние.

Поскольку энтропия- мера хаотичности (разупорядоченности) системы, то она возрастает (∆S > 0) при переходе вещества в менее упорядоченное состояние: из кристаллического - в жидкое, из жидкого (или твердого) - в газообразное состояние, при растворении кристаллов, при расширении газов, при химических взаимодействиях, приводящих к увеличению числа частиц, и прежде всего - в газообразном состоянии.

Напротив, все процессы, в результате которых упорядоченность системы возрастает (конденсация, полимеризация, сжатие, уменьшение числа частиц), сопровождаются уменьшением энтропии (∆S < 0).