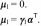Взять больше лагов, чем меньше. Однако этот последний аргумент верен только с асимптотической точки зрения

• Название: Взять больше лагов, чем меньше. Однако этот последний аргумент верен только с асимптотической точки зрения
• Дата: 31.03.2023
• Размер: 71.28 Kb.
• Имя файла: some.docx
• Тип: Документы; #1028523

взять больше лагов, чем меньше. Однако этот последний аргумент верен только с асимптотической точки зрения.

2) Другой подход состоит в том, чтобы выбирать L на основе обычных t­и F-статистик для соответствующих дополнительных регрессоров.

ADF может давать разные результаты в зависимости от того, каким вы­брано количество лагов. Даже добавление лага, который "не нужен" соглас­но только что приведенным критериям, может резко изменить результат тес­тирования.

Особую проблему создает наличие сезонной компоненты в переменной.

Если сезонность имеет детерминированный характер, то достаточно доба­вить в регрессию фиктивные сезонные переменные - это не изменяет асим­птотического распределения АDF-статистики. Для случая стохастической се­зонности также есть специальные модификации теста.

Пока мы рассмотрели тесты 1(1) против 1(0). Временной ряд может быть интегрированным и более высокого порядка. Как несложно понять, тесты 1(2) против 1(1) сводятся к рассмотренным, если взять не уровень тестируе­мого ряда, а первую разность. Аналогично для более высоких порядков ин­тегрирования.

Имитации показали, что следует проверять гипотезы последовательно, начиная с наиболее высокого порядка интегрирования, который можно ожи­дать априорно. Т. е., сначала следует проверить гипотезу о том, что ряд явля­ется 1(2), и лишь после этого, если гипотеза была отвергнута, что он является 1(1). (См. Dickey and Pantula, 1987.)

Коинтеграция. Регрессии с интегрированными переменными

Как уже говорилось выше, привычные методы регрессионного анализа не подходят, если переменные нестационарны. Однако не всегда при приме­нении МНК имеет место эффект ложной регрессии.

Говорят, что 1(1 )-процессы Y₁t е Y₂t является коинтегрированными первого порядка (Cl(l,O)), если существует их линейная комбинация, которая является 1(0), то есть стационарна. То есть Y₁t, Y₂t - 1(1 ), коинтегрированы,

если существует коэффициент л, такой что Y₁t-лY₂t - 1(0). Понятие коинте­грации введено Грейнджером (Granger(l981)).

Понятие коинтеграции тесно связано с моделью исправления ошибки.

Коинтегрированные процессы Y₁t ё Y₂t связаны между собой долгосрочным 41





стационарным соотношением, и следует предположить, что сушествует не­кий корректирующий механизм, который при отклонениях возвращает Y₁t е

Y₂t к их долгосрочному отношению.

Если л., =1, то разность Y₁t å Y₂t áóäåò ñòàöèîíàðíîé è, ãðóáî ãîâîðÿ, Y₁t å Y₂t áóäóò äâèãàòüñÿ "ïàðàëëåëüíî" âî âðåìåíè. Ñëåäóþùèé ðèñóíîê (Ðèñ. 7) èçîáðàæàåò äâå òàêèõ êîèíòåãðèðîâàííûõ ïåðåìåííûõ, äèíàìèêà êîòîðûõ çàäàíà ìîäåëüþ èñïðàâëåíèÿ îøèáêè:

x1t = х1 t-1 - 0.² (У1 t-1 - У2 t-1 + ²) + ⁸1t' y2t = у2 t-1 + о.э (У1 t-1 - у2 t-1+2)+⁸2t' s1t,s₂t NID(O,l).

Определение коинтеграции естественным образом распространяется на случай нескольких коинтегрированных переменных произвольного порядка

интегрирования. Компоненты п-мерного векторного процесса Yt = (Y₁t, ... ,Уп t) называют коинтегрированными порядка d, Ь, что обозначается Yt-CI(d,b), если (1) Yit является I(d) i= 1, ... , пи (2) существует отличный от нуля вектор /3, такой что Yt/3-I(d-b), d?::.b>O. Вектор /3 называют коинтегрирующим век­тором.

В рассмотренном ранее примере коинтеграционный вектор имеет вид /3=(-l,л). Его можно пронормировать также как (-1/л,1).

Если переменные в регрессии не стационарны, но действительно связа­ны друг с другом стационарной линейной комбинацией (модель специфици­рована верно), то полученные оценки коэффициентов этой линейной комби-





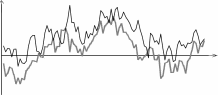
Рис. 7. Два коинтегрированных процесса при л.=1.

нации будут на самом деле сверхсостоятельными, то есть сходятся по веро-

42





ятности к истинным коэффициентам со скоростью, пропорциональной не квадратному корню количества наблюдений, как в регрессии со стационар­ными переменными, а со скоростью, пропорциональной просто количеству

наблюдений. Другими словами в обычной регрессии (i - л) имеет невы­рожденное асимптотическое распределение, а в регрессии с 1(1)-

переменными N(i - л) имеет невырожденное асимптотическое распределе­ние.

Обычные асимптотические аргументы сохраняют свою силу, если речь идет об оценках параметров краткосрочной динамики в модели исправления ошибок. Таким образом, можно использовать t-статистики, получаемые обычным методом наименьших квадратов, для проверки гипотез о значимо­сти отдельных переменных. Важно помнить, что это относится к оценкам краткосрочных параметров. Этот подход не годится для проверки гипотез о коэффициентов коинтеграционной комбинации.

Оценивание коинтеграционной регрессии: подход Энгла­Грейнджера

Если бы коэффициент л был известен, то проверка на коинтегрирован­ность была бы эквивалентна проверке Y₁t-лY₂t на стационарность. Но в практических проблемах обычно стационарная линейная комбинация неиз­вестна. Значит, необходимо оценить коинтегрирующий вектор. Следует так­же проверить, действительно ли этот вектор дает стационарную линейную комбинацию.

Простейшим методом отыскания стационарной линейной комбинации является метод Энгла-Грейнджера. Энгл и Грейнджер предложили использо­вать оценки, полученные из обычной регрессии с помощью метода наи­меньших квадратов. Одна из переменных должна стоять в левой части рег­рессии, другая - в правой:

Y1t= лУ₂/ -.

Для тестирования стационарности полученной линейная комбинации предлагается применить метод Дики-Фуллера к остаткам из коинтеграцион-

ной регрессии. Пусть - ut остатки из этой регрессии. Тест Энгла-Грейндже­ра проводится с помощью регрессии

ut= р И t-1 + остатки. 43



Распределение t-статистики для гипотезы р = 1 в этой регрессии будет отличаться (даже асимптотически), от распределения DF-статистики, но имеются соответствующие таблицы. Нулевой гипотезой, таким образом, яв­ляется отсутствие коинтеграции. Если мы отвергаем гипотезу об отсутствии коинтеграции, то это дает уверенность в том, что полученные результаты не являются ложной регрессией.

Игнорирование детерминированных компонент ведет к неверным выво­дам о коинтеграции. Чтобы этого избежать, в коинтеграционную регрессию следует добавить соответствующие переменные - константу, тренд, квадрат тренда, сезонные фиктивные переменные. Добавление константы, тренда, и квадрата тренда, как и в случае DF, меняет асимптотическое распределение теста Энгла-Грейнджера. Следует помнить, что, в отличие от DF, регрессия, из которой берется t-статистика, остается неизменной, то есть в нее не нужно добавлять детерминированные регрессоры.

В МНК регрессии с коинтегрированными переменными оценки должны быть смещенными из-за того, что в правой части стоит эндогенная перемен­ная, коррелированная с ошибкой. Кроме того, ошибка содержит пропущен­ные переменные. Коинтеграционная регрессия Энгла-Грейнджера является статической по форме, то есть не содержит лагов переменных. С асимптоти­ческой точки зрения не приводит к смещенности оценок, поскольку ошибка является величиной меньшего порядка, чем регрессор, дисперсия которого стремится к бесконечности. Как уже говорилось, оценки на самом деле сверхсостоятельны. Однако в малых выборках смещение может быть суще­ственным.

После того, как найдена стационарная линейная комбинация, можно оценить модель исправления ошибок, которая делает переменные коинтег­рированными. В этой регрессии нужно использовать первые разности ис­ходных переменных и остатки из коинтеграционной регрессии, которые бу­дут представлять корректирующий член модели исправления ошибок.

Подчеркнем роль корректирующего члена. До появления метода Энгла­Грейнджера исследователи часто оценивали регрессии в первых разностях, что, хотя и приводило к стационарности переменных, но не учитывался ста­ционарный корректирующий член, то есть регрессионная модель была не­верно специфицирована (проблема пропущенной переменной).

Несмотря на то, что в модели исправления ошибок используется оценка коинтегрирующего вектора, оценки коэффициентов, полученные из такой 44





модели будут иметь такие же асимптотические свойства, как если бы коин­тегрирующий вектор был точно известен. В частности, можно использовать t-статистики из этой регрессии, поскольку оценки стандартных ошибок яв­ляются состоятельными. Это является следствием сверхсостоятельности оценок коинтегрирующего вектора.

Коинтеграция в динамических системах: подход Йохансена

Другой популярный метод нахождения стационарных комбинаций метод Йохансена. Этот метод служит также для тестирования стационарности найденных линейных комбинаций, и по сути дела распространяет методику Дики-Фуллера на случай векторной авторегрессии ( то есть такой модели, в которой несколько зависимых переменных и зависят они от собственных лагов и от лагов других переменных). Если в обычной авторегрессии мы рассматривали один коэффициент р, то здесь следует рассматривать уже матрицу коэффициентов. Предполагается (как и в ADF), что если добавить достаточное число лагов в авторегрессионную модель, то ошибка не будет сериально коррелированной.

Если векторный процесс состоит более чем из двух процессов (S>2), то может существовать несколько коинтегрирующих векторов. Если существу­ет ровно r линейно независимых коинтегрирующих векторов, то говорят, что ранг коинтеграции равен r.

Обозначим /3 матрицу, составленную из таких векторов. Набор коинтег­рирующих векторов не является однозначным, на самом деле речь должна идти о коинтеграционном пространстве. Нормировку следует выбирать ис­ходя из экономической теории рассматриваемых процессов.

Метод Йохансена позволяет не только найти матрицу коинтеграционных векторов при данном ранге коинтеграции, но и проверять гипотезы о ранге коинтеграции (количестве коинтегрирующих векторов). Метод непосредст-

венно работает с векторной моделью исправления ошибок. Пусть Yt = (Y₁t,

... , Ynt) - векторный процесс (вектор-строка), каждая из компонент которого является 1(1) (или 1(0)). Порождающий данные процесс задается формулой

ЛУt= µ₀ + µ₁t + Уt_₁П + ЛУt_₁Г1 + ... + ЛYt-L+IГL-1 +& t·

Предполагается, что ошибки, относящиеся к разным моментам времени, независимы, и е t N(O,.Q). В модели оцениваются вектор-строка констант µ₀ и коэффициентов при трендах µ₁, матрицы коэффициентов Г₁, •.• , ГL-l и П 45



(пхп), а также ковариационная матрица Q. Поскольку по предположению ЛYtl(O), то должно быть выполнено Уt_₁П 1(0). Ограничения на ранг коин­теграции задаются как ограничения на матрицу П. При нулевой гипотезе, что ранг коинтеграции равен r, ее можно представить в виде

H₀(r): П = {За т,

где матрицы а и /3 имеют размерность (nxr); {З- матрица коинтегрирующих векторов, а - матрица корректирующих коэффициентов. Если r = О, то П = О

и не существует стационарных линейных комбинаций переменных Y₁t, ••• , Уп t" В другом крайнем случае, когда п = r любая линейная комбинация этих пе­ременных стационарна, то есть все они 1(0).

Для оценивания модели используется метод максимального правдопо­добия. При данной матрице fЗ можно получить оценки максимального прав­доподобия для остальных неизвестных параметров обычным методом наи­меньших квадратов. Йохансен показал также, что максимизация функции правдоподобия по fЗ эквивалентна задаче отыскания собственных чисел для некоторой симметричной положительно определенной матрицы. При ранге коинтеграции r выбираются r минимальных собственных чисел. Если распо­ложить собственные числа в порядке возрастания (л. ₁ :::; л.₂:::; ••• :::; Ап), то следует выбрать л.₁, л.₂, ... , А r· (Йохансен записал ПДП в несколько ином виде, и по­этому у него собственные числа идут в порядке убывания и выбираются r максимальных собственных чисел.) Столбцами матрицы fЗ (коинтегриру­ющими векторами) будут соответствующие собственные вектора. Конечно, /3 определяется только с точностью до некоторой нормировки. После того, как

найдена оценка максимального правдоподобия {з, вычисляются оценки дру­гих параметров.

Для проверки гипотез об r используется статистика отношения правдо­подобия. Статистика следа используется для проверки гипотезы (Но) о том, что ранг равен r, против гипотезы (Нь) о том, что ранг равен п. Статистика имеет вид


п

LRtrace = - т I ln(l - лi).

i=r+l

Тестирование проводится последовательно для r = п-1, ... ,0 и заканчива­ется, когда нулевая гипотеза не будет отвергнута в первый раз. Можно про­водить тестирование в обратном порядке r = О, ... , п-1. В этом случае тести- 46





рование заканчивается, когда нулевая гипотеза будет отвергнута в первый раз.

Можно также использовать статистику максимального собственного числа, которая используется для проверки гипотезы (Но) о том, что ранг ра­вен r, против гипотезы (Нл) о том, что ранг равен r + 1. Эта статистика равна LRл-max = - ln(l - л r-+-J).

Обе статистики имеют нестандартные асимптотические распределения.

К счастью, их распределения не зависят от мешающих параметров. Распре­деление этих статистик зависит только от п - r и от того, как входят в модель константа и тренд.

Можно выделить пять основных случаев, касающихся статуса векторов µ₀ и µ₁ в модели. В порядке перехода от частного к более общему:

Случай О. µ₀ = О, µ1 = О.

* т

Случаи 1 . µо = roa , µ1 = О.

Случай 1. µ₀ произвольный,

*

Случай 2 . µ₀ произвольный,

Случай 2. µ₀ произвольный, µ₁ произвольный.

Здесь ro и у₁ - вектора-строки длины r. Случай О легко понять - кон­станты и тренды в модели полностью отсутствуют. В Случае 1 константа входит в коинтеграционное пространство и, тем самым, в корректирующие механизмы, но не входит в сам процесс Yt в виде дрейфа. Это легко увидеть, если переписать модель следующим образом.

ЛУt= (ro + yt-L fЗ)а Т + ЛУr-1Г1 + ... + ЛYt-L+IГL-1 +& t·

т *

В Случае 1 µ₀ можно записать как µ₀ = у₀а + µ₀ , где у₀ входит в коинте-

*

грационное пространство, а µ₀ соответствует дрейфу в векторной модели

исправления ошибок. Дрейф в модели исправления ошибок означает, что в Yt входит линейный тренд. (См. выше рассмотрение простого авторегрессион­ного процесса с дрейфом.)

Аналогичные рассуждения верны по отношению ко временному тренду

* *

в Случаях 2 и 2. В Случае 2 тренд входит в коинтеграционное пространст-

во, но не входит в Yi в виде квадратичного тренда. В Случае 2 тренд входит и в коинтеграционное пространство, и в Yt в виде квадратичного тренда.





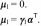
47


trace LR?c-max

етодом онте- арло получены та лицы и для всех пяти

случаев и нескольких значений n-r (на данный момент имеются таблицы для n-r= 1, ... ,12).

Как и в случае ADF очень важным вопросом является выбор длины лага L. Способы по сути дела являются теми же самыми. Для проверки гипотез о длине лага можно использовать тест отношения правдоподобия, который в данном случае имеет обычное распределение х²• Если процесс состоит из п компонент, и проверяется гипотеза о том, что следует увеличить L на едини­цу то количество степеней свободы соответствующей статистики равно п. Важно также, чтобы отсутствовала автокорреляция остатков.

Метод Йохансена можно использовать также для оценивания моделей с линейными ограничениями на матрицу коинтегрирующих векторов /3 и на матрицу корректирующих коэффициентов а. Для проверки таких ограниче­ний предлагается использовать все тот же тест отношения правдоподобия,

б 2

которыи здесь имеет о ычное асимптотическое распределение х .


48


<sub>м


ì


ê


б


L


R</sub>