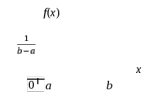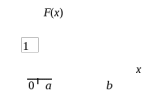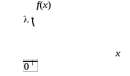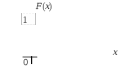шпоры к зачету по математике 2 курс 2 семестр. мат зачет. Зачёт Испытания и события. Пространство элементарных событий. Вероятность Р(А) есть числовая характеристика возможности появления события а в испытании.
 Скачать 4 Mb. Скачать 4 Mb.
|
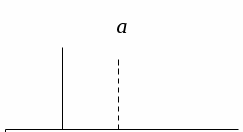
Свойства функции распределения и плотности вероятности1) Р(а Х < b) = F(b) – F(a). 2) Для непрерывной случайной величины Р(а Х < b)=  . Вероятность попадания случайной величины Х в интервал [a; b) равна площади криволинейной трапеции abBA (рис. 15). . Вероятность попадания случайной величины Х в интервал [a; b) равна площади криволинейной трапеции abBA (рис. 15).3) Для непрерывной случайной величины Р(х = а) = Р(х= b) = 0, следовательно, Р(а Х < b) = Р(а < Х < b)= Р(а Х b) = Р(а < Х b). 4) 5) 6) Числовые характеристики дискретной с.в: математическое ожидание и его свойства Математическое ожидание МХ – величина, около которой группируются возможные значения случайной величины Х (числовая характеристика положения). Для дискретной случайной величины: 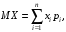 Для непрерывной случайной величины 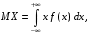 Размерность величины МХ совпадает с размерностью случайной величины Х Свойства: 1) М(С) = С (С – const). 2) М(С Х) = С МХ. 3) М(Х + Y) = МХ + МY. 4) М(ХY) = МХ МY, если X и Y независимы. Числовые характеристики дискретной с.в.: дисперсия и ее свойства ДисперсияDХ есть математическое ожидание квадрата отклонения случайной величины Х от ее математического ожидания: 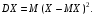 Дисперсия характеризует рассеяние (отклонение) случайной величины относительно её математического ожидания. Дисперсия характеризует рассеяние (отклонение) случайной величины относительно её математического ожидания. Для дискретной случайной величины 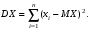 Размерность DХ равна квадрату размерности Х. Поэтому числовой характеристикой рассеяния является также среднее квадратическое отклонение Свойства: 5) D(С) = 0. 6) D(X) 0. 7) D(С Х ) = С 2DХ. 8) D(Х + Y) = DХ + DY, если X и Y независимы. 9) DХ = М(Х2) – (МХ)2. Законы распределения дискретной с.в.: биномиальный, Пуассона, геометрическое распределение. Числовые характеристики для этих законов. Биномиальное распределение имеет дискретная случайная величина Х, если она принимает целые значения от 0 до n, вероятности которых вычисляются по формуле Бернулли Р(Х = m) = Математическое ожидание и дисперия: МХ= np, DХ = npq. Распределение Пуассона с параметром > 0 имеет дискретная случайная величина Х, если она принимает целые неотрицательные значения, вероятности которых вычисляются по формуле Р(Х = m) = 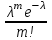 . .Математическое ожидание и дисперия: МХ= DХ = .  Плотность распределения непрерывной с.в. и ее связь с функцией распределения. Если функция F(х) дифференцируема, то ее производная f(х) = F’(х) называется плотностью распределения вероятностей. Плотность вероятности полностью характеризует непрерывную случайную величину. 7)f(х) 0. 8)f(х) = F(х) и F(х) = 9)  = 1. Площадь S, заключенная между графиком плотности распределенияf(х) и осью 0х, равна единице (рис. 15). = 1. Площадь S, заключенная между графиком плотности распределенияf(х) и осью 0х, равна единице (рис. 15).  Рис. 18 Функция распределения вероятностей: 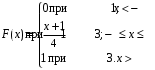 Плотность распределения вероятностей: 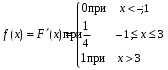 Числовые характеристики непрерывной с.в.: мат. ожидание, дисперсия. Математическое ожидание МХ – величина, около которой группируются возможные значения случайной величины Х (числовая характеристика положения). Дисперсия DХ есть математическое ожидание квадрата отклонения случайной величины Х от ее математического ожидания: 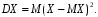 Дисперсия характеризует рассеяние (отклонение) случайной величины относительно её математического ожидания. Дисперсия характеризует рассеяние (отклонение) случайной величины относительно её математического ожидания.Для непрерывной случайной величины математическое ожидание и дисперсия вычисляются по формулам 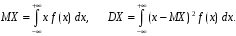 Законы распределения непрерывной с.в.: равномерный и показательный Равномерное распределение имеет непрерывная случайная величина Х, если ее плотность распределения вычисляется по формуле (рис. 19) 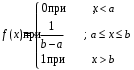 Функция распределения (рис. 20) Функция распределения (рис. 20)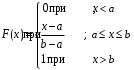
Рис. 19 Рис.20 Математическое ожидание и дисперия: МХ = 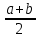 , DХ = , DХ = 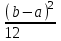 Вероятность попадания случайной величины X, распределенной по равномерному закону, в интервал (х1; х2) вычисляется по формуле Р(х1 < Х < х2) = 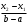 ; ; а х1 < x2 b. Показательное распределение с параметром > 0 имеет непрерывная случайная величина Х, если ее плотность распределения вычисляется по формуле (рис. 21) f(х) = 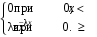
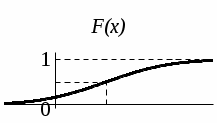
Рис. 21 Рис. 22 Функция распределения (рис. 22): 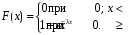 Вероятность попадания случайной величины X, распределенной по показательному закону, в интервал (х1; х2) вычисляется по формуле Р(х1 < Х < х2) = 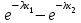 . .Математическое ожидание и дисперия: МХ = 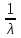 , DХ = , DХ = 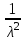 . .Законы распределения непрерывной с.в.: нормальный закон Нормальное распределение (N(а; ), закон Гаусса) с параметрами а и имеет непрерывная случайная величина Х, если ее плотность распределения вычисляется по формуле f(х) = 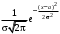 . .Функция распределения: F(х) = 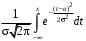 . .Математическое ожидание и дисперсия: МХ = а, DХ = 2.. На рисунках 23 и 24 изображены графики функций f(х) и F(х).
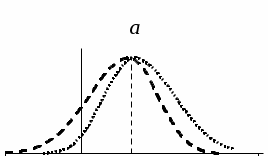
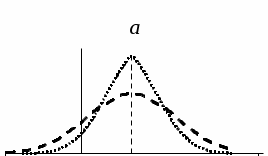
Рис. 23 Рис. 24 Функция Лапласа Ф0(t) (см. приложение В) позволяет записать функцию нормального распределения в виде 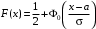 . .Вероятность попадания случайной величины X, распределенной по нормальному законуN(а; ), в интервал (х1; х2] вычисляется по формуле Р(х1 < Х х2) = 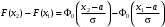 . .Для нормально распределенной случайной величины верна формула Вероятностный смысл параметров нормально распределенной с.в Математическое ожидание и дисперсия: МХ = а, DХ = 2.. (См. также пункт 20) Правило трех сигм. Правило «трех сигм». Для нормально распределенной случайной величины Х практически достоверно, что все ее значения попадают в интервал (а – 3; а + 3). Для распределений близких к нормальному используются также числовые характеристики: асимметрия 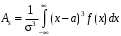 и эксцесс и эксцесс 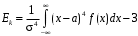 . Они сравнивают «скошенность» (рис. 25) и «островершинность» (рис. 26) графиков плотности изучаемого и нормального распределений. Для нормального закона распределения, график плотности которого изображен на рисунках сплошной линией, асимметрия и эксцесс равны нулю. . Они сравнивают «скошенность» (рис. 25) и «островершинность» (рис. 26) графиков плотности изучаемого и нормального распределений. Для нормального закона распределения, график плотности которого изображен на рисунках сплошной линией, асимметрия и эксцесс равны нулю.
Рис. 25 Рис. 26 Неравенство Чебышёва 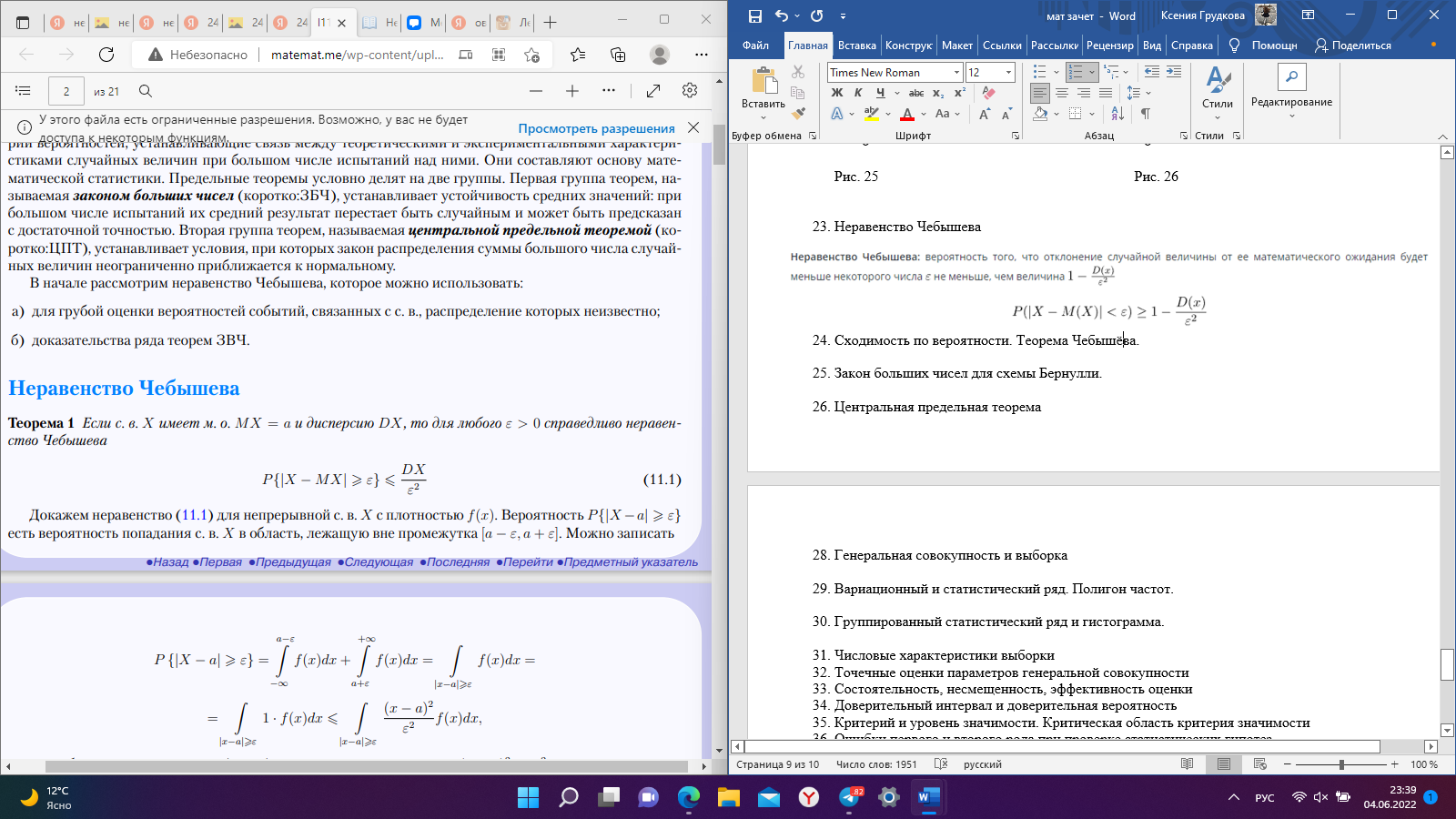 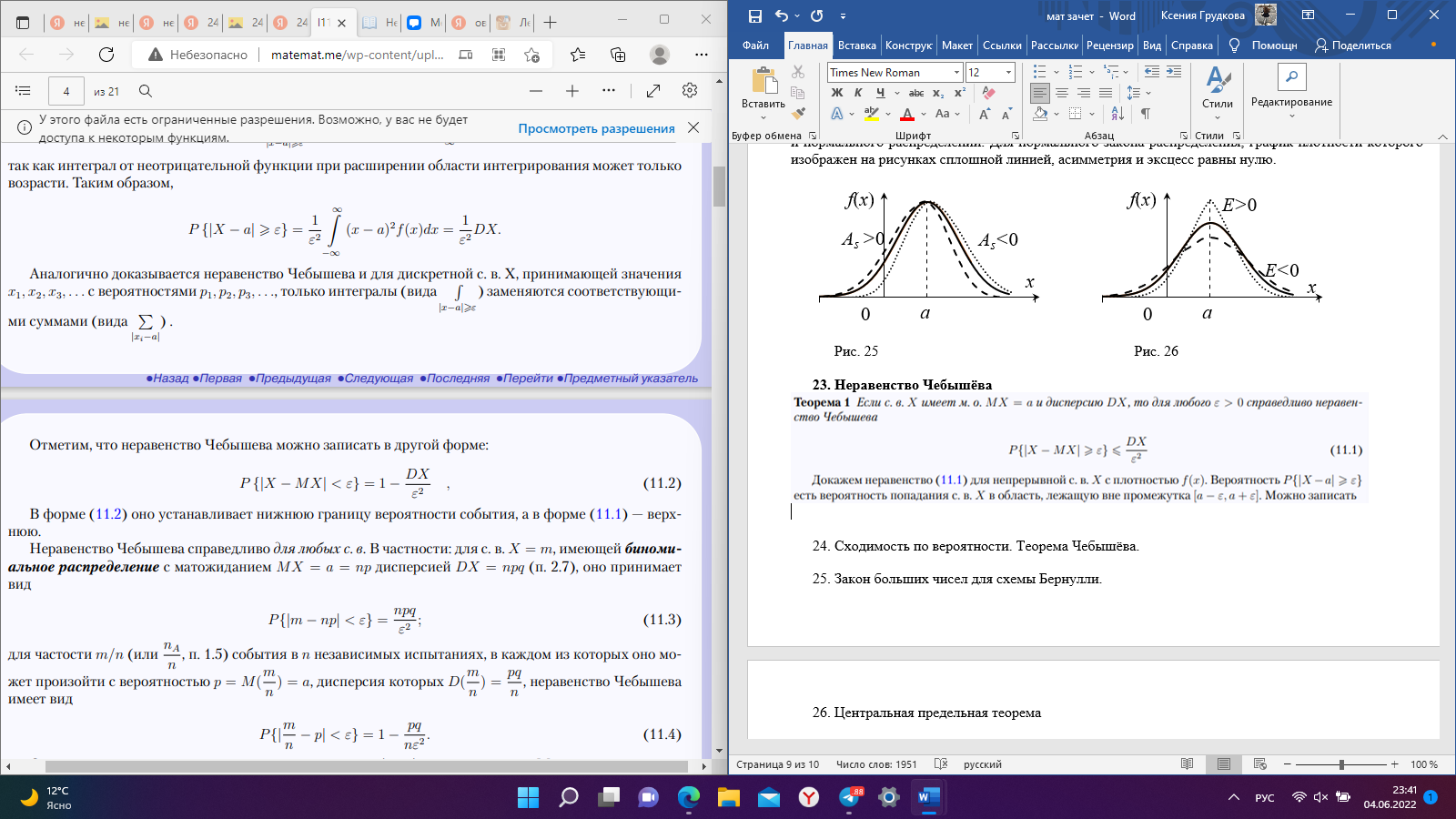 Сходимость по вероятности. Теорема Чебышёва. 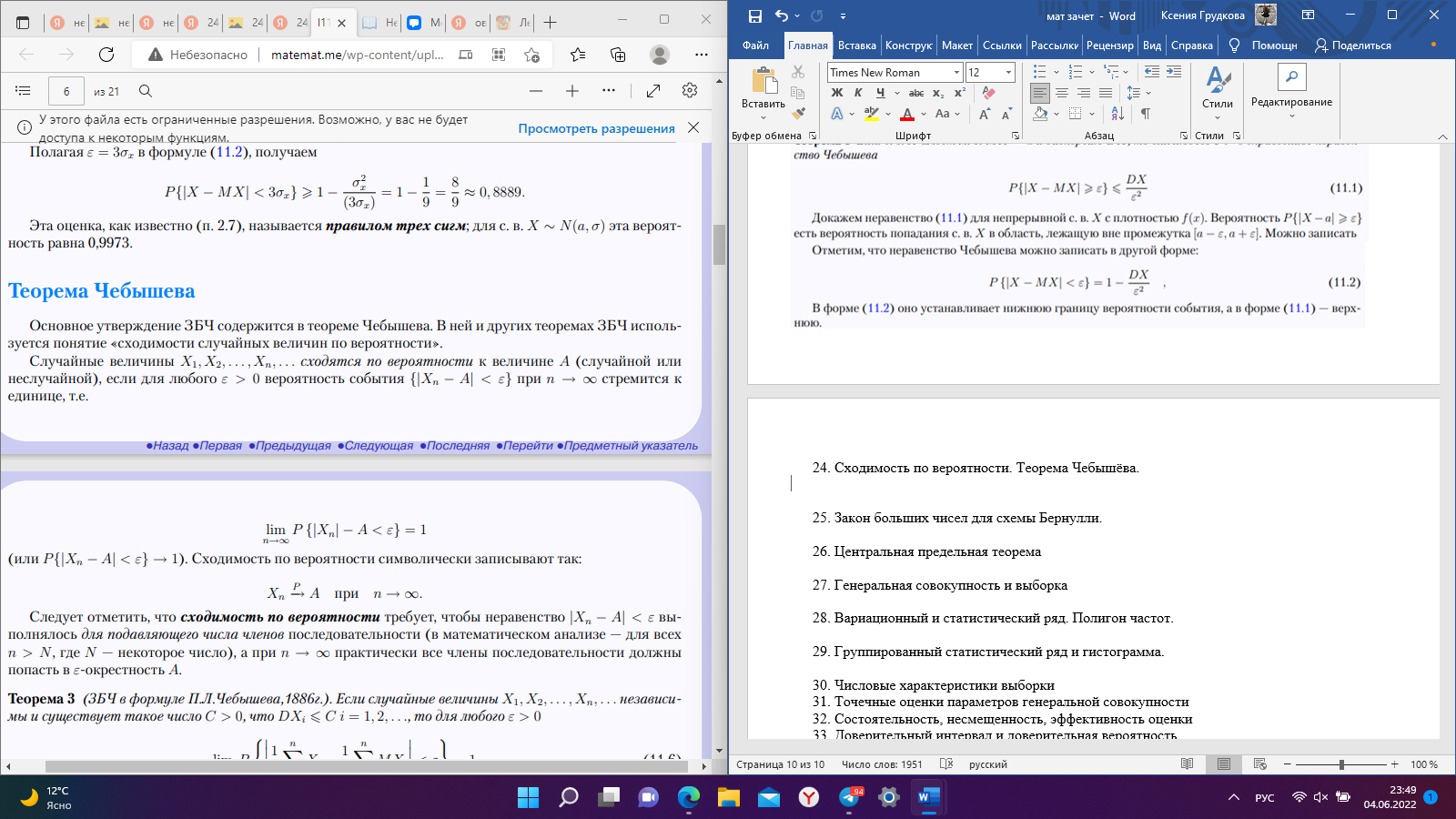 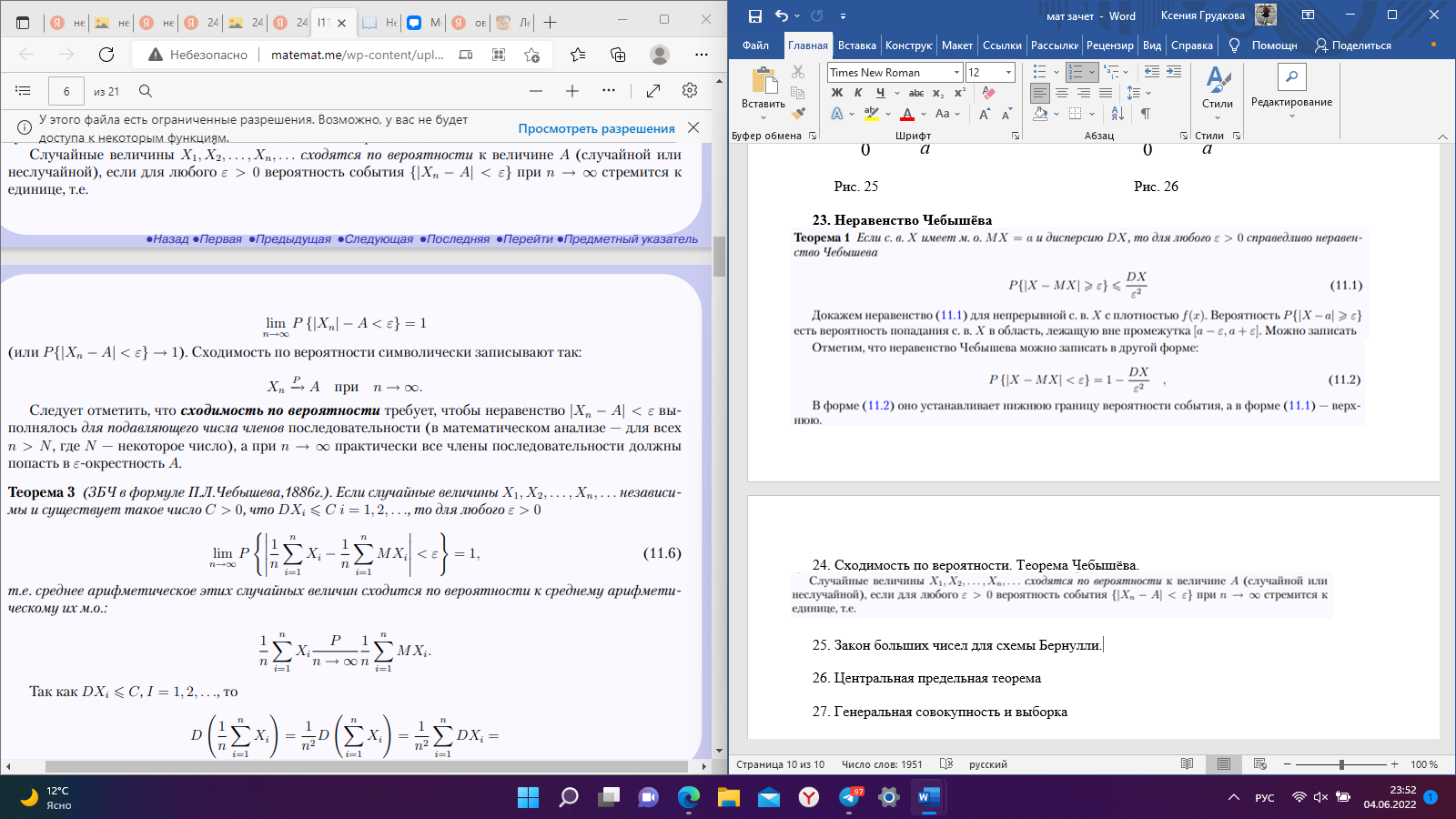 Закон больших чисел для схемы Бернулли. Закон больших чисел устанавливает устойчивость средних значений; при большом числе испытаний их средний результат перестает быть случайным и может быть предсказан с достаточной точностью. 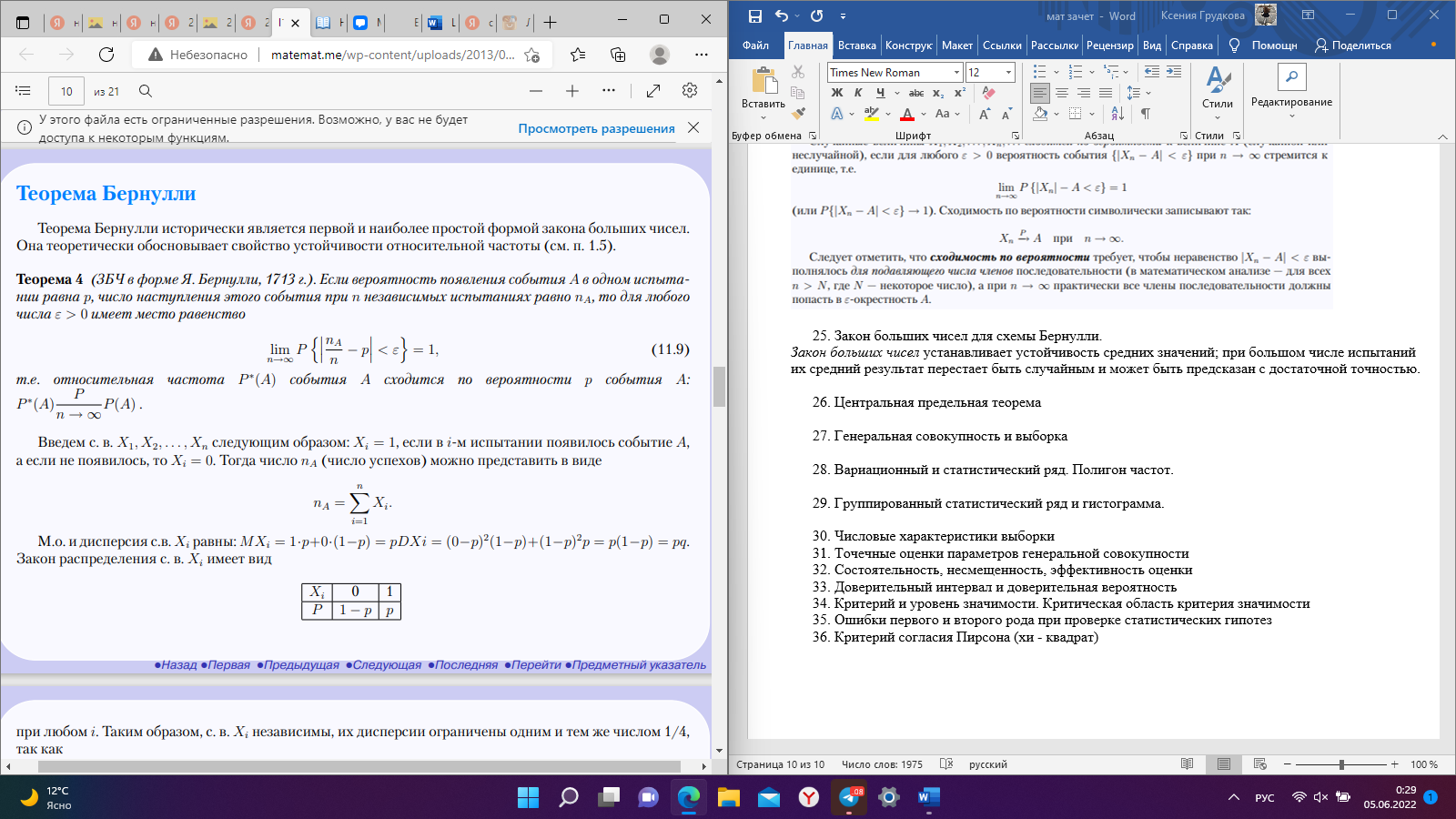 Центральная предельная теорема 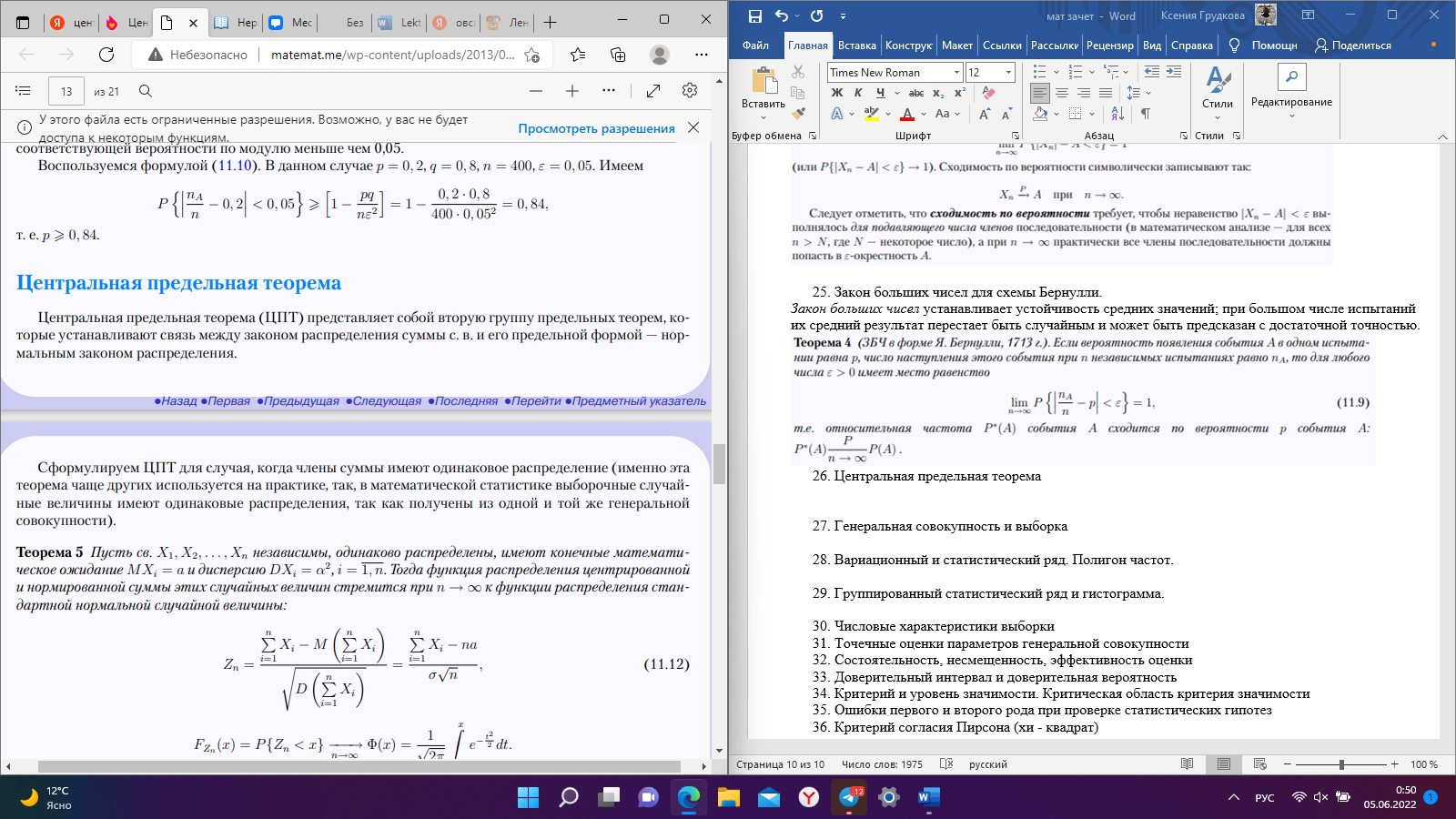  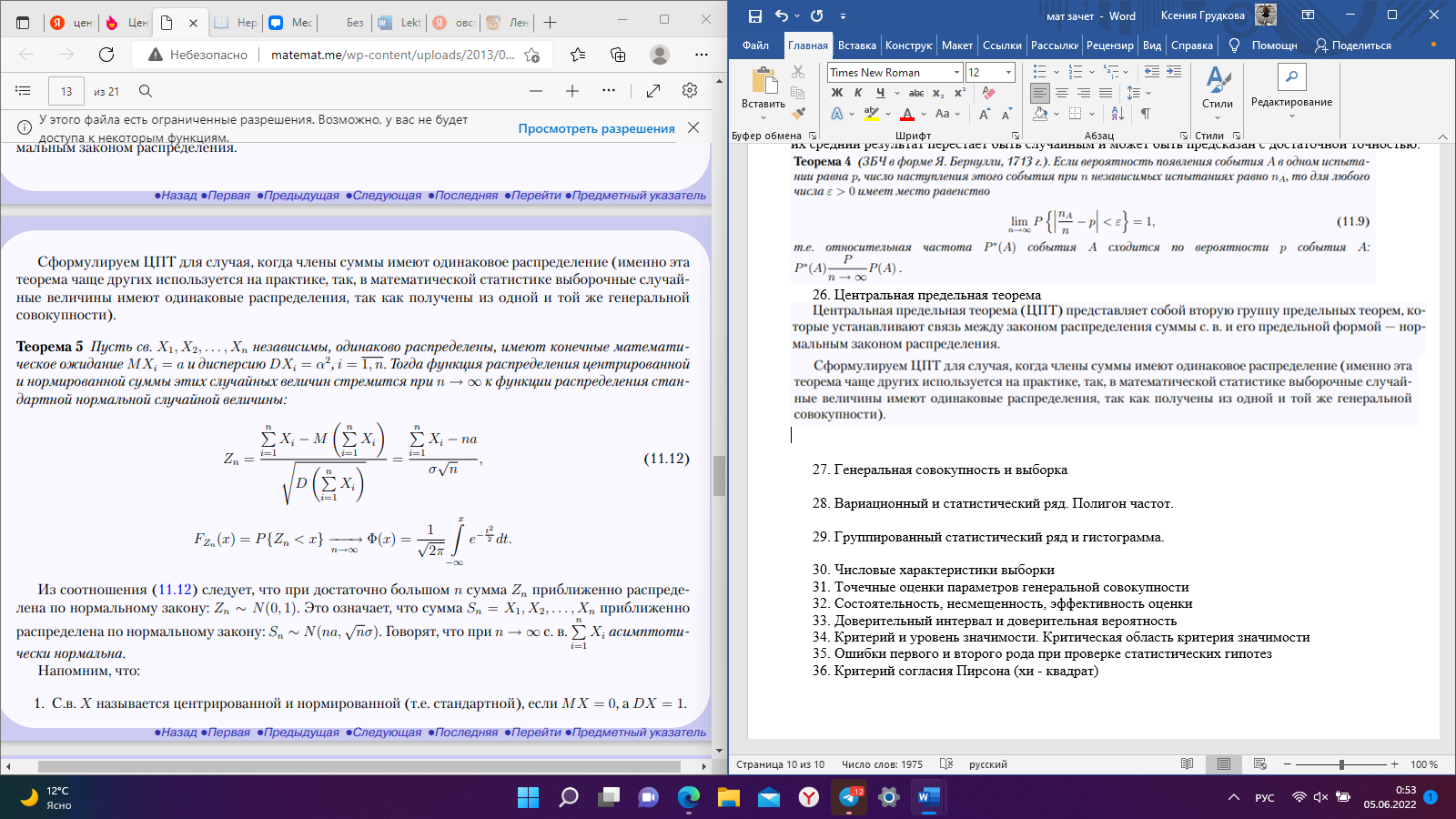 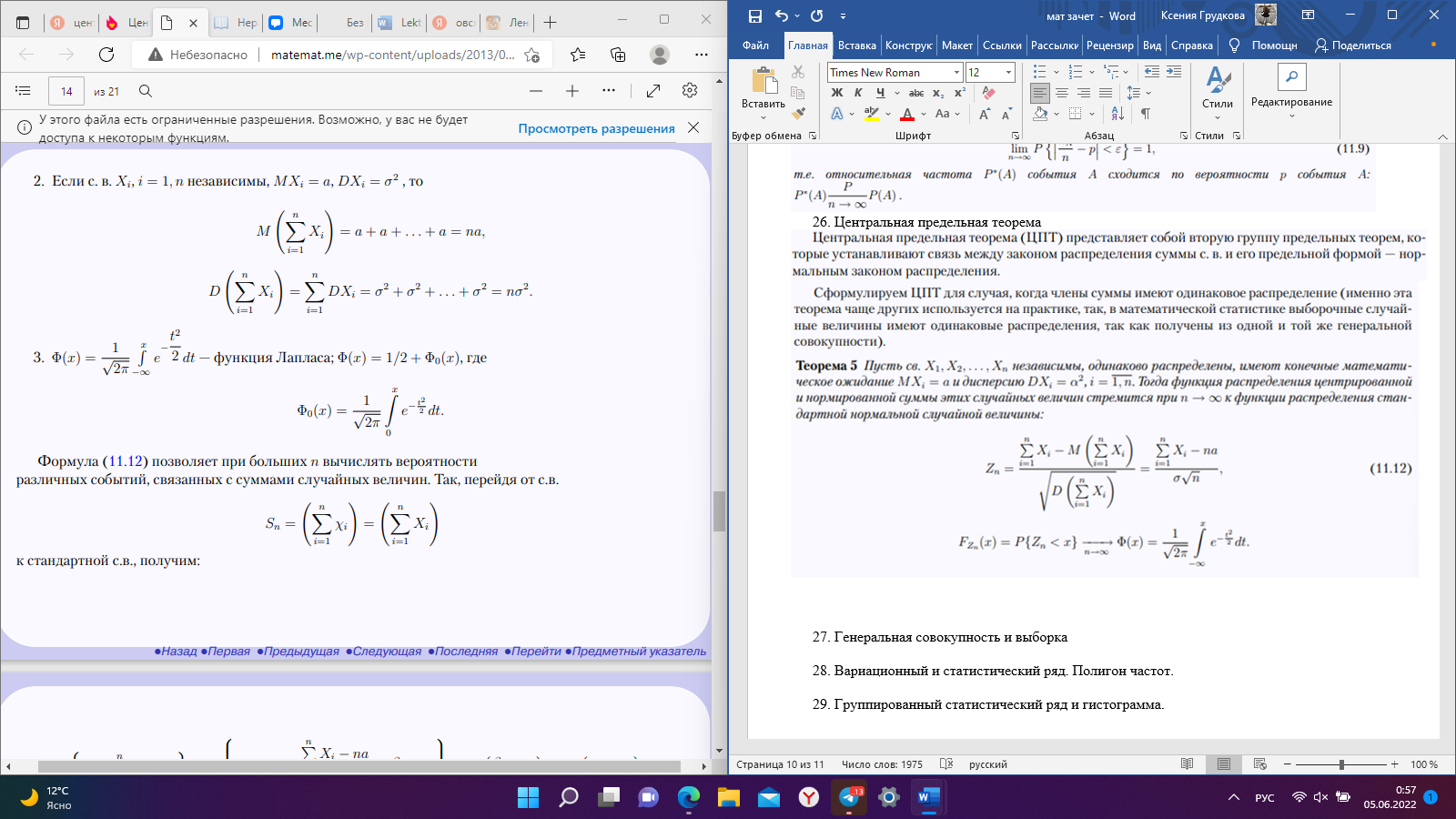 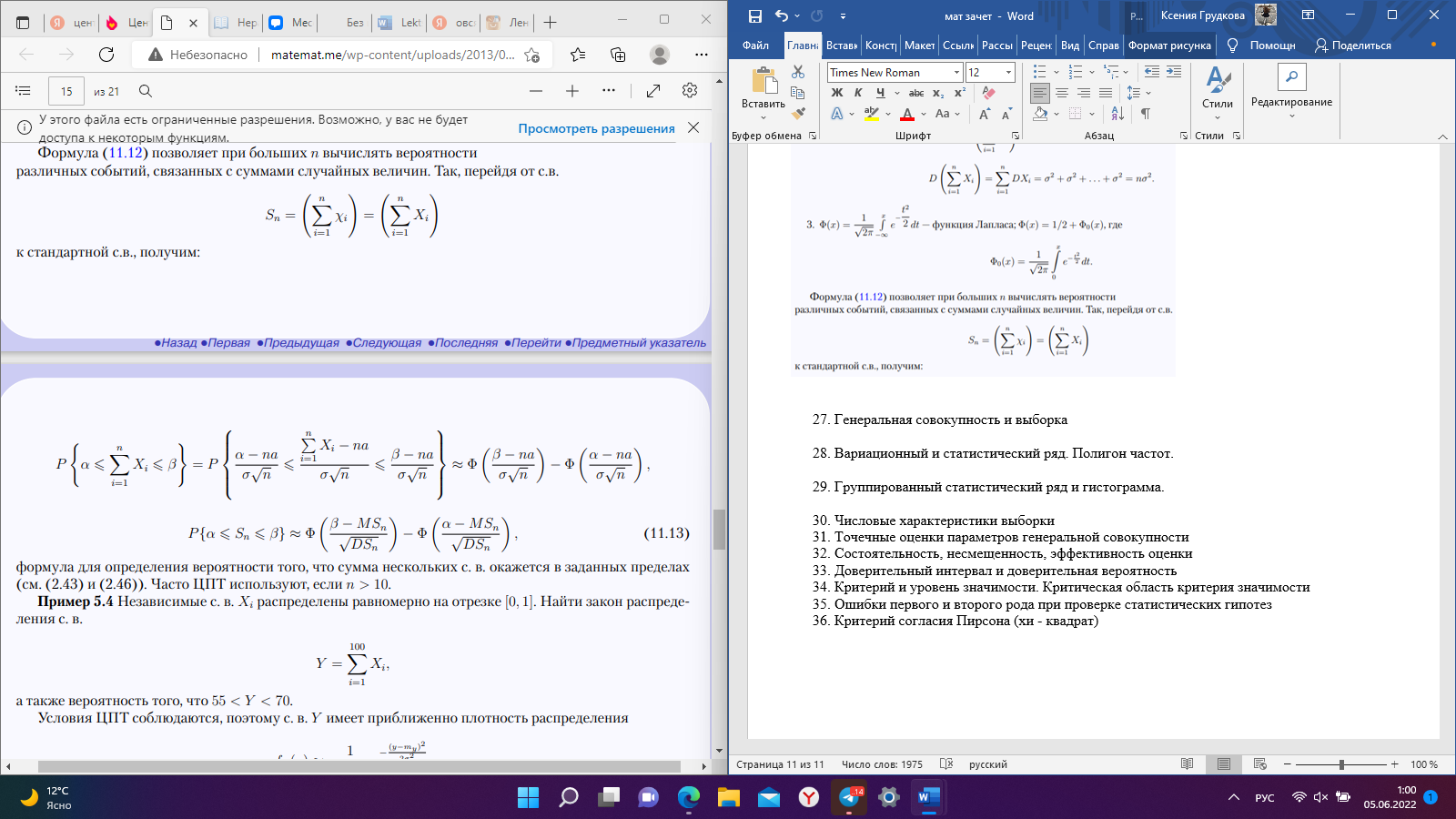 Генеральная совокупность и выборка Генеральной совокупностью Х называется множество изучаемых объектов, а также результаты наблюдений, характеризующие какое-нибудь свойство объекта. Выборкой называется случайно отобранный набор объектов множества Х или результаты Вариационный и статистический ряд. Полигон частот. Пусть из генеральной совокупности извлечена выборка, причем 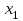 наблюдалось наблюдалось 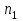 раз, раз, 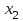 – – 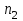 раз и т.д. При этом раз и т.д. При этом 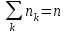 – объем выборки. Наблюдаемые значения – объем выборки. Наблюдаемые значения 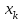 называют вариантами, а последовательность вариант, записанных в возрастающем порядке – вариационным рядом. Числа наблюдений называют вариантами, а последовательность вариант, записанных в возрастающем порядке – вариационным рядом. Числа наблюдений 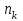 называются частотами, а их отношение к объему выборки называются частотами, а их отношение к объему выборки 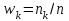 – относительными частотами. – относительными частотами.Статистическим распределением выборки (статистическим рядом) называется перечень вариант и соответствующих им частот, который обычно оформляется в виде таблиц 1 или 2. Таблица 1 Таблица 2
Сумма всех чисел второй строки таблицы 2 равна единице: 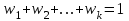 . Графическое представление статистического ряда в виде ломаной линии (рис. 1) называется полигоном частот. . Графическое представление статистического ряда в виде ломаной линии (рис. 1) называется полигоном частот. 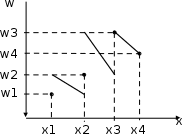 Рис. 1 |