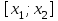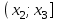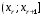шпоры к зачету по математике 2 курс 2 семестр. мат зачет. Зачёт Испытания и события. Пространство элементарных событий. Вероятность Р(А) есть числовая характеристика возможности появления события а в испытании.
 Скачать 4 Mb. Скачать 4 Mb.
|
|
Группированный статистический ряд и гистограмма. При большом количестве столбцов в таблице 1 составляется группированный статистический ряд (таблица 3), где Таблица 3
Аналогом графика плотности распределения случайной величины в математической статистике является гистограмма. Построенная таблица группированного ряда дополняется тремя строками (таблица 5): длина интервала Таблица 5
Гистограмма представляет собой набор прямоугольников высоты 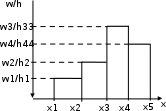 Рис. 4 Площадь каждого прямоугольника совпадает с соответствующей относительной частотой wj (или частотой nj при высотах Числовые характеристики выборки Выборочным средним  При заданном статистическом распределении выборки (см. табл. 1, 3) формула принимает вид 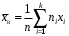 или или 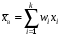 . .Выборочная медиана  Выборочная мода Выборочной дисперсией 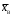 . .  При наличии статистического или группированного статистического рядов выборки (см. таблицы 1 и 3) формула принимает вид  или или 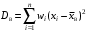 . .Выборочным средним квадратическим отклонением 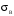 называется квадратный корень из выборочной дисперсии, т.е. называется квадратный корень из выборочной дисперсии, т.е. 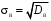 . . Величина  , называется исправленной выборочной дисперсией, а s – исправленным выборочным средним квадратическим отклонением. Характеристики рассеяния , называется исправленной выборочной дисперсией, а s – исправленным выборочным средним квадратическим отклонением. Характеристики рассеяния 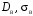 , s определяют величину разброса вариант относительно , s определяют величину разброса вариант относительно 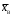 . . Свойства числовых характеристик выборки: 1) если все значения 2) если все значения 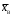 и и 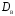 умножатся на с и с2 соответственно. умножатся на с и с2 соответственно. Точечные оценки параметров генеральной совокупности Точечной оценкой * (оценкой одним числом) неизвестного параметра генеральной совокупности является число, зависящее от элементов выборки. Точечная оценка, как функция от выборки, является случайной величиной и меняется от выборки к выборке при повторном эксперименте. К точечным оценкам предъявляют требования, которым они должны удовлетворять, чтобы хоть в каком-то смысле быть «доброкачественными». Это несмещённость, эффективность и состоятельность. В качестве оценок математического ожидания МХ, медианы 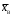 и соответствующие выборочные параметры и соответствующие выборочные параметры (см. п. 30) Мода М0 дискретной случайной величины – любое её значение, имеющее большую относительно двух соседних величин вероятность. Модой М0 непрерывной случайной величины называются точки максимума ее плотности распределения (рис. 17). Случайная величина может иметь несколько мод. 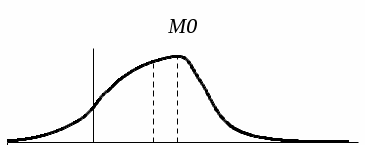 Рис. 17 Медианой непрерывной случайной величины Х называется ее значение Ме, при котором P(X < Ме) = P(X Ме) = 0,5 (рис 17), т.е. вертикальная прямая х = Ме, делит площадь, ограниченную кривой плотности распределения и осью х, на две равновеликие части. Состоятельность, несмещенность, эффективность оценки Для того чтобы статистические оценки давали “хорошие” приближения оцениваемых параметров, они должны удовлетворять определенным требованиям. Несмещённой – если ее мат. ожидание равно оцениваемому параметру при любом объеме выборки: 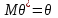 . То есть математическое ожидание оценки равно оцениваемому параметру. . То есть математическое ожидание оценки равно оцениваемому параметру.Эффективной - Статистическую оценку 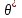 называют эффективной, если при заданном объеме выборки n оценка имеет наименьшую возможную дисперсию. называют эффективной, если при заданном объеме выборки n оценка имеет наименьшую возможную дисперсию.Состоятельной - Статистическую оценку 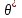 называют состоятельной, если для любого называют состоятельной, если для любого 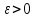 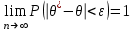 . .Доверительный интервал и доверительная вероятность Интервальной оценкой оцениваемого параметра генеральной совокупности называется интервал (* – ; * + ), накрывающий истинное значение параметра с заданной вероятностью , которая называется доверительной вероятностью P(*– < < *+ ) = . Интервал (* – ; * + ) называется доверительным интервалом (рис. 5), – точностью оценки.  Если при построении интервальных оценок математического ожидания и среднего квадратического отклонения предполагается, что генеральная совокупность Х распределена по нормальному закону с параметрами a и , то доверительные интервалы находятся по формулам  и и  . Значения t, удовлетворяющие уравнению . Значения t, удовлетворяющие уравнению При увеличении объема выборки n доверительный интервал уменьшается. Увеличение доверительной вероятности ведет к росту значения t (см. приложение В), т.е. увеличению доверительного интервала. Критерий и уровень значимости. Критическая область критерия значимости Статистической гипотезой называется гипотеза о неизвестном распределении или о параметрах неизвестного распределения. Нулевой или основной называется выдвинутая гипотеза H0. Конкурирующей или альтернативной называется гипотеза H1, которая противоречит нулевой. Статистический критерий – это некое правило, согласно которому нулевую гипотезу нужно принять или отвергнуть. Мы можем принять верную гипотезу Н0 или отвергнуть не верную гипотезу Н0 на основе критерия. В этом случае мы не совершаем никакой ошибки. А еще мы можем отвергнуть верную нулевую гипотезу – это называется ошибкой первого рода. (Отвергается правильная гипотеза) Для оценки возможности совершения такой ошибки используют вероятность, обозначаемую α и называемую уровнем значимости критерия. Уровень значимости должен стремиться к нулю. Следует принять решение относительно значения а прежде, чем будут собраны данные; обычно назначают условное значение 0,05 Критической областью называется область значений статистики критерия, при которых отвергается H0. А критические значения — это граница критической области. Существует три вида критических областей: левосторонняя, правосторонняя и двусторонняя. 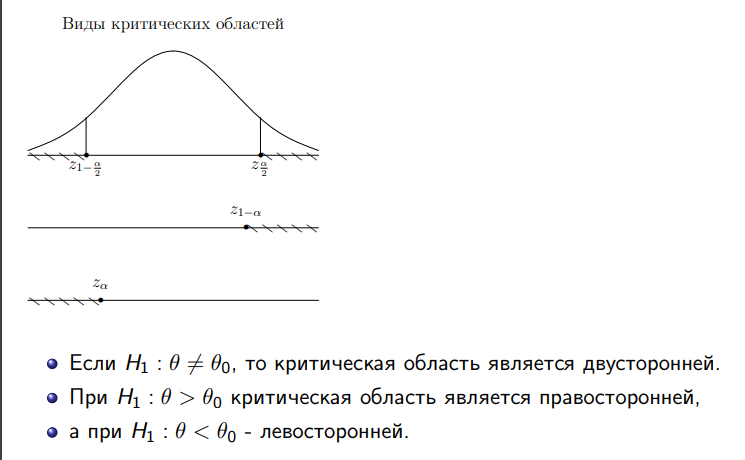 1) Критическая область, определяемая неравенством 1) Критическая область, определяемая неравенством 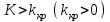 называется правосторонней. называется правосторонней.2) Критическая область, определяемая неравенством 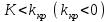 называется левосторонней. называется левосторонней.Двусторонняя область определяется неравенствами 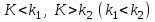 . Часто критические точки k1 и k2 симметричны относительно нуля, поэтому критическая область определяется неравенством . Часто критические точки k1 и k2 симметричны относительно нуля, поэтому критическая область определяется неравенством 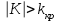 . .Проверка статистических гипотез осуществляется следующим образом: 1. по выборке вычисляется наблюдаемое значение критерия (Кнабл). 2. если Кнабл попало в критическую область нулевую гипотезу отвергают, а если в область принятия гипотезы H0 принимают. |