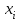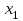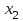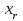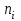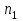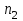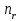шпоры к зачету по математике 2 курс 2 семестр. мат зачет. Зачёт Испытания и события. Пространство элементарных событий. Вероятность Р(А) есть числовая характеристика возможности появления события а в испытании.
 Скачать 4 Mb. Скачать 4 Mb.
|
|
Ошибки первого и второго рода при проверке статистических гипотез Выдвинутая гипотеза может быть правильной или неправильной, поэтому возникает необходимость в ее проверке. Поскольку проверку производят статистическими методами, то ее называют статистической. В результате статистической проверки гипотезы могут быть допущены ошибки двух типов: Отвергается правильная гипотеза. Эта ошибка называется ошибкой первого рода. Максимальный шанс (вероятность) допустить ошибку 1-го рода обозначается α (альфа). Это уровень значимости критерия; нулевую гипотезу отвергают, если наше значение p ниже уровня значимости, т. е., если p < α. Следует принять решение относительно значения а прежде, чем будут собраны данные; обычно назначают условное значение 0,05, хотя можно выбрать более ограничивающее значение, например 0,01. Шанс допустить ошибку 1-го рода никогда не превысит выбранного уровня значимости, скажем α = 0,05, так как нулевую гипотезу отвергают только тогда, когда p< 0,05. Если обнаружено, что p > 0,05, то нулевую гипотезу не отвергнут и, следовательно, не допустят ошибки 1-го рода. Принимается неправильная гипотеза. Эта ошибка называется ошибкой второго рода. Шанс возникновения ошибки 2-го рода обозначается β (бета); а величина (1-β) называется мощностью критерия. Следовательно, мощность — это вероятность отклонения нулевой гипотезы, когда она ложна. В идеале хотелось бы, чтобы мощность критерия составляла 100%; однако это невозможно, так как всегда остается шанс, хотя и незначительный, допустить ошибку 2-го рода. Критерий согласия Пирсона (хи - квадрат) Критерием согласия называют критерий проверки гипотезы о предполагаемом законе неизвестного распределения. Пусть по выборке объема n получено эмпирическое распределение:
Допустим, что в предположении о нормальном распределении генеральной совокупности вычислены теоретические частоты 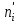 . При уровне значимости . При уровне значимости 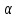 требуется проверить нулевую гипотезу: генеральная совокупность распределена нормально. В качестве критерия проверки этой гипотезы возьмем случайную величину требуется проверить нулевую гипотезу: генеральная совокупность распределена нормально. В качестве критерия проверки этой гипотезы возьмем случайную величину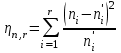 Ясно, что чем меньше различаются эмпирические и теоретические частоты, тем меньше величина критерия (4). Возведение в квадрат разностей частот устраняет возможность взаимного погашения положительных и отрицательных слагаемых в (4). Делением на 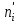 достигают уменьшения каждого из слагаемых. Без этого сумма (4) была бы настолько велика, что приводила бы к отклонению нулевой гипотезы даже и тогда, когда она справедлива. достигают уменьшения каждого из слагаемых. Без этого сумма (4) была бы настолько велика, что приводила бы к отклонению нулевой гипотезы даже и тогда, когда она справедлива.Можно доказать, что при 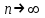 закон распределения критерия (4) независимо от того, по какому закону распределена генеральная совокупность, стремится к закону распределения закон распределения критерия (4) независимо от того, по какому закону распределена генеральная совокупность, стремится к закону распределения 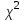 с k степенями свободы. Поэтому критерий (4) называют критерием согласия хи-квадрат (критерием Пирсона). Число степеней свободы определяется равенством с k степенями свободы. Поэтому критерий (4) называют критерием согласия хи-квадрат (критерием Пирсона). Число степеней свободы определяется равенством 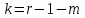 , где r – число групп выборки; m – число параметров предполагаемого распределения, которые оценены по данным выборки. Так, если предполагаемое распределение нормальное, то оценивают два параметра ( , где r – число групп выборки; m – число параметров предполагаемого распределения, которые оценены по данным выборки. Так, если предполагаемое распределение нормальное, то оценивают два параметра (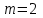 ) и тогда число степеней свободы: ) и тогда число степеней свободы: 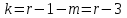 . .Построим правостороннюю критическую область, исходя из заданного значения уровня значимости 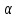 : :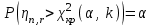 . .Обозначим значение критерия, вычисленное по данным наблюдений, через 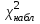 . Тогда правило проверки нулевой гипотезы формулируется следующим образом: . Тогда правило проверки нулевой гипотезы формулируется следующим образом:1) вычисляются теоретические частоты 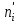 и по ним находится и по ним находится 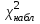 (формула 4); (формула 4);2) по таблице критических точек распределения хи-квадрат, по заданному уровню значимости 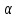 и числу степеней свободы и числу степеней свободы 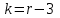 находится критическая точка находится критическая точка 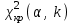 ; ;3) сравниваются 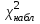 и и 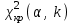 : :а) если 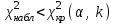 , то нет оснований отвергнуть нулевую гипотезу (гипотеза принимается); , то нет оснований отвергнуть нулевую гипотезу (гипотеза принимается);б) если 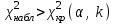 , то гипотеза отвергается. , то гипотеза отвергается.Замечание. Объем выборки должен быть достаточно велик, во всяком случае, не менее 50. Каждая группа должна содержать не менее 5-8 вариант. Малочисленные группы нужно объединить в одну, суммируя частоты. |