Контрольная работа по предмету. Задача в пространстве 3х товаров рассмотрите бюджетное множество при векторе цен p и доходе q
 Скачать 108.69 Kb. Скачать 108.69 Kb.
|
 Контрольная работа по предмету «Экономико-математические модели» Контрольная работа по предмету «Экономико-математические модели»Задача № 1. В пространстве 3-х товаров рассмотрите бюджетное множество при векторе цен P и доходе Q.
Задача № 2. Пусть производственная функция есть функция Кобба – Дугласа. Чтобы увеличить выпуск продукции на α %, надо увеличить основные фонды на b % или численность работников на с %. В настоящее время 1 работник за месяц производит продукции на М руб., а всего работников L. Основные фонды оцениваются в К руб. В ответе дайте:
Задача № 3. Даны зависимости спроса D и предложения S от цены. Найдите:
Цену, при которой выручка максимальна и эту максимальную выручку
Образец решения Задача № 1. В пространстве 3-х товаров рассмотрите бюджетное множество при векторе цен P и доходе Q.
Данные: P=(3, 8, 5); Q=120. Решение. Вектор цен: P=(3, 8, 5); Набор товаров Х=(х1, х2, х3) (набор товаров – это вектор – столбец, но по соображениям экономии записываем его в виде вектора - строки); Бюджетное множество В – это множество всех наборов товаров Х, которое потребитель может купить на данное количество денег Q при данных ценах Р (при этом необязательно тратить все деньги).
Обычными: Векторными: Общий вид: р1х1+р2х2+р3х3 ≤ Q Р*Х ≤ Q х1, х2, х3 ≥ 0 Х ≥ 0 В нашем случае: 3х1+8х2+5х3 ≤ 120 х1, х2, х3 ≥ 0 Граница бюджетного множества – это его часть, это множество всех наборов товаров стоимостью Q. Границу бюджетного множества можно описать равенствами: Обычными: Векторными: Общий вид: р1х1+р2х2+р3х3 = Q Р*Х = Q х1, х2, х3 ≥ 0 Х ≥ 0 В нашем случае: 3х1+8х2+5х3 = 120 х1, х2, х3 ≥ 0
Q/р1 = 120/3 = 40 Q/р2 = 120/8 = 15 Q/р3 = 120/5 = 24 
Ответ: 2400 Задача № 2. Пусть производственная функция есть функция Кобба – Дугласа. Чтобы увеличить выпуск продукции на α %, надо увеличить основные фонды на b % или численность работников на с %. В настоящее время 1 работник за месяц производит продукции на М руб., а всего работников L. Основные фонды оцениваются в К руб. В ответе дайте:
Данные: а=2, b=4, с=6, М=104, L=103,К=1011. Решение. Производственная функция Кобба – Дугласа имеет вид Y = A * Kα*Lβ, где А, α, β – константы (А, α, β > 0, α + β < 1); К – объем фондов либо в стоимостном выражении, либо в натуральном количестве. L – объем трудовых ресурсов – число рабочих, число человеко-дней и т. д. Y – выпуск продукции в стоимостном или натуральном выражении. При этом β – эластичность продукции по труду, α - эластичность продукции по фондам. Средняя фондоотдача к = Y/К – отношение объема произведенного продукта к величине фондов. α = а/b = 2/4 = ½, β = а/с = 2/6 = 1/3 , следовательно Y = A * K1/2*L1/3 Для нахождения А подставим в эту формулу К, L, М, учитывая, что Y= М L Y =104 * 103 = A * (1011)1/2*(103)1/3 А = 3,2 Найдем среднюю фондоотдачу к = Y/К = 107/1011=0,0001 Ответ: Производственная функция: Y = A * K1/2*L1/3 Средняя фондоотдача к = 0,0001 Задача № 3. Даны зависимости спроса D и предложения S от цены. Найдите:
Данные: D=200-10*p S=35 + 5*p. Решение Точка равновесия характеризуется равенством спроса и предложения, 200-10*p = 35 + 5*p р’ = 11. Выручка при равновесной цене W = p’D(p’) = 11*(200-10*11) = 990. В общем же случае при цене р выручка W(p) = p(min(D(p), S(p))). На рисунке показан график выручки в зависимости от цены.  Максимум W достигается при р = 10 и равен 1000. Таким образом, максимум достигается не при равновесной цене. Ответ: р’ = 11, W = 990, рmax = 10, Wmax = 1000 Задания № 4. Пусть все народное хозяйство (район и т.д.) состоит из трех отраслей, каждая из которых выпускает один вид из продукции. В таблице 4 указаны расходные коэффициенты (прямые затраты) aik единиц продукции i-ой отрасли, используемые как сырье (промежуточный продукт) для выпуска единицы продукции k-й отрасли, а также количество единиц yi продукции i-й отрасли, предназначенные для реализации (конечный продукт). Пусть дополнительно заданы расходные нормы двух видов сырья и топлива на единицу продукции соответствующей отрасли, трудоемкость продукции в человеко-часах на единицу продукции, стоимость единицы соответствующего материала и оплата за 1 чел. (таблица 5). Определить: 1.Коэффициенты полных затрат. 2.Валовой выпуск для каждой отрасли. 3. Производственную программу отраслей. 4. Коэффициенты косвенных затрат. 5. Суммарный расход сырья, топлива и трудовых ресурсов на выполнение производственной программы. 6. Коэффициенты прямых затрат сырья, топлива и труда на единицу конечной продукции каждой отрасли. 7.Расход сырья, топлива и трудовых ресурсов по отраслям. 8. Производственные затраты в денежных единицах по отраслям и на всю производственную программу. 9. Производственные затраты на единицу конечной продукции. 10. Параметры агрегирования при объединении первой и третьей отраслей. Вариант 1.
Вариант 2.
Вариант 3.
Вариант 4.
Вариант 5.
Вариант 6.
Вариант 7.
Вариант 8.
Вариант 9.
Вариант 10.
Пример решения задачи № 4
Решение.
X-AX=Y, где AX – внутрипроизводственное потребление. (E-A)X=Y X=(E-A)-1Y (E-A)-1= 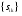 - матрица, обратная для (Е-А), представляет собой искомые коэффициенты полных внутрипроизводственных затрат. - матрица, обратная для (Е-А), представляет собой искомые коэффициенты полных внутрипроизводственных затрат.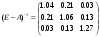 Таким образом, например, для выпуска единицы продукции 1, 2, 3 отраслей необходимо затратить продукции 1-ой отрасли соответственно 1,04, 0,21. 0,03 единиц.
 Следовательно, х1 = 238, х2 =187, х3=400.
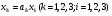 И представить в виде таблицы: Таблица 6
 5.Суммарный расход сырья А, сырья В, топлива и труда можно получить, умножив матрицу нормы расхода на валовой продукт: 
 Таким образом, например, для изготовления y1=1 необходимо затратить 1,98 единиц сырья А, 0,17 единиц сырья В, 2,52 единиц топлива и 15,2 человеко-часов.
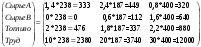 8.Производственные расходы по отраслям можно получить путем умножения слева строки стоимостей (5, 12, 2, 1,2) на матрицу п.7:  9.Производственные затраты на единицу конечной продукции, необходимые для определения себестоимости продукции, можем найти путем умножения слева матрицы полных затрат, найденном в п. 6 на строку цен: 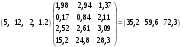 Таким образом, внутрипроизводственные затраты на единицу товарной продукции 1, 2, 3 отраслей соответственно равны: 35.2, 59.6, 72.3. 10. Выделим в таблице отрасли, подлежащие агрегированию. Присвоим новой отрасли индекс k. Матрица коэффициентов прямых затрат с учетом агрегирования определяется формулой Аагр=TAW*, Где матрицы Т получается из единичной матрицы с помощью горизонтальной деформации:  Матрица W получается из единичной матрицы с весовыми коэффициентами с помощью деформации по столбам: 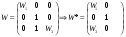  , , 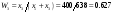  Новая производственная программа имеет вид: Таблица 7
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

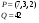





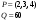

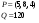


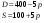





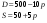

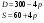
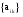 расходные коэффициенты (таблица 1), тогда производственные взаимосвязи могут быть представлены формулой
расходные коэффициенты (таблица 1), тогда производственные взаимосвязи могут быть представлены формулой