Контрольная работа Финансы. КР КрасГАУ Финансы вар 6. Задача 1 14 Задача 2 14 Задача 3 15 Список использованных источников 17 Введение

• Название: Задача 1 14 Задача 2 14 Задача 3 15 Список использованных источников 17 Введение
• Анкор: Контрольная работа Финансы
• Дата: 03.10.2020
• Размер: 173 Kb.
• Имя файла: КР КрасГАУ Финансы вар 6.doc
• Тип: Задача; #140749

СОДЕРЖАНИЕ

Введение 3

1 Конверсия финансовых рент. Замена ренты с одними условиями на ренту с другими условиями 5

2 Практические задания 14

Задача 1 14

Задача 2 14

Задача 3 15

Список использованных источников 17

Введение

В большинстве коммерческих операций вместо разовых платежей встречается последовательность денежных поступлений или выплат. Серия потоков поступлений или выплат называется потоком платежей. Поток однонаправленных платежей с равными интервалами времени между последовательными платежами в течение определенного количества лет представляет собой аннуитет (финансовая рента).

Часто аннуитетом называют финансовый актив, приносящий фиксированный доход ежегодно в течение ряда лет [7, с.28].

В буквальном переводе "аннуитет" подразумевает, что платежи происходят с интервалом в один год, однако встречаются потоки с иной периодичностью выплат.

Очевидно, что рента - это более широкое понятие, чем аннуитет, так как существует множество денежных потоков, члены которых не равны друг другу или распределены неравномерно [7, с.28].

Форму аннуитетов имеют многие финансовые потоки, например выплата доходов по облигациям или платежи по кредиту, страховые взносы. Можно сказать, что финансы тяготеют к упорядочению денежных потоков.

Принцип временной ценности денег делает невозможным прямое суммирование членов ренты. Для учета влияния фактора времени к каждому члену ренты применяются рассмотренные выше правила наращения и дисконтирования только сложных процентов, то есть предполагается, что получатель потока имеет возможность реинвестировать получаемые им суммы.

Если бы размеры рент всегда ограничивались двумя-тремя членами, то необходимость создания специальных способов расчета денежных потоков, возможно, и не возникла.

Ни в теории, ни на практике таких ограничений нет, наоборот, существуют большие, очень большие и даже бесконечные денежные потоки (вечные ренты), поэтому были разработаны специальные методы, позволяющие анализировать ренту не по каждому ее члену в отдельности, а как единую совокупность - рассчитывать ее будущую и приведенную величины, а также определять размеры других важных параметров ренты.

Конверсия финансовых рент - это изменение условий выплат финансовых рент. Примерами конверсии может быть выкуп ренты (замена рентных платежей разовым платежом) или замена разового платежа рентными. Исходя из принципа финансовой эквивалентности, следует, что в первом случае вместо рентных платежей может быть выплачена современная величина ренты, а во втором – вместо единовременного (разового) платежа должны производиться выплаты в рассрочку по схеме рентных платежей.

Именно этими факторами и обусловлена актуальность выбранной темы работы.

Цель работы – рассмотреть конверсию финансовых рент, условия замены ренты с одними условиями на ренту с другими условиями.

Задачи работы обусловлены целью и имеют следующий вид:

- изучить теоретические аспекты конверсии финансовых рент, условия замены ренты с одними условиями на ренту с другими условиями;

- решить практические задачи.

При написании работы использовались учебно-методические пособия отечественных авторов.

1 Конверсия финансовых рент. Замена ренты с одними условиями на ренту с другими условиями

Финансовые операции часто носят продолжительный характер и состоят не из разового платежа, а из их последовательности, т.е. из потока платежей.

Поток платежей, все члены которого положительные величины, а временные интервалы постоянны, называют финансовой рентой или аннуитетом [5, с.46].

Основные правила процентных вычислений, рассмотренные нами ранее, остаются неизменными и для совокупности платежей, однако возникает необходимость ввести несколько дополнительных понятий. В финансовом анализе для обозначения денежных потоков в наиболее общем смысле используется термин рента.

Частным случаем ренты является финансовая рента или аннуитет - такой поток платежей, все члены которого равны друг другу, так же как и интервалы времени между ними.

Часто аннуитетом называют финансовый актив, приносящий фиксированный доход ежегодно в течение ряда лет [7, с.28].

Финансовая рента имеет следующие параметры:

- член ренты - величина каждого отдельного платежа;

- период ренты - временной интервал между двумя соседними платежами, срок ренты - время, измеренное от начала финансовой ренты до конца ее последнего периода;

- процентная ставка - ставка, используемая при наращении или дисконтировании платежей, образующих ренту, число платежей в году, число начислений процентов в году, моменты платежа внутри периода ренты [3, с.62].

Классификация рент может быть произведена по различным признаками.

В зависимости от продолжительности периода, ренты делят на годовые и p-срочные, где p - число выплат в году. По числу начислений процентов различают ренты с начислением один в году, m раз или непрерывно. Моменты начисления процентов могут не совпадать с моментами рентных платежей [5, с.47].

По величине членов различают постоянные (с равными членами) и переменные ренты. Если размеры платежей изменяются по какому - либо математическому закону, то часто появляется возможность вывести стандартные формулы, значительно упрощающие расчеты.

По вероятности выплаты членов различают ренты верные и условные. Верные ренты подлежат безусловной выплате, например, при погашении кредита. Выплата условной ренты ставится в зависимость от наступления некоторого случайного события. Поэтому число ее членов заранее неизвестно. Например, число выплат пенсий зависит от продолжительности жизни пенсионера.

По числу членов различают ренты с конечным числом членов или ограниченные и бесконечные или вечные. В качестве вечной ренты можно рассматривать выплаты по облигационным займам с неограниченными или не фиксированными сроками.

В зависимости от наличия сдвига момента начала ренты по отношению к началу действия контракта или какому-либо другому моменту ренты подразделяются на немедленные и отложенные или отсроченные. Срок немедленных рент начинается сразу, а у отложенных запаздывает.

Анализ потоков платежей в большинстве случаев предполагает расчет наращенной суммы или современной величины ренты.

Рассмотрим расчет современной стоимости и наращенной суммы постоянной обычной (постнумерандо) p - срочной ренты [4, с.84].

Ежегодно сумма R вносится равными долями p раз в году на банковский счет в течение n лет. Тогда имеем поток из np платежей величиной каждый в моменты .

Примем за единицу измерения времени 1 год.

Пусть i - годовая эффективная процентная ставка начисления сложных процентов на поступающие платежи.

Согласно определению современной стоимости потока платежей, получаем:

(1)

Вычисляя сумму np членов геометрической прогрессии, знаменатель которой 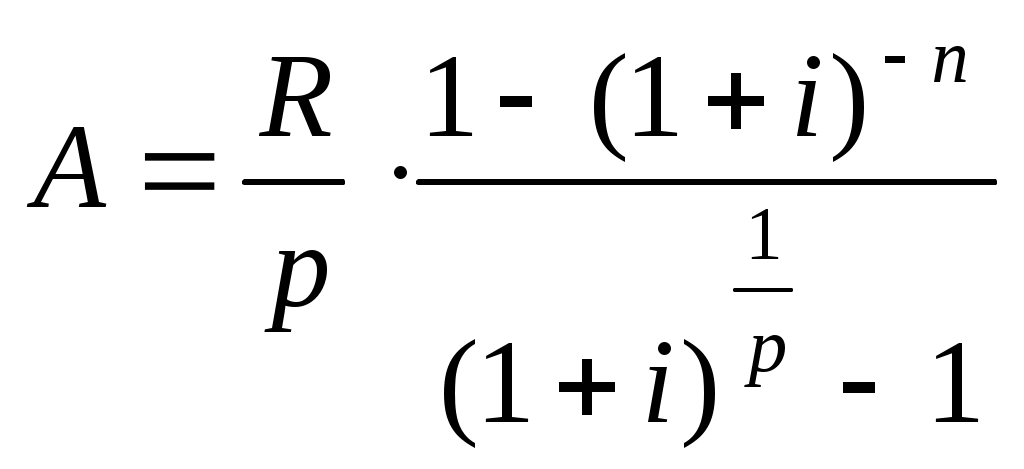, получим:

(2)

Современная стоимость постоянной обычной p - срочной ренты при начислении процентов на члены ренты 1 раз в году в течение n лет.

Отсюда современная стоимость годовой обычной ренты (p = 1) при начислении процентов на члены ренты 1 раз в году:

. (3)

Конверсия финансовых рент - это изменение условий выплат финансовых рент. Примерами конверсии может быть выкуп ренты (замена рентных платежей разовым платежом) или замена разового платежа рентными. Исходя из принципа финансовой эквивалентности, следует, что в первом случае вместо рентных платежей может быть выплачена современная величина ренты, а во втором – вместо единовременного (разового) платежа должны производиться выплаты в рассрочку по схеме рентных платежей.

Если по тем или иным причинам необходимо изменить условия контракта, то речь идет о конвертировании условий ренты. Простейшие случаи конверсии рент следующие:

- замена ренты разовым платежом (выкуп ренты);

- объединение рент в одну (консолидация рент);

- замена ренты с одними условиями на ренту с другими условиями.

При решении этих задач используется принцип финансовой эквивалентности. Поясним его применение в каждом из перечисленных случаев.

Выкуп ренты.

Смысл этой операции состоит в замене ренты (серии платежей) одним единовременным платежом.

Право плательщика на выкуп постоянной ренты регулируется ст. 592 Гражданского Кодекса Российской Федерации [1]. В соответствии с данной статьей, Плательщик постоянной ренты вправе отказаться от дальнейшей выплаты ренты путем ее выкупа.

Такой отказ действителен при условии, что он заявлен плательщиком ренты в письменной форме не позднее чем за три месяца до прекращения выплаты ренты или за более длительный срок, предусмотренный договором постоянной ренты. При этом обязательство по выплате ренты не прекращается до получения всей суммы выкупа получателем ренты, если иной порядок выкупа не предусмотрен договором. Условие договора постоянной ренты об отказе плательщика постоянной ренты от права на ее выкуп ничтожно.

Договором может быть предусмотрено, что право на выкуп постоянной ренты не может быть осуществлено при жизни получателя ренты либо в течение иного срока, не превышающего тридцати лет с момента заключения договора.

Искомый размер выкупа должен быть равен современной стоимости выкупаемой ренты. Для решения задачи в зави­симости от условий погашения задолженности выбирается та или иная формула расчета современной стоимости потока пла­тежей. Естественно, что применяемая при расчете современной стоимости процентная ставка должна удовлетворять обе участ­вующие стороны.

В зависимости от типа ренты (пренумерандо, постнумерандо) и ее параметров используется та или иная формула для расчета  и т.д.

Рассрочка платежей.

Эта задача является обратной к описанной в предыдущем пункте. Если вы должны уплатить некоторую большую сумму денег, и есть договоренность погашать ее частями в рассрочку, то это удобно сделать в виде выплаты постоянной ренты. Для решения задачи необходимо приравнять сумму долга и современную стоимость ренты. Тогда, согласно договоренности о типе ренты, задача заключается в определении одного из параметров ренты, зная все остальные. Например, если известен срок погашения n и ставка i, то определяется величина разовой выплаты Y.

Объединение (консолидация) рент.

Консолидация ренты - объединение нескольких рент в одну. Принцип финансовой эквивалентности в данном случае предусматривает выполнение такого равенства.

(4)

где А - современная величина рент, заменяющиеся; Аq - современная величина q - й ренты (q -1, 2,..., к).

В случае объединения рент могут возникнуть самые разнообразные задачи, в частности:

а) определение размера члена объединенной ренты;

б) определение срока объединенной ренты. В обоих случаях должны быть заданы другие параметры рент.

Переменная ренты - это рента, члены которой изменяются в соответствии с какого-то закона развития.

Нерегулярный поток платежей - поток платежей, члены которого изменяются хаотично. Временные интервалы между двумя соседними платежами могут быть любыми. В таком случае обобщающие характеристики получают только путем прямого расчета.

Наращенная сумма:

(5)

Переменная ренты разовыми изменениями членов ренты:

(6)

Длительность ренты равна n. Этот термин распределен на k периодов, в каждом из них член ренты постоянен и равен Rt.

Ренты с постоянным абсолютным приростом платежей. Если а - абсолютный прирост платежей, т.е. а = Rt - Rt - 1, то современная величина ренты определяется по формуле.

(7)

Наращенная сумма:

(8)

Стоит заметить, что в практической деятельности возникают случаи, когда, например, необходимо определиться, как будет осуществляться погашение кредита, когда известно, что покупателю предоставлена отсрочка на три месяца при условии, что проценты за этот период присоединяются к стоимости товаров.

Замена немедленной ренты на отсроченную. При условии, что имеется немедленная рента постнумерандо с параметрами R1, n1, процентная ставка равна r. Необходимо отсрочить выплаты на t лет. Иначе говоря, немедленная рента заменяется на отсроченную с параметрами R2, n2, t ( не входит в срок ренты). Здесь возможны разные постановки задачи в зависимости от того, что задано для новой ренты. Если задан срок, то определяется R2 ,и наоборот. Рассмотрим первую задачу при условии, что   Тогда справедливо следующее выражение:

(9)

Отсюда:

(10)

Т.е. член новой ренты равен наращенному за время t члену заменяемой ренты.

В общем случае, когда   , из равенства   следует:

(11)

Определим срок новой ренты при условии, что размер члена ренты остается без изменений. Из равенства



находим:

(11)

Замена годовой ренты на р-срочную. В этих условиях годовая немедленная рента постнумерандо с параметрами R1, n1 заменяется на р-срочную с параметрами R2, n2, р. Если заданы срок заменяющей ренты, ее периодичность и ставка, то:

(12)

Причем, если 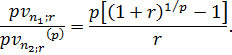  , то:

(13)

Откуда:

(14)

Замена годовой ренты на р-срочную может быть осуществлена и при условии, что заданным является размер члена ренты, тогда определяется ее срок. В общем случае для этого сначала находять:

(15)

Далее по формуле для расчета срока постоянной р-срочной ренты постнумерандо находят   .

Общий случай конверсии.

Выше рассмотрены методы эквивалентной замены некоторых постоянных дискретных рент. Но переход от одного вида к другому возможен для любых потоков платежей. В каждом случае в основу замены должно быть положено равенство соответствующих современных стоимостей потоков платежей. Пусть, например, необходимо заменить нерегулярный поток денег годовой рентой постнумерандо. Пусть поток состоит из платежей Rt, выплачиваемых спустя nt лет после начала действия контракта. Параметрами заменяющей немедленной годовой ренты постнумерандо являются R и n. Исходное уравнение эквивалентности имеет вид: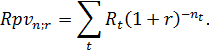

(16)

Данное равенство дает возможность определить один из параметров ренты R или n. Решение обратной задачи – определение членов нерегулярного потока платежей – достигается только подбором величин платежей, удовлетворяющих этому равенству.

Таким образом, рассмотрев теоретические аспекты конверсии финансовых рент, можно сделать вывод, что процесс, связанный с изменением условий ренты, называется конверсией ренты. Иногда конверсия ренты заключается в замене ренты единовременным платежом. Иногда рента с одним набором условий заменяется рентой с другими условиями. При этом предполагается, что конверсия рент не приводит к изменению финансовых последствий для каждого из участвующих в соглашении сторон, то есть она должна основываться на принципе финансовой эквивалентности платежей. При этом находят современную величину данной ренты, а затем подбирают ренту с такой же современной величиной и нужными параметрами.

2 Практические задания

Задача 1

Банк принимает вклады на срочный депозит на следующих условиях: процентная ставка при сроке 35 дней – 3 % годовых; при сроке – 65 дней – 5 % годовых; при сроке 90 дней – 6 % годовых. Определить доход клиента при вкладе 70 000 руб. на указанные сроки.
Решение.

Простые проценты начисляются по формуле:

Б = С*(1 + Т/Тгод*К) - С

Найдем суммы выплат владельцу депозита с разными сроками хранения с использованием простых процентов:

35 дней: Б = 70 000*(1 + 35/365*0,03) – 70 000 = 201,37 руб.

65 дней: Б = 70 000*(1 + 65/365*0,05) – 70 000 = 623,29 руб.

90 дней: Б = 70 000*(1 + 90/365*0,06) – 70 000 = 1035,62 руб.

Задача 2

Определить текущую стоимость денег при простой ставке дисконтирования 3 % годовых, если через 10 лет она обратится в 20 000 долл.
Решение.

К математическому дисконтированию прибегают в тех случаях, когда по известной наращенной сумме (S), процентной ставке (i) и времени обращения (t) необходимо найти первоначальную стоимость (P). При этом предполагается, что проценты начисляются на первоначальную, а не наращенную сумму денег.

Дисконт, как и саму первоначальную сумму, можно находить по схеме простых и сложных процентов.

Первоначальную сумму при простом математическом дисконтировании можно рассчитать по формуле:

P= , (16)

отсюда:

Р = 20 000 / (1+ 0,03 * 10) = 15 384,62 долл.

Задача 3

Инвестор имеет возможность вложить 100 000 руб. на 2 года. Рассчитать минимальную процентную ставку, чтобы окупить затраты инвестора, если известно, что среднегодовой уровень инфляции составит 7,5%.
Решение.

Реальная ставка (r) = номинальная ставка – уровень инфляции.

Реальная процентная ставка – это увеличение реального богатства, выраженное в приросте покупательной способности инвестора, или обменный курс, по которому сегодняшние товары и услуги, реальные блага, обмениваются на будущие товары и услуги. То, что рыночная норма процента испытает непосредственное влияние инфляционных процессов первым предположил И.Фишер, который определял номинальную ставку процента и ожидаемого темпа инфляции.

Взаимосвязь между ставками может быть представлена следующим выражением:

i = r + e, где i – номинальная, или рыночная, ставка процента, r - реальная ставка процента,

е – темп инфляции.

Только в особых случаях, когда на денежном рынке нет повышения цен (е=0), реальная и номинальная процентные ставки совпадают. Уравнение показывает, что номинальная процентная ставка может изменяться вследствие изменений реальной процентной ставки процента или вследствие изменения инфляции. Так как заемщик и кредитор не знают, какие темпы примет инфляция, то они исходят из ожидаемых темпов инфляции. Уравнение обретает вид:

i = r + e^е, где е^е - ожидаемый темп инфляции.

Это уравнение известно, как эффект Фишера. Его суть в том, что номинальная процентная ставка определяется не фактическим темпом инфляции, так как он не известен, а ожидаемым темпом инфляции. Динамика же номинальной процентной ставки повторяет движение ожидаемого темпа инфляции.

Отсюда минимальная ставка процента составит:

i = 0 + 7,5 = 7,5%

Список использованных источников

1. 
   Гражданский Кодекс Российской Федерации, ч. 2.
   
2. 
   Багриновский К. Матюшок В. Экономико-математические метода и модели: Учебник / К. Багриновский, В. Матюшок. - М.: Экономистъ, 2009. - 185с.
   
3. 
   Бочаров П.П., Касимов Ю.Ф. Финансовая математика: Учебник / П.П. Бочаров, Ю.Ф. Касимов. - М.: Гардарики, 2012. - 624с.
   
4. 
   Жуков, Е. Ф. Банки и небанковские кредитные организации и их операции. Учебник / Е.Ф. Жуков. – М.: ЮНИТИ, 2012. – 559 с.
   
5. 
   Ковалев, В. В. Корпоративные финансы и учет: понятия, алгоритмы, показатели [Текст]: учебное пособие / В. В. Ковалев, Вит. В. Ковалев. - 4-е изд., перераб. и доп. - М. : Проспект, 2013 - 873 с.
   
6. 
   Кузнецов Б.Т. Финансовая математика: Учебное пособие / Б.Т. Кузнецов. - М.: Экзамен, 2012. - 128с.
   
7. 
   Кутуков В.Б. Основы финансовой и страховой математики: Методы расчета кредитных, инвестиционных, пенсионных и страховых схем. - М.: Дело, 2008. - 304с.
   
8. 
   Лукашин Ю.П. Финансовая математика: Учебное пособие / Ю.П. Лукашин. - М.: МФПА, 2014. - 81с.
   
9. 
   Львова Н.А. Финансовая диагностика российских предприятий с применением модели Альтмана для развитых и формирующихся рынков // Финансовая аналитика: проблемы и решения. - 2015. - № 7 (241). - С. 37-45.
   
10. 
    Малыхин В.И. Финансовая математика / В.И. Малыхин. - М.: Юнити - Дана, 2013. - 237с.
    
11. 
    Меньшиков С. Рентабельность и рента / С. Меньшиков // Экономическое стратегии. - 2014. - №1. - с.28-31.
    
12. 
    Негашев, Е.В. Аналитическое моделирование финансового состояния компании [Текст]: монография / Е.В. Негашев - М.: НИЦ ИНФРА-М, 2013. - 186 с. - ISBN 978-5-16-009397-0.
    
13. 
    Половинкин, С.А. Управление финансами предприятия [Текст]: учеб. практ. пособие / С.А. Половинкин - М.: ИД ФБК-ПРЕСС, 2014. - 376 с.
    
14. 
    Поляк Г.Б. Финансы и кредит. Учебное пособие / Г.Б. Поляк. – М.: Волтерс Клувер, 2013. – 779 с.
    
15. 
    Пушкарева, В. М. Экономика. Словарь [Текст]: учеб. пособие / В. М. Пушкарева. - М. : Вуз. учебник : ИНФРА-М, 2015. - 229 с.
    
16. 
    Решетникова, О. Е. Финансовое состояние промышленного предприятия как объект финансового анализа / Решетникова О. Е. // Экономический анализ: теория и практика, 2014. - № 39. - С. 94 - 99.
    
17. 
    Чараева, М.В. Финансовый менеджмент: учебное пособие / М.В. Чараева. - 2-е изд. - М.: НИЦ ИНФРА-М, 2014. - 240 с.
    
18. 
    Четыркин Е.М. Финансовая математика / Е.М. Четыркин. - 4-е изд. - М.: Дело, 2014. - 400с.
    
19. 
    Швецова, О. И. Оценка финансовой, инвестиционной деятельности / О. И. Швецова // Экономика - технологии. - 2012. - № 2. - С. 20 - 29.
    
20. 
    Шеремет, А.Д. Финансы предприятий: менеджмент и анализ: учеб­ное пособие - 2-е изд., испр. и доп. / А.Д. Шеремет А.Ф. Ионова. - М.: Инфра - М., 2012. - с. 326.