Задачи по эконометрике. Задача 1 2 Задача 2 23 Список литературы 40
 Скачать 0.82 Mb. Скачать 0.82 Mb.
|
1 2 ОглавлениеЗадача 1 2 Задача 2 23 Список литературы 40 Задача 1Построить эконометрическую модель социально-экономического показателя по Российской Федерации. Требуется исследовать зависимость результирующего признака Y, соответствующего варианту задания, от факторных переменных Х1, Х2и Х3: Исходными данными для моделирования являются
Источник: данные Федеральной службы государственной статистики. – Регионы России. Социально-экономические показатели. https://gks.ru/bgd/regl/b18_14p/Main.htm Исходные данные
Порядок выполнения работы Провести корреляционный анализ: рассчитать матрицу парных коэффициентов корреляции; проанализировать тесноту и направление связи результирующего признака Y с каждым из факторов Х; оценить статистическую значимость коэффициентов корреляции r(Y,Xi); выбрать наиболее информативный фактор; проанализировать связи между факторами на наличие мультиколлинеарности. Построить модель парной регрессии с наиболее информативным фактором. Оценить влияние факторной переменной на Y по коэффициенту регрессии Исследовать качество модели, используя среднюю относительную погрешность аппроксимации, критерий Фишера, коэффициент детерминации и t-статистики коэффициентов регрессии (принять уровень значимости α=5%); сделать выводы о качестве модели: С доверительной вероятностью γ=80% осуществить прогнозирование среднего значения показателя Y. Представить графически фактические и модельные значения Y, результаты прогнозирования. Оценить параметры линейной модели с полным перечнем факторов. Оценить влияние факторных переменных на Y по коэффициентам регрессии. Оценить качество трехфакторной модели с помощью средней относительной ошибки аппроксимации, коэффициента детерминации, F – критерия Фишера и t-статистики коэффициентов регрессии. Построить двухфакторную модель, включив в нее наиболее подходящие факторы на основе корреляционного анализа (объяснить выбор переменных). Дать экономическую интерпретацию ее коэффициентов. Оценить качество построенной модели, аналогично предыдущим моделям. Провести сравнительный анализ для выявления лучшей модели среди трех построенных. Улучшилось ли качество множественной модели по сравнению с парной? Для лучшей многофакторной модели вычислить коэффициенты эластичности, бета- и дельта- коэффициенты, сделать выводы. Для лучшей многофакторной модели выполнить точечный прогноз Y для заданных прогнозных значений Х*. Решение 1.Провести корреляционный анализ: а) рассчитать матрицу парных коэффициентов корреляции Используем Excel (Данные / Анализ данных / КОРРЕЛЯЦИЯ): 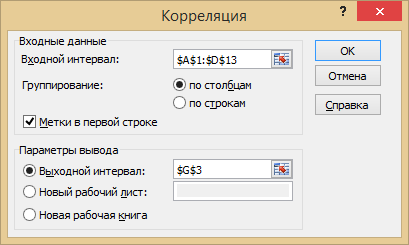 Получим матрицу коэффициентов парной корреляции между всеми имеющимися переменными: 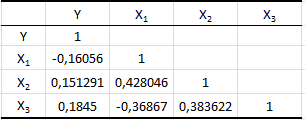 б) проанализировать тесноту и направление связи результирующего признака Y с каждым из факторов Х 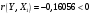 , следовательно, между переменными Y и Х1 наблюдается обратная корреляционная зависимость: доля потребительских расходов на предметы домашнего обихода, бытовую техника и уход за домом на душу населения (в год), ниже для среднедушевых денежных доходов (в месяц). , следовательно, между переменными Y и Х1 наблюдается обратная корреляционная зависимость: доля потребительских расходов на предметы домашнего обихода, бытовую техника и уход за домом на душу населения (в год), ниже для среднедушевых денежных доходов (в месяц).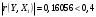 – зависимость слабая – зависимость слабая 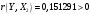 , значит, между переменными Y и Х2 наблюдается прямая корреляционная зависимость: доля потребительских расходов на предметы домашнего обихода, бытовую техника и уход за домом на душу населения (в год), выше чем среднемесячная номинальная начисленная заработная плата работников организаций. , значит, между переменными Y и Х2 наблюдается прямая корреляционная зависимость: доля потребительских расходов на предметы домашнего обихода, бытовую техника и уход за домом на душу населения (в год), выше чем среднемесячная номинальная начисленная заработная плата работников организаций.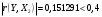 – зависимость слабая – зависимость слабая 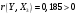 , значит, между переменными Y и Х3 наблюдается прямая корреляционная зависимость: доля потребительских расходов на предметы домашнего обихода, бытовую техника и уход за домом на душу населения (в год), выше чем индекс потребительских цен (декабрь к декабрю предыдущего года). , значит, между переменными Y и Х3 наблюдается прямая корреляционная зависимость: доля потребительских расходов на предметы домашнего обихода, бытовую техника и уход за домом на душу населения (в год), выше чем индекс потребительских цен (декабрь к декабрю предыдущего года).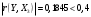 – зависимость слабая – зависимость слабая в) оценить статистическую значимость коэффициентов корреляции 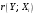 ; выбрать наиболее информативный фактор ; выбрать наиболее информативный факторДля проверки значимости найденных коэффициентов корреляции используем критерий Стьюдента. Для каждого коэффициента корреляции 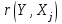 вычислим t-статистику по формуле: вычислим t-статистику по формуле: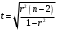 и занесем результаты расчетов в дополнительный столбец корреляционной таблицы: 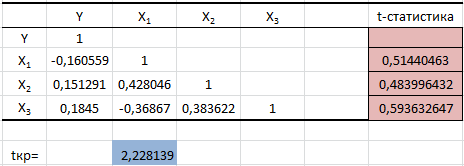 По таблице критических точек распределения Стъюдента при уровне значимости 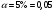 и числе степеней свободы и числе степеней свободы 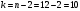 , определим критическое значение , определим критическое значение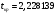 (функция СТЬЮДРАСПОБР). (функция СТЬЮДРАСПОБР).Сопоставим фактические значения t с критическим tкp, и сделаем выводы в соответствии со схемой: 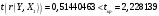 , следовательно, коэффициент , следовательно, коэффициент 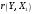 не является значимым. не является значимым. 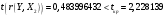 , следовательно, коэффициент , следовательно, коэффициент 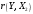 не является значимым. не является значимым.  , следовательно, коэффициент , следовательно, коэффициент 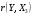 не является значимым. не является значимым. г) проанализировать связи между факторами на наличие мультиколлинеарности. Если в матрице есть межфакторный коэффициент корреляции 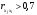 , то в данной модели множественной регрессии существует мультиколлинеарность. , то в данной модели множественной регрессии существует мультиколлинеарность.В нашем случае все парные коэффициенты корреляции 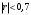 , что говорит об отсутствии сильной мультиколлинеарности факторов. Целесообразно оставить все факторы. , что говорит об отсутствии сильной мультиколлинеарности факторов. Целесообразно оставить все факторы.2.Построить модель парной регрессии с наиболее информативным фактором. Оценить влияние факторной переменной на Y по коэффициенту регрессии Наиболее информативным фактором является тот, для которого связь между ним и Y наиболее тесная, т.е. коэффициент корреляции наибольший по абсолютной величине (по модулю) Наибольшее влияние на результативный признак оказывает фактор Х3 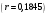 , значит, при построении модели он войдет в регрессионное уравнение первым. , значит, при построении модели он войдет в регрессионное уравнение первым. Для построения парной линейной модели 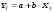 используем программу РЕГРЕССИЯ (Данные / Анализ данных). В качестве «входного интервала Х» покажем значения фактора Х3. используем программу РЕГРЕССИЯ (Данные / Анализ данных). В качестве «входного интервала Х» покажем значения фактора Х3.Результаты вычислений представлены в таблицах: 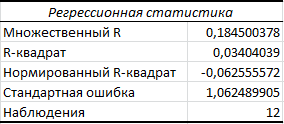   Коэффициенты модели содержатся в третьей таблице итогов РЕГРЕССИИ (столбец Коэффициенты). Таким образом, модель парной регрессии построена, ее уравнение имеет вид 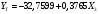 С увеличением индекса потребительских цен (декабрь к декабрю предыдущего года) на 1 % доля потребительских расходов на предметы домашнего обихода, бытовую техника и уход за домом увеличится на 0,3765 % 3.Исследовать качество модели, используя среднюю относительную погрешность аппроксимации, критерий Фишера, коэффициент детерминации и t-статистики коэффициентов регрессии (принять уровень значимости α=5%); сделать выводы о качестве модели: Коэффициент детерминации R-квадрат определен программой РЕГРЕССИЯ (таблица «Регрессионная статистика») и составляет R2=0,034. Таким образом, вариация (изменение) доли потребительских расходов на предметы домашнего обихода, бытовую технику и уход за домом на 3,4% объясняется по уравнению модели вариацией среднедушевых доходов. Проверим значимость полученного уравнения с помощью F – критерия Фишера. F – статистика определена программой РЕГРЕССИЯ (таблица «Дисперсионный анализ») и составляет 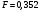 . .Критическое значение 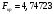 найдено для уровня значимости =5% и чисел степеней свободы найдено для уровня значимости =5% и чисел степеней свободы 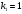 , , 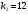 (функция FРАСПОБР). (функция FРАСПОБР).Схема проверки: Сравнение показывает: 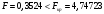 , следовательно, уравнение модели является не значимым, его использование не целесообразно, зависимая переменная Y(доля потребительских расходов на предметы домашнего обихода, бытовую технику и уход за домом, %) не достаточно хорошо описывается включенной в модель факторной переменной Х3 (индекс потребительских цен (декабрь к декабрю предыдущего года)). , следовательно, уравнение модели является не значимым, его использование не целесообразно, зависимая переменная Y(доля потребительских расходов на предметы домашнего обихода, бытовую технику и уход за домом, %) не достаточно хорошо описывается включенной в модель факторной переменной Х3 (индекс потребительских цен (декабрь к декабрю предыдущего года)).Значимость коэффициентов модели проверим с помощью t – критерия Стьюдента. t – статистики для коэффициентов уравнения регрессии приведены в столбце «t–статистика» третьей таблицы итогов РЕГРЕССИИ: для свободного коэффициента 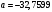 определена статистика определена статистика 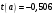 . .для коэффициента регрессии 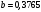 определена статистика определена статистика 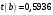 . .Критическое значение 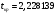 найдено для уровня значимости =5% и числа степеней свободы 10 (функция СТЬЮДРАСПОБР). найдено для уровня значимости =5% и числа степеней свободы 10 (функция СТЬЮДРАСПОБР).Схема проверки: 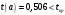 свободный коэффициент а является не значимым. свободный коэффициент а является не значимым.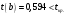 коэффициент регрессии b является не значимым. коэффициент регрессии b является не значимым.Выводы о значимости коэффициентов модели сделаны на уровне значимости =5%. Рассматривая столбец «Р-значение», отметим, что свободный коэффициент а можно считать незначимым на уровне 0,6238; коэффициент регрессии b – на уровне 0,566. Для вычисления средней относительной ошибки аппроксимации дополним таблицу относительных погрешностей, которые вычислим по формуле 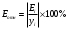 с помощью функции ABS с помощью функции ABS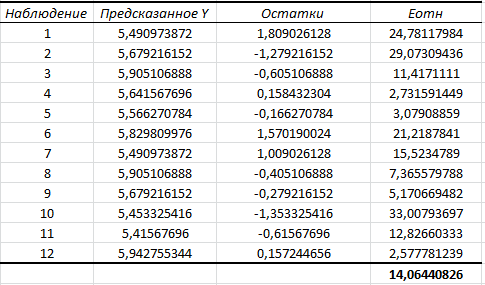 По столбцу относительных погрешностей найдем среднее значение 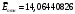 (функция СРЗНАЧ). (функция СРЗНАЧ).Сравним:  , следовательно, точность модели удовлетворительная. , следовательно, точность модели удовлетворительная. 4.С доверительной вероятностью γ=80% осуществить прогнозирование среднего значения показателя Y. Представить графически фактические и модельные значения Y, результаты прогнозирования. Построим уравнение тренда 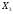 при при 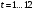  По полученному уравнению тренда найдем прогнозное значение X3 для 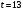 . .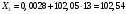 Примем прогнозное значение факторной переменной Х3 составляет 102,54%. Рассчитаем по уравнению модели прогнозное значение показателя Y: 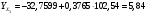 Таким образом, если индекс потребительских цен составит 102,54%, то доля потребительских расходов на предметы домашнего обихода, бытовую технику и уход за домом будет около 5,84%. Зададим доверительную вероятность 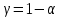 и построим доверительный прогнозный интервал для среднего значения Y. и построим доверительный прогнозный интервал для среднего значения Y.Для этого нужно рассчитать стандартную ошибку прогнозирования для среднего значения результирующего признака 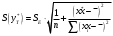 . .Предварительно подготовим: стандартную ошибку модели SE=1,0625 (таблица «Регрессионная статистика» итогов РЕГРЕССИИ); по столбцу исходных данных Х3 найдем среднее значение равное 102,7 (функция СРЗНАЧ) и определим 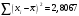 (функция КВАДРОТКЛ); (функция КВАДРОТКЛ);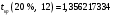 (функция СТЬЮДРАСПОБР). (функция СТЬЮДРАСПОБР).Получаем: 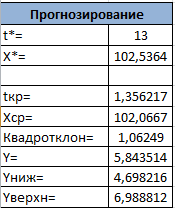 Для построения чертежа используем Мастер диаграмм (точечная) – покажем исходные данные (поле корреляции). 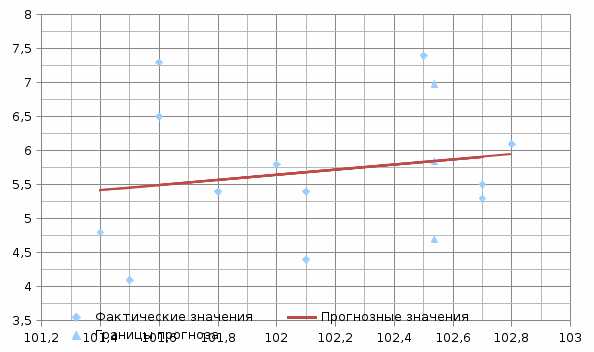 5.Оценить параметры линейной модели с полным перечнем факторов. Оценить влияние факторных переменных на Y по коэффициентам регрессии. Строим при помощи РЕГРЕССИИ линейную модель с полным перечнем факторов: 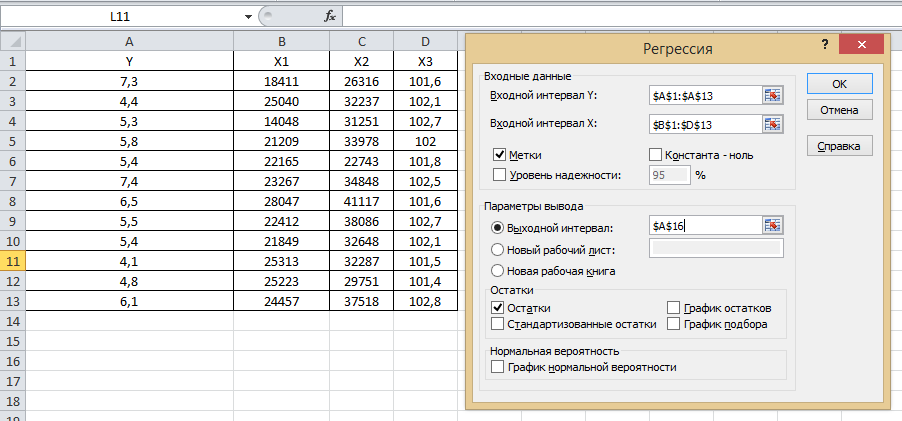 Получаем: 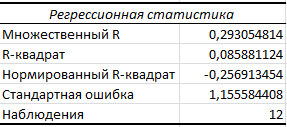   Уравнение регрессии имеет вид: 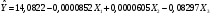 Коэффициент регрессии  , следовательно, при увеличении среднедушевых денежных доходов (Х1) на 1 руб. и неизменных остальных факторах доля потребительских расходов на предметы домашнего обихода, бытовую технику и уход за домом (Y) уменьшается в среднем на 0,00008522%. , следовательно, при увеличении среднедушевых денежных доходов (Х1) на 1 руб. и неизменных остальных факторах доля потребительских расходов на предметы домашнего обихода, бытовую технику и уход за домом (Y) уменьшается в среднем на 0,00008522%.Коэффициент регрессии 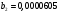 , следовательно, при увеличении среднемесячной номинальной начисленной заработной платы работников организаций (Х2) на 1 руб. и неизменных остальных факторах доля потребительских расходов на предметы домашнего обихода, бытовую технику и уход за домом (Y) увеличится в среднем на 0,0000605%. , следовательно, при увеличении среднемесячной номинальной начисленной заработной платы работников организаций (Х2) на 1 руб. и неизменных остальных факторах доля потребительских расходов на предметы домашнего обихода, бытовую технику и уход за домом (Y) увеличится в среднем на 0,0000605%.Коэффициент регрессии 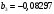 , следовательно, доля потребительских расходов на предметы домашнего обихода, бытовую технику и уход за домом (Y) в среднем на 0,08297% ниже, чем в предыдущем году при неизменных остальных факторах. , следовательно, доля потребительских расходов на предметы домашнего обихода, бытовую технику и уход за домом (Y) в среднем на 0,08297% ниже, чем в предыдущем году при неизменных остальных факторах.Свободный коэффициент не имеет экономического смысла. 6.Оценить качество трехфакторной модели с помощью средней относительной ошибки аппроксимации, коэффициента детерминации, F – критерия Фишера и t-статистики коэффициентов регрессии. Коэффициент детерминации R-квадрат определен программой РЕГРЕССИЯ (таблица «Регрессионная статистика») и составляет R2=0,0859. Таким образом, вариация (изменение) доли потребительских расходов на предметы домашнего обихода, бытовую технику и уход за домом на 8,59% объясняется по уравнению модели вариацией среднедушевых доходов и номинальной начисленной заработной платой. Проверим значимость полученного уравнения с помощью F – критерия Фишера. F – статистика определена программой РЕГРЕССИЯ (таблица «Дисперсионный анализ») и составляет 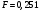 . .Критическое значение 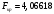 найдено для уровня значимости =5% и чисел степеней свободы найдено для уровня значимости =5% и чисел степеней свободы  , ,  (функция FРАСПОБР). (функция FРАСПОБР).Схема проверки: Сравнение показывает:  , следовательно, уравнение модели является не значимым, его использование не целесообразно, зависимая переменная Y(доля потребительских расходов на предметы домашнего обихода, бытовую технику и уход за домом, %) не достаточно хорошо описывается включенной в модель факторной переменной Х3 (индекс потребительских цен (декабрь к декабрю предыдущего года)). , следовательно, уравнение модели является не значимым, его использование не целесообразно, зависимая переменная Y(доля потребительских расходов на предметы домашнего обихода, бытовую технику и уход за домом, %) не достаточно хорошо описывается включенной в модель факторной переменной Х3 (индекс потребительских цен (декабрь к декабрю предыдущего года)).Значимость коэффициентов модели проверим с помощью t – критерия Стьюдента. t – статистики для коэффициентов уравнения регрессии приведены в столбце «t–статистика» третьей таблицы итогов РЕГРЕССИИ: для свободного коэффициента  определена статистика определена статистика 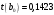 . .для коэффициента регрессии 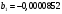 определена статистика определена статистика 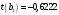 . .для коэффициента регрессии 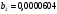 определена статистика определена статистика  . .для коэффициента регрессии  определена статистика определена статистика  . .Критическое значение  найдено для уровня значимости =5% и числа степеней свободы 8 (функция СТЬЮДРАСПОБР). найдено для уровня значимости =5% и числа степеней свободы 8 (функция СТЬЮДРАСПОБР).Схема проверки:  свободный коэффициент b0 является не значимым. свободный коэффициент b0 является не значимым. коэффициент регрессии b1 является не значимым. коэффициент регрессии b1 является не значимым. коэффициент регрессии b2 является не значимым. коэффициент регрессии b2 является не значимым. коэффициент регрессии b3 является не значимым. коэффициент регрессии b3 является не значимым.Выводы о значимости коэффициентов модели сделаны на уровне значимости =5%. Рассматривая столбец «Р-значение», отметим, что свободный коэффициент b0 можно считать незначимым на уровне 0,89; коэффициент регрессии b1 – на уровне 0,551; коэффициент регрессии b2 – на уровне 0,561; коэффициент регрессии b3 – на уровне 0,934. Для вычисления средней относительной ошибки аппроксимации дополним таблицу относительных погрешностей, которые вычислим по формуле  с помощью функции ABS с помощью функции ABS По столбцу относительных погрешностей найдем среднее значение  (функция СРЗНАЧ). (функция СРЗНАЧ).Сравним:  , следовательно, точность модели удовлетворительная. , следовательно, точность модели удовлетворительная. 7.Построить двухфакторную модель, включив в нее наиболее подходящие факторы на основе корреляционного анализа (объяснить выбор переменных). Дать экономическую интерпретацию ее коэффициентов.  Из корреляционной матрицы видно, что коэффициенты корреляции  и и  по модулю больше коэффициента корреляции по модулю больше коэффициента корреляции  . Следовательно факторы, которые войдут в модель – Х1 и Х3. . Следовательно факторы, которые войдут в модель – Х1 и Х3.Строим при помощи РЕГРЕССИИ линейную модель с полным перечнем факторов:  Получаем:    Уравнение регрессии имеет вид:  Коэффициент регрессии  , следовательно, при увеличении среднедушевых денежных доходов (Х1) на 1 руб. и неизменных остальных факторах доля потребительских расходов на предметы домашнего обихода, бытовую технику и уход за домом (Y) уменьшается в среднем на 0,00003018%. , следовательно, при увеличении среднедушевых денежных доходов (Х1) на 1 руб. и неизменных остальных факторах доля потребительских расходов на предметы домашнего обихода, бытовую технику и уход за домом (Y) уменьшается в среднем на 0,00003018%.Коэффициент регрессии  , следовательно, доля потребительских расходов на предметы домашнего обихода, бытовую технику и уход за домом (Y) в среднем на 0,08297% ниже, чем в предыдущем году при неизменных остальных факторах. , следовательно, доля потребительских расходов на предметы домашнего обихода, бытовую технику и уход за домом (Y) в среднем на 0,08297% ниже, чем в предыдущем году при неизменных остальных факторах.Свободный коэффициент не имеет экономического смысла. 8.Оценить качество построенной модели, аналогично предыдущим моделям. Коэффициент детерминации R-квадрат определен программой РЕГРЕССИЯ (таблица «Регрессионная статистика») и составляет R2=0,044. Таким образом, вариация (изменение) доли потребительских расходов на предметы домашнего обихода, бытовую технику и уход за домом на 4,4% объясняется по уравнению модели вариацией среднедушевых доходов и номинальной начисленной заработной платой. Проверим значимость полученного уравнения с помощью F – критерия Фишера. F – статистика определена программой РЕГРЕССИЯ (таблица «Дисперсионный анализ») и составляет  . .Критическое значение  найдено для уровня значимости =5% и чисел степеней свободы найдено для уровня значимости =5% и чисел степеней свободы  , ,  (функция FРАСПОБР). (функция FРАСПОБР).Схема проверки: Сравнение показывает:  , следовательно, уравнение модели является не значимым, его использование не целесообразно, зависимая переменная Y(доля потребительских расходов на предметы домашнего обихода, бытовую технику и уход за домом, %) не достаточно хорошо описывается включенной в модель факторной переменной Х3 (индекс потребительских цен (декабрь к декабрю предыдущего года)). , следовательно, уравнение модели является не значимым, его использование не целесообразно, зависимая переменная Y(доля потребительских расходов на предметы домашнего обихода, бытовую технику и уход за домом, %) не достаточно хорошо описывается включенной в модель факторной переменной Х3 (индекс потребительских цен (декабрь к декабрю предыдущего года)).Значимость коэффициентов модели проверим с помощью t – критерия Стьюдента. t – статистики для коэффициентов уравнения регрессии приведены в столбце «t–статистика» третьей таблицы итогов РЕГРЕССИИ: для свободного коэффициента  определена статистика определена статистика 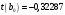 . .для коэффициента регрессии 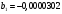 определена статистика определена статистика 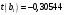 . .для коэффициента регрессии 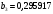 определена статистика определена статистика  . .Критическое значение  найдено для уровня значимости =5% и числа степеней свободы 9 (функция СТЬЮДРАСПОБР). найдено для уровня значимости =5% и числа степеней свободы 9 (функция СТЬЮДРАСПОБР).Схема проверки:  свободный коэффициент b0 является не значимым. свободный коэффициент b0 является не значимым. коэффициент регрессии b1 является не значимым. коэффициент регрессии b1 является не значимым.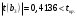 коэффициент регрессии b3 является не значимым. коэффициент регрессии b3 является не значимым.Выводы о значимости коэффициентов модели сделаны на уровне значимости =5%. Рассматривая столбец «Р-значение», отметим, что свободный коэффициент b0 можно считать незначимым на уровне 0,7542; коэффициент регрессии b1 – на уровне 0,767; коэффициент регрессии b3 – на уровне 0,6888. Для вычисления средней относительной ошибки аппроксимации дополним таблицу относительных погрешностей, которые вычислим по формуле 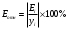 с помощью функции ABS с помощью функции ABS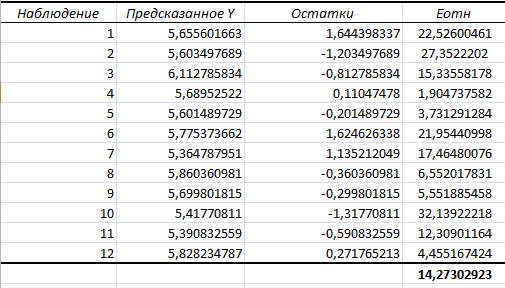 По столбцу относительных погрешностей найдем среднее значение 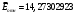 (функция СРЗНАЧ). (функция СРЗНАЧ).Сравним:  , следовательно, точность модели удовлетворительная. , следовательно, точность модели удовлетворительная. 9.Провести сравнительный анализ для выявления лучшей модели среди трех построенных. Улучшилось ли качество множественной модели по сравнению с парной? Для сравнения моделей с различным количеством учтенных в них факторов используем нормированные коэффициенты детерминации, которые содержаться в строке «нормированный R-квадрат» итогов программы РЕГРЕССИЯ. Чем больше величина нормированного коэффициента детерминации, тем лучше модель. Для первой модели:  Для второй модели:  Для третьей модели  Таким образом, лучшей является вторая модель:  10.Для лучшей многофакторной модели вычислить коэффициенты эластичности, бета- и дельта- коэффициенты, сделать выводы. Коэффициент эластичности  показывает, на сколько процентов изменится в среднем переменная Y при увеличении фактора показывает, на сколько процентов изменится в среднем переменная Y при увеличении фактора 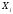 на 1% и неизменных значениях остальных факторов, закрепленных на их средних уровнях. на 1% и неизменных значениях остальных факторов, закрепленных на их средних уровнях.Средние коэффициенты эластичности в случае линейной модели определяются формулами 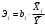 где – где – 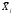 ; ; 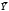 выборочные средние признаков выборочные средние признаков  и и  ; ;  – коэффициенты регрессии. – коэффициенты регрессии. Подготовим  ; ; 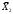 ; ; ; ;  . . Получим 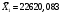 ; ; 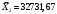 ; ;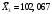 ; ; 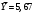 Вычислим: 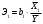 ; ; 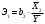 ; ; 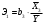 Получим: 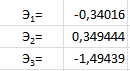 Следовательно: увеличение Х1 на 1% приводит к уменьшению Y в среднем на 0,3401% (при неизменных остальных факторах). увеличение Х2 на 1% приводит к увеличению Y в среднем на 0,3494% (при неизменных остальных факторах). Увеличение Х3 на 1% приводит к уменьшению Y в среднем на 1,4944% (при неизменных остальных факторах). Коэффициент Бета-коэффициенты определяются формулами 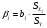 , где , где 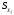 ; ;  – выборочные средние квадратичные (стандартные) отклонения признаков – выборочные средние квадратичные (стандартные) отклонения признаков 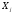 и и 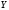 ; ;  – коэффициенты регрессии. – коэффициенты регрессии.Величины   ; подготовим с помощью функции СТАНДОТКЛОН: ; подготовим с помощью функции СТАНДОТКЛОН: Рассчитаем: Вычислим:  ; ; ; ;  . .Таким образом:  при увеличении только фактора Х1 на одно его стандартное отклонение – уменьшается в среднем на 0,3024  , , при увеличении только фактора Х2 на одно его стандартное отклонение – увеличивается в среднем на 0,2963  , , при увеличении только фактора Х3 на одно его стандартное отклонение – уменьшается в среднем на 0,0407  . .С помощью дельта–коэффициентов оценивается доля влияния каждого фактора в суммарном воздействии на результат всех факторов, учтенных в модели. Дельта-коэффициенты определяются формулами:  где 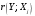 – соответствующие выборочные коэффициенты парной корреляции. – соответствующие выборочные коэффициенты парной корреляции.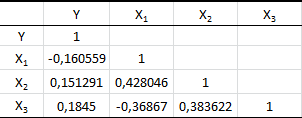 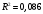 определен для рассматриваемой множественной модели программой РЕГРЕССИЯ определен для рассматриваемой множественной модели программой РЕГРЕССИЯ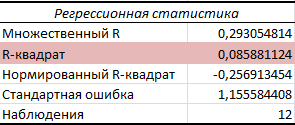 Вычислим дельта-коэффициенты  Значит, по уравнению полученной линейной трехфакторной модели изменение результирующего фактора Y на 0,565% объясняется воздействием фактора Х1; на 0,522% фактора 0,522% и на -0,5087% влиянием фактора Х3. 11.Для лучшей многофакторной модели выполнить точечный прогноз Y для заданных прогнозных значений Х*. Прогнозирование – это оценка значений результирующего показателя Y в некоторой, представляющей практический интерес прогнозной ситуации, которая описывается факторными переменными Х*. Прогнозные значения Х* факторных переменных либо задаются, либо рассчитываются отдельно. Предполагают, что в период прогнозирования сохраняются существующие взаимосвязи между переменными. По уравнениям трендов находим прогнозные значения факторных переменных:  , ,  ; ;  Тогда  Таким образом, если среднедушевые денежные доходы (в месяц), 26159,63 руб., номинальная заработная плата 3622,54 руб., а индекс потребительских цен 102,54%, то ожидаемое значение доли потребительских расходов на предметы домашнего обихода, бытовую технику и уход за домом будет равно 7,67%. 1 2 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
