Задачи по эконометрике. Задача 1 2 Задача 2 23 Список литературы 40
 Скачать 0.82 Mb. Скачать 0.82 Mb.
|
1 2 Задача 2Исследование динамики экономического показателя на основе анализа одномерного временного ряда На основе временного рядаY(t) требуется исследовать динамику социально-экономического показателя по Алтайскому краю за период с 2010 г. по 2018 г. (показатель выбирается в соответствии с вариантом работы).
Порядок выполнения работы Проверить наличие аномальных наблюдений, используя метод Ирвина (α=5%). Построить линейную модель временного ряда yt=a+b∙t, параметры которой оценить МНК. Пояснить смысл коэффициента регрессии. Оценить адекватность посторенной модели, используя свойства независимости остаточной компоненты, случайности и соответствия нормальному закону распределения. Оценить качество модели, используя среднюю относительную погрешность аппроксимации, критерий Фишер и коэффициент детерминации. Осуществить прогнозирование рассматриваемого показателя на год вперед (прогнозный интервал рассчитать при доверительной вероятности 70%). Представить графически фактические значения показателя, результаты моделирования и прогнозирования. Провести расчет параметров логарифмического, полиномиального (полином 2-й степени), степенного, экспоненциального и гиперболического трендов. На основании графического изображения и значения индекса детерминации выбрать наиболее подходящий вид тренда. Составить уравнения нелинейной регрессии (гиперболической; степенной; показательной, полиномиальной) По каждой модели: привести графики построенных уравнений регрессии; найти средние относительные ошибки аппроксимации, коэффициенты детерминации и коэффициенты эластичности. По этим характеристикам сравнить нелинейные модели между собой и сделать вывод. Лучшую нелинейную модель сравнить с лучшей линейной моделью. С помощью лучшей нелинейной модели осуществить точечное прогнозирование рассматриваемого показателя на год вперед. Сопоставить полученный результат с доверительным прогнозным интервалом, построенным при использовании линейной модели. Источник: данные Федеральной службы государственной статистики. – Регионы России. Социально-экономические показатели. Исходные данные
Решение 1.Проверим наличие аномальных наблюдений, используя метод Ирвина (α=5%). Подготовим 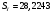 (СТАНДОТКЛОН) и рассчитаем статистики (СТАНДОТКЛОН) и рассчитаем статистики 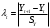 (ABS) (ABS)Результаты расчетов приведем в таблице:
Критическое значение при n = 8 и уровне значимости α = 1% составляет 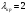 . Аномальных наблюдений нет. . Аномальных наблюдений нет.2.Построить линейную модель временного ряда 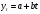 , параметры которой оценить МНК. Пояснить смысл коэффициента регрессии. , параметры которой оценить МНК. Пояснить смысл коэффициента регрессии.С помощью программы «РЕГРЕССИЯ» найдем  Таким образом, 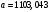 ; ;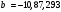 . .Модель построена, ее уравнение имеет вид 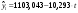 . .Коэффициент регрессии 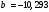 показывает, что с каждым годом социально-экономический показатель Y5 уменьшается в среднем на 10,293 тыс. чел. показывает, что с каждым годом социально-экономический показатель Y5 уменьшается в среднем на 10,293 тыс. чел.3.Оценить адекватность построенной модели, используя свойства независимости остаточной компоненты, случайности и соответствия нормальному закону распределения. Проверка перечисленных свойств состоит в исследовании Ряда остатков et, который содержится в таблице «Вывод остатка» итогов РЕГРЕССИИ. 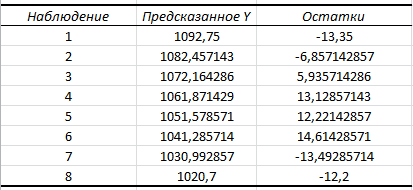 Для проверки свойства случайности остаточной компоненты используем критерий поворотных точек (пиков), основой которого является определение количества поворотных точек для ряда остатков. Программа РЕГРЕССИЯ построила график остатков et.  Поворотными считаются точки максимумов и минимумов на этом графике (в данном случае – четвертая, пятая, шестая и седьмая). Их количество  . .По формуле 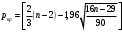 при при 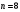 вычислим критическое значение вычислим критическое значение 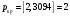 . .Сравним значения pи pкр и сделаем вывод согласно схеме: 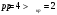 < < 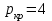 , следовательно, свойство случайности для ряда остатков выполняется. , следовательно, свойство случайности для ряда остатков выполняется.Для проверки свойства независимости остаточной компоненты используем критерий Дарбина-Уотсона. Согласно этому критерию вычислим по формуле статистику 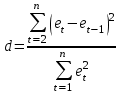 . .Подготовим для вычислений: 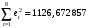 (функция СУММКВ), (функция СУММКВ), 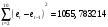 (функция СУММКВРАЗН). (функция СУММКВРАЗН).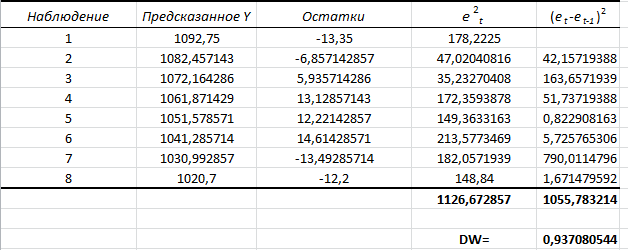 Таким образом, 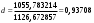 . . По таблице d – статистик Дарбина – Уотсона определим критические уровни: нижний d1 = 0,97 и верхний d2 = 1,33. Сравним полученную фактическую величину d с критическими уровнями d1 и d2 и сделаем вывод согласно схеме:  d = 0,93708 ϵ (0; d1 = 0,97), следовательно, свойство независимости остатков для построенной модели не выполняется. Для проверки соответствия ряда остатков нормальному закону распределения используется R/S критерий. В соответствии с этим критерием вычислим по формуле статистику 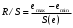 . .Подготовим для вычислений:  – максимальный уровень ряда остатков (функция МАКС); – максимальный уровень ряда остатков (функция МАКС); 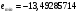 – минимальный уровень ряда остатков (функция МИН); – минимальный уровень ряда остатков (функция МИН);  – стандартная ошибка модели (таблица «Регрессионная статистика» вывода итогов РЕГРЕССИИ). – стандартная ошибка модели (таблица «Регрессионная статистика» вывода итогов РЕГРЕССИИ).Получим 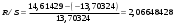 . .По таблице критических границ отношения R/S определим критический интервал. При n = 8 можно использовать (2,70; 3,70). Сопоставим фактическую величину R/S с критическим интервалом и сделаем вывод согласно схеме: 2,06648428 (2,90; 3,70), значит, для построенной модели свойство нормального распределения остаточной компоненты не выполняется. Таким образом, данная трендовая модель не является адекватной реальному ряду наблюдений, для построения прогнозных оценок лучше использовать нелинейные модели или модели авторегрессии. 4.Оценить качество модели, используя среднюю относительную погрешность аппроксимации, критерий Фишер и коэффициент детерминации. Коэффициент детерминации R-квадрат определен программой РЕГРЕССИЯ (таблица «Регрессионная статистика») и составляет R2=0,79795. Таким образом, вариация (изменение) числа людей, занятых в экономике на 79,8% объясняется по уравнению модели вариацией t. Проверим значимость полученного уравнения с помощью F – критерия Фишера. F – статистика определена программой РЕГРЕССИЯ (таблица «Дисперсионный анализ») и составляет 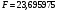 . .Критическое значение  найдено для уровня значимости =5% и чисел степеней свободы найдено для уровня значимости =5% и чисел степеней свободы 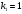 , , 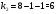 (функция FРАСПОБР). (функция FРАСПОБР).Схема проверки: Сравнение показывает: 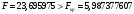 , следовательно, уравнение модели является значимым, его использование целесообразно. , следовательно, уравнение модели является значимым, его использование целесообразно.Для вычисления средней относительной ошибки аппроксимации дополним таблицу относительных погрешностей, которые вычислим по формуле 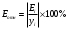 с помощью функции ABS с помощью функции ABS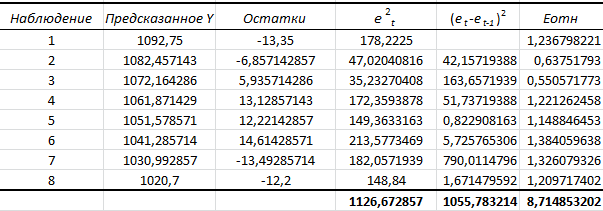 По столбцу относительных погрешностей найдем среднее значение 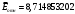 (функция СРЗНАЧ). (функция СРЗНАЧ).Сравним: 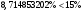 , следовательно, точность модели удовлетворительная. , следовательно, точность модели удовлетворительная. 5.Осуществить прогнозирование рассматриваемого показателя на год вперед (прогнозный интервал рассчитать при доверительной вероятности 70%). «Следующий год» соответствует периоду упреждения k = 1, при этом t* = n+k = 9. Согласно уравнению модели получим точечную прогнозную оценку: 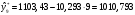 Таким образом, ожидаемый социально-экономический показатель по Алтайскому краю Y5 на следующий год будет составлять около 1010,793. Для оценки точности прогнозирования рассчитаем границы прогнозных интервалов для индивидуальных значений результирующего признака (доверительная вероятность p = 70%). Подготовим: tкр = 1,1342 (функция СТЬЮДРАСПОБР при α = 30%, k = 8 – 2 = 6); S(e) = 13,70324 (строка «стандартная ошибка» итогов РЕГРЕССИИ); 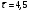 (функция СРЗНАЧ); (функция СРЗНАЧ);  (функция КВАДРОТКЛ). (функция КВАДРОТКЛ).Вычислим размах прогнозного интервала для индивидуальных значений, используя формулу: 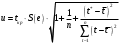 . .При 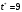 получим получим 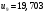 и определим границы доверительного интервала: и определим границы доверительного интервала: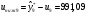 ; ; 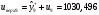 . .Таким образом, с надежностью 70% можно утверждать, что социально-экономический показатель по Алтайскому краю Y5 в следующем (2018) году будут составлять от 991,09 до 1030,496. 6.Представить графически фактические значения показателя, результаты моделирования и прогнозирования. Для построения чертежа используем Мастер диаграмм (точечная) – покажем исходные данные. Затем с помощью опции «Добавить линию тренда…» построим линию модели: тип → линейная; параметры → показывать уравнение на диаграмме. Покажем на графике результаты прогнозирования. Для этого в опции Исходные данные добавим ряды: Имя → прогноз; значения Х → t*; значения Y → 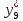 ; ;Имя → нижние границы; значения Х → t*; значения Y → uниж9; Имя → верхние границы; значения Х → t*; значения Y → uверх9. 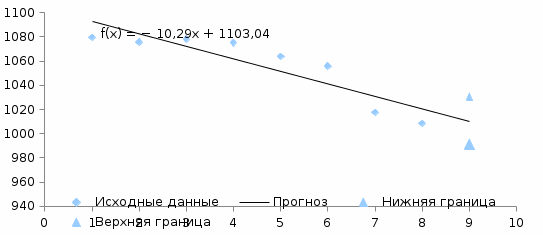 7.Провести расчет параметров логарифмического, полиномиального (полином 2-й степени), степенного, экспоненциального и гиперболического трендов. На основании графического изображения и значения индекса детерминации выбрать наиболее подходящий вид тренда. Для построения чертежа используем Мастер диаграмм (точечная) – покажем исходные данные. Затем с помощью опции «Добавить линию тренда…» построим линии модели: Логарифмический тренд 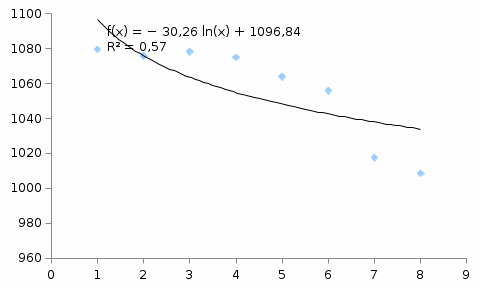 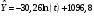 ; ;  Степенной тренд   ; ;  Полиноминальный тренд   ; ;  Экспоненциальный тренд   ; ;  Гиперболический тренд Для построения гиперболического тренда выполняем линеаризацию переменной t: T=1/t. Получаем:    Уравнение гиперболического тренда имеет вид:   Показательный тренд Для построения гиперболического тренда выполняем линеаризацию переменной Y:  . .Получаем:    Уравнение показательного тренда имеет вид:  или или  У полученных уравнений трендов наибольший коэффициент детерминации имеет полиноминальный тренд:  ; ;  . Следовательно, для анализа данного динамического ряда полиноминальный тренд является наиболее подходящим. . Следовательно, для анализа данного динамического ряда полиноминальный тренд является наиболее подходящим.8.Составить уравнения нелинейной регрессии (гиперболической; степенной; показательной, полиномиальной) По каждой модели: привести графики построенных уравнений регрессии; найти средние относительные ошибки аппроксимации, коэффициенты детерминации и коэффициенты эластичности. По этим характеристикам сравнить нелинейные модели между собой и сделать вывод. Составляем уравнения нелинейных регрессий на основании уравнений трендов, полученных в предыдущем пункте. Гиперболическая регрессия    Степенная регрессия  ; ;   Полиноминальная регрессия  ; ;   Показательная регрессия  или или   Находим средние ошибки аппроксимации для каждой модели по формуле:   Таким образом, наименьшая ошибка аппроксимации у полиноминальной регрессии:  Находим критерии Фишера для каждой модели по формуле:   Из всех моделей не значима только гиперболическая. Наибольший критерий Фишера у полиноминальной модели. На основании проведенного анализа было установлено, что у полиноминальной модели наименьшая средняя ошибка аппроксимации и наибольшие значения критерия Фишера и коэффициента детерминации. Следовательно, полиноминальная модель  признается наилучшей. признается наилучшей. 9.Лучшую нелинейную модель сравнить с лучшей линейной моделью. На основании проведенного ранее анализа линейная трендовая модель не является адекватной реальному ряду наблюдений, для построения прогнозных оценок лучше использовать полиноминальную модель. 10.С помощью лучшей нелинейной модели осуществить точечное прогнозирование рассматриваемого показателя на год вперед. Сопоставить полученный результат с доверительным прогнозным интервалом, построенным при использовании линейной модели. Выполняем прогноз на основе полиноминальной модели (t=9):  Для интервального прогноза составляем таблицу промежуточных вычислений: 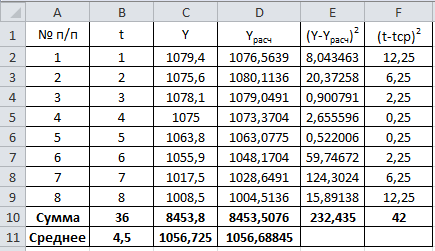 Дисперсия ошибки уравнения: 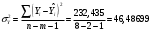 Стандартная ошибка уравнения полиноминальной регрессии: 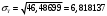 . . Критическое значение  найдено для уровня значимости =5% и числа степеней свободы 5 (функция СТЬЮДРАСПОБР). найдено для уровня значимости =5% и числа степеней свободы 5 (функция СТЬЮДРАСПОБР).Вычислим размах прогнозного интервала для индивидуальных значений, используя формулу: 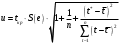 . .При 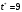 получим получим 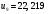 и определим границы доверительного интервала: и определим границы доверительного интервала: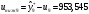 ; ;  . .Таким образом, с надежностью 95% можно утверждать, что социально-экономический показатель по Алтайскому краю Y5 в следующем (2018) году будут составлять от 953,545 до 997,983. У нелинейной регрессии значение ошибки прогноза больше, чем у линейной, но не намного, следовательно границы доверительных интервалов у полиноминальной регрессии превышают те же границы у линейной. Список литературыОрлова И.В. Экономико-математические методы и модели: компьютерное моделирование: учеб. пособие/ И. В. Орлова, В. А. Половников. – 3-е изд., перераб. и доп. – М.: Вузовский учебник: Инфра-М, 2014. – 389 с. (ЭБС Znanium.com). Гармаш А.Н. Математические методы в управлении: учеб. пособие/ А. Н. Гармаш, И. В. Орлова. – М.: Вузовский учебник: Инфра-М, 2012. – 272 с. (ЭБС Znanium.com). Короткова Т.Л. Исследования в менеджменте: учеб. пособие/ Т. Л. Короткова. – М.: Курс: Инфра-М, 2013. – 256 с. (ЭБС Znanium.com). Лабскер Л.Г. Вероятностное моделирование в финансово-экономической области: учеб. пособие/ Л. Г. Лабскер. – 2-е изд. – М.: Инфра-М, 2017. – 172 с. (ЭБС Znanium.com). 1 2 | |||||||||||||||||||||||||||||||||||||||||||||||||||