задачи по математика. Задачи. Задача 1 3 Задача 2 5 Задача 3 10 Задача 4 12 Задача 1 Условие x 1 3x 2 9, (2)

• Название: Задача 1 3 Задача 2 5 Задача 3 10 Задача 4 12 Задача 1 Условие x 1 3x 2 9, (2)
• Анкор: задачи по математика
• Дата: 03.12.2022
• Размер: 244.13 Kb.
• Имя файла: Задачи.docx
• Тип: Задача; #826130
• страница: 4 из 4

Определим ранг основной системы системы.

0 2 28 6 9 4 29 3

Выделенный минор имеет наивысший порядок (из возможных миноров) и отличен от нуля. Ранг этой системы равен rangA=2.
Определим ранг расширенной системы системы.

0 2 28 6 2 9 4 29 3 -5

Ранг этой системы равен rangB=2.
rang(A) = rang(B) = 2. Поскольку ранг основной матрицы равен рангу расширенной, то система является совместной.
Этот минор является базисным. В него вошли коэффициенты при неизвестных x₁,x₂, значит, неизвестные x₁,x₂ – зависимые (базисные), а x₃,x₄ – свободные.

Преобразуем матрицу, оставляя слева только базисный минор.

0 2 2 -28 -6 9 4 -5 -29 -3

Система с коэффициентами этой матрицы эквивалентна исходной системе и имеет вид:

2x₂ = 2 - 28x₃ - 6x₄

9x₁ + 4x₂ = - 5 - 29x₃ - 3x₄

Получили соотношения, выражающие зависимые переменные x₁,x₂ через свободные x₃,x₄, то есть нашли общее решение:

x₂ = 1 - 14x₃ - 3x₄

x₁ = - 1 + 3x₃ + x₄

Система является совместной.

Решим систему уравнений методом Гаусса.

Запишем систему в виде расширенной матрицы:

9 4 29 3 1 0 -3 -1 5 2 13 1 2 1 8 1 4 -1 -2 1

-5 -1 -3 -1 3

Для удобства вычислений поменяем строки местами:

1 0 -3 -1 2 1 8 1 4 -1 -2 1 5 2 13 1 9 4 29 3

-1 -1 3 -3 -5

Умножим 2-ю строку на (2). Умножим 3-ю строку на (-1). Добавим 3-ю строку к 2-й:

0 -1 -14 -3 0 3 18 1 4 -1 -2 1 5 2 13 1 9 4 29 3

-1 -5 3 -3 -5

Умножим 3-ю строку на (5). Умножим 4-ю строку на (-4). Добавим 4-ю строку к 3-й:

0 -1 -14 -3 0 3 18 1 0 -13 -62 1 5 2 13 1 9 4 29 3

-1 -5 27 -3 -5

Умножим 4-ю строку на (9). Умножим 5-ю строку на (-5). Добавим 5-ю строку к 4-й:

0 -1 -14 -3 0 3 18 1 0 -13 -62 1 0 -2 -28 -6 9 4 29 3

-1 -5 27 -2 -5

Умножим 1-ю строку на (3). Добавим 2-ю строку к 1-й:

0 0 -24 -8 0 3 18 1 0 -13 -62 1 0 -2 -28 -6 9 4 29 3

-8 -5 27 -2 -5

Умножим 2-ю строку на (13). Умножим 3-ю строку на (3). Добавим 3-ю строку к 2-й:

0 0 -24 -8 0 0 48 16 0 -13 -62 1 0 -2 -28 -6 9 4 29 3

-8 16 27 -2 -5

Умножим 3-ю строку на (2). Умножим 4-ю строку на (-13). Добавим 4-ю строку к 3-й:

0 0 -24 -8 0 0 48 16 0 0 240 80 0 -2 -28 -6 9 4 29 3

-8 16 80 -2 -5

Умножим 1-ю строку на (2). Добавим 2-ю строку к 1-й:

0 0 0 0 0 0 48 16 0 0 240 80 0 -2 -28 -6 9 4 29 3

0 16 80 -2 -5

Умножим 2-ю строку на (5). Умножим 3-ю строку на (-1). Добавим 3-ю строку к 2-й:

0 0 0 0 0 0 0 0 0 0 240 80 0 -2 -28 -6 9 4 29 3

0 0 80 -2 -5

Для удобства вычислений поменяем строки местами:

0 0 0 0 0 0 0 0 0 0 240 80 0 -2 -28 -6 9 4 29 3

0 0 80 -2 -5

Теперь исходную систему можно записать так:

x₃ = [80 - (80x₄)]/240

x₂ = [-2 - ( - 28x₃ - 6x₄)]/(-2)

x₁ = [-5 - (4x₂ + 29x₃ + 3x₄)]/9

Необходимо переменную x₄ принять в качестве свободной переменной и через нее выразить остальные переменные.
Приравняем переменную x₄ к 0

Из 3-й строки выражаем x₃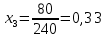



Из 4-й строки выражаем x₂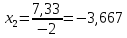


Из 5-й строки выражаем x₁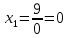



Находим х₄ из первой строки

0+4·-3,667+29·0,33+5=-3х₄

х₄= 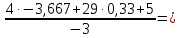0,032

Ответ:х₃= 0,33, х₂=-3,667,х₁=1, х₄=0,032