задачи по математика. Задачи. Задача 1 3 Задача 2 5 Задача 3 10 Задача 4 12 Задача 1 Условие x 1 3x 2 9, (2)

• Название: Задача 1 3 Задача 2 5 Задача 3 10 Задача 4 12 Задача 1 Условие x 1 3x 2 9, (2)
• Анкор: задачи по математика
• Дата: 03.12.2022
• Размер: 244.13 Kb.
• Имя файла: Задачи.docx
• Тип: Задача; #826130
• страница: 2 из 4

Задача 3

Условие

Исследовать совместность систему уравнений методом Кронекера-Капелли. Если уравнения совместны, решить их методом Гаусса.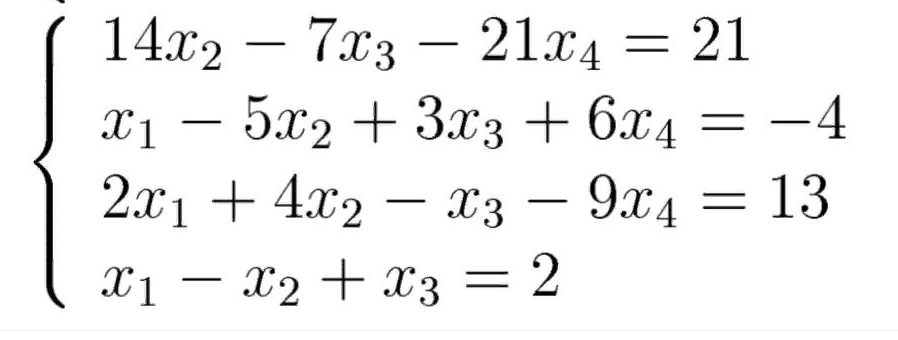



Решение

Исследуем эту систему по теореме Кронекера-Капелли.
Выпишем расширенную и основную матрицы.

Таблица 3.1

0 14 -7 -21 21 1 -5 3 6 -4 2 4 -1 -9 13 1 -1 1 0 2 x1 x2 x3 x4

Здесь матрица А выделена жирным шрифтом.
Приведем матрицу к треугольному виду. Будем работать только со строками, так как умножение строки матрицы на число, отличное от нуля, и прибавление к другой строке для системы означает умножение уравнения на это же число и сложение с другим уравнением, что не меняет решения системы.

Умножим 2-ую строку на (-2). Добавим 3-ую строку к 2-ой:

Таблица 3.2

14 -7 -21 21 0 14 -7 -21 21 2 4 -1 -9 13 1 -1 1 0 2

В матрице B 1-ая и 2-ая строки пропорциональны, следовательно, одну из них, например 1-ю, можно вычеркнуть. Это равносильно вычеркиванию 1-го уравнения системы, так как оно является следствием 2-го.

Таблица 3.3

0 14 -7 -21 21 2 4 -1 -9 13 1 -1 1 0 2

Умножим 2-ую строку на (-1). Умножим 3-ую строку на (2). Добавим 3-ую строку к 2-ой:

Таблица 3.4

0 14 -7 -21 21 0 -6 3 9 -9 1 -1 1 0 2

В матрице B 1-ая и 2-ая строки пропорциональны, следовательно, одну из них, например 1-ю, можно вычеркнуть. Это равносильно вычеркиванию 1-го уравнения системы, так как оно является следствием 2-го.

Таблица 3.5

0 -6 3 9 -9 1 -1 1 0 2

Определим ранг основной системы системы.

Таблица 3.6

0 -6 3 9 1 -1 1 0

Выделенный минор имеет наивысший порядок (из возможных миноров) и отличен от нуля. Ранг этой системы равен rangA=2.
Определим ранг расширенной системы системы.

Таблица 3.7

0 -6 3 9 -9 1 -1 1 0 2

Ранг этой системы равен rangB=2.

rang(A) = rang(B) = 2. Поскольку ранг основной матрицы равен рангу расширенной, то система является совместной.
Этот минор является базисным. В него вошли коэффициенты при неизвестных x₁,x₂, значит, неизвестные x₁,x₂ – зависимые (базисные), а x₃,x₄ – свободные.

Преобразуем матрицу, оставляя слева только базисный минор.

Таблица 3.8

0 -6 -9 -3 -9 1 -1 2 -1 0

Система с коэффициентами этой матрицы эквивалентна исходной системе и имеет вид:

- 6x₂ = - 9 - 3x₃ - 9x₄

x₁ - x₂ = 2 - x₃

Получили соотношения, выражающие зависимые переменные x₁,x₂ через свободные x₃,x₄, то есть нашли общее решение:
x₂ = ³/₂ + ¹/₂x₃ + ³/₂x₄
x₁ = ⁷/₂ - ¹/₂x₃ + ³/₂x₄

Ответ: придавая свободным неизвестным любые значения, получим сколько угодно частных решений. Система является неопределенной, т.к. имеет более одного решения. Система является несовместной.