Э-математическая модель. Задача 1 Дано Производственная функция вида y min K 3L. Определить
 Скачать 86 Kb. Скачать 86 Kb.
|
|
Задача №1 Дано: Производственная функция вида: y = min {K; 3L}. Определить: Графически построить изокванты данной функции. Вывести на её основе уравнения функций производственных затрат и определить их характеристики (средние и предельные затраты). Решение Данная функция относится к классу функций с взаимодополняемыми ресурсами. Изокванты такой функции в пространстве двух ресурсов представляют собой прямые углы. Для графического построения изоквант данной функции необходимо определить их вершины, т.е. точки, в которых достигаются минимальные затраты ресурсов, обеспечивающие определенные объемы производства. Исходя из условий задачи, минимум затрат обоих ресурсов при производстве продукции в объеме y будет достигнут, когда выполняется равенство: y =K = 3L В этом случае оба ресурса используются полностью, избытка того или иного ресурса не возникает. Следовательно: K/L = 3 Иными словами, ресурсы будут использоваться наиболее эффективно, если они используются в соотношении 3:1 (на 3 единиц капитала 1 единица труда). Все точки в пространстве двух ресурсов, координаты которых соотносятся как 3:1, будут являться вершинами углов изоквант.        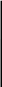   K L 1 2 3 6 0 Функции затрат ресурсов будут иметь вид: K = y L = y/3 Средние затраты ресурсов: qK = y/y = 1 qL = y/3y = 1/3 Предельные затраты: hK = d(y)/dy = 1. hL = d(y/3)/dy = 1/3. Задача №2 Дано: Функция полезности потребителя имеет вид: u (x, y) = 2xy Цены товаров: Px = 6 д.е., Py = 3 д.е. Доход потребителя составляет: I = 36 д.е. Запишите задачу потребителя и определите уровень полезности, достигаемый потребителем в точке оптимума. Решение: Запишем задачу потребительского выбора: 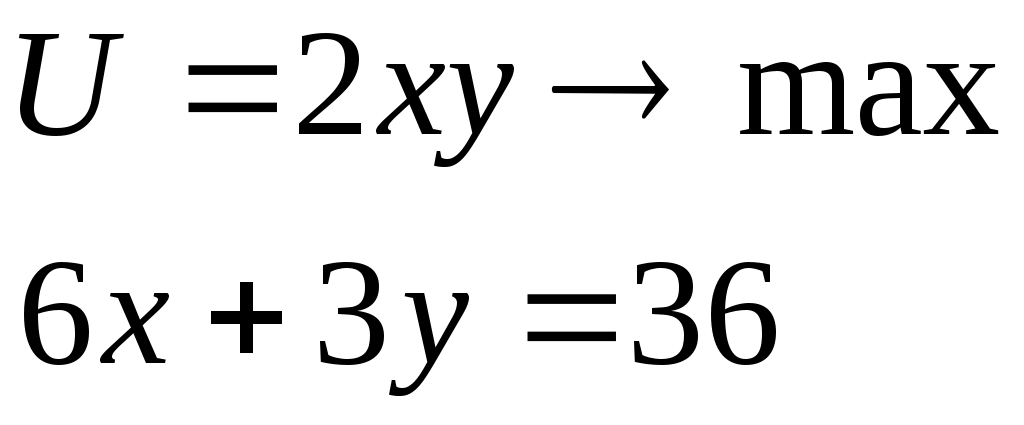 В условиях задачи предельные полезности товаров, представляющие собой частные производные функции полезности, равны: MUx=2y MUy=2x Тогда условия первого порядка решения задачи потребителя приобретают следующий вид: 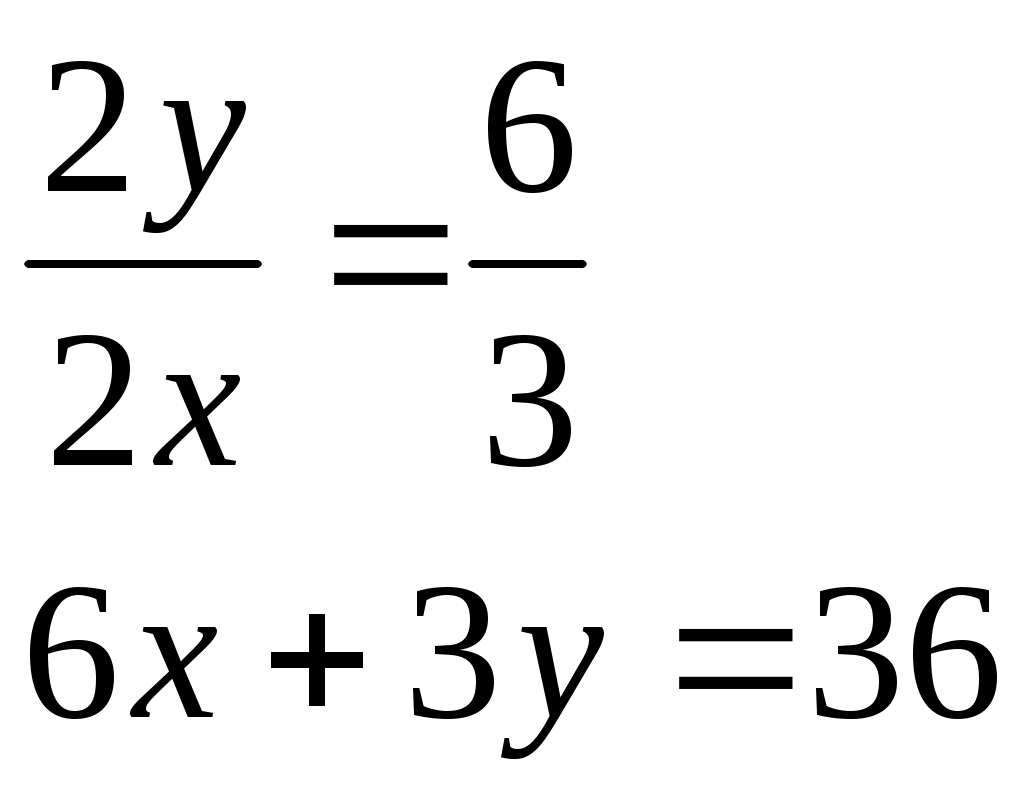 или 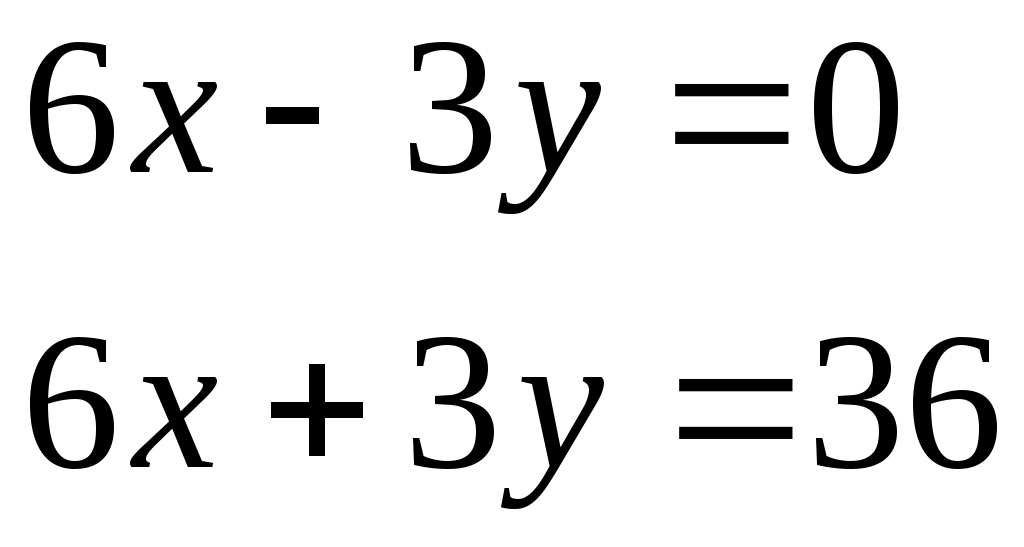 Следовательно, мы можем определить x1 и x2 – объем потребления каждого вида товара, обеспечивающий потребителю наибольший уровень полезности: x1 = 3 x2 = 6 Тогда уровень полезности, достигаемый потребителем в точке оптимума, составит: u = 2 x y = 2*3*6 = 36 единиц. Задача №3 Дано: Взаимосвязи отраслей в двухотраслевой экономике отражены в таблице (млрд.руб):
Определить: Коэффициенты прямых затрат (коэффициенты матрицы А) Записать основные уравнения модели межотраслевого баланса Решение: Коэффициенты прямых затрат (величины aij)в модели межотраслевого баланса рассчитываются следующим образом: aij = xij / Xj , i, j = 1, 2,...,n. Основные уравнения модели межотраслевого баланса имеют вид: 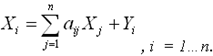 В условиях задачи: х11=30, х12=30, х21=20, х22=10 Y1=40, Y2=30 Z1=50, Z2=20 X1= х11+ х12+ Y1=30+30+40=100 или X1= х11+ х21+ Z1=20+10+30=60 Тогда: a11 = 30/100=0.3; a12 = 30/60=0.5; a21 = 20/100=0.2; a22 = 10/60=0.167; Тогда основные уравнения модели МОБ принимают вид: 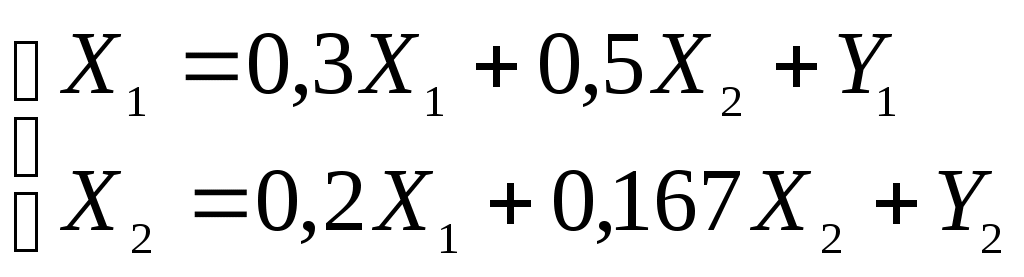 Задача №4 Предположим, что в маленьком городе есть два оператора мобильной связи. Фирма А оценивает, что она может увеличить прибыль на 1000 д.е. в месяц, если снизит цены на услуги связи на 10% при условии, что ее соперник сохранит свою цену. С другой стороны, если ее конкурент ответит понижением цены, то она потеряет 500 д.е. в месяц. Если фирма сохраняет свою цену, то ее прибыль не меняется, пока конкурент также удерживает прежнюю цену. Если же конкурент понизит цену, то она потеряет 500 д.е. в месяц. Составьте платежную матрицу для фирмы А и укажите доминантную стратегию для нее, если таковая существует. Решение: Составим платежную матрицу (матрицу выигрышей) для фирмы А. Для этого внесем в таблицу размер изменения прибыли фирмы при различных вариантах действий фирмы А и конкурента.
Матрица игры: 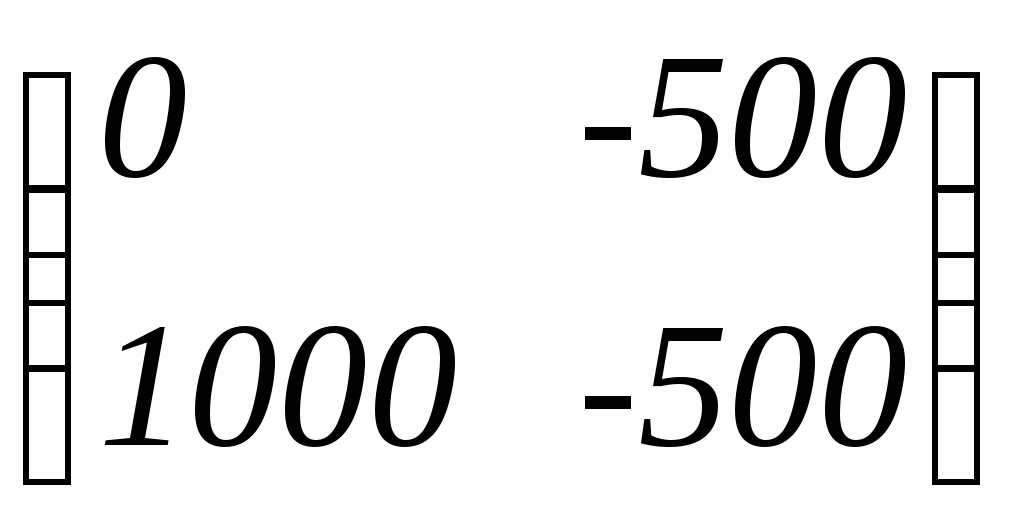 Для фирмы А доминантная стратегия «снизить цену», поскольку все элементы второй строки больше или равны элементов первой строки. |
