Термодинамика. Термодинамика 1. Задача 1 Газовая смесь задана процентным составом компонентов смеси со
 Скачать 1.09 Mb. Скачать 1.09 Mb.
|
|
Задача №1 Газовая смесь задана процентным составом компонентов смеси СО2, Н2, СО, Н2О, О2, N2, SO2 в массовых долях (табл. 1). Давление смеси равно Рсм (табл. 1, строка 8). Объем смеси равен Vсм (табл. 1, строка 9). Температура смеси равна tсм (табл. 1, строка 10). В интервале температур t (табл. 1, строка 11) смесь нагревается. Данные для соответствующего варианта берутся из табл. 1. Определить: 1. Объемный состав смеси. 2. Газовые постоянные компонентов Ri и смеси Rсм, кДж/(кг∙К). 3. Среднюю молярную массу смеси µсм через объемные и массовые доли, кг/кмоль. 4. Парциальные давления компонентов через объемные и массовые доли. 5. Массу смеси Мсм, кг и массы компонентов Мi, кг. 6. Парциальные объемы компонентов Vi, м3. 7. Плотности компонентов и смеси при нормальных физических условиях через объемные и массовые доли. 8. Массовые теплоемкости с, кДж/(кг К) при рсм=соnst; Vсм=const; для температуры смеси tсм, °С, (строка 10). 9. Количество теплоты, необходимое для нагревания (охлаждения) 7 кг смеси в интервале температур (строка 11) при р=const. Таблица 1
Решение: 1. Определение объемного состава смеси Процентный состав компонентов смеси изобразим на диаграмме (рис. 1):  Рисунок 1 – Диаграмма компонентов смеси (в процентах) Вычисление объемной доли Определим объемную долю компонентов (табл. 2): Таблица 2
2. Вычисление средней молярной массы смеси через объемные и массовые доли Определим средний молекулярный вес смеси (через объемные доли):  где 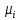 - молярная масса компонента смеси, в данном случае - молярная масса компонента смеси, в данном случае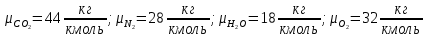 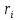 - объемная доля компонента смеси (см. табл. 2): - объемная доля компонента смеси (см. табл. 2):Имеем:  Найдем массовые доли каждого компонента смеси газов: Используем формулу:  Имеем:   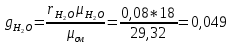  Сделаем проверку: 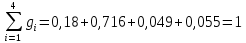 Определим средний молекулярный вес смеси (через массовые доли): 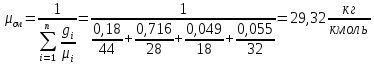 Вывод: получен тот же результат, что и в расчетах, проведенных выше. 3. Вычисление газовых постоянных компонентов и смеси Газовые постоянные компонентов смеси:  Имеем:     Газовая постоянная смеси: 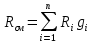 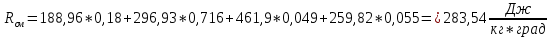 Сделаем проверку:  Вывод: расчет проведен правильно. 4. Вычисление парциального давления компонентов через объемные и массовые доли Определим парциальные давления через объемные доли: По условию Pсм = 0,95 МПа. 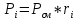 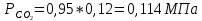 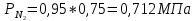 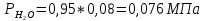  Определим парциальные давления через массовые доли:  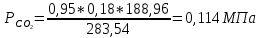 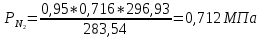   Вывод: результаты получились одинаковыми. 5. Вычисление массы смеси и массы компонентов Определение массы смеси:  где: Рсм = 0,95 МПа = 0,95·106 Па; Vсм =2 м3; Rсм = 283,54 Дж/(кг·град) =0,28354 кДж/(кг·град) Т = 2000+273=2273 К. Подставляем: 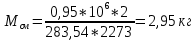 Определение массы компонентов: 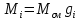     Создадим диаграмму компонентов смеси (в кг) рис. 2. Она отличается от диаграммы компонентов смеси (в %) (см. рис.1). Это и понятно. Водород – очень легкий газ и не может обладать большой массой, сколько бы его не было в составе смеси. 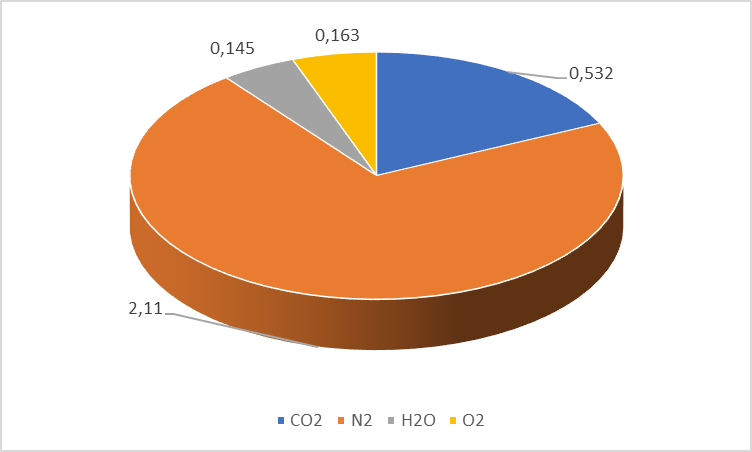 Рисунок 2 – Диаграмма компонентов смеси (в кг) Проверка: 0,532+2,11+0,145+0,163=2,95 кг 6. Вычисление парциальных объемов компонентов 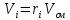  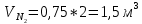 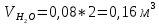 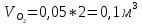 Проверка: 0,24+1,5+0,16+0,1=2 м3 7. Вычисление плотности компонентов и смеси при нормальных физических условиях через объемные и массовые доли Вычисление плотности компонентов:   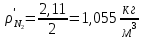 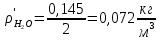 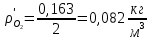 Вычисление плотности смеси при заданных условиях: 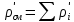 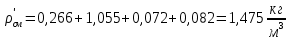 Проверка:  Вывод: вычисления произведены верно. 8. Вычисление массовых теплоемкостей Вычислим массовые теплоемкости с, кДж/(кг*К) при рсм=соnst; Vсм=const; для температуры смеси tсм=2000°С. Для расчетов воспользуемся таблицей. Таблица 2 – Удельная изобарная теплоемкость элементов cp, Дж/(кг·К)
Замечание: В таблице справочника нет значений для температуры 2000°С, поэтому нам пришлось прибегнуть к экстраполяции. Массовая теплоемкость при постоянном давлении при tсм=2000°С: 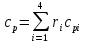  Массовая теплоемкость при постоянном объеме при tсм=2000°С: Воспользуемся законом Майера: 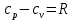 Тогда  Получаем: 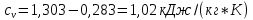 Ответ: cp = 1,303 кДж/(кг·К); cv = 1,02 кДж/(кг·К); 9. Вычисление количества теплоты Вычислим затраты тепла на нагревание в процессе при постоянном давлении (здесь мы взяли ср при 2000°С): 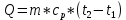 где m = 7 кг; ср = 1,303 кДж/(кг·К) t1 = 200°C t2 = 900°C Подставляя данные в формулу, получаем:  Ответ: 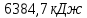 Задача №2 Определить изменение энтропии ∆S для М кг азота в политропном процессе при изменении температуры от t1 до t2. Показатель политропы равен n. Теплоемкость азота считать постоянной, Ср=1,06 кДж/(кг*К). Данные для соответствующего варианта берутся из табл. 3. Таблица 3
Решение: Второй закон термодинамики устанавливает направление самопроизвольных тепловых процессов в природе и определяет условия превращения тепла в работу. Он утверждает, что тепло в природе самопроизвольно переходит только от тел более нагретых к менее нагретым. Средняя удельная изохорная теплоёмкость азота cv в данном диапазоне температур найдется как 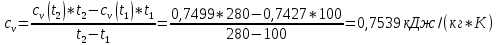 Показатель адиабаты 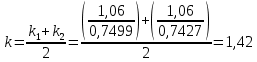 Важнейшим параметром состояния вещества является энтропия S. Изменение энтропии в политропном процессе:   Ответ: -1,0873 кДж/К Задача №3 Для идеализированного цикла двигателя внутреннего сгорания, заданного значениями параметров, приведенных в таблице 4, определить давление, удельный объем и температуру во всех характерных точках цикла; работу и теплоту за цикл, а также термический кпд цикла. Известны параметры в начальной точке процесса р1, и t1, степень сжатия  , степень повышения давления , степень повышения давления 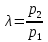 bстепень предварительного расширения bстепень предварительного расширения 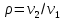 . В качестве рабочего тела принять 1 кг воздуха. Зависимость теплоемкости от температуры считать линейной и рассчитать по интерполяционным формулам, приведенным в [9, табл. 5]. Изобразить цикл в произвольном масштабе на координатах p-v и T-s. . В качестве рабочего тела принять 1 кг воздуха. Зависимость теплоемкости от температуры считать линейной и рассчитать по интерполяционным формулам, приведенным в [9, табл. 5]. Изобразить цикл в произвольном масштабе на координатах p-v и T-s.Таблица 4
Решение: Определим параметры в точке 1: Начальный удельный объем определяем из уравнения состояния  Определим параметры в точке 2: Так как степень сжатия  , то: , то: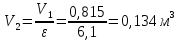 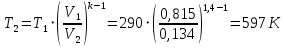  Параметры точки 3: Из соотношения параметров в изохорном процессе получаем:    Параметры точки 4: Из соотношения параметров в изобарном процессе получаем: 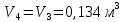 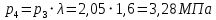  Параметры в точке 5: 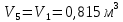 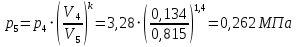 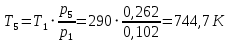 Работа цикла может быть определена как разность между работой расширения и работой сжатия: 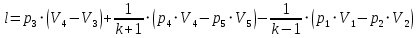  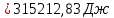 Количество подведенной теплоты: Количество подведенной теплоты: 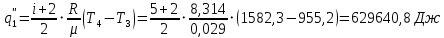 Количество отведенной теплоты:  Полезно использованная теплота:  Термический КПД цикла равен: 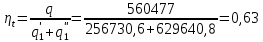 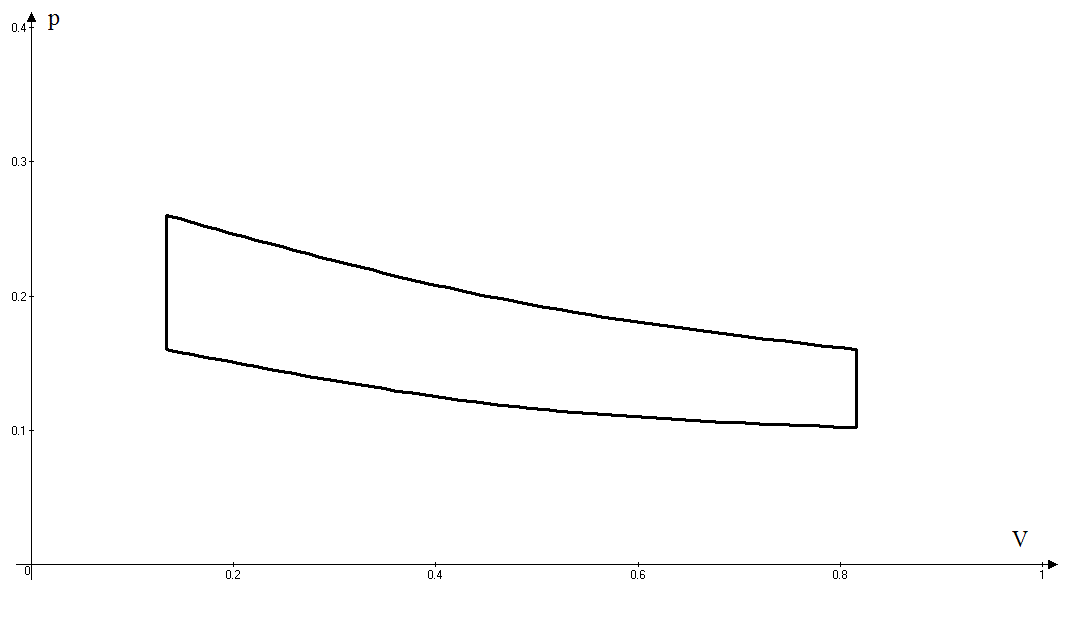  Рис. 1. Диаграммы в p - V и T – s Задача №4 Паротурбинная установка работает по теоретическому циклу Ренкина. Давление и температура водяного пара на выходе из парогенератора (перед турбиной): Р1 и t1 давление пара после турбины (в конденсаторе) Р2: Определить термический коэффициент полезного действия цикла ηt и теоретический удельный расход пара d, кг/(кВт*ч) при следующих условиях работы установки: Паротурбинная установка работает по теоретическому циклу Ренкина. Давление и температура водяного пара на выходе из парогенератора (перед турбиной): Р1 и t1 давление пара после турбины (в конденсаторе) Р2: Определить термический коэффициент полезного действия цикла ηt и теоретический удельный расход пара d, кг/(кВт*ч) при следующих условиях работы установки: I — p1, t1 и p2 II — p1, t1 III — p1, t1и p2 Сделать вывод о влиянии уровня начальных параметров состояния пара и давления пара после турбины на значения термического КПД цикла Ренкина и удельного расхода пара. К решению задачи приложить принципиальную схему паротурбинной установки, изображение цикла Ренкина в координатах р-υ и T-s, также изображение процесса расширения пара в турбине в диаграмме h-s. Таблица 5
Таблица 6
Решение  Рис.2. Принципиальная схема паросиловой установки.  Рис. 3. Цикл Ренкина паросиловой установки: а) в Вариант I Дано: Строим процесс адиабатного расширения пара в турбине в По Опускаясь по адиабате По таблице свойств насыщенного водяного пара (по давлениям) при давлении Термический  (1) (1)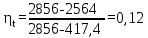 Теоретический удельный расход пара на  (2) (2)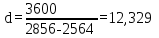 Вариант II Дано: Строим процесс адиабатного расширения пара в турбине в Термический  Теоретический удельный расход пара на 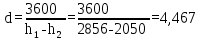 Вариант III Дано: Удельные энтальпии пара на входе и выходе из турбины, а также на выходе из конденсатора: Термический 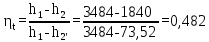 Теоретический удельный расход пара на  Вывод о влиянии начальных параметров пара при поступлении в турбину С повышением начальных параметров пара: 1 - термический 2 - количество пара 3 - идеальный цикл Ренкина в паросиловой установке по сравнению с идеальным циклом Карно: - делает установку компактнее, так как насос по размерам значительно меньше компрессора; - делает установку экономичнее, так как мощность насоса во много раз меньше мощности компрессора.  Рис.4. Определение параметров пара по Задача №5 Через плоскую стенку толщиной δ, длиной l и площадью F (или через цилиндрическую стенку с наружным диаметром d2, толщиной δ и длиной l) передается тепловой поток при стационарном режиме. Коэффициент теплопроводности и стенки λ, температура поверхности стенки: с одной стороны tс1, с другой стороны tс2. Определить поверхностную плотность теплового потока q для плоской стенки или линейную плотность теплового потока q1 для цилиндрической стенки, мощность теплового потока Q через стенку. Изобразить схематично график распределения температур по толщине стенки. Таблица 7
Решение:  Рис.5. Стационарное температурное поле в цилиндрической стенке Тепловой поток, проходящий через цилиндрическую стенку длиной ℓ, найдем по закону Фурье  Поверхностная плотность теплового потока рассчитывается по формуле 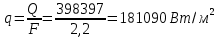 Ответ: 181090 Вт/м2 Задача №6 Газовая смесь состоит из нескольких компонентов, содержанке которых в смеси задано в процентах по объему (табл. 8). Определить: 1) кажущуюся молекулярную массу смеси; 2) газовую постоянную смеси; 3) средние мольную, объемную и массовую теплоемкости смеси при постоянном давлении в пределах температур от t1 до t2 (табл.9). При решении этой задачи и последующих задач для всех исходных и итоговых величин, кроме относительных, (безразмерных) величин, должны быть указаны единицы измерения. Дано: CO2=20% O2=5% N2=75% t1=1342 C° t2=2143 C° Решение: 1. Вычислим кажущуюся молекулярную массу смеси: 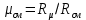 Эта формула недостаточно удобная, так как нам не дана газовая постоянная смеси, поэтому мы воспользуемся другой. Запишем уравнение состояния для массы газа mi:  или, с учетом или, с учетом 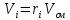  Заменим 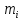 и и 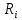 на: на: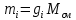 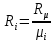 Получим: 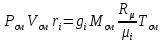 Если записать выражения для каждого компонента смеси и просуммировать, то получим:  с учетом того, что: 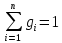 Тогда 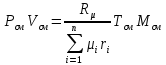 Таким образом 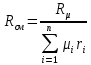 Выполнив подстановку в формулу 1, получим, что 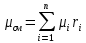 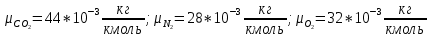 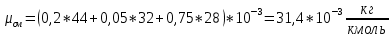 2. Вычислим газовую постоянную смеси. Для этого воспользуемся формулой, выведенной в предыдущем пункте: 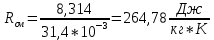 3. Вычислим средние мольную, объемную и массовую теплоемкости смеси при постоянном давлении в интервале температур от 1342 С до 2143 С. Определим по таблице средние мольные теплоемкости при p=const для компонентов смеси для верхнего и нижнего предела температур: Для t1=1342 C: 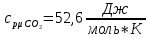  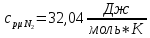 Для t2=2143 C: 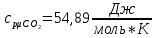 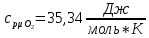 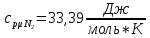 Воспользуемся формулой для определения средней мольной теплоемкости смеси в интервале температур: 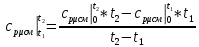 Где  Найдем средние мольные теплоемкости смеси для t1и t2:   Подставим значения в формулу:  Зная среднюю мольную теплоемкость смеси несложно получить средние объёмную и массовую теплоемкости по известным зависимостям: 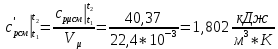  Задача №7 Задано топливо и паропроизводительность котельного агрегата D. Определить состав рабочей массы топлива и его низшую теплоту сгорания, способ сжигания топлива, тип топки, значение коэффициента избытка воздуха в топке αт; найти теоретическое количество воздуха, необходимое для сгорания 1 кг (1 м3) топлива, и объем продуктов сгорания при αт. Указание. Состав, рекомендации по выбору типа топки и коэффициента избытка воздуха приведены в прилож. Дано: Вид топлива – Челябинский уголь БЗ (бурый) D = 160 т/ч; = 0,15; tух = 130 С Решение: Для определения элементарного состава и низшей теплоты сгорания топлива, а также для выбора типа топки и коэффициента избытка воздуха т используем согласно рекомендациям Приложения. Состав рабочей массы топлива по Приложению: 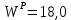 %; %;  %; %;  %; %; %; %; 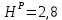 %; Np = 0,9 %; %; Np = 0,9 %;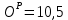 %; %;  мДж/кг; Vг = 45 %. мДж/кг; Vг = 45 %.Тип топки согласно Приложению 7 – пылеугольная. Из Приложения 8 находим коэффициент избытка воздуха т = 1,20. Коэффициент избытка воздуха за установкой  . .Теоретическое необходимое количество воздуха: 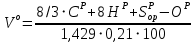 , ,  где 1,429 – плотность кислорода при нормальных условиях, кг/м3; 0,21 – объемная доля кислорода в воздухе; СР, НР, SPop, OP – весовые доли углерода, водорода, серы, кислорода в топливе, %, соответственно  . .Объем продуктов сгорания 1 кг топлива 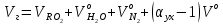 , ,где 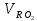 – объем трехатомных газов; – объем трехатомных газов; . .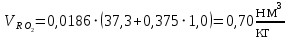 . .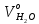 – объём водяных паров; – объём водяных паров; , нм3/кг. , нм3/кг.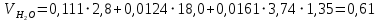 нм3/кг. нм3/кг.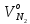 – теоретический объем азота; – теоретический объем азота;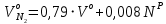 , нм3/кг , нм3/кг нм3/кг. нм3/кг.Тогда  нм3/кг. нм3/кг.Находим энтальпию уходящих газов 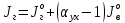 где 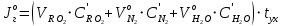 – энтальпия продуктов сгорания при ух = 1 и tух; – энтальпия продуктов сгорания при ух = 1 и tух;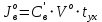 – энтальпия воздуха при ух = 1 и tух; – энтальпия воздуха при ух = 1 и tух;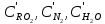 – средние объёмные теплоемкости (значения находим при tух = 130 С из табл. 9.2 [6]: – средние объёмные теплоемкости (значения находим при tух = 130 С из табл. 9.2 [6]: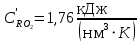 ; ;  = 1,31 = 1,31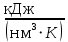 ; ; = 1,52 = 1,52 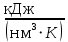 ; ; 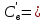 1,30 1,30 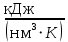 . .Тогда  кДж/кг. кДж/кг.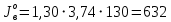 кДж/кг. кДж/кг.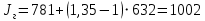 кДж/кг. кДж/кг.Ответ: с увеличением tух и ух энтальпия уходящих газов увеличивается. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
