ЭММ. Вариант 5. Задача 1 Графический метод решения задач линейногопрограммирования. Составить математическую модель по условию задачи
 Скачать 171.28 Kb. Скачать 171.28 Kb.
|
|
Содержание Задача 1 Графический метод решения задач линейногопрограммирования. 1. Составить математическую модель по условию задачи. 2. Решить задачу геометрическим способом. 3. Сделать выводы. Фирма производит два безалкогольных широко популярных напитка « Колокольчик» и «Буратино». Для производства 100 л. « Колокольчика требуется 4 ч работы оборудования, а для « Буратино» – 1 ч, а расход специального ингредиента на них на 100 л составляет 1 кг на Колокольчик и 4 кг на Буратино. Ежедневно в распоряжении фирмы 16 кг специального ингредиента и 24 ч работы оборудования. Прибыль от продажи 1 л» Колокольчика» составляет 4 руб., а « Буратино» – 9 руб. Определите ежедневный план производства напитков каждого вида, обеспечивающий максимальный доход от их продажи. Решение: Составим математическую модель данной задачи: Пусть X1 – количество « Колокольчиков»;Х2 – количество « Буратино», тогда как необходимо определить ежедневный план производства напитков каждого вида, обеспечивающий максимальный доход от их продажи, то целевая функция: F(Х1,Х2) = 4Х1+ 9Х2  мах махСистема ограничений: 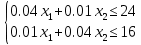 xj 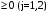 Графическое решение задачи: Необходимо найти максимальное значение целевой функции F = 4x1+9x2 → max, при системе ограничений: 0.04x1+0.01x2≤24, (1) 0.01x1+0.04x2≤16, (2) x1 ≥ 0, (3) x2 ≥ 0, (4) Шаг №1. Построим область допустимых решений, т.е. решим графически систему неравенств. Для этого построим каждую прямую и определим полуплоскости, заданные неравенствами (полуплоскости обозначены штрихом). 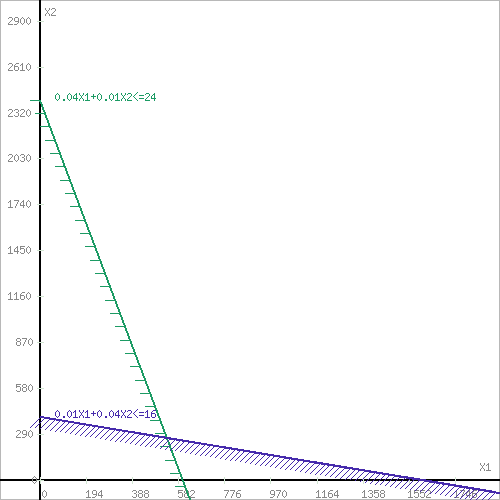 Шаг №2. Границы области допустимых решений. Пересечением полуплоскостей будет являться область, координаты точек которого удовлетворяют условию неравенствам системы ограничений задачи. Обозначим границы области многоугольника решений. 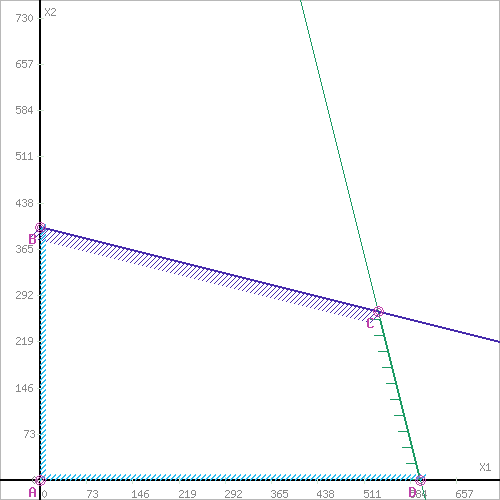 Шаг №3. Рассмотрим целевую функцию задачи F = 4x1+9x2 → max. Построим прямую, отвечающую значению функции F = 4x1+9x2 = 0. Вектор-градиент, составленный из коэффициентов целевой функции, указывает направление максимизации F(X). Начало вектора – точка (0; 0), конец – точка (4;9). Будем двигать эту прямую параллельным образом. Поскольку нас интересует максимальное решение, поэтому двигаем прямую до последнего касания обозначенной области. На графике эта прямая обозначена пунктирной линией. 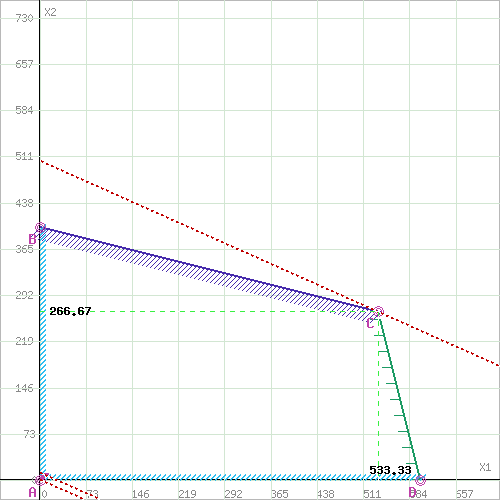 Прямая F(x) = const пересекает область в точке C. Так как точка C получена в результате пересечения прямых (1) и (2), то ее координаты удовлетворяют уравнениям этих прямых: 0.04x1+0.01x2=24 0.01x1+0.04x2=16 Решив систему уравнений, получим: x1 = 533.3333, x2 = 266.6667 Откуда найдем максимальное значение целевой функции: F(X) = 4*533.3333 + 9*266.6667 = 4533.3335 Вывод: максимальный доход от продажи составляет 4533.33 руб, при условии продажи 533 литров Колокольчика и 266 литровБуратино. Задача 2 Симплексный метод решения задач линейного программирования. Для изготовления четырех видов продукции используют три вида сырья. Запасы сырья, нормы его расхода и прибыль от реализации каждого продукта приведены в таблице. 1. Составить математическую модель задачи (сформировать систему ограничений и целевую функцию); 2. Привести систему ограничений к каноническому виду, обозначив и введя дополнительные переменные; 3. Построить симплексную таблицу и заполнить её первоначальным опорным планом; 4. Пользуясь алгоритмом симплексного метода, найти оптимальное решение задачи; 5. Сделать выводы. 6. Составить двойственную задачу, решить ее на основе теорем двойственности. Решение:
Решим прямую задачу линейного программирования симплексным методом, с использованием симплексной таблицы.Определим максимальное значение целевой функции F(X) = 40x1+60x2+80x3 при следующих условиях-ограничений. x1+4x2+3x3≤200 x1+x2+2x3≤80 x1+x2+2x3≤140 Для построения первого опорного плана систему неравенств приведем к системе уравнений путем введения дополнительных переменных (переход к канонической форме). В 1-м неравенстве смысла (≤) вводим базисную переменную x4. В 2-м неравенстве смысла (≤) вводим базисную переменную x5. В 3-м неравенстве смысла (≤) вводим базисную переменную x6. x1+4x2+3x3+x4 = 200 x1+x2+2x3+x5 = 80 x1+x2+2x3+x6 = 140 Матрица коэффициентов A = a(ij) этой системы уравнений имеет вид:
Базисные переменные это переменные, которые входят только в одно уравнение системы ограничений и притом с единичным коэффициентом. Решим систему уравнений относительно базисных переменных: x4, x5, x6 Полагая, что свободные переменные равны 0, получим первый опорный план: X0 = (0,0,0,200,80,140) Базисное решение называется допустимым, если оно неотрицательно.
Переходим к основному алгоритму симплекс-метода. Итерация №0. 1. Проверка критерия оптимальности. Текущий опорный план неоптимален, так как в индексной строке находятся отрицательные коэффициенты. 2. Определение новой базисной переменной. В качестве ведущего выберем столбец, соответствующий переменной x3, так как это наибольший коэффициент по модулю. 3. Определение новой свободной переменной. Вычислим значения Di по строкам как частное от деления: bi / ai3 и из них выберем наименьшее: min (200 : 3 , 80 : 2 , 140 : 2 ) = 40 Следовательно, 2-ая строка является ведущей. Разрешающий элемент равен (2) и находится на пересечении ведущего столбца и ведущей строки.
4. Пересчет симплекс-таблицы. Формируем следующую часть симплексной таблицы. Вместо переменной x5 в план 1 войдет переменная x3. Строка, соответствующая переменной x3 в плане 1, получена в результате деления всех элементов строки x5 плана 0 на разрешающий элемент РЭ=2. На месте разрешающего элемента получаем 1. В остальных клетках столбца x3 записываем нули. Таким образом, в новом плане 1 заполнены строка x3 и столбец x3. Все остальные элементы нового плана 1, включая элементы индексной строки, определяются по правилу прямоугольника. Для этого выбираем из старого плана четыре числа, которые расположены в вершинах прямоугольника и всегда включают разрешающий элемент РЭ. НЭ = СЭ - (А*В)/РЭ СТЭ - элемент старого плана, РЭ - разрешающий элемент (2), А и В - элементы старого плана, образующие прямоугольник с элементами СТЭ и РЭ. Представим расчет каждого элемента в виде таблицы:
Получаем новую симплекс-таблицу:
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
