ЭММ. Вариант 5. Задача 1 Графический метод решения задач линейногопрограммирования. Составить математическую модель по условию задачи

• Название: Задача 1 Графический метод решения задач линейногопрограммирования. Составить математическую модель по условию задачи
• Дата: 01.02.2021
• Размер: 171.28 Kb.
• Имя файла: ЭММ. Вариант 5.docx
• Тип: Задача; #172996
• страница: 5 из 5

2 400	3 100	4	500
A2	7 50	8	6 650	5	700
A3	6 450	9	7	2 350	800
Потребность	500	400	750	350

Целевая функция F= 8750

.


Задача 4
Теория игр
Найти оптимальные стратегии и цену игры, заданной платежной матрицей

графическим методом.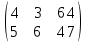



Решение:

Проверяем, имеет ли платежная матрица седловую точку. Если да, то выписываем решение игры в чистых стратегиях.

Считаем, что игрок I выбирает свою стратегию так, чтобы получить максимальный свой выигрыш, а игрок II выбирает свою стратегию так, чтобы минимизировать выигрыш игрока I.

Игроки	B1	B2	B3	B4	a = min(Ai)
A1	4	3	6	4	3
A2	5	6	4	7	4
b = max(Bi)	5	6	6	7

Находим гарантированный выигрыш, определяемый нижней ценой игры a = max(a_i) = 4, которая указывает на максимальную чистую стратегию A₂.

Верхняя цена игры b = min(b_j) = 5.

Что свидетельствует об отсутствии седловой точки, так как a ≠ b, тогда цена игры находится в пределах 4 ≤ y ≤ 5. Находим решение игры в смешанных стратегиях. Объясняется это тем, что игроки не могут объявить противнику свои чистые стратегии: им следует скрывать свои действия. Игру можно решить, если позволить игрокам выбирать свои стратегии случайным образом (смешивать чистые стратегии).

2. Проверяем платежную матрицу на доминирующие строки и доминирующие столбцы.

Иногда на основании простого рассмотрения матрицы игры можно сказать, что некоторые чистые стратегии могут войти в оптимальную смешанную стратегию лишь с нулевой вероятностью.

Говорят, что i-я стратегия 1-го игрока доминирует его k-ю стратегию, если a_ij ≥ a_kj для всех j Э N и хотя бы для одного j a_ij >a_kj. В этом случае говорят также, что i-я стратегия (или строка) – доминирующая, k-я – доминируемая.

Говорят, что j-я стратегия 2-го игрока доминирует его l-ю стратегию, если для всех j Э M a_ij ≤ a_il и хотя бы для одного i a_ij il. В этом случае j-ю стратегию (столбец) называют доминирующей, l-ю – доминируемой.

С позиции проигрышей игрока В стратегия B₁ доминирует над стратегией B₄ (все элементы столбца 1 меньше элементов столбца 4), следовательно, исключаем 4-й столбец матрицы. Вероятность q₄ = 0.

4	3	6
5	6	4

В платежной матрице отсутствуют доминирующие строки.

Мы свели игру 2 x 4 к игре 2 x 3.

Так как игроки выбирают свои чистые стратегии случайным образом, то выигрыш игрока I будет случайной величиной. В этом случае игрок I должен выбрать свои смешанные стратегии так, чтобы получить максимальный средний выигрыш.

Аналогично, игрок II должен выбрать свои смешанные стратегии так, чтобы минимизировать математическое ожидание игрока I.

3. Находим решение игры в смешанных стратегиях.

Решим задачу геометрическим методом, который включает в себя следующие этапы:

1. В декартовой системе координат по оси абсцисс откладывается отрезок, длина которого равна 1. Левый конец отрезка (точка х = 0) соответствует стратегии A₁, правый - стратегии A₂ (x = 1). Промежуточные точки х соответствуют вероятностям некоторых смешанных стратегий S₁ = (p₁,p₂).

2. На левой оси ординат откладываются выигрыши стратегии A₁. На линии, параллельной оси ординат, из точки 1 откладываются выигрыши стратегии A₂.

Решение игры (2 x n) проводим с позиции игрока A, придерживающегося максиминной стратегии. Доминирующихся и дублирующих стратегий ни у одного из игроков нет.

Выделяем нижнюю границу выигрыша B₁NB₃. Максиминной оптимальной стратегии игрока A соответствует точка N, лежащая на пересечении прямых B₁B₁ и B₃B₃, для которых можно записать следующую систему уравнений:

y = 4 + (5 - 4)p₂

y = 6 + (4 - 6)p₂

Откуда

p₁ = ¹/₃

p₂ = ²/₃

Цена игры, y = ¹⁴/₃

Теперь можно найти минимаксную стратегию игрока B, записав соответствующую систему уравнений, исключив стратегию B₂, которая дает явно больший проигрыш игроку B, и, следовательно, q₂ = 0.

4q₁+6q₃ = y

5q₁+4q₃ = y

q₁+q₃ = 1

или

4q₁+6q₃ = ¹⁴/₃

5q₁+4q₃ = ¹⁴/₃

q₁+q₃ = 1

Решая эту систему, находим:

q₁ = ²/₃.

q₃ = ¹/₃.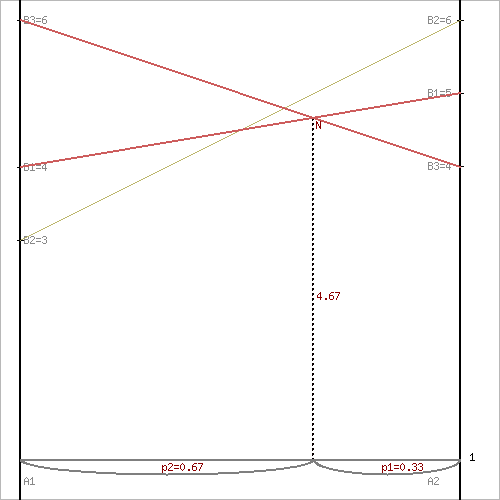



Ответ:

Цена игры: y = ¹⁴/₃, векторы стратегии игроков:

Q(²/₃, 0, ¹/₃), P(¹/₃, ²/₃)

4. Проверим правильность решения игры с помощью критерия оптимальности стратегии.

∑a_ijq_j ≤ v

∑a_ijp_i ≥ v

M(P₁;Q) = (4*²/₃) + (3*0) + (6*¹/₃) = 4.667 = v

M(P₂;Q) = (5*²/₃) + (6*0) + (4*¹/₃) = 4.667 = v

M(P;Q₁) = (4*¹/₃) + (5*²/₃) = 4.667 = v

M(P;Q₂) = (3*¹/₃) + (6*²/₃) = 5 ≥ v

M(P;Q₃) = (6*¹/₃) + (4*²/₃) = 4.667 = v

Все неравенства выполняются как равенства или строгие неравенства, следовательно, решение игры найдено верно.

Поскольку из исходной матрицы были удалены и столбцы, то найденные векторы вероятности можно записать в виде:

P(¹/₃,²/₃)

Q(²/₃,0,¹/₃,0):

Задача 5
Сетевые графики
Пусть необходимо выполнить комплекс взаимосвязанных работ. Используя данные вариантов задания, постройте сетевой график, найдите критический путь, посчитайте критическое время выполнения комплекса работ и другие временные характеристики сетевого графика. Исходные данные представлены по вариантам. Постройте график с временными характеристиками. Сделайте выводы.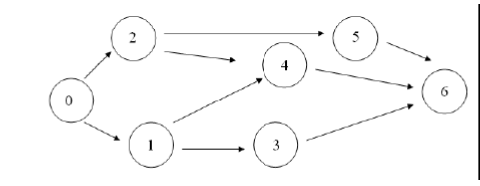

Дуги	(0;1)	(0;2)	(1;3)	(1;4)	(2;4)	(2;5)	(3;6)	(4;6)	(5;6)
tij	7	8	5	4	7	8	9	10	9

Решение:

Резерв времени события показывает, на какой допустимый период времени можно задержать наступление этого события, не вызывая при этом увеличения срока выполнения комплекса работ.

Для определения резервов времени по событиям сети рассчитывают наиболее ранние t^p и наиболее поздние t^п сроки свершения событий. Любое событие не может наступить прежде, чем свершаться все предшествующие ему события и не будут выполнены все предшествующие работы. Поэтому ранний (или ожидаемый) срок tp(i) свершения i-ого события определяется продолжительностью максимального пути, предшествующего этому событию:

t^p(i) = max(t(L_ni))

где L_ni – любой путь, предшествующий i-ому событию, то есть путь от исходного до i-ого события сети.

Если событие j имеет несколько предшествующих путей, а следовательно, несколько предшествующих событий i, то ранний срок свершения события j удобно находить по формуле:

t^p(j) = max[t^p(i) + t(i,j)]

Задержка свершения события i по отношению к своему раннему сроку не отразится на сроке свершения завершающего события (а значит, и на сроке выполнения комплекса работ) до тех пор, пока сумма срока свершения этого события и продолжительности (длины) максимального из следующих за ним путей не превысит длины критического пути. Поэтому поздний (или предельный) срок t^п(i) свершения i-ого события равен:

t^п(i) = t_kp - max(t(L_ci))

где L_ci - любой путь, следующий за i-ым событием, т.е. путь от i-ого до завершающего события сети.

Если событие i имеет несколько последующих путей, а следовательно, несколько последующих событий j, то поздний срок свершения события i удобно находить по формуле:

t^п(i) = min[t^п(j) - t(i,j)]

Резерв времени R(i) i-ого события определяется как разность между поздним и ранним сроками его свершения:

R(i) = t^п(i) - t^p(i)

Резерв времени события показывает, на какой допустимый период времени можно задержать наступление этого события, не вызывая при этом увеличения срока выполнения комплекса работ.

Критические события резервов времени не имеют, так как любая задержка в свершении события, лежащего на критическом пути, вызовет такую же задержку в свершении завершающего события. Таким образом, определив ранний срок наступления завершающего события сети, мы тем самым определяем длину критического пути.

При определении ранних сроков свершения событий tp(i) двигаемся по сетевому графику слева направо и используем формулы (1), (2).

Расчет сроков свершения событий.

Для i=0 (начального события), очевидно tp(0)=0.

i=1: t^p(1) = t^p(0) + t(0,1) = 0 + 7 = 7.

i=2: t^p(2) = t^p(0) + t(0,2) = 0 + 8 = 8.

i=3: t^p(3) = t^p(1) + t(1,3) = 7 + 5 = 12.

i=4: max(t^p(1) + t(1,4);t^p(2) + t(2,4)) = max(7 + 4;8 + 7) = 15.

i=5: t^p(5) = t^p(2) + t(2,5) = 8 + 8 = 16.

i=6: max(t^p(3) + t(3,6);t^p(4) + t(4,6);t^p(5) + t(5,6)) = max(12 + 9;15 + 10;16 + 9) = 25.

Длина критического пути равна раннему сроку свершения завершающего события 6: t_kp=tp(6)=25

При определении поздних сроков свершения событий t_п(i) двигаемся по сети в обратном направлении, то есть справа налево и используем формулы (3), (4).

Для i=6 (завершающего события) поздний срок свершения события должен равняться его раннему сроку (иначе изменится длина критического пути): t^п(6)= t^р(6)=25

Далее просматриваются строки, оканчивающиеся на номер предпоследнего события, т.е. 5. Просматриваются все строчки, начинающиеся с номера 5.

i=5: t^п(5) = t^п(6) - t(5,6) = 25 - 9 = 16.

Далее просматриваются строки, оканчивающиеся на номер предпоследнего события, т.е. 4. Просматриваются все строчки, начинающиеся с номера 4.

i=4: t^п(4) = t^п(6) - t(4,6) = 25 - 10 = 15.

Далее просматриваются строки, оканчивающиеся на номер предпоследнего события, т.е. 3. Просматриваются все строчки, начинающиеся с номера 3.

i=3: t^п(3) = t^п(6) - t(3,6) = 25 - 9 = 16.

Далее просматриваются строки, оканчивающиеся на номер предпоследнего события, т.е. 2. Просматриваются все строчки, начинающиеся с номера 2.

i=2: min(t^п(4) - t(2,4);t^п(5) - t(2,5)) = min(15 - 7;16 - 8) = 8.

Далее просматриваются строки, оканчивающиеся на номер предпоследнего события, т.е. 1. Просматриваются все строчки, начинающиеся с номера 1.

i=1: min(t^п(3) - t(1,3);t^п(4) - t(1,4)) = min(16 - 5;15 - 4) = 11.

Далее просматриваются строки, оканчивающиеся на номер предпоследнего события, т.е. 0. Просматриваются все строчки, начинающиеся с номера 0.

i=0: min(t^п(1) - t(0,1);t^п(2) - t(0,2)) = min(11 - 7;8 - 8) = 0.

Таблица 1 - Расчет резерва событий

Номер события	Сроки свершения события: ранний tp(i)	Сроки свершения события: поздний tп(i)	Резерв времени, R(i)
0		0	0
1	7	11	4
2	8	8	0
3	12	16	4
4	15	15	0
5	16	16	0
6	25	25	0

В данном случае имеются несколько критических путей:

Критический путь №1:(0,2)(2,4)(4,6)

Критический путь №2:(0,2)(2,5)(5,6)

Продолжительность критического пути: 25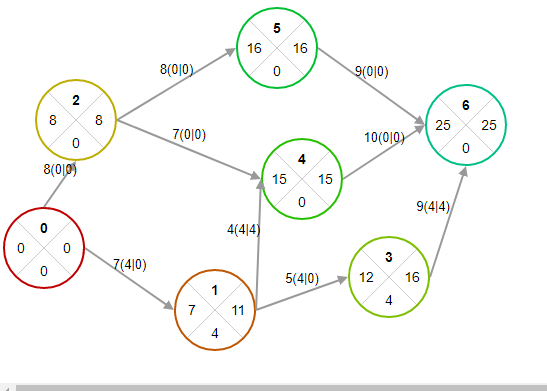



Рис. 1 - Сетевой график с нанесенными временными характеристиками.
Список использованной литературы

1. 
   Вентцель, Е. С. Исследование операций. Задачи, принципы, методо­логия / Е. С. Вентцель. - М. : Наука, 2016. – 345 с.
   
2. 
   Курицкий, Б. Я. Поиск оптимальных решений средствами EXCEL 7.0 / Б. Я.Курицкий. -СПб. : BHV-Санкт-Петербург, 2016. – 389 с.
   
3. 
   Математическое моделирование экономических процессов на желез­нодорожном транспорте / под ред. А. Б. Каплана. - М. : Транспорт, 2017. – 390 с.
   
4. 
   Математическое программирование / под ред. Н. Ш. Кремера. - М. : Финстатинформ, 2018. – 389 с.
   
5. 
   Мур, Дж. Экономическое моделирование в MicrosoftExcel / Дж. Мур, Л. Р. Уэдерфорд. – М: АСТ, 2019. – 239 с.