контр. статистика Вариант 26. Задача 1 (N17) По результатам летней сессии 2010 г знания студентов по статистике всех форм обучения были оценены следующим образом

• Название: Задача 1 (N17) По результатам летней сессии 2010 г знания студентов по статистике всех форм обучения были оценены следующим образом
• Дата: 05.11.2022
• Размер: 464.5 Kb.
• Имя файла: контр. статистика Вариант 26.doc
• Тип: Задача; #771668
• страница: 2 из 2

Из таблицы 2.3 видно, что с ростом жилой площади квартир (Х₂) увеличивается и цена квартиры (Y), а площадь кухни (Х₃) меняется неоднозначно. Но в целом также прослеживается рост площади кухни с ростом жилой площади квартиры.

2. По исходным данным рассчитаем общую дисперсию цены квартиры Y.
Таблица 2.4 – Расчёт дисперсии цены квартиры

№ п/п (i)	Yi
1	22	484
2	24,7	610,09
3	15,9	252,81
4	15,4	237,16
5	15,6	243,36
6	24,4	595,36
7	21,3	453,69
8	21,5	462,25
9	19	361
10	24,2	585,64
11	21,2	449,44
12	25	625
13	18,2	331,24
14	20,1	404,01
15	17,8	316,84
16	19,8	392,04
17	22,4	501,76
18	17,8	316,84
19	21,1	445,21
20	28	784
21	34,4	1183,36
22	30,8	948,64
23	34,1	1162,81
24	37,7	1421,29
25	36,7	1346,89
∑	589,1	14914,73
Среднее	23,564	596,5892

Дисперсия (общая):

По таблице 2.3 находим межгрупповую дисперсию: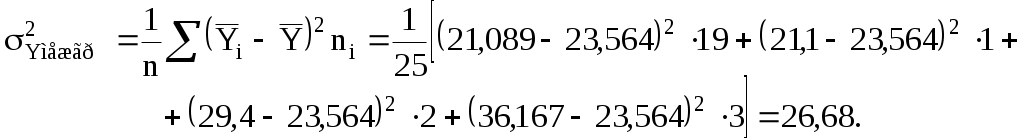



Составим таблицу для определения внутригрупповых дисперсий.
Таблица 2.5 – Определение внутригрупповых дисперсий

Группа	Y	Y2
№ 1	22	484
	24,7	610,09
	15,9	252,81
	15,4	237,16
	15,6	243,36
	24,4	595,36
	21,3	453,69
	21,5	462,25
	19	361
	24,2	585,64
	21,2	449,44
	25	625
	18,2	331,24
	20,1	404,01
	17,8	316,84
	19,8	392,04
	22,4	501,76
	17,8	316,84
	34,4	1183,36
∑	400,7	8805,89
Среднее	21,089	463,468
№ 2	21,1	445,21
∑	21,1	445,21
Среднее	21,1	445,21
№ 3	28	784
	30,8	948,64
∑	58,8	1732,64
Среднее	29,4	866,32
№ 4	34,1	1162,81
	37,7	1421,29
	36,7	1346,89
∑	108,5	3930,99
Среднее	36,167	1310,330

Внутригрупповые дисперсии:



Средняя из внутригрупповых дисперсий:



Проверка:

Коэффициент детерминации: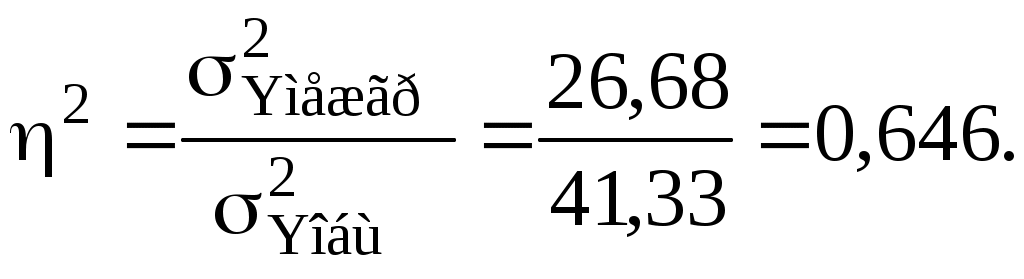



Эмпирическое корреляционное отношение:



По коэффициенту детерминации можно сделать вывод, что 64,6% вариации цены квартиры обусловлены вариацией жилой площади квартиры.

3. Произведём далее группировку квартир по двум факторам – Х₂ (жилая площадь) и Х₃ (площадь кухни). Для этого используем результаты группировки из таблицы 2.2. Всю совокупность квартир по площади кухни разбиваем (кроме разбивки по Х₂) ещё на 3 группы по фактору Х₃ величиной .

Результаты группировки сводим в таблицу 2.6.
Таблица 2.6 – Группировка квартир по жилой площади и площади кухни

Группа строящихся квартир по Х2, м2	Подгруппа квартир по Х3, м2	Y, тыс.у.е.	Х2, м2	Х3, м2
16,0-22,35	7,4-10,6	24,7	20,6	10,4
		15,9	17,8	8,3
		15,4	17,8	8,3
		15,6	20,0	8,3
		21,3	18,0	8,1
		21,5	20,0	9,2
		19,0	19,0	7,4
		24,2	21,0	10,2
		21,2	19,2	10,1
		25,0	20,0	10,2
		18,2	20,0	10,2
		20,1	20,0	10,2
		17,8	17,5	8,3
		17,8	19,3	8,4
	∑	277,7	270,2	127,6
	Среднее	19,84	19,30	9,11
	10,6-13,8	22,0	17,7	11,0
		24,4	22,3	12,4
		19,8	16,0	11,0
		22,4	21,2	11,2
		34,4	21,4	11,0
	∑	123	98,6	56,6
	Среднее	24,6	19,72	11,32
Итого	-	400,7	368,8	184,2
В среднем	-	21,089	19,411	9,695
22,35-28,7	10,6-13,8	21,1	28,0	10,7
	∑	21,1	28,0	10,7
	Среднее	21,1	28,0	10,7
Итого	-	21,1	28,0	10,7
В среднем	-	21,1	28,0	10,7
28,7-35,05	7,4-10,6	28,0	31,1	10,0
		30,8	29,7	9,4
	∑	58,8	60,8	19,4
	Среднее	29,4	30,4	9,7
Итого	-	58,8	60,8	19,4
В среднем	-	29,4	30,4	9,7
35,05-41,4	10,6-13,8	34,1	35,4	13,0
		37,7	41,4	12,1
	∑	71,8	76,8	25,1
	Среднее	35,9	38,4	12,55
	13,8-17,0	36,7	35,5	17,0
	∑	36,7	35,5	17,0
	Среднее	36,7	35,5	17,0
Итого	-	108,5	112,3	42,1
В среднем	-	36,167	37,433	14,033
Всего	-	589,1	569,9	256,4
В среднем	-	23,564	22,796	10,256

Итоги группировки таблицы 2.6 сводим в таблицу 2.7.
Таблица 2.7 – Итоги группировки квартир по жилой площади и площади кухни

Группа строящихся квартир по Х2, м2	Подгруппа квартир по Х3, м2	Средняя цена квартиры, тыс.у.е.	Средняя жилая площадь, м2	Средняя площадь кухни, м2
16,0-22,35	7,4-10,6	19,84	19,30	9,11
	10,6-13,8	24,6	19,72	11,32
	13,8-17,0	-	-	-
В среднем по группе	-	21,089	19,411	9,695
22,35-28,7	7,4-10,6	-	-	-
	10,6-13,8	21,1	28,0	10,7
	13,8-17,0	-	-	-
В среднем по группе	-	21,1	28,0	10,7
28,7-35,05	7,4-10,6	29,4	30,4	9,7
	10,6-13,8	-	-	-
	13,8-17,0	-	-	-
В среднем по группе	-	29,4	30,4	9,7
35,05-41,4	7,4-10,6	-	-	-
	10,6-13,8	35,9	38,4	12,55
	13,8-17,0	36,7	35,5	17,0
В среднем по группе	-	36,167	37,433	14,033
В среднем по совокупности	-	23,564	22,796	10,256

Из таблицы 2.7 не прослеживается однозначной динамики между жилой площадью и площадью кухни.
Задача № 3 (вариант 7)



Решение

1. Рассматриваем исходные данные по варианту 7 из задания 2 по цене квартир.

Y
21,3
21,5
19,0
24,2
21,2
25,0
18,2
20,1
17,8
19,8
22,4
17,8
21,1
28,0
34,4
30,8
34,1
37,7
36,7
26,4
34,2
35,6
46,6
35,7
30,8

По данной совокупности построим интервальный вариационный ряд из 4-х интервалов длины . Результаты сводим в таблицу 1.

Таблица 1 – Интервальный ряд цены квартир

Интервал (yi-yi+1)	17,8-25,0	25,0-32,2	32,2-39,4	39,4-46,6
Середина интервала, zi	21,4	28,6	35,8	43,0
Число квартир, fi	12,5	4,5	7	1
fi/n, n=25	0,5	0,18	0,28	0,04
fi/(nh)	0,0694	0,0250	0,0389	0,0056

Здесь варианта 25,0 попала на границу двух интервалов - первого и второго. Поэтому она с частотой ½ отнесена и в первый, и во второй интервалы.

2. Строим гистограмму распределения.
n_i/(nh)

0 ,0700






0,0350






0 17,8 25,0 32,2 39,4 46,6 x
3. Мода (варианта, имеющая наибольшую частоту):





Здесь x_Mo – начало модального интервала (интервала с наибольшей частотой), f_Mo – частота модального интервала, f_Mo-1 – частота предмодального интервала, f_Mo+1 – частота послемодального интервала, h_Mo – величина модального интервала. В данном случае модальным является первый интервал, так как у него наибольшая частота.

Медиана (варианта, расположенная в середине ряда распределения):



Здесь x_Me – начало медианного интервала, h_Me – величина медианного интервала, f_Me – частота медианного интервала, S_Me-1 – накопленная сумма частот до медианного интервала. Так как то в качестве медианного интервала можно взять как первый, так и второй интервал. Выше при расчётах в качестве медианного взят первый интервал.

4. Для определения числовых характеристик выборки составим расчётную таблицу.

Таблица 2 – Расчёт числовых характеристик

zi	fi	zifi
21,4	12,5	267,5	5724,5	77,4
28,6	4,5	128,7	3680,8	4,536
35,8	7	250,6	8971,5	57,456
43,0	1	43	1849	15,408
∑	25	689,8	20226	154,8
Среднее	-	27,592	809,03	6,192

Размах вариации:

Средняя цена квартиры:

Среднее линейное отклонение цены:

Дисперсия цены:

Среднеквадратическое отклонение:

Коэффициент вариации:

Задача № 4 (вариант 29)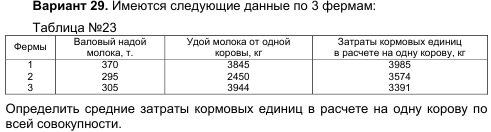



Решение

Пусть ВН – валовой надой молока, У – удой молока от одной коровы, УКЕ – затраты кормовых единиц в расчёте на одну корову. Количество коров K_i по i-й ферме можно найти по формуле: K_i = ВН_i / У_i. Затраты кормовых единиц по i-й ферме: 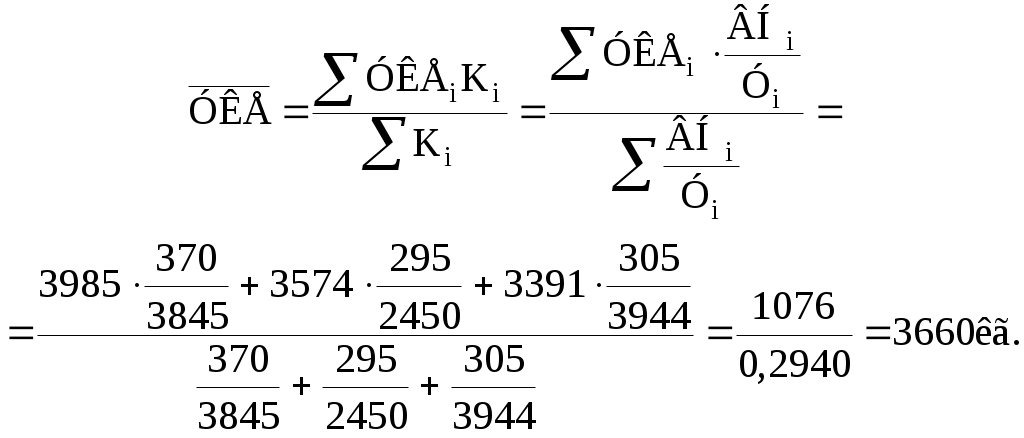Средние затраты кормовых единиц на одну корову по всей совокупности по формуле средней арифметической взвешенной:



Таким образом, по всем фермам затраты кормовых единиц в среднем на одну корову составляют 3660 кг.

Список использованных источников

1. 
   Даукш И. А. Статистика: Учеб.-практ. пособие / И. А. Даукш, Н. Э. Титенкова. – Минск: БГЭУ, 2004. – 111 с.
   
2. 
   Колесникова И. И. Статистика: учеб. пособие / И. И. Колесникова, Г. В. Круглякова. – Москва: Новое знание, 2006. - 208 с.
   
3. 
   Микроэкономическая статистика: Учебник / Под ред. С. Д. Ильенковой. – Москва: Финансы и статистика, 2004. – 544 с.
   
4. 
   Общая теория статистики: Учеб.-практ. пособие. / Л. А. Сошникова, В. А. Тарловская, И. Н. Терлиженко и др.; Под ред. И. Н. Терлиженко. – Минск.: БГЭУ, 2004. – 134 с.