Задача 1. Пусть а в. Упростить выражения а в, АВ, а в с, АВС
 Скачать 0.77 Mb. Скачать 0.77 Mb.
|
                                                                                                                         Задача №1. Задача №1.1.1. Пусть А 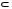 В. Упростить выражения А В. Упростить выражения А  В, А+В, А В, А+В, А  В В  С, А+В+С. С, А+В+С.1.2. Бросаются две игральные кости. Пусть А- событие, состоящее в том, что сумма очков нечетная, В - событие, состоящее в том, что хотя бы на одной из костей выпала единица. Описать события 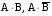 . .1.3. Дана система S, состоящая из блоков 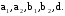 Записать событие S, состоящее в том, что система S исправна. Записать событие S, состоящее в том, что система S исправна.a1 a2 b1 b2 d 1.4. Пусть А,В,С - три произвольных события. Найти выражения, если: - произошло только событие А; - произошло одно и только одно событие; - произошло два и только два события; - все три события произошли; - произошло не более двух событий. 1.5. Пусть событие А - падает снег, событие В - идет дождь. Выразить через А и Вследующие события: а) дождь со снегом; б) дождь или снег; в) нет дождя; г) ясная погода; д) падает снег без дождя. 1.6. Бросаются две игральные кости: одна черная, а другая белая. Отмечается число очков, выпавших на каждой кости. Сколько элементарных событий соответствует тому, что а) сумма очков больше 10? б) сумма очков - четная? 1.7. Машинно-котельная установка состоит из двух котлов и одной машины. Событие А - исправна машина, событие Вк( к = 1,2) - исправен k-й котел. Событие Созначает работоспособность машинно-котельной установки, что будет в том случае, если исправна машина и хотя бы один котел. Выразить события С и 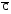 через А и Вк . через А и Вк .1.8. Образуют ли полную группу следующие наборы событий (дать полный ответ, доказать). Опыт: а) Бросание двух монет; события: А 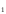 - появление двух гербов, А - появление двух гербов, А - появление двух цифр. - появление двух цифр.б) Два выстрела по мишени; события: 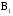 - хотя бы попадание, В - хотя бы попадание, В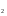 - хотя бы один промах. - хотя бы один промах.1.9. Образуют ли полную группу следующие группы событий (дать полный ответ, доказать). Опыт: а) Бросание игральной кости; события: А1- появление не менее трех очков, А2- появление не более четырех очков. б) Два выстрела по мишени; cобытия: В1 - ни одного попадания, В2 - одно попадание,В3 - два попадания? 1.10. Производится наблюдение за группой, состоящей из четырех однородных объектов. Каждый из них за время наблюдения может быть обнаружен или не обнаружен. Рассматриваются события: А - обнаружен ровно один из четырех объектов, В - обнаружен хотя бы один объект. Указать (с доказательством), в чем состоят события А + В; А  В. В.1.11. Каковы соотношения между событиями А,В и С, если АВС=А; если А+В+С=А? Дать геометрическую интерпретацию. 1.12. Назвать противоположные события для следующих событий: С - три по-падания при трех выстрелах; Д - хотя бы одно попадание при пяти выстрелах. 1.13. Назвать противоположные события для следующих событий: А - не более двух попаданий при пяти выстрелах, В - выигрыш первого игрока при игре в шахматы. 1.14. Событие В есть частный случай события А, т.е. из появления события В следует, что событие А произошло. Следует ли из 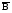 , что , что 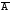 произошло? Следует ли из произошло? Следует ли из 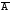 событие событие 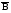 ? ?1.15. Мишень состоит из десяти кругов, ограниченных концентрическими окружностями с радиусами 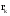 (к=1,2,...,10), причем r2< r2< ...< r10. Событие Аk – попадание в круг радиусом rk. Что означают события (к=1,2,...,10), причем r2< r2< ...< r10. Событие Аk – попадание в круг радиусом rk. Что означают события 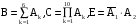 . Что представляет собой событие . Что представляет собой событие 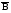 ? ?1.16. События А - хотя бы один из трех проверяемых приборов бракованный, В - все приборы доброкачественные. Что означают события А+В, А·В. 1.17. Пусть А и В - случайные события. Доказать, что А, 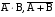 образуют полную группу. образуют полную группу.1.18. По мишени стреляют одиночными выстрелами до первого попадания, после чего стрельбу прекращают. Записать событие, которое должно иметь место для того, чтобы был произведен четвертый выстрел? Будет ли это событие противоположно тому событию, что произведено не более трех выстрелов? 1.19. Имеется электрическая схема 3 1 2 6 4 5 Выразить через события Аi ( i-й контакт замкнут) и  ( i-й контакт разомкнут) следующие события: С- лампочка горит и ( i-й контакт разомкнут) следующие события: С- лампочка горит и 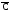 - лампочка не горит. - лампочка не горит.1.20. Прибор состоит из трех блоков первого типа и четырех блоков второго типа. Событие Аi ( i = 1, 2, 3)– исправен i-й блок первого типа, Вj ( j = 1, 2, 3, 4)- исправен j-й блок второго типа. Прибор работает, если исправен хотя бы один блок первого типа и не менее трех блоков второго типа. Найти выражение для события С, которое соответствует работе прибора. 1.21. Пусть Ai- событие, состоящее в том, что при i-м повторении эксперимента осуществилось событие А; 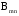 - событие, состоящее в том, что при nпервых повторениях эксперимента событие А осуществилось m раз. Выразить - событие, состоящее в том, что при nпервых повторениях эксперимента событие А осуществилось m раз. Выразить 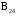 через через 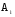 . .1.22. Два шахматиста играют одну партию. Событие А - выиграет первый игрок, В- выиграет второй игрок. Какое событие следует добавить к указанной совокупности, чтобы получилась полная группа событий? 1.23. Опыт - передача двух сигналов. Относительно перечисленных событий указать, образуют ли они в данном опыте полную группу событий: А - хотя бы один сигнал искажен, B- хотя бы один сигнал не искажен. 1.24. Опыт - эксплуатируются два прибора в течение времени  t. Рассматривая события: А - ни один прибор не вышел из строя, В - один прибор вышел из строя, а другой нет, С - оба прибора вышли из строя. Ответить на следующие вопросы: образуют ли они полную группу, являются ли несовместными, являются ли равновозможными. t. Рассматривая события: А - ни один прибор не вышел из строя, В - один прибор вышел из строя, а другой нет, С - оба прибора вышли из строя. Ответить на следующие вопросы: образуют ли они полную группу, являются ли несовместными, являются ли равновозможными.1.25. Равны ли события А и В, если а) 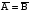 ; б) А+С = В+С; в) АС=ВС; ; б) А+С = В+С; в) АС=ВС;1.26. Среди студентов, собравшихся на лекцию, выбирают наудачу одного. Пусть событие А заключается в том, что выбранный окажется юношей. Событие В - в том, что он играет на гитаре, а событие С - в том, что он живет в общежитии. Описать событие АВС. При каком условии будет иметь место тождество АВС=А? Когда будет равенство А=В? Будет ли оно иметь место, если все юноши играют на гитаре? 1.27. Производится наблюдение за группой, состоящей из четырех однородных объектов. Каждый из них за время наблюдения может быть обнаружен или не обнаружен. Рассматриваются события: В - обнаружен хотя бы один объект; С -обнаружено не менее двух объектов, D - обнаружено ровно два объекта; Е -обнаружено ровно три объекта, F - обнаружены все четыре объекта. Указать, в чем состоят события D+Е+F, ВС. 1.28. Событие А - хотя бы одно из имеющихся четырех изделий бракованное, событие В - бракованных изделий среди них не менее двух. Что означают противоположные события 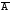 и и  ? ?1.29. Опыт - передача (в одинаковых условиях) трех сообщений равной длины. Рассматривая события: А - искажено первое сообщение; В - искажено второе сообщение; С - искажено третье сообщение. Ответить на следующие вопросы: образуют ли они полную группу, являются ли несовместными, являются ли равновозможными? 1.30. Опыт – Брошены 2 игральные кости. Образуют ли полную группу событий следующие наборы: А - на обеих костях шестерки, В - ни на одной кости нет шестерки, С - на одной из костей шестерка, на другой – нет. (Указать, образуют ли они в данном опыте полную группу событий). Задача №2. 2.1. В конверте среди 100 фотокарточек находится разыскиваемая карточка. Из конверта наудачу извлекают 10 карточек. Найти вероятность того, что среди них окажется нужная карточка. 2.2. Из пяти букв разрезной азбуки составлено слово "книга". Ребенок, не умеющий читать, рассыпал эти буквы и затем собрал в произвольном порядке. Найти вероятность того, что у него получилось слово "книга". 2.3. В партии готовых изделий, содержащей 20 штук, имеется 4 бракованных. Партию делят на две равные части. Какова вероятность, что бракованные изделия разделятся поровну? 2.4. В урне 2 белых и 4 черных шара. Из урны один за другим вынимаются все шары, находящиеся в урне. Найти вероятность того, что последний вынутый шар будет черным. 2.5. В группе студентов 17 юношей и 8 девушек. Какова вероятность того, что студент, фамилия которого в списке группы находится на первом месте, окажется девушкой? 2.6. Какова вероятность того, что номер билета студента четный? Делится на пять? Оканчивается нулем? (Предполагается, что студенческих билетов достаточно большое число). 2.7. В партии готовой продукции, состоящей из 20 изделий, три бракованных. Определить вероятность того, что при случайном выборе 4 изделий одновременно все они окажутся небракованными. Какова вероятность того, что бракованных и небракованных изделий окажется поровну? 2.8. В партии готовой продукции из 20 лампочек имеется 5 лампочек повышенного качества. В выборку отбирается 7 лампочек. Какова вероятность того, что в этой выборке окажется 3 лампочки повышенного качества? 2.9. В первом ящике находятся шары с номерами 1, 2, 3, 4,5. Во втором ящике -шары с номерами 6, 7, 8, 9,10. Из каждого ящика вынули по одному шару. Какова вероятность того, что сумма номеров вынутых шаров не меньше 7? Какова вероятность того, что сумма номеров равна 11 ? 2.10. Какова вероятность того, что взятый наудачу год содержит 53 воскресенья, если это год невисокосный; високосный? 2.11. Найти вероятность того, что среди пяти случайно взятых цифр нет совпадающих. 2.12. На пяти карточках написаны буквы а, д, к, л, о. После тщательного перемешивания берут по одной карточке и кладут последовательно рядом. Какова вероятность того, что получится слово "лодка"? 2.13. Группа, которую составляют 10 мужчин и 10 женщин, делится на две равные части. Найти вероятность того, что в каждой части будет по одинаковому числу мужчин и женщин. 2.14. Буквы а, а, в, к, к, о, x написаны на отдельных карточках. Какова вероятность того, что извлекая эти карточки по одной наудачу (без возвращения обратно), получим в порядке их выхода слова "Каховка"? 2.15. Телефонный номер состоит из пяти цифр. Найти вероятность того, что все цифры различны. 2.16. Найти вероятность того, что при шести бросаниях игральной кости появятся все грани. 2.17. В магазине работает 10 продавцов, из них 6 женщин. В смену заняты 3 продавца. Найти вероятность того, что в наудачу укомплектованную смену войдут все 3 продавца мужчины. 2.18. На 8 одинаковых карточках написаны соответственно числа 2, 4, 6, 7, 8, 11, 12 и 13. Наугад берутся 2 карточки. Определить вероятность того, что из двух полученных чисел дробь сократима. 2.19.Четырехтомное сочинение стоит на полке в случайном порядке. Какова вероятность того, что номера томов образуют монотонную последовательность? 2.20. Из 15 билетов выигрышными являются4. Какова вероятность того, что среди взятых наудачу 6 билетов будет 2 выигрышных? 2.21. В урне находятся 16 шаров, помеченных номерами 1, 2, 3, ..., 16. Наудачу извлечены 5 шаров (без возвращения). Найти вероятность того, что среди извлеченных шаров окажутся шары с номерами 1 и2. 2.22. Из последовательности целых чисел1...10 наудачу выбираются 2 числа. Какова вероятность того, что одно из них меньше 6, а другое больше 6? 2.23. Группа из n человек , в том числе А и В, располагается за круглым столом в случайном порядке. Найти вероятность того, что между А и В будет сидеть ровно r человек 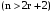 . .2.24. Из тридцати карточек с буквами русского алфавита наугад выбираются 4 карточки. Какова вероятность, что эти четыре карточки в порядке выхода составят слово "небо"? 2.25. Вычислить вероятность того, что дни рождения всех r (r £ 365)человек различны, предполагая, что в году 365 дней и что все дни рождения одинаково вероятны для каждого человека. 2.26. Трое пассажиров входят в лифт пятиэтажного дома. Какова вероятность того, что двое из них выйдут на одном этаже? Вероятность выхода пассажиров на каждом этаже считается одинаковой. 2.27. Группа из 10 человек садится на скамейку. Какова вероятность того, что два определенных лица окажутся рядом? 2.28. В ящике содержится 100 деталей, из них 10 бракованных. Наудачу извлечены 4 детали. Найти вероятность того, что среди извлеченных деталей нет бракованных; нет годных? 2.29. На отдельных карточках выписаны цифры 1, 2, 3, 4, 5, 6, 7, 8,9. Все девять карточек тщательно перемешаны, после чего наугад берут одну из них, записывают цифру и возвращают карточку назад. Какова вероятность того, что после выписывания четырех цифр получится четное число? число 1234? 2.30. На складе имеется 15 кинескопов, причем 10 из них изготовлены Львовским заводом. Найти вероятность того, что среди наудачу взятых 5 кинескопов окажется 3 кинескопа Львовского завода. 2.31. Слово "Машина" составлено из букв разрезной азбуки. Определить вероятность того, что при произвольном извлечении без возвращения 4 букв в порядке их выхода образуется слово "шина". 2.32. В розыгрыше первенства по баскетболу участвуют 18 команд, среди которых имеется 5 команд экстракласса. Случайным образом формируются 2 группы по 9 команд в каждой. Найти вероятность того, что все команды экстракласса попадут в одну и ту же группу. 2.33. На 9 карточках написаны цифры 0, 1, 2, 3, 4, 5, 6, 7,8. Две из них вынимаются наугад и укладываются на стол в порядке появления, затем читается полученное число, например, 07,14 и т.п. Найти вероятность того, что число будет четное. 2.34. Четыре человека входят в лифт пятиэтажного дома. Какова вероятность, что все они выйдут на разных этажах, если выход пассажира на любом этаже равновозможен ? 2.35. Телефонный номер состоит из 5 цифр. Найти вероятность того, что цифры одинаковы. 2.36. Из шести букв разрезной азбуки составлено слово "ананас". Ребенок, неумеющий читать, рассыпал эти буквы и затем собрал в произвольном порядке. Найти вероятность того, что у него снова получилось слово "ананас". 2.37. Из колоды в 32 карты берутся наугад 10 карт. Найти вероятность того, что среди них будут 8 карт одной масти. 2.38. В лифт семиэтажного дома на первом этаже вошли два человека. Каждый из них с одинаковой вероятностью выходит на любом из этажей, начиная со второго. Найти вероятность того, что оба пассажира выйдут на пятом этаже. 2.39. Колода карт (52 карты) произвольным образом делится пополам. Найти вероятность того, что в каждой половине будет по два туза. 2.40. Брошены две игральные кости. Найти вероятность того, что сумма очков на выпавших гранях равна пяти, а произведение четырем. 2.41. Среди 25 деталей, подвергаемых проверке, имеются 15 точных. Какова вероятность того, что из числа взятых наудачу 10 деталей окажется 8 точных? 2.42. Лифт в пятиэтажном доме отправляется с тремя пассажирами. Найти вероятность того, что на каждом этаже выйдет не более одного пассажира, предполагая, что все возможные способы распределения пассажиров по этажам равновероятны. 2.43. Для уменьшения общего количества игр на соревнованиях 16 волейбольных команд разбиты на 2 подгруппы (по 8 в каждой). Найти вероятность того, что две наиболее сильные команды окажутся в разных подгруппах, в одной подгруппе? 2.44. Бросаются одновременно две игральные кости. Найти вероятность того, что сумма выпавших очков кратна5. 2.45. В шахматном турнире участвуют 20 человек, которые будут распределены по жребию для игры в двух группах по 10 человек. Какова вероятность, что двое наиболее сильных участников турнира будут играть в разных группах? 2.46. В группе из 30 учеников на контрольной работе 6 учеников получили оценку отлично, 10 - оценку хорошо, 9 учеников - оценку удовлетворительно, 5 учеников - оценку неудовлетворительно. Какова вероятность того, что три ученика, вызванные к доске, имеют неудовлетворительную оценку по контрольной работе? 2.47. Куб, все грани которого окрашены, распилен на 125 кубиков одинакового размера. Все кубики перемешаны. Определить вероятность того, что кубик, извлеченный наудачу, будет иметь три окрашенные грани. 2.48. Слово «керамит» составлено из букв разрезной азбуки. Затем карточки с буквами перемешиваются, из них извлекаются по очереди четыре карточки. Какова вероятность, что эти четыре карточки в порядке выхода составят слово «река»? 2.49. В автобусе 5 пассажиров. Найти вероятность того, что на каждой из оставшихся 5 остановок будет сходить по одному пассажиру. Предполагается, что каждый из пассажиров с равной вероятностью может выйти на любой из остановок. 2.50. Каждая из букв слова "интеграл" написана на одной из восьми карточек. Карточки перемешиваются. Найти вероятность того, что при извлечении трех карточек появится (в порядке их выхода) слово "три". 2.51. Найти вероятность угадывания в "Спортлото" 4-х цифр (всего 49 цифр). 2.52. В квадрат наудачу бросается точка. Найти вероятность того, что она попадет внутрь круга, вписанного в квадрат. 2.53. На 10 из 20 карточек написана цифра “1”, а на остальных 10 - цифра “0”. Пять карточек вынимают наугад. Найти вероятность того, что на двух карточках будет стоять цифра “1”, а на трех - цифра “0” (безразлично в каком порядке). 2.54. В урне «a» белых и «b» черных шаров. Из урны вынимают один шар и откладывают в сторону. Этот шар оказался белым. После этого из урны берут еще один шар. Найти вероятность того, что этот шар тоже будет белым. 2.55. В урне «a» белых и «b» черных шаров (a ³ 2).Из урны вынимают сразу два шара. Найти вероятность того, что оба шара будут белыми. 2.56. Из ящика, содержащего n перенумерованных изделий, наугад вынимают одно за другим находящиеся в нем изделия, каждое изделие после вынимания вкладывается обратно и перемешивается с другим, а его номер записывается. Найти вероятность того, что будет записана естественная последовательность номеров: 1,2..., n. 2.57. В отделение связи поступило 4 телеграммы, всего имеется четыре канала связи. Телеграммы случайным образом распределяются по каналам, каждая телеграмма с одной и той же вероятностью передается по любому из четырех каналов. Найти вероятность того, что на один из каналов попадут три телеграммы, на другой - одна, а два оставшихся канала будут незагружены. 2.58. Бросаются две игральные кости. Определить вероятность того, что сумма очков не превышает пяти. 2.59. В отрезке единичной длины наудачу появляется точка. Определить вероятность того, что расстояние от концов отрезка превосходит величину 1/5. 2.60. Имеются изделия четырех сортов, причем число изделий первого сорта – 1, второго сорта - 2, третьего сорта - 3, четвертого сорта -4. Для контроля наудачу берут 7 изделий. Определить вероятность того, что среди них одно изделие первосортное, одно - второго сорта, два - третьего и три - четвертого сорта. |
