Задача 1. Пусть а в. Упростить выражения а в, АВ, а в с, АВС
 Скачать 0.77 Mb. Скачать 0.77 Mb.
|
Х 1 3 5 7 9Р 0,1 0,2 0,3 0,3 0,1Найти распределение случайной величины  6.24. В шестиламповом радиоприемнике (все лампы различные) перегорела одна лампа. С целью устранения неисправности наудачу выбранную лампу заменяют заведомо годной из запасного комплекта, после чего сразу проверяется работа приемника. Составить закон распределения числа замен ламп. 6.25. Имеется 5 ключей, из которых только один подходит к замку. Составить закон распределения числа попыток при открывании замка, если испробованный ключ в последующих попытках: а) не участвует; б) участвует. 6.26. В лотерее разыгрывается мотоцикл стоимостью 250 р., велосипед стоимостью 50 р. и часы за 40 р. Найти математическое ожидание выигрыша для лица, имеющего: а) 1 билет; б) 2 билета, если общее число билетов равно 100. 6.27. Из ящика, содержащего 2 белых и 4 черных шара, вынимают 3 шара и перекладывают в другой ящик, где имелось 5 белых шаров. Найти математическое ожидание числа белых шаров Х1 и Х2 в обоих ящиках. 6.28. В урне 4 белых и 5 черных шаров. Из урны наудачу один за другим без возвращения извлекают шары до тех пор, пока не появится черный шар. Найти закон распределения, математическое ожидание и дисперсию числа появившихся при извлечении белых шаров. Построить функцию распределения. Определить вероятность того, что число белых шаров будет не менее трех. 6.29. В партии из 7 деталей имеется 5 деталей первого сорта. Наудачу отобраны 3 детали. Найти закон распределения, математическое ожидание и дисперсию числа деталей первого сорта среди отобранных. Определить вероятность того, что число деталей первого сорта будет не менее двух. 6.30. Вероятность попадания в цель из орудия при первом выстреле равна 0,1, при втором выстреле равна 0,4, при третьем - 0,7. Предполагается произвести три выстрела. Найти закон распределения, математическое ожидание и дисперсию числа попаданий в цель. Построить функцию распределения. Определить вероятность того, что число попаданий не менее трех. Задача №7. 7.1. Дана функция распределения случайной величины X: 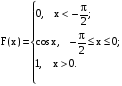 Найти вероятность попадания случайной величины X в интервал 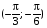 и показать эту вероятность на графиках плотности и функции распределения. Найти математическое ожидание и дисперсию. и показать эту вероятность на графиках плотности и функции распределения. Найти математическое ожидание и дисперсию.7.2. График плотности распределения непрерывной случайной величины X имеет вид f(x) Найти функции f(x) и F(х). Вычислить М[Х]. x -2 0 4 7.3. График плотности распределения непрерывной случайной величины Xимеет вид f(x) Найти математическое ожидание, дисперсию и среднее квадрати- ческое отклонение. 0 2 x 7.4.Случайная величина X задана плотностью распределения 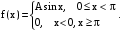 Найти коэффициент A . Определить математическое ожидание и дисперсию случайной величины X. Найти функцию распределения и вероятность того, что значения случайной величины будут находиться в интервале (0; Найти коэффициент A . Определить математическое ожидание и дисперсию случайной величины X. Найти функцию распределения и вероятность того, что значения случайной величины будут находиться в интервале (0; 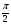 ). ).7.5. Дана плотность распределения непрерывной случайной величины X: 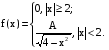 Найти коэффициент A . Определить математическое ожидание и среднее квадратическое отклонение. 7.6. Случайная величина X распределена по "Закону прямоугольного треугольника" в интервале (0, а). f(x) x 0 а Написать выражение плотности распределения. Найти функцию распределения. Найти вероятность попадания случайной величины X на участок от а/2 до а. Найти характеристики случайной величины Х: 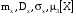 . .7.7. Известна функция распределения срока службы блока 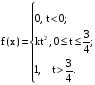 Найти коэффициент K .Найти средний срок службы и дисперсию срока службы блока. 7.8. Плотность вероятности случайной величины Х задана функцией:  Найти ее функцию распределения, построить графики плотности вероятности и функции распределения. 7.9. Плотность распределения времени безотказной работы электронно-лучевой трубки имеет вид (по закону Вейбулла)   Найти функцию распределения случайной величины T и вероятность безотказной работы трубки в течение 4 часов. 7.10. Случайная величина X подчинена закону Симпсона ("Закону равнобедренного треугольника") на участке от -a до a . f(x) x -a 0 a Написать выражение плотности распределения. Найти функцию распределения. Найти числовые характеристики случайной величины X: 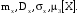 Найти вероятность попадания случайной величины X в интервал (-a/2; a ). Найти вероятность попадания случайной величины X в интервал (-a/2; a ). 7.11. Плотность распределения непрерывной случайной величины в интервале 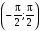 равна равна 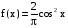 , вне этого интервала f(x) =0. Найти вероятность того, что в трех независимых испытаниях случайная величина X примет ровно два раза значение, заключенное в интервале (0; , вне этого интервала f(x) =0. Найти вероятность того, что в трех независимых испытаниях случайная величина X примет ровно два раза значение, заключенное в интервале (0; ) . ) .7.12. Дана плотность распределения вероятностей непрерывной случайной величины  Найти функцию распределения. Построить графики функций f(x) и F(X) . 7.13. Найти математическое ожидание и дисперсию случайной величины X, распределенной в интервале (  ) с плотностью вероятностей ) с плотностью вероятностей 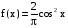 , вне этого интервала f(x) = 0. , вне этого интервала f(x) = 0.7.14. Дана плотность вероятности случайной величины X: 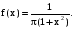 Построить графики функций f(x) и F(x). Найти вероятность попадания случайной величины X в интервал ( -1; 1) и показать ее на графиках. Построить графики функций f(x) и F(x). Найти вероятность попадания случайной величины X в интервал ( -1; 1) и показать ее на графиках.7.15. Непрерывная случайная величина X задана законом распределения 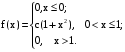 Найти: 1) коэффициент C; 2) функцию распределения F(x); 3) математическое ожидание и дисперсию X. 7.16. Случайная величина X задана плотностью распределения:  Найти:1) коэффициент C; 2) функцию распределения F(x); 3) вероятность попадания случайной величины на интервал (/6; /4); 4) математическое ожидание X. 7.17. Непрерывная случайная величина подчинена закону распределения с плотностью  Найти коэффициент c, М[X], D[X]. Построить график функции распределения F(x). 7.18. Плотность распределения случайной величины Х задана графически : f(х) Написать выражение плотности распре- деления f(х); найти функцию распре- деления и построить ее график; найти математическое ожидание и дисперсию. 0 2 4 x 7.19. Случайная величина X распределена логарифмически нормально, т. е. ее плотность 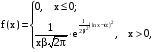 где а - любое действительное число, 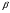 - положительно. Найти M[X]. - положительно. Найти M[X].7.20. Плотность распределения вероятности случайной величины 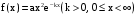 . Требуется: а) найти коэффициент a ,б) найти функцию распределения случайной величины X , в) вычислить вероятность попадания случайной величины в интервал (0; 1/k). . Требуется: а) найти коэффициент a ,б) найти функцию распределения случайной величины X , в) вычислить вероятность попадания случайной величины в интервал (0; 1/k).7.21. Плотность распределения вероятности случайных амплитуд боковой качки корабля имеет вид (закон Рэлея)  .Определить: а) функцию распределения случайной величины X; б) математическое ожидание M[X], дисперсию D[X] , среднее квадратическое отклонение x. .Определить: а) функцию распределения случайной величины X; б) математическое ожидание M[X], дисперсию D[X] , среднее квадратическое отклонение x.7.22. Функция f(x) равна нулю при - < x < 1 и равна  , если 1 , если 1  x < +. Найти: а) значение A , при котором эта функция будет плотностью вероятности некоторой случайной величины X; б) функцию распределения этой случайной величины; в) вероятность того, что в четырех независимых испытаниях она ни разу не попадает в интервал (1; 2). x < +. Найти: а) значение A , при котором эта функция будет плотностью вероятности некоторой случайной величины X; б) функцию распределения этой случайной величины; в) вероятность того, что в четырех независимых испытаниях она ни разу не попадает в интервал (1; 2).7.23. Функция  является плотность распределения вероятности случайной величины Х. Определить: а) коэффициент А; б) функцию распределения F(x), в) вероятность того, что случайная величина Х примет значение, не меньше единицы. является плотность распределения вероятности случайной величины Х. Определить: а) коэффициент А; б) функцию распределения F(x), в) вероятность того, что случайная величина Х примет значение, не меньше единицы.7.24. Случайная величина X может принимать только неотрицательные значения, ее функция распределения  . Найти: а) плотность распределения вероятности; б) математическое ожидание M[X]. Построить графики f(x) и F(x). . Найти: а) плотность распределения вероятности; б) математическое ожидание M[X]. Построить графики f(x) и F(x).7.25. Случайная величина X имеет плотность распределения вероятности  Определить коэффициент "a" и построить график плотности. Найти функцию распределения F(x). 7.26. Случайная величина X подчинена закону  распределения с плотностью распределения с плотностью  Найти коэффициент a. Построить график плотности. Найти вероятность попадания случайной величины X в интервал (1; 2). 7.27. Случайная величина X задана функцией распределения  Вычислить вероятность попадания случайной величины X в интервал (1; 2,5). Найти плотность распределения f(x), математическое ожидание M[X], дисперсию D[X]. 7.28. Дана функция  При каком значении функция f(x) может быть принята за плотность распределения вероятности случайной величины X? Определить это значение , найти математическое ожидание и среднее квадратическое отклонение случайной величины X . 7.29. Плотность распределения случайной величины  Найти начальные и центральные моменты первых четырех порядков, коэффициент асимметрии и эксцесс. 7.30. Функция распределения случайной величины X имеет вид: 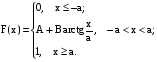 Определить: 1)при каких значениях A и B функция распределения является непрерывной; 2) плотность распределения вероятностей f(x); 3) P(-a/2 < X< a/2). Задача №8. 8.1. Случайная величина Х - число попаданий мячом в корзину при трех бросках. Вероятность попадания при каждом броске равна P. Найти матема-тическое ожидание и дисперсию этой случайной величины. 8.2. Функция распределения случайной величины Х задана графиком F(x) 1 x 0 a b Найти математическое ожидание и дисперсию случайной величины Х. 8.3. Система состоит из 4-х дублирующих блоков, надежность каждого из которых равна P. Число блоков, отказавших за фиксированное время работы системы, есть случайная величина X. Найти ее математическое ожидание и дисперсию. 8.4. Вероятность отказа определенного транзистора после оговоренного числа лет работы равна «р» , а вероятность того, что он будет работать исправно после этого времени, равна 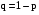 . Проведена проверка n транзисторов. Построить ряд распределения числа неисправных транзисторов в партии для значений 0, 1, 2, 3, 4, 5, 6, если n = 100, p = 0,02. Вычислить математическое ожидание. . Проведена проверка n транзисторов. Построить ряд распределения числа неисправных транзисторов в партии для значений 0, 1, 2, 3, 4, 5, 6, если n = 100, p = 0,02. Вычислить математическое ожидание.8.5. Найти математическое ожидание случайной величины, заданной функцией распределения  8.6. Случайная величина Х, возможные значения которой неотрицательны, задана функцией распределения F(x) = 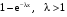 . Найти математическое ожидание этой случайной величины. . Найти математическое ожидание этой случайной величины.8.7. Случайная величина X подчинена показательному закону с параметром 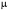 : : 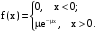 Построить кривую распределения. Найти функцию распределения. Найти вероятность того, что случайная величина X примет меньшее значение, чем ее математическое ожидание. 8.8. Подлежат исследованию 1200 проб руды. Пусть вероятность про-мышленного содержания металла в каждой пробе равна 0,9. Найти математическое ожидание и дисперсию числа проб с промышленным содержанием металла. 8.9. Функция распределения непрерывной случайной величины Х - времени безотказной работы некоторого устройства равна 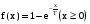 . Найти вероятность безотказной работы устройства за время . Найти вероятность безотказной работы устройства за время  8.10. Математическое ожидание числа отказов радиоаппаратуры за 10000 ч. работы равно10. Определить вероятность отказа радиоаппаратуры за 100 ч. работы. Предполагается, что отказы независимы и вероятность каждого отказа от опыта к опыту не изменяется. 8.11. Игральная кость бросается три раза. Записать закон распределения числа появлений шестерки. 8.12. Монета бросается три раза. Записать в виде таблицы закон распреде-ления случайной величины Х - числа выпадений герба. 8.13. Вероятность попадания в мишень при одном выстреле равна 0,07. Построить ряд распределения случайной величины Х - числа попаданий в мишень при двух выстрелах. Найти функцию распределения и построить ее график. 8.14. Плотность распределения вероятностей случайной величины Х имеет вид: 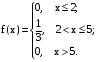 Найти функцию распределения случайной величины Х и построить ее график. Вычислить 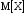 и и 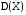 . Найти вероятность того, что случайная величина примет значение, заключенное между 2,5 и 3,5. . Найти вероятность того, что случайная величина примет значение, заключенное между 2,5 и 3,5.8.15. Случайная величина Х имеет равномерное распределение на интерва- ле (2; 3). Найти плотность распределения, математическое ожидание и дисперсию случайной величины Х. 8.16. Автомашина проходит технический осмотр и обслуживание. Число неисправностей, обнаруженных во время техосмотра, распределяется по закону Пуассона с параметром "а". Если неисправностей не обнаружено, техническое обслуживание машины продолжается в среднем 2 ч. Если обнаружены одна или две неисправности, то на устранение каждой из них тратится в среднем еще полчаса. Если обнаружено больше двух неисправностей, то машина ставится на профилактический ремонт, где она находится в среднем 4 ч. Определить закон распределения среднего времени обслуживания и ремонта машины и его математическое ожидание 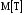 . .8.17. Случайная величина Х распределена равномерно с 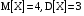 . Найти плотность распределения случайной величины Х. . Найти плотность распределения случайной величины Х.8.18. На колышек одно за другим набрасывается 4 кольца, причем вероятность попадания для каждого броска одна и та же и равна 0,8. Найти закон распределения, математическое ожидание и дисперсию числа колец, попавших на колышек, если броски независимы. 8.19. Вероятность того, что изделие не выдержит испытание, равна 0,001. Найти вероятность того, что из 5000 изделий более чем одно не выдержит испытание. 8.20. Плотность распределения случайной величины Х имеет вид: f(x) |
