|
|
Теория вероятностей. Задача 1 Пусть а в. Упростить выражения а в, АВ, а в с, АВС
 y y
 1 1
-1 1 x
-1
11.13. Система случайных величин (X, Y) подчинена закону распределения с плотностью:
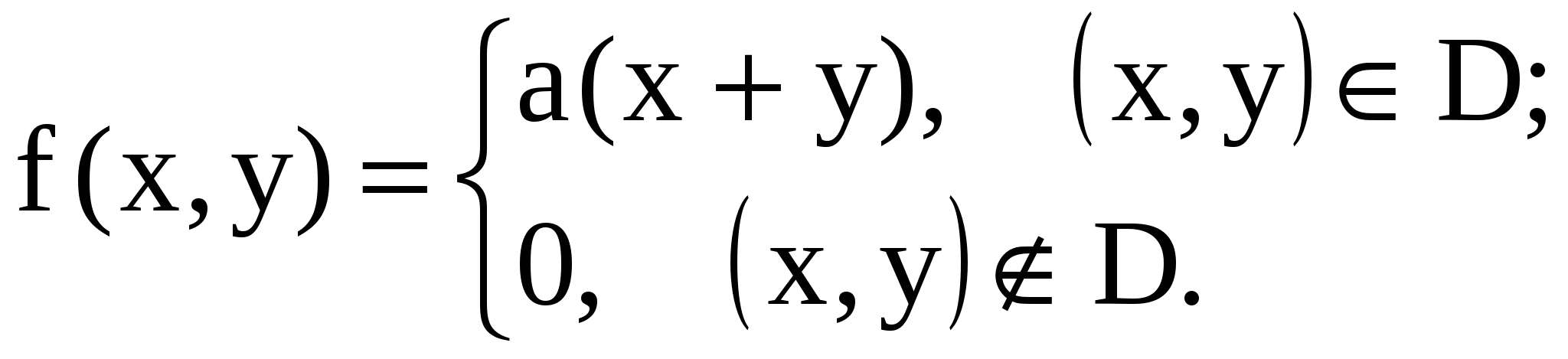
Область D - квадрат, ограниченный линиями x = 0; x = 3; y = 0; y = 3.
Найти: а) Коэффициент a; б) вероятность попадания случайной точки (x, y) в квадрат, ограниченный прямыми x = 1, x = 2, y = 1, y = 2; в) 
11.14. Определить плотность распределения вероятностей, математические ожидания и корреляционную матрицу системы случайных величин (X, Y), если 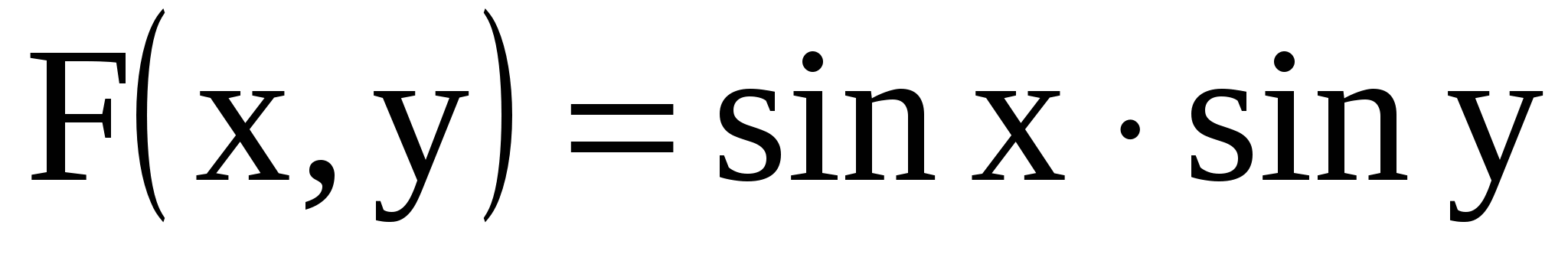 , , 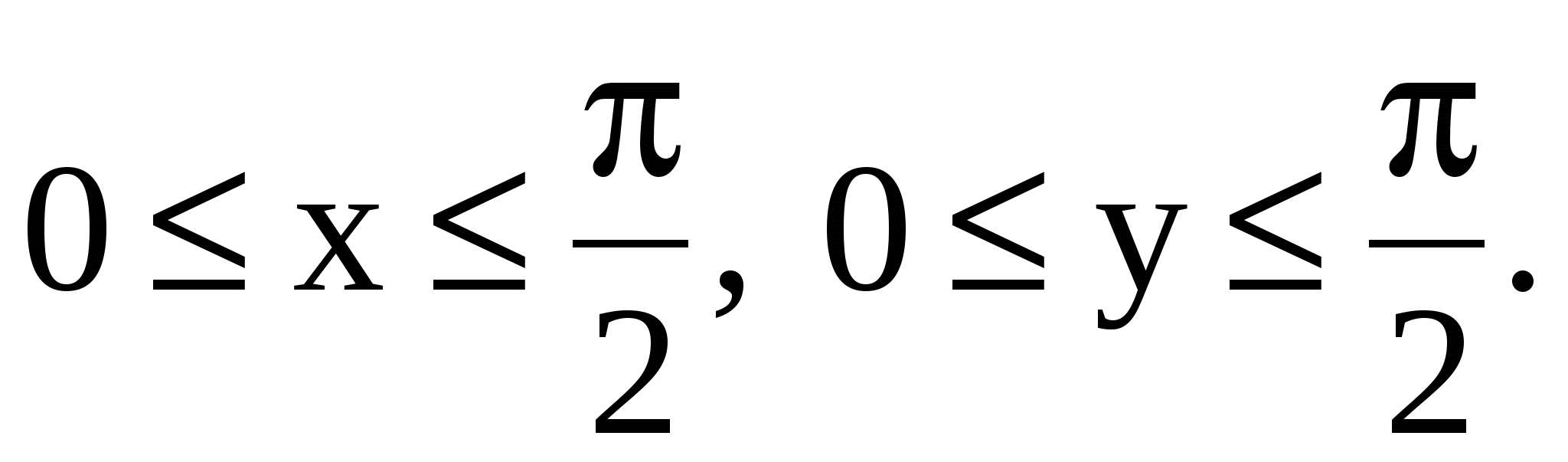
11.15. Плотность совместного распределения случайных величин (X,Y): 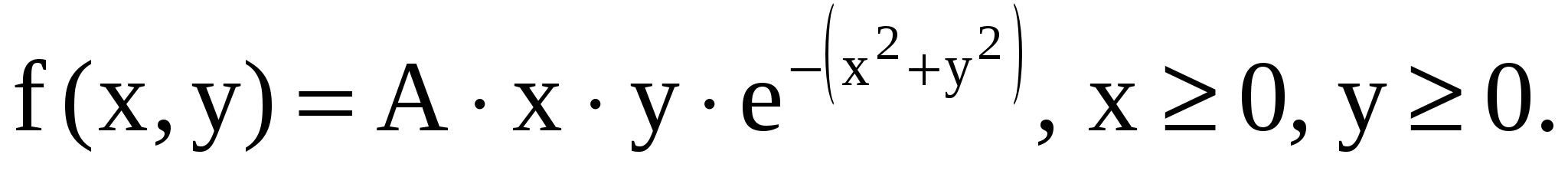 Определить: 1) коэффициент A; 2) законы распределения каждой из случайных величин, входящих в систему; 3) математичес- Определить: 1) коэффициент A; 2) законы распределения каждой из случайных величин, входящих в систему; 3) математичес-
кие ожидания каждой из случайных величин.
11.16. Плотность совместного распределения системы случайных величин X, Y равна 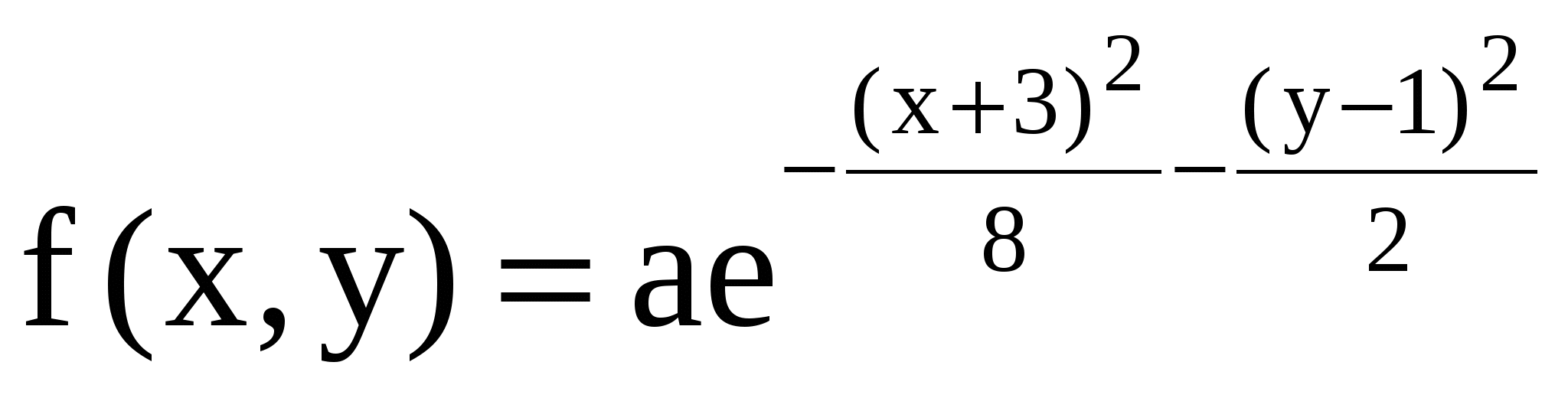 . Найти коэффициент a. Установить, являются ли величины зависимыми. Определить вероятность совместного выполнения двух неравенств x < -3; y < 4. . Найти коэффициент a. Установить, являются ли величины зависимыми. Определить вероятность совместного выполнения двух неравенств x < -3; y < 4.
11.17. Координаты случайной точки (X,Y) раcпределены равномерно внутри прямоугольника, ограниченного прямыми x = 0, x = a, y = 0, y = b. Определить вероятность попадания случайной точки в круг радиуса R = a ,если a > b, а центр круга совпадает с началом координат.
11.18. Координаты (X, Y) случайной точки распределены равномерно внутри прямоугольника, ограниченного прямыми x = a, x = b, y = c , y = d (в > a , d > c). Найти плотность распределения вероятностей и функцию распределения системы случайных величин X, Y. Выяснить, являются ли X, Y независимыми величинами.
11.19. Плотность совместного распределения случайных величин X, Y равна:
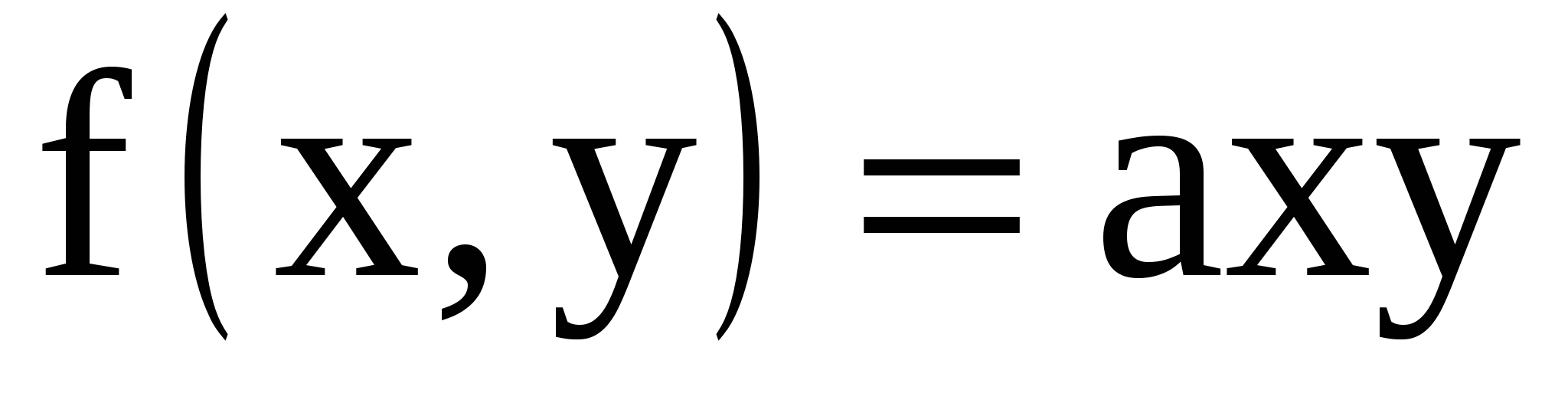 в области D и f(x,y)=0 вне этой области. Область D- треугольник, ограниченный прямыми в области D и f(x,y)=0 вне этой области. Область D- треугольник, ограниченный прямыми 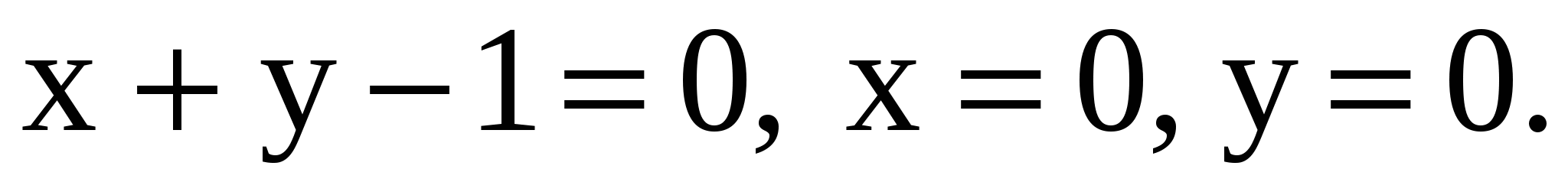 Найти а) Найти а) 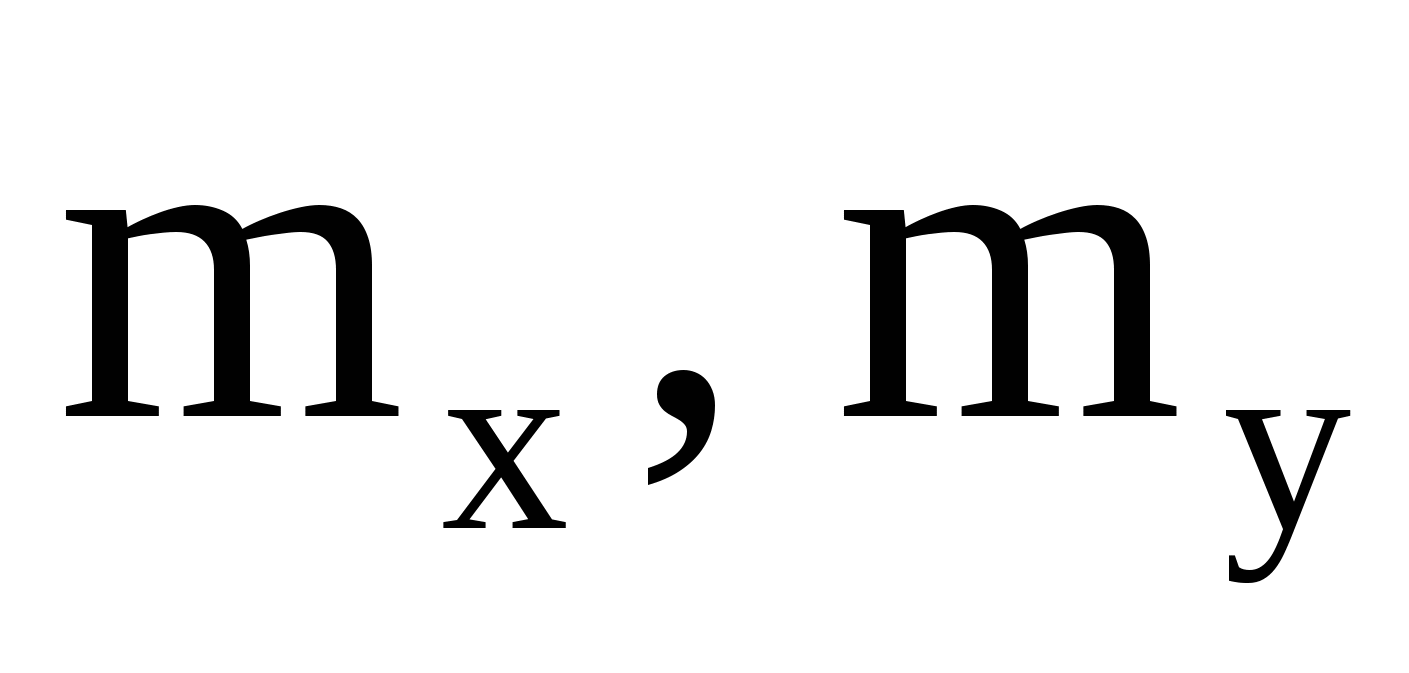 ; б) коэффициент корреляции ; б) коэффициент корреляции 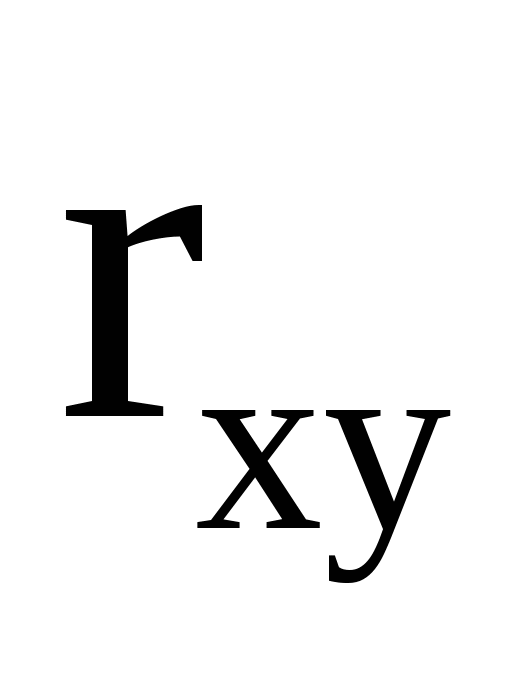 , дисперсии , дисперсии 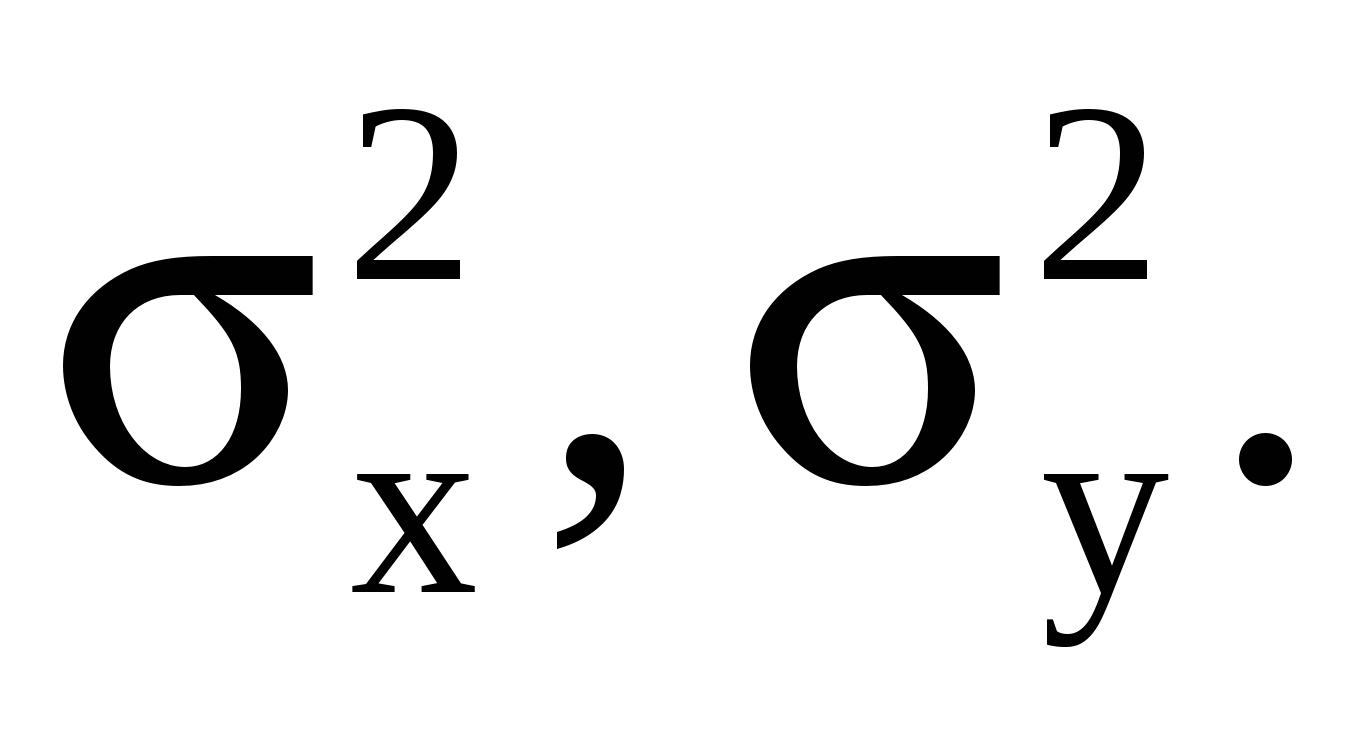
11.20. Плотность совместного распределения системы случайные величины
(X, Y), заданной внутри круга радиуса R , равна 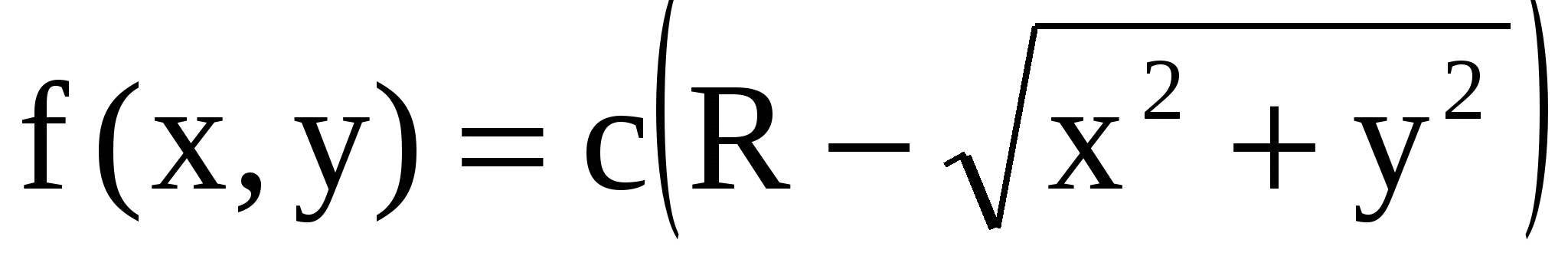 . Опреде-лить: 1) постоянную C; 2) вероятность попадания в круг радиуса a < R, если центры обоих кругов совпадают с началом координат. . Опреде-лить: 1) постоянную C; 2) вероятность попадания в круг радиуса a < R, если центры обоих кругов совпадают с началом координат.
11.21. Плотность совместного распределения системы случайных величин
(X, Y):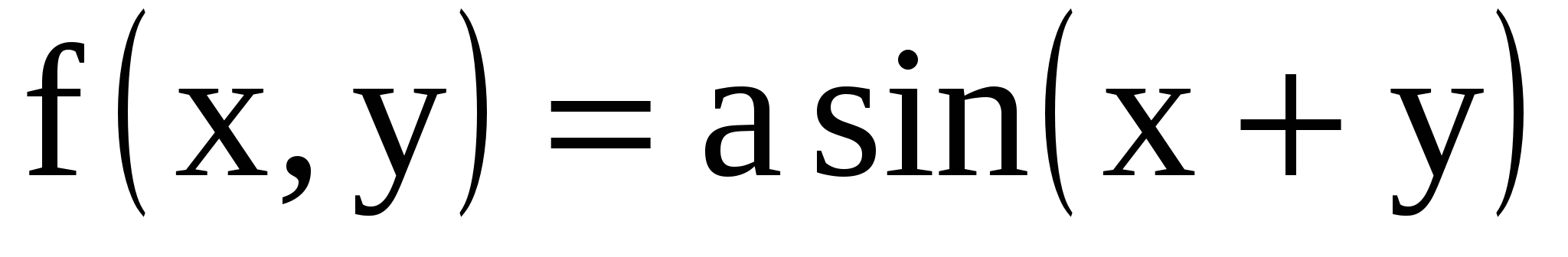 в области D и в области D и 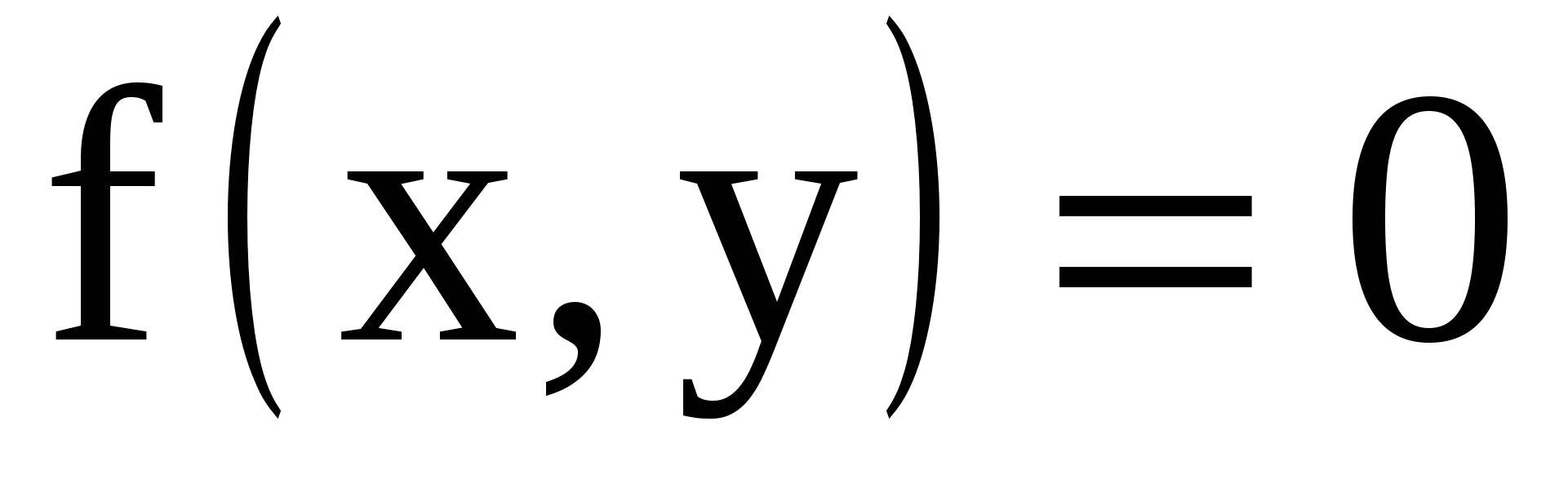 вне этой области. Область D определяется неравенствами вне этой области. Область D определяется неравенствами 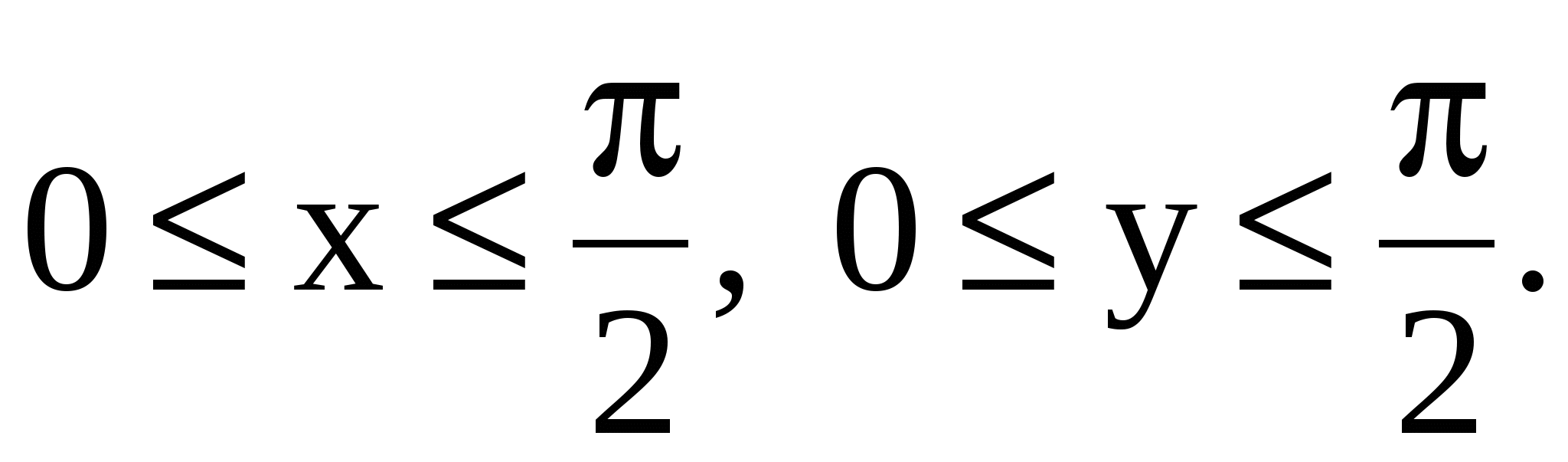 Определить: a) постоянную a; Определить: a) постоянную a;
б) 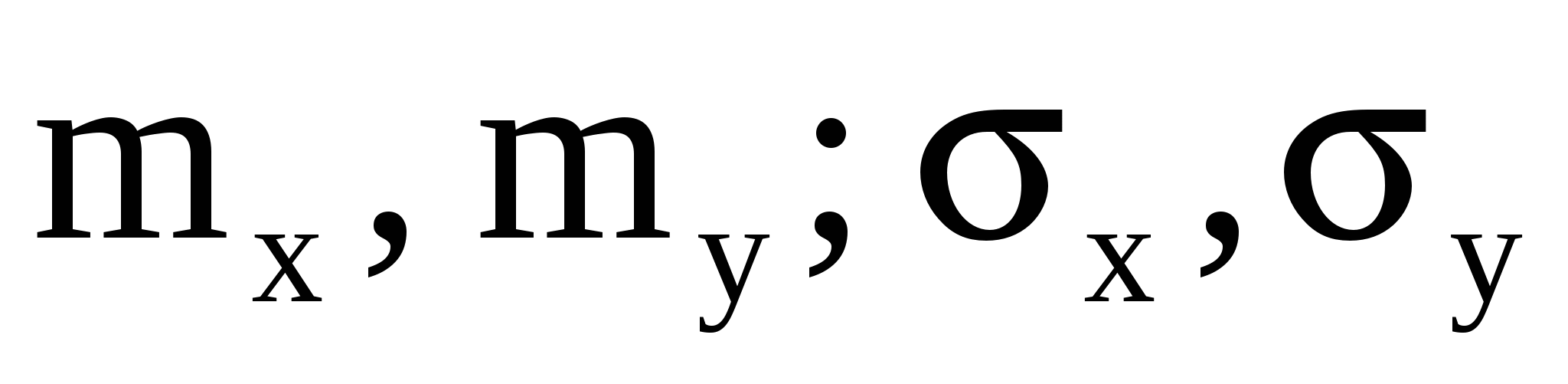 ; в) определить коэффициент корреляции r xy. ; в) определить коэффициент корреляции r xy.
11.22. Дана плотность совместного распределения системы случайных величин 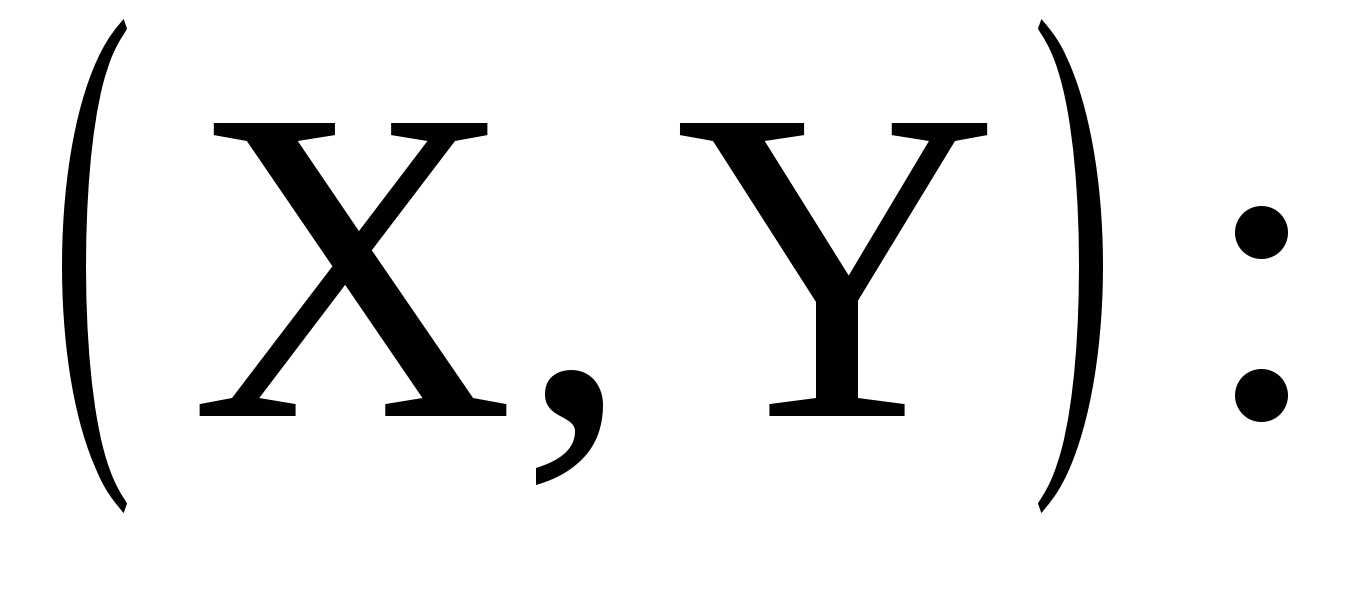 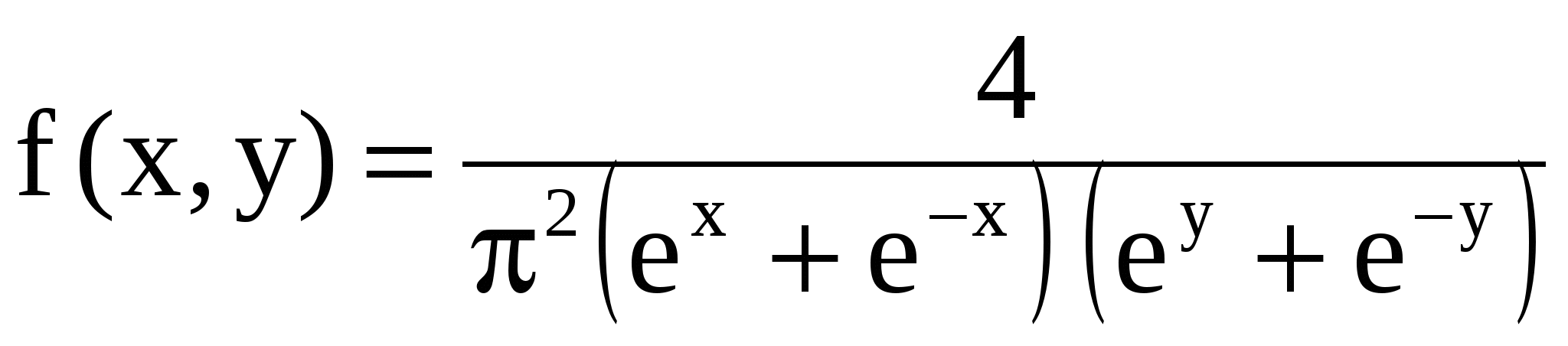 . Определить вероятность попадания случайной точки (x, y) в прямоугольник с вершинами в точках (0; 0), (1; 0), (0; 1), (1; 1). . Определить вероятность попадания случайной точки (x, y) в прямоугольник с вершинами в точках (0; 0), (1; 0), (0; 1), (1; 1).
11.23. Плотность распределения вероятностей двумерного случайного вектора (X, Y)имеет следующий вид: 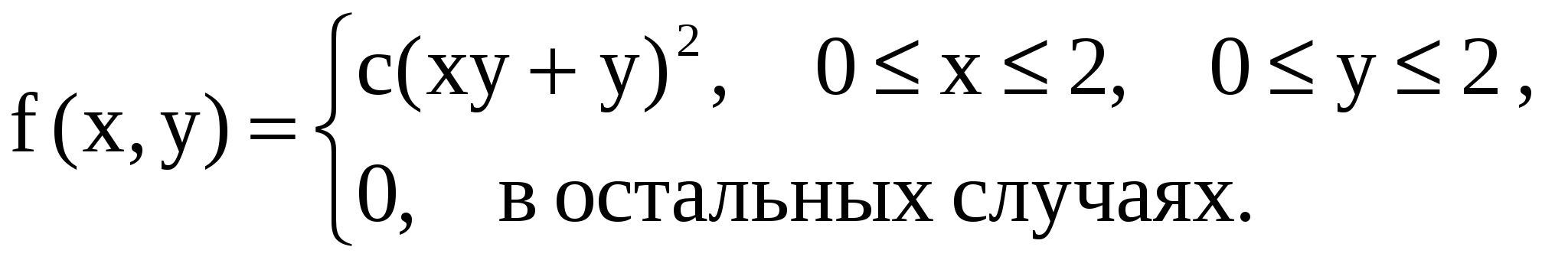 . .
Вычислить: а) значение постоянной c; б) вероятность 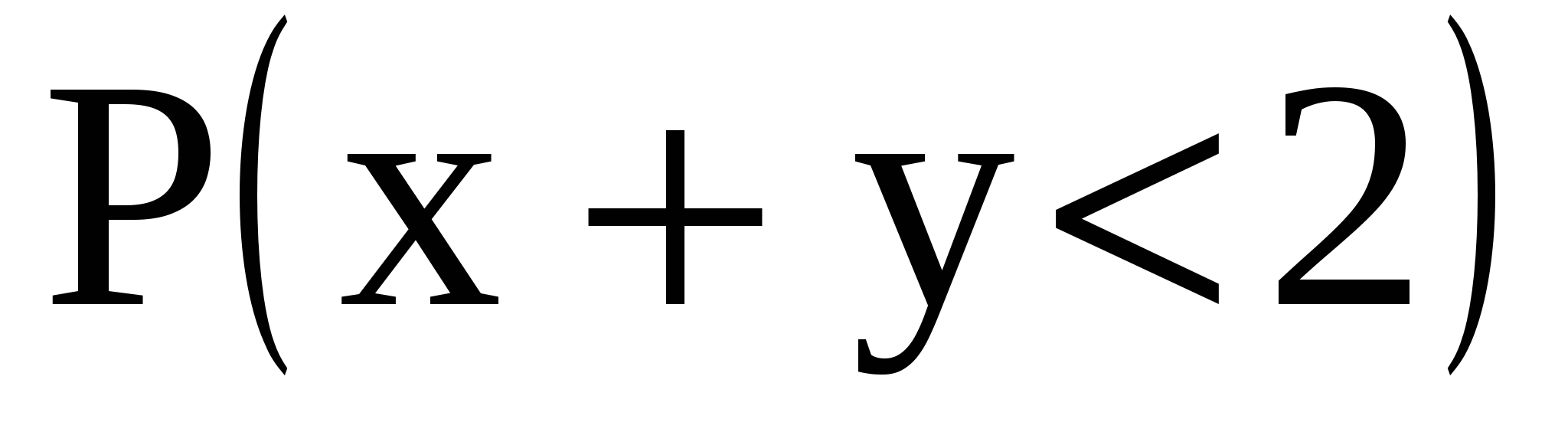 ); в) центр рассеивания. ); в) центр рассеивания.
11.24. Случайные величины X и Y независимы и распределены каждая по показательному закону с параметрами соответственно 1 и 2. Найти вероятность 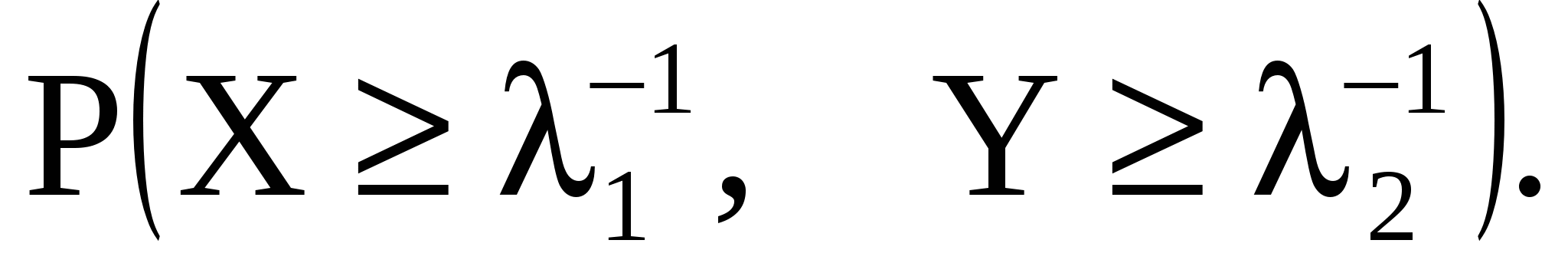
11.25. Функция совместного распределения двух случайных величин X и Y имеет следующий вид:
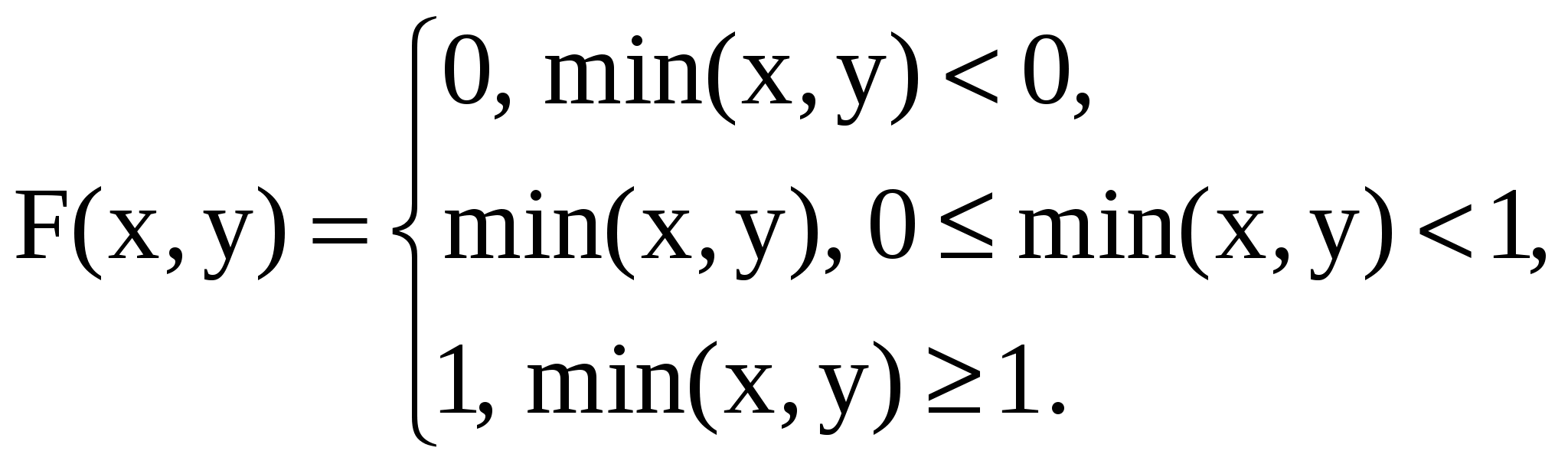
Найти одномерные законы распределения компонент и решить вопрос об их зависимости или независимости.
11.26. Случайные величины X и Y независимы и распределены следующим образом: X - по закону N(1; 2), Y - по равномерному закону на отрезке [0; 2].
Найти вероятность следующих событий: 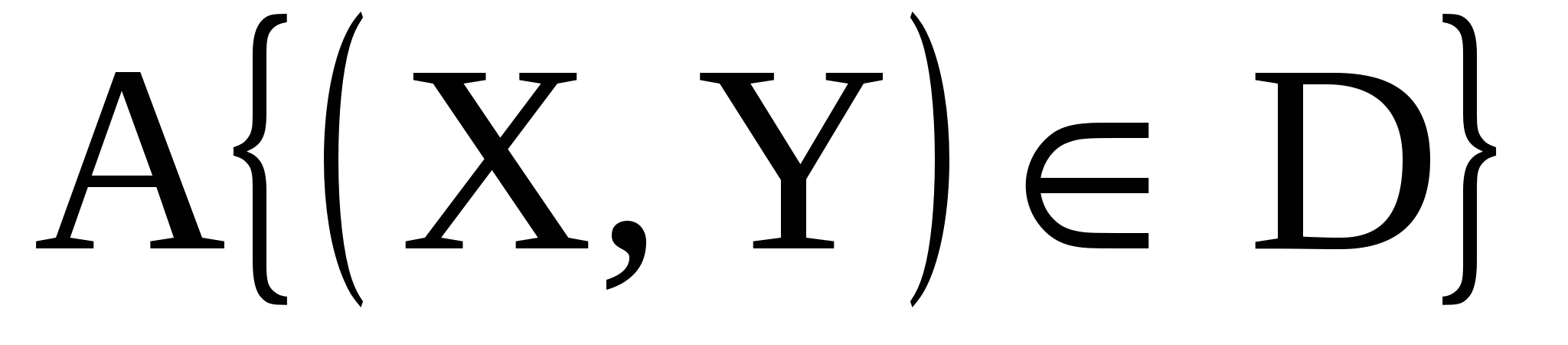 , где область , где область
D = {(x,y) / (0 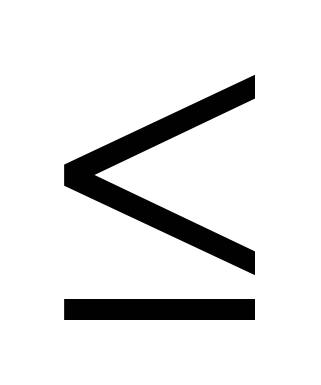 x x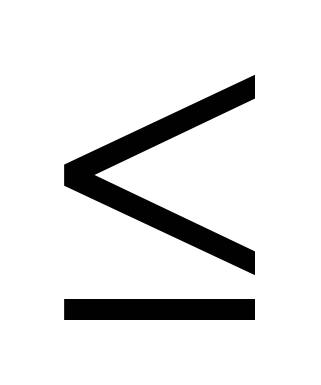 2, 0 2, 0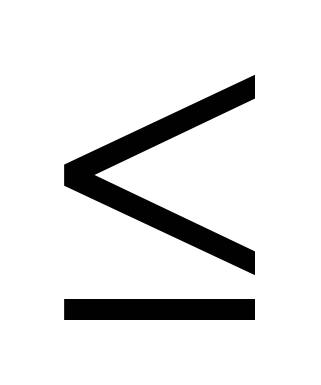 y y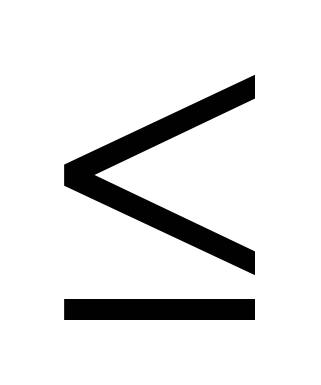 1); B = {X > Y}. 1); B = {X > Y}.
11.27. Случайная точка на плотности (X,Y) распределена по круговому нормальному закону (rxy = 0, x = y = = 1,) с центром рассеивания в начале координат. Вычислить вероятности следующих событий: A = {Y > X},
B = {Y> X}, C = {Y < 3X}, D = {X < 1}, E = {X < 1, Y < 2}.
11.28. Заданы следующие характеристики двумерного нормального вектора:
mx = -2; my = 3 и ковариационная матрица 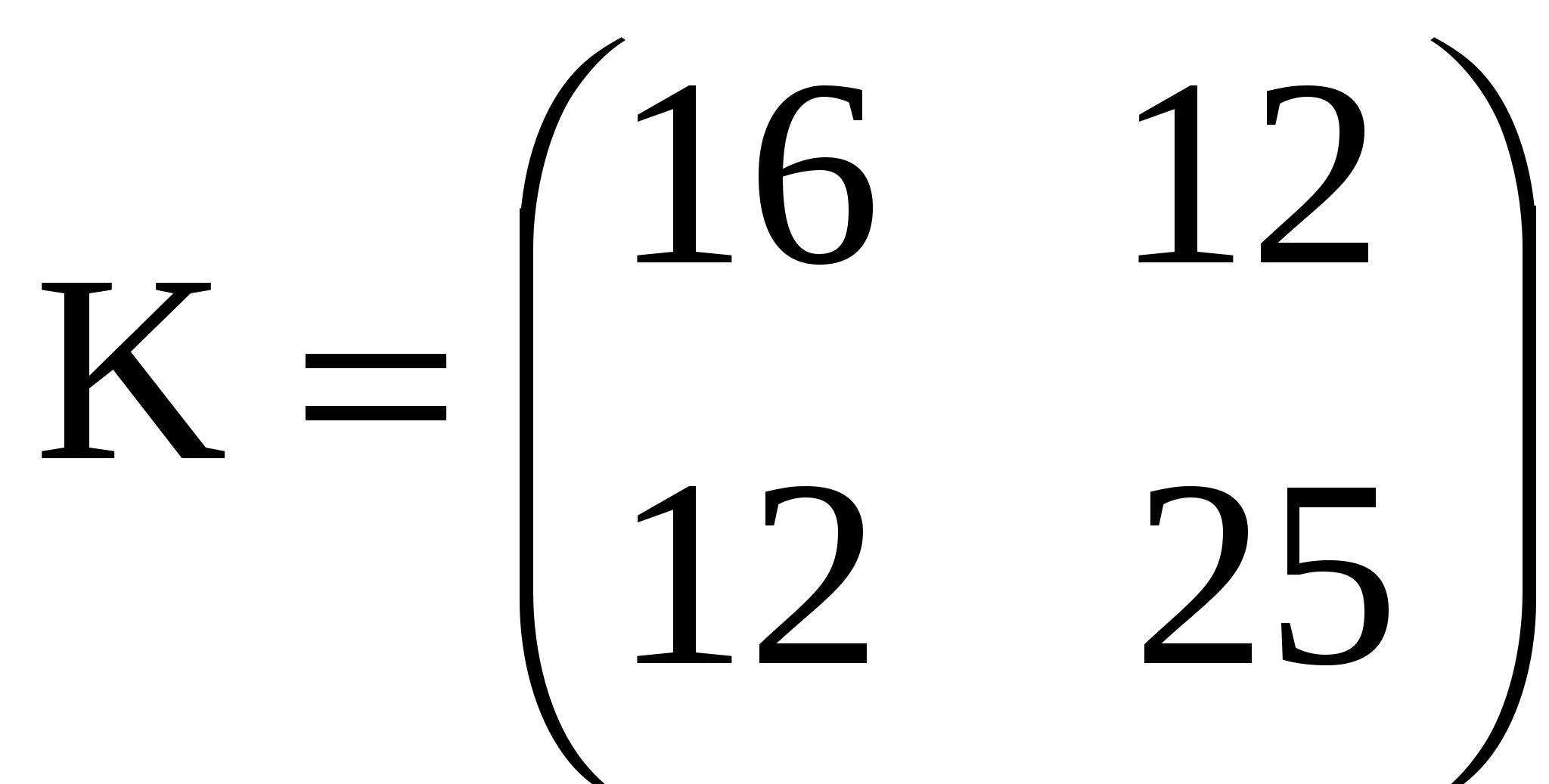 . Записать выражение для плотности распределения вероятностей f(x, y) и вычислить вероятность попадания в эллипс рассеивания с полуосями a = 2x, b = 2y. . Записать выражение для плотности распределения вероятностей f(x, y) и вычислить вероятность попадания в эллипс рассеивания с полуосями a = 2x, b = 2y.
11.29. Определить вероятность попадания точки с координатами (X, Y) в область, определяемую неравенствами (1 X 2, 1 Y 2), если функция распреде-ления 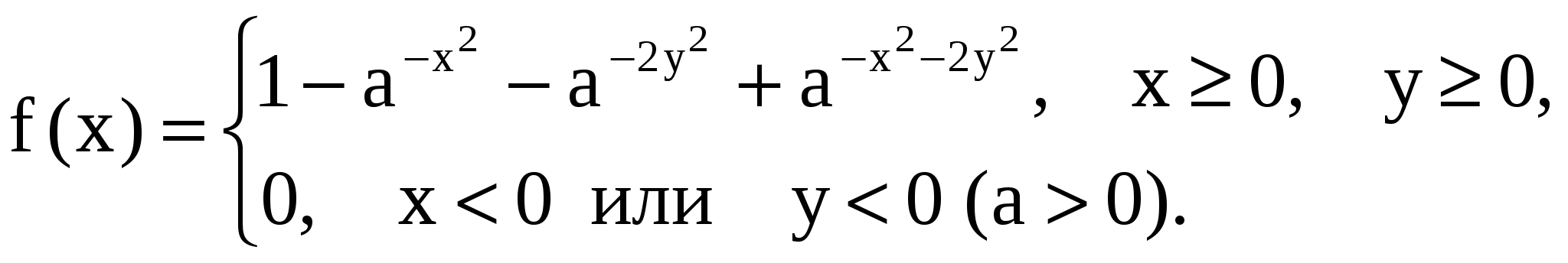
11.30. Определить математические ожидания и корреляционную матрицу системы случайных величин (X, Y), если плотность распределения вероятностей 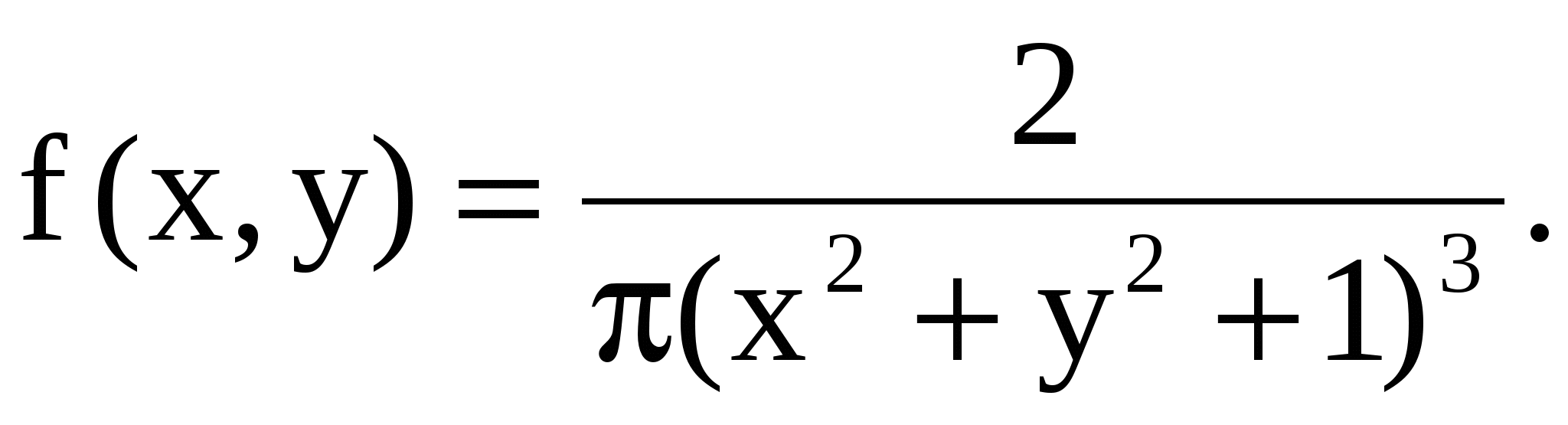
ОБРАЗЕЦ ВЫПОЛНЕНИЯ ЗАДАНИЯ
Задача 1. На рис. 1 и 2 изображены электрические схемы. Выключатели изображены кружками, в которых указан номер выключателя. Записать через события 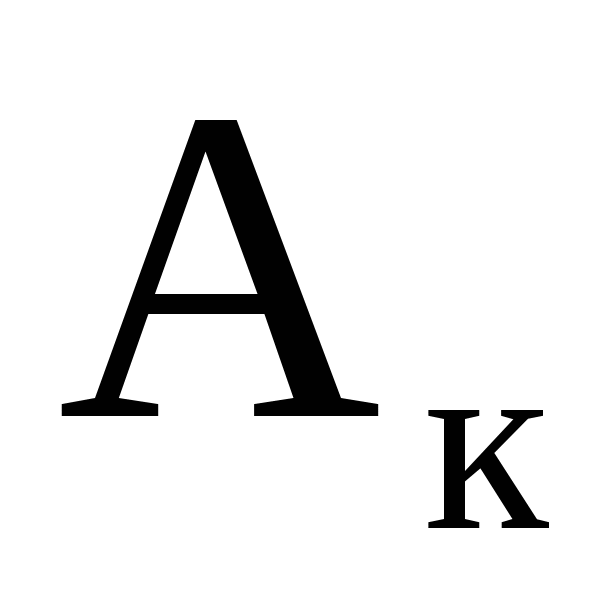 - «включен выключатель с номером - «включен выключатель с номером 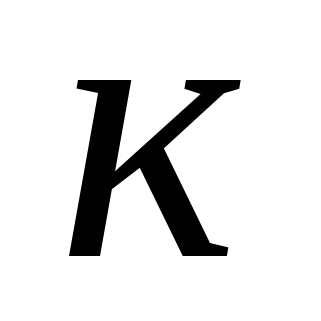 » для каждой схемы следующие события: » для каждой схемы следующие события:  - «ток идет» и - «ток идет» и  - «ток не идет». - «ток не идет».
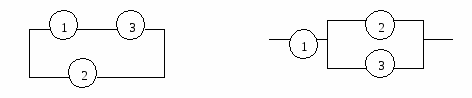
Рис. 1 Рис. 2
Решение. В схеме, приведенной на рис. 1, ток идет, если включены или 1 и 3 выключатели, или выключатель 2. Эти события соответственно равны 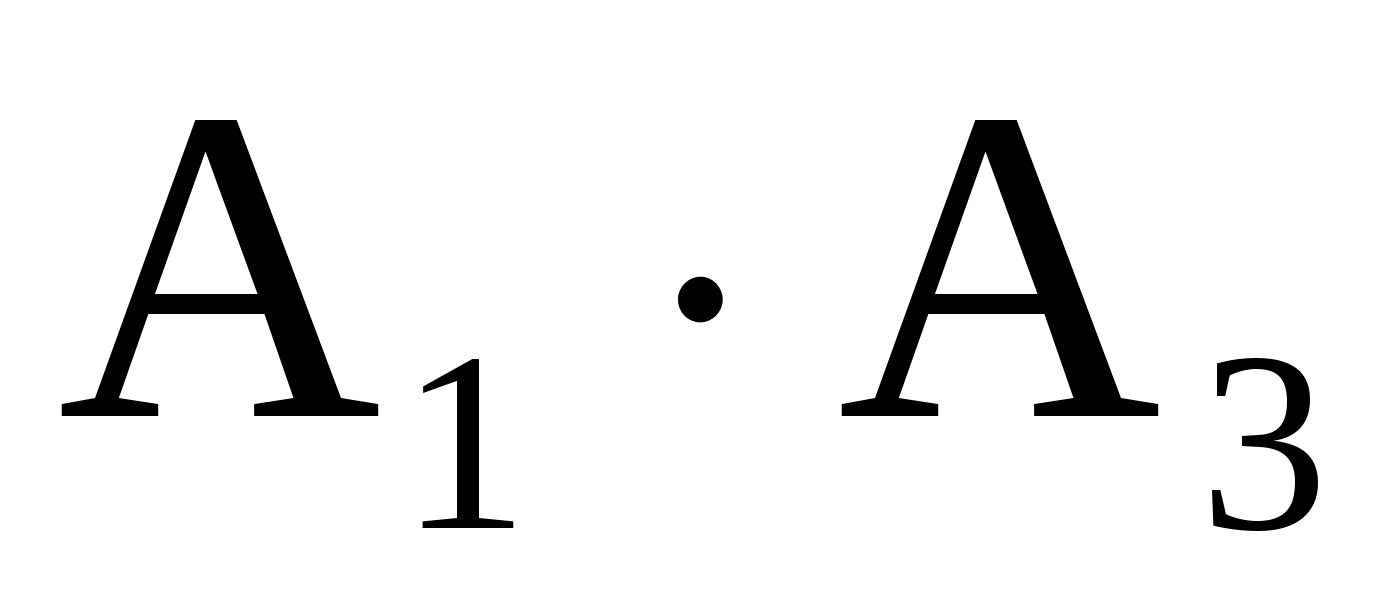 и и 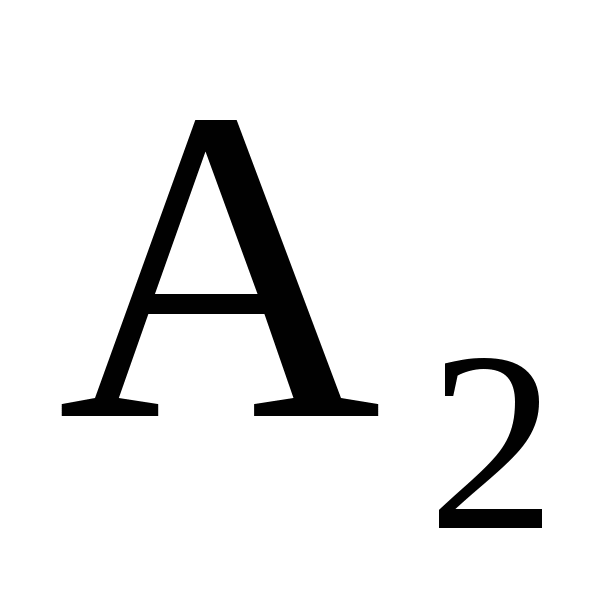 . Поэтому событие . Поэтому событие  . В схеме (рис. 1) ток не идет, если выключены выключатель 2 и хотя бы один из выключателей 1 или 3. Эти события соответственно равны . В схеме (рис. 1) ток не идет, если выключены выключатель 2 и хотя бы один из выключателей 1 или 3. Эти события соответственно равны 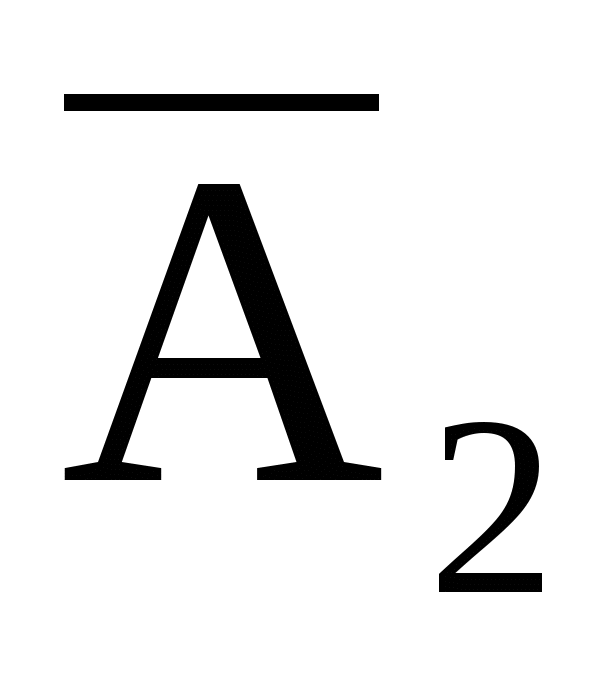 и и 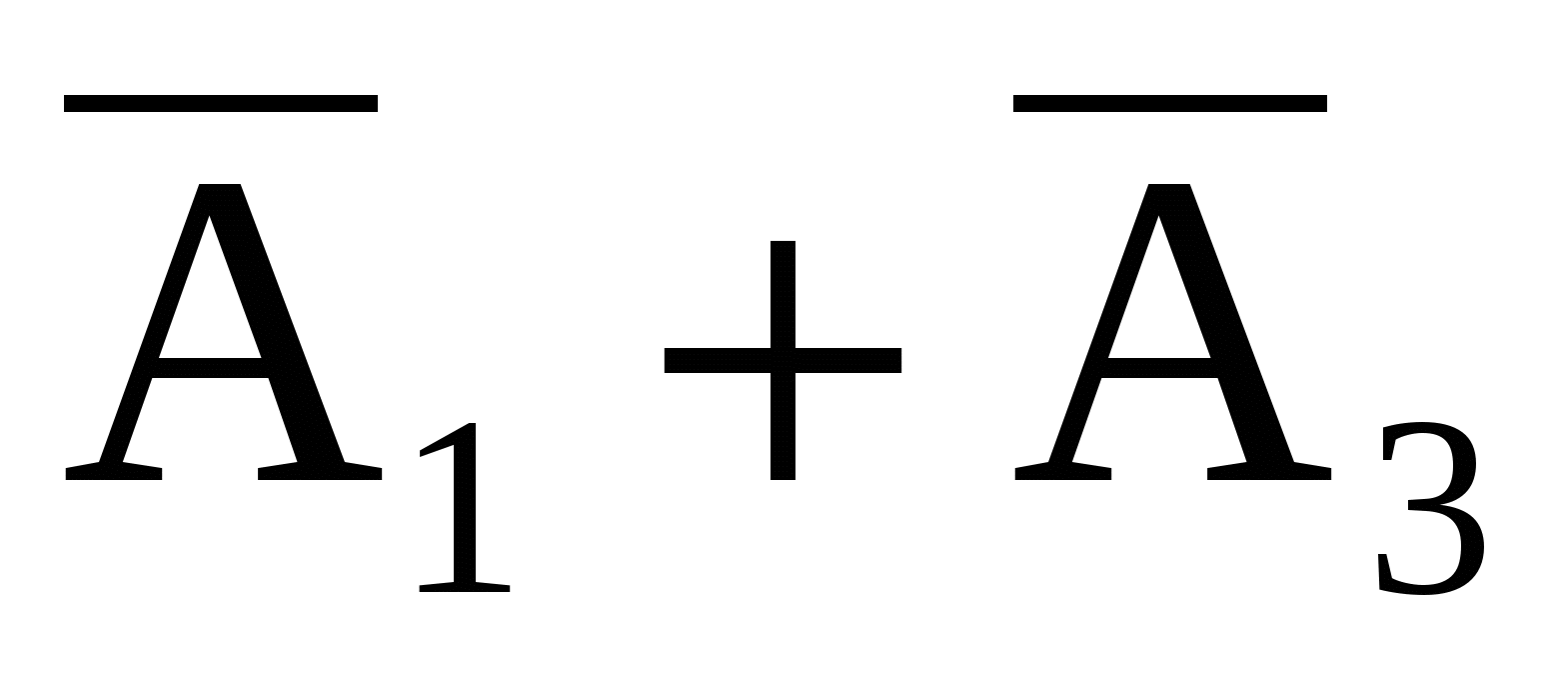 . Поэтому событие . Поэтому событие  . Иначе, используя свойства операций над событиями, . Иначе, используя свойства операций над событиями,
 . .
Для схемы (рис. 2) 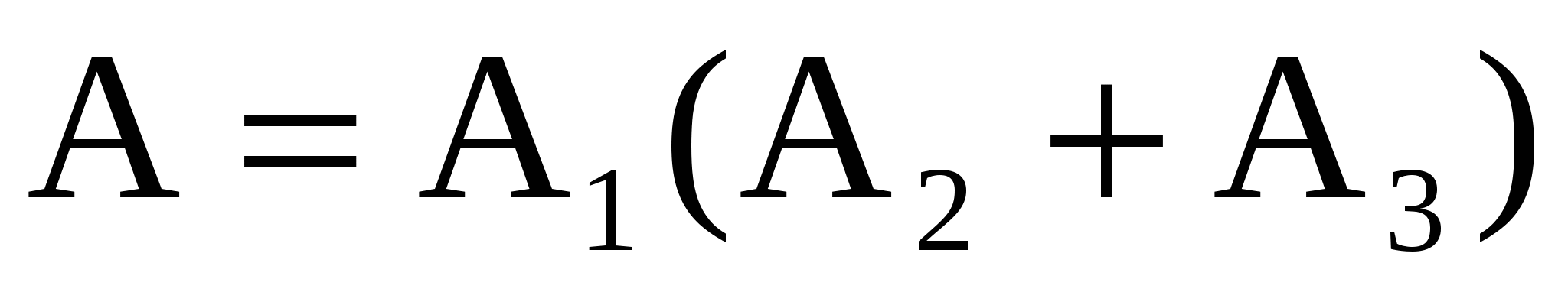 , , 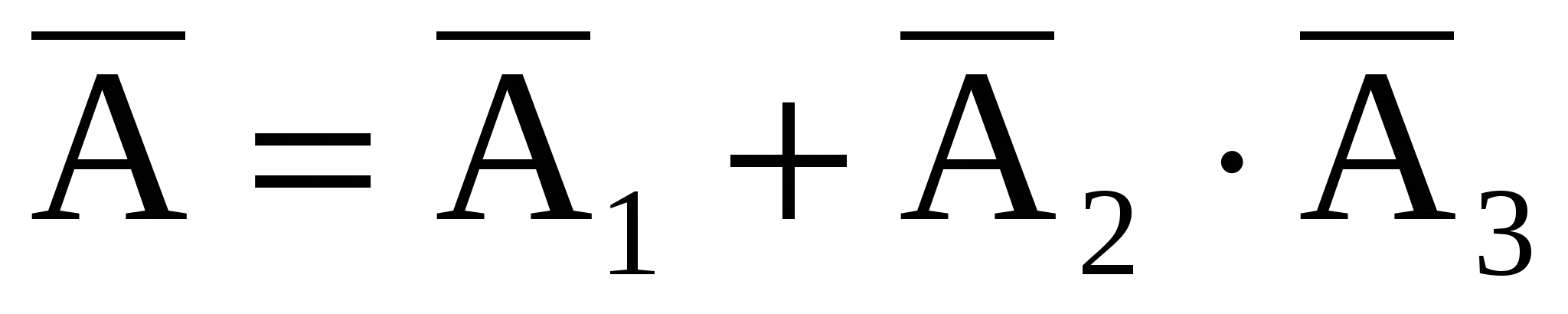 . .
Задача 2. Наудачу взятый телефонный номер состоит из пяти цифр. Как велика вероятность, что в нем: а) все цифры различные; б) все цифры нечетные?
Решение. а) Событие  - все цифры различные. - все цифры различные. 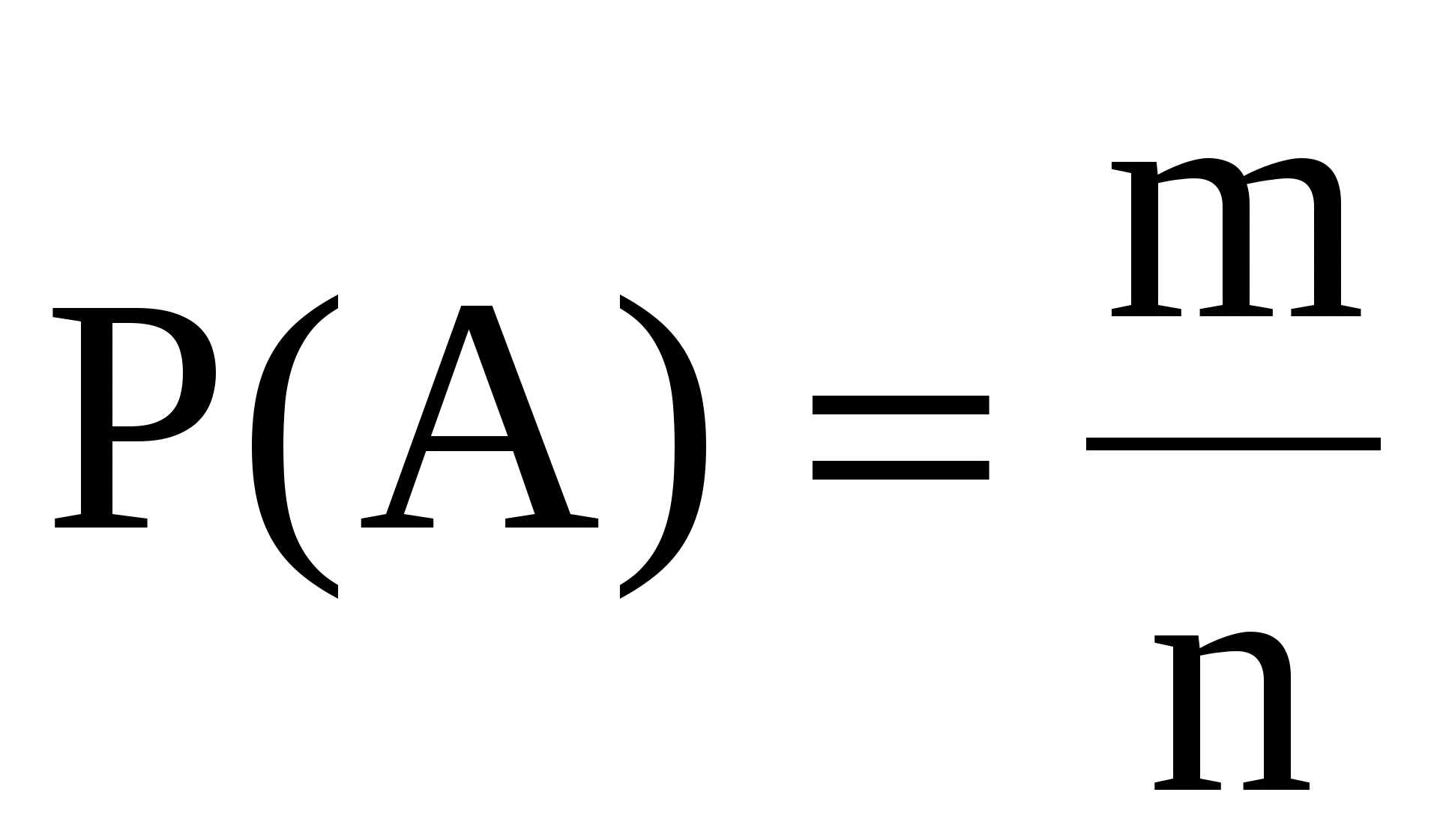 , где , где  - число всех элементарных равновозможных событий, m - число элементарных равновозможных событий, благоприятных наступлению события - число всех элементарных равновозможных событий, m - число элементарных равновозможных событий, благоприятных наступлению события  . Пусть . Пусть  - число всевозможных способов выбора 5 цифр из 10 возможных, причем цифры могут повторяться, поэтому - число всевозможных способов выбора 5 цифр из 10 возможных, причем цифры могут повторяться, поэтому 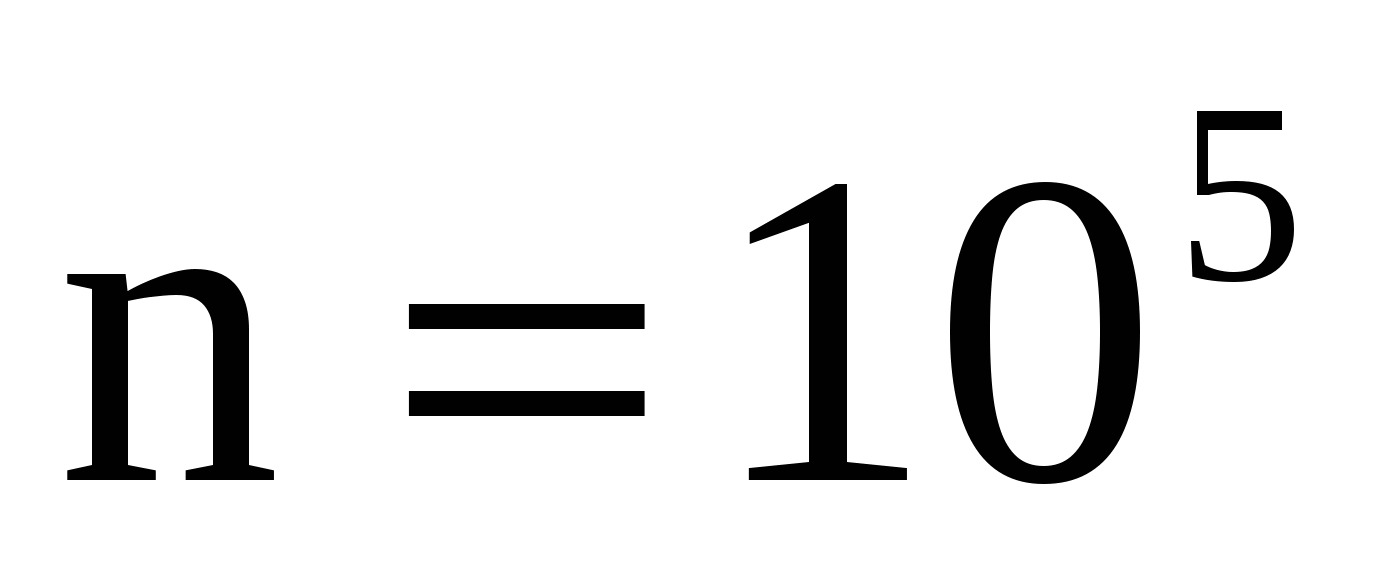 . m - число всевозможных способов выбора 5 цифр из 10 возможных, но цифры должны быть различными, поэтому . m - число всевозможных способов выбора 5 цифр из 10 возможных, но цифры должны быть различными, поэтому 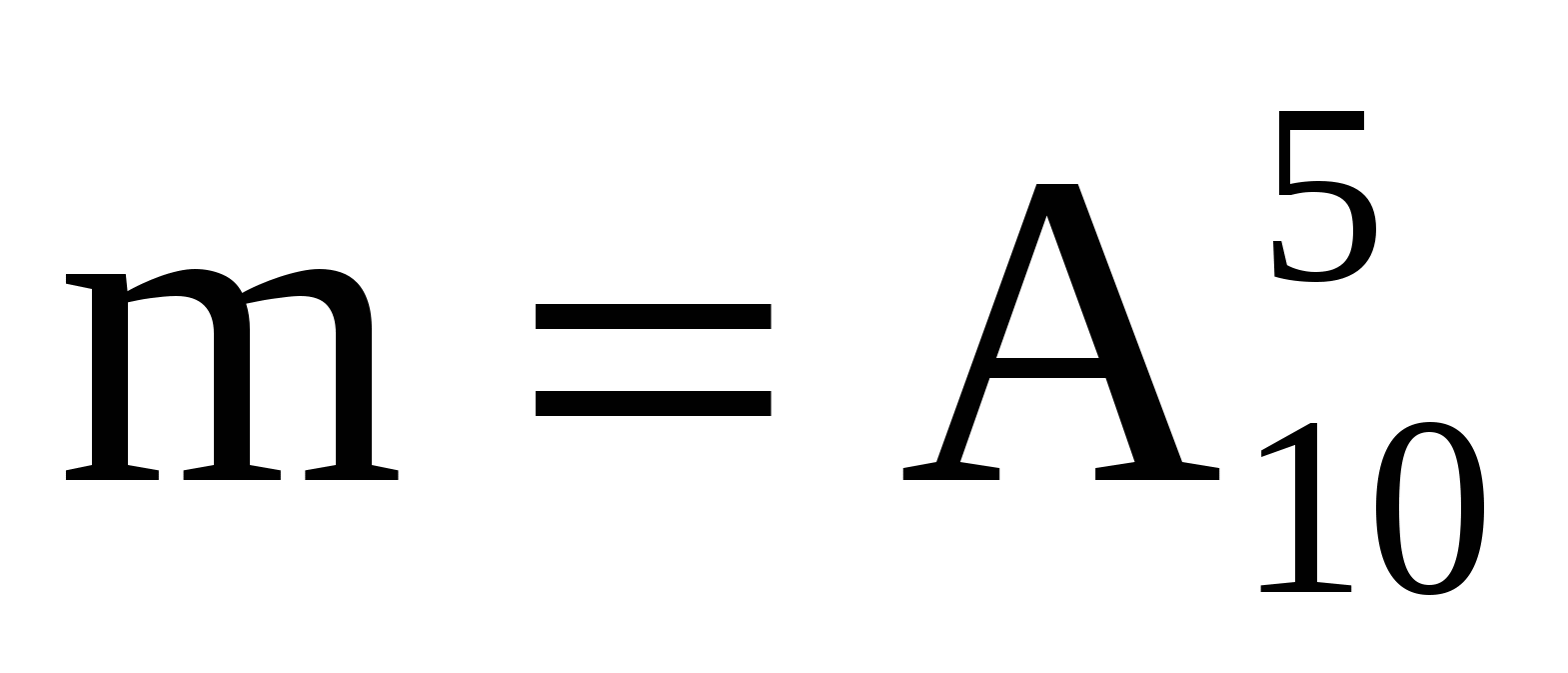 (порядок для телефонного номера важен). Таким образом, (порядок для телефонного номера важен). Таким образом, 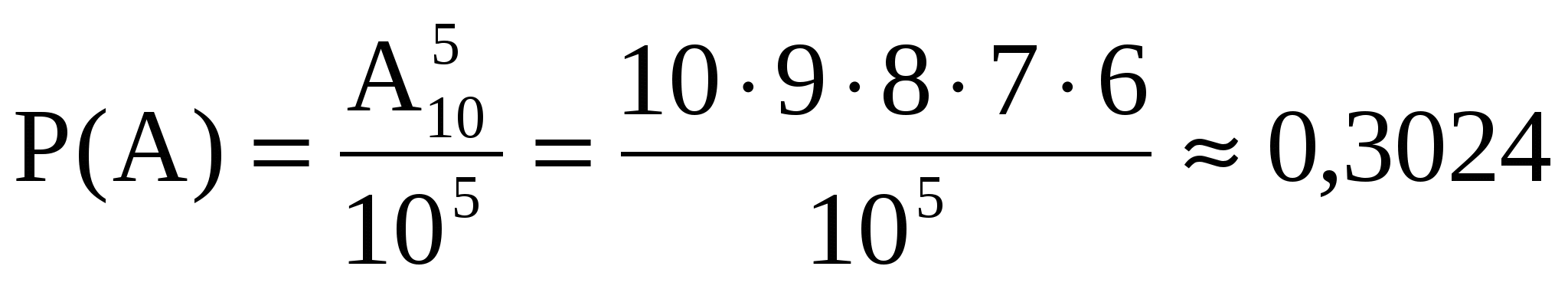 . .
б) Событие 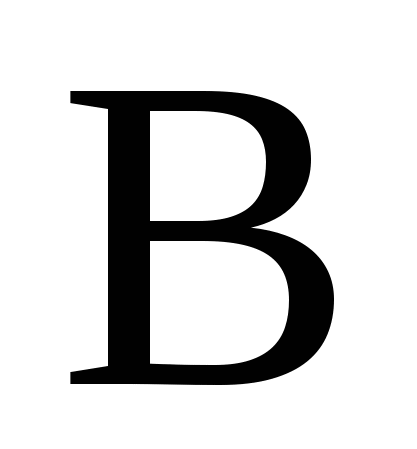 - все цифры нечетные. - все цифры нечетные. 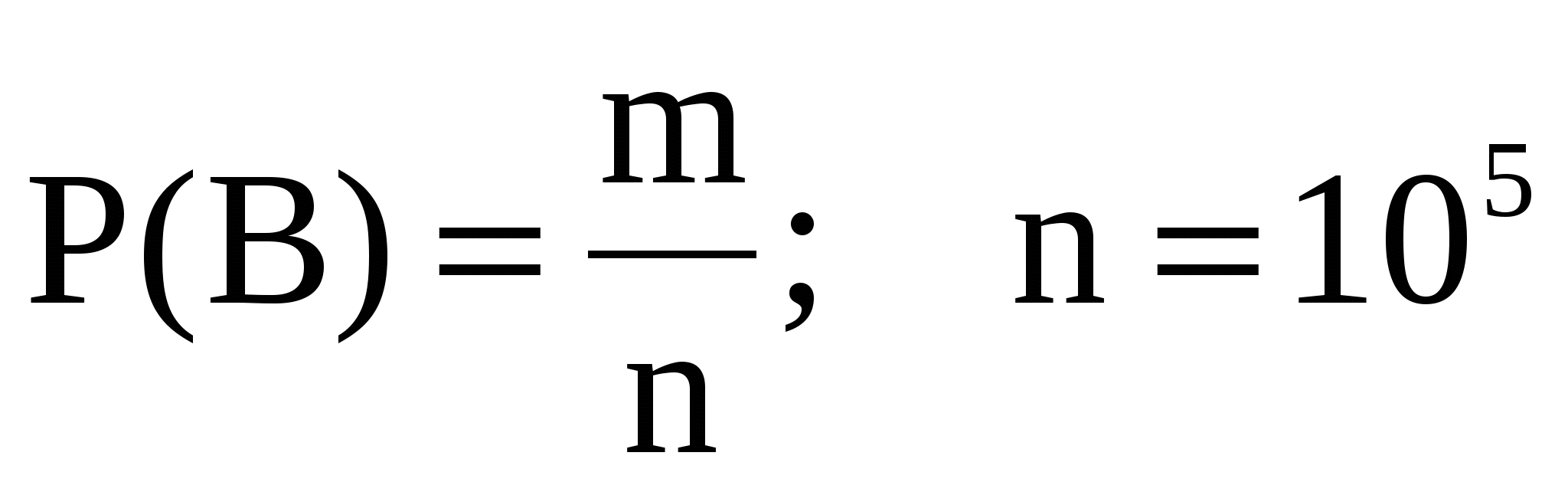 , , 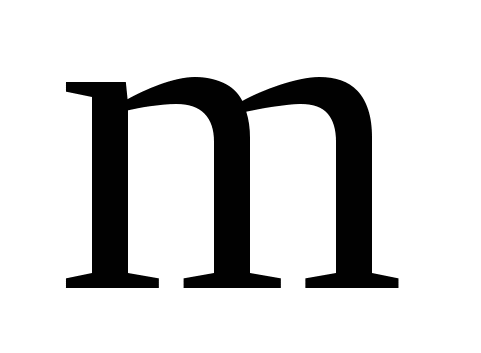 - число всевозможных способов выбора 5 цифр из 5 нечетных, причем цифры могут повторяться, поэтому - число всевозможных способов выбора 5 цифр из 5 нечетных, причем цифры могут повторяться, поэтому 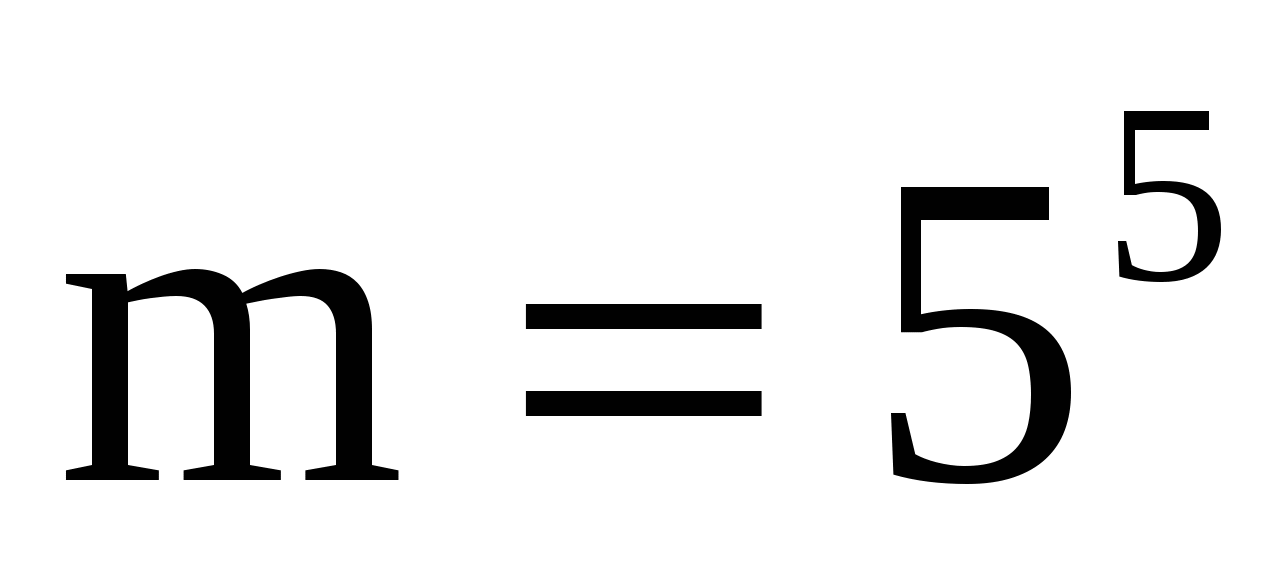 . Таким образом, . Таким образом, 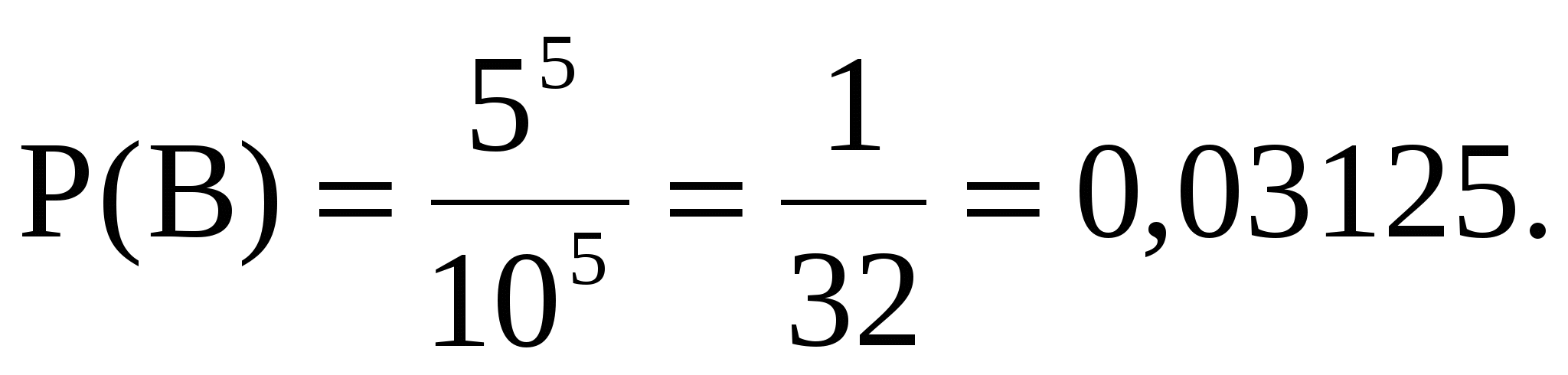
Задача 3. Некто написал 3 письма, запечатал их в конверты, а затем наудачу на каждом из них написал различные адреса. Определить вероятность того, что хотя бы на одном из конвертов написан правильный адрес.
Решение. Пусть событие 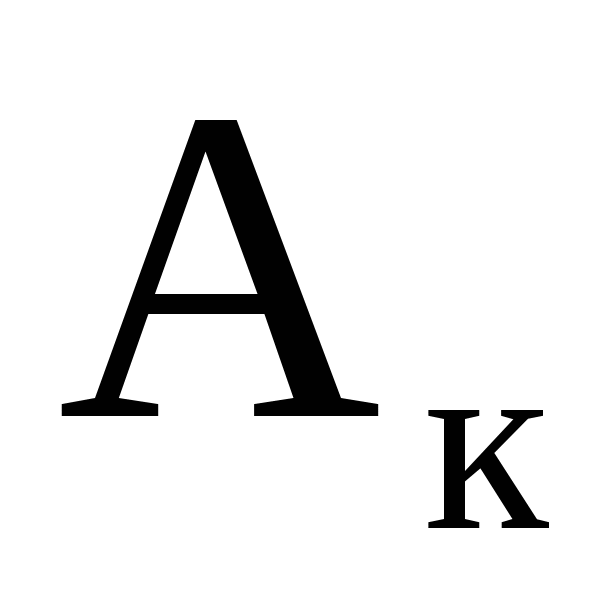 состоит в том, что на k-м конверте написан правильный адрес ( состоит в том, что на k-м конверте написан правильный адрес (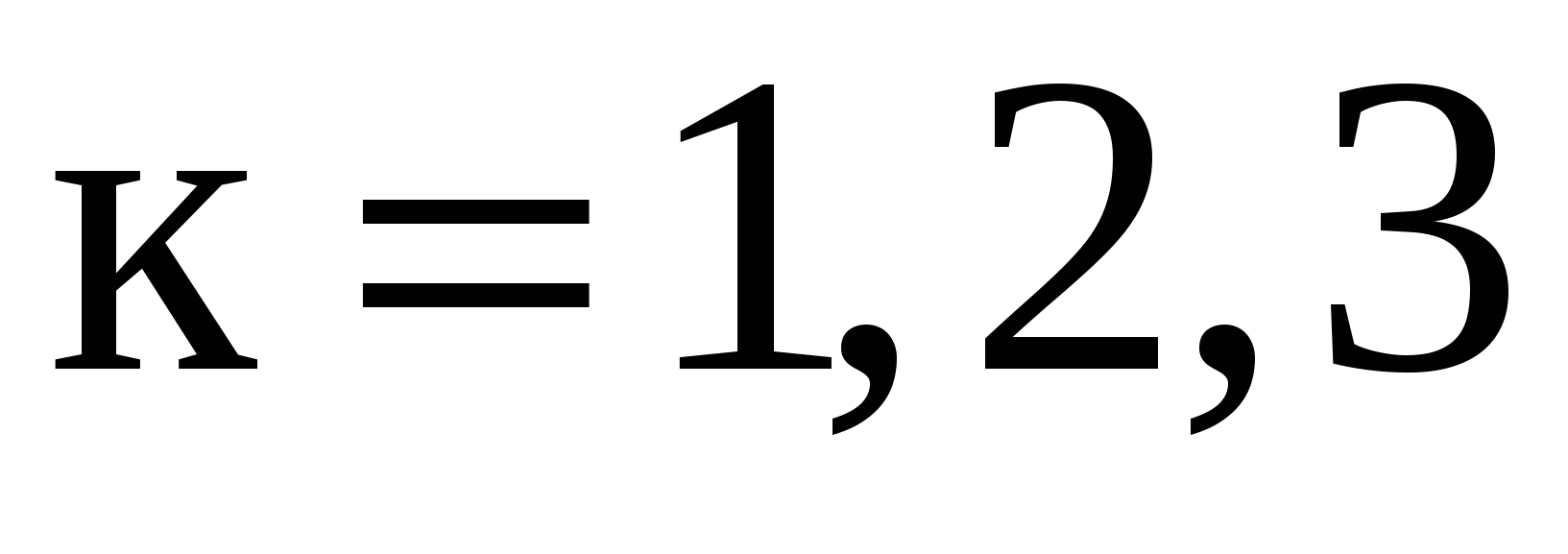 ). Искомая вероятность ). Искомая вероятность 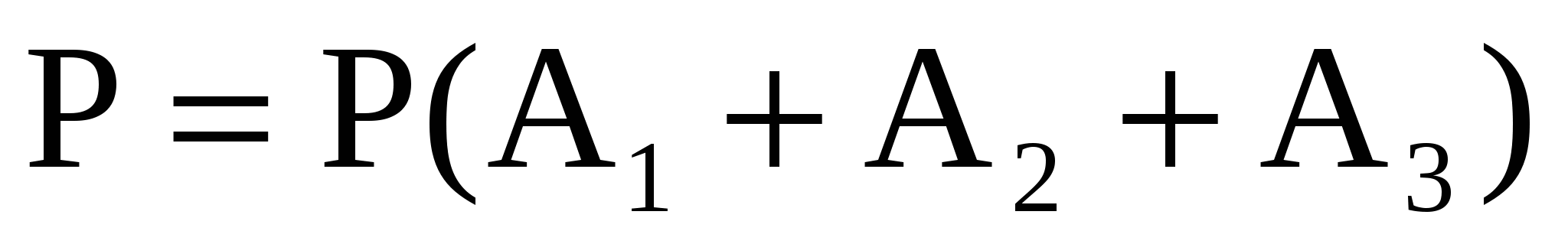 , так как события А1, А2, А3 совместны, то , так как события А1, А2, А3 совместны, то
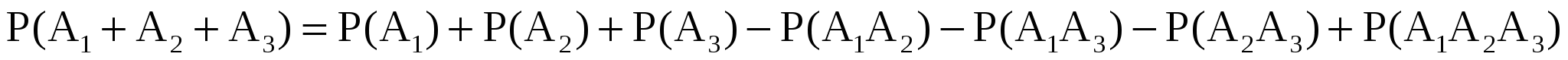 . .
Для всех 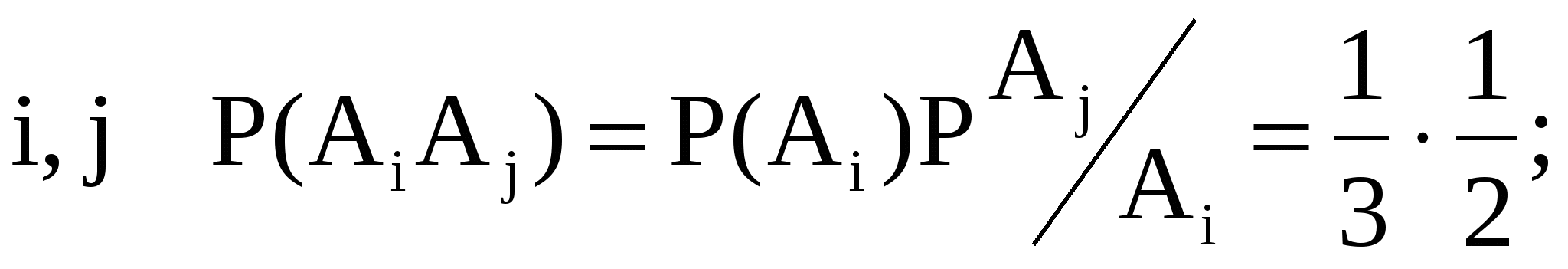 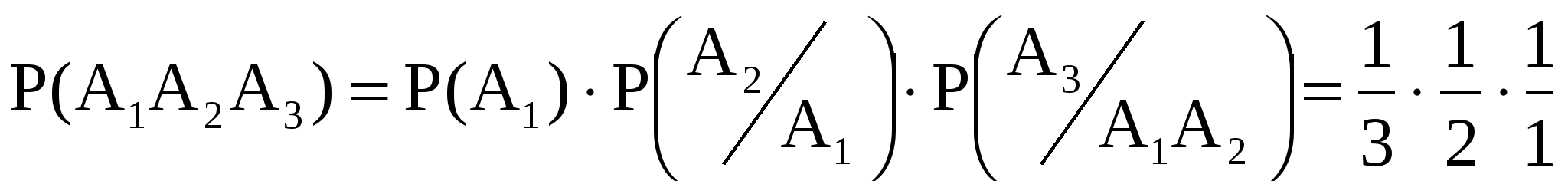 . Таким образом, . Таким образом,
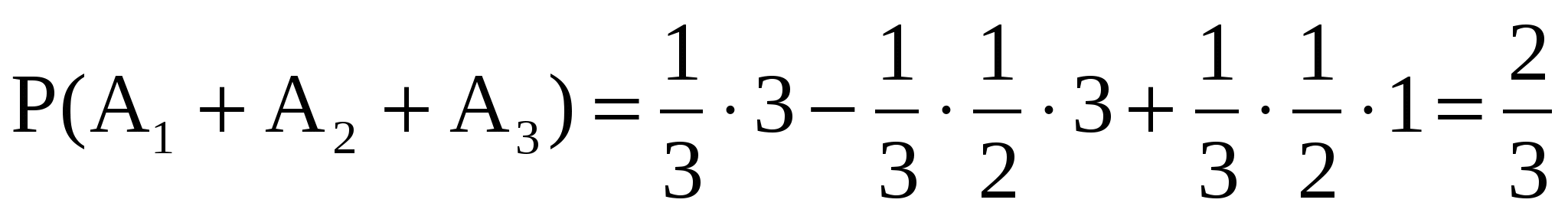 . .
Задача 4. Три станка подают детали в общий бункер. Вероятность выпуска бракованной детали для первого станка равна 0,03, для второго – 0,02 и для третьего – 0,01. Производительность первого станка в три раза больше производительности второго, а производительность третьего станка в два раза больше производительности второго. Какова вероятность того, что взятая наудачу из бункера деталь будет бракованной?
Решение. Пусть событие  - деталь, взятая наудачу из бункера, бракованная. Событие - деталь, взятая наудачу из бункера, бракованная. Событие  может произойти только совместно с одним из следующих событий: может произойти только совместно с одним из следующих событий:  - деталь изготовлена на 1-м станке, - деталь изготовлена на 1-м станке, 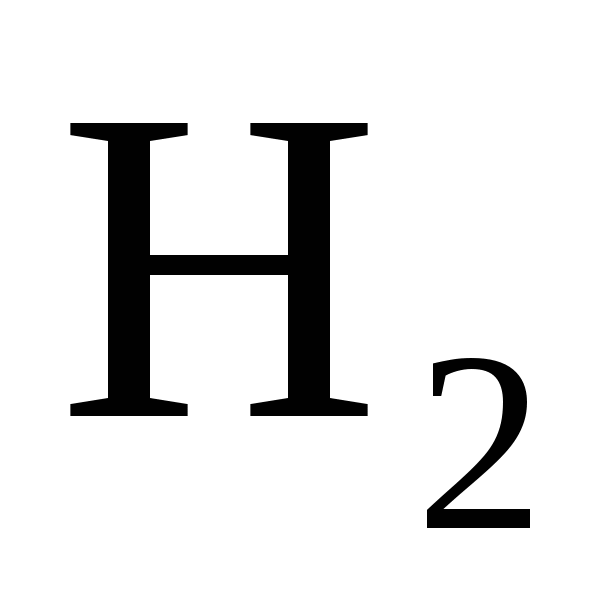 - на 2-м станке, - на 2-м станке,  - на 3-м станке. События - на 3-м станке. События 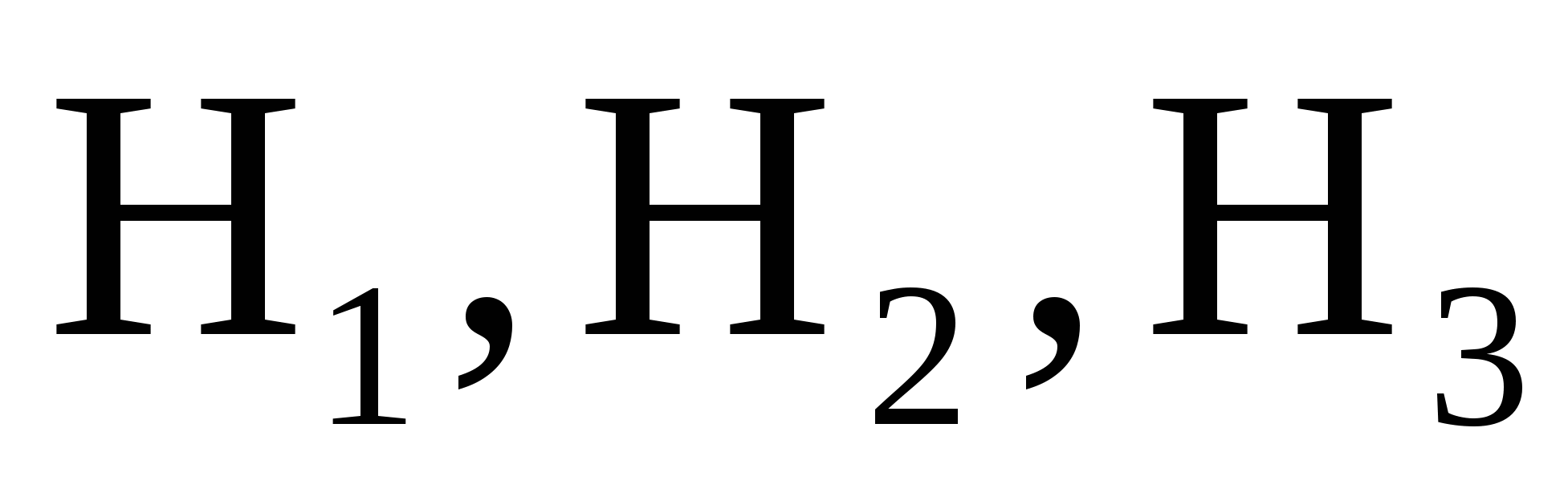 образуют полную группу несовместных событий, поэтому образуют полную группу несовместных событий, поэтому
 . Если принять производительность второго станка за k, то производительность первого станка - 3k, третьего – 2k. Тогда . Если принять производительность второго станка за k, то производительность первого станка - 3k, третьего – 2k. Тогда 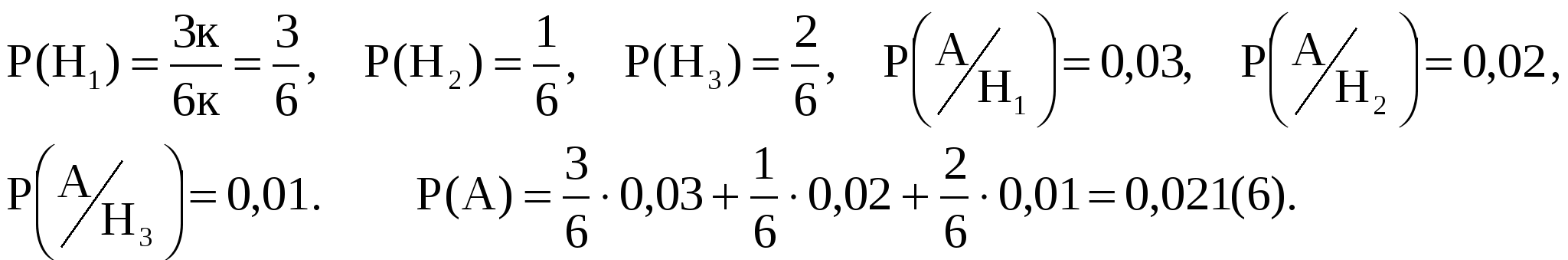 
Задача 5. Найти вероятность того, что среди 200 изделий окажется более трех бракованных, если в среднем бракованные изделия составляют 1%.
Решение. Пусть событие  - бракованных изделий окажется более трех. - бракованных изделий окажется более трех.
 - бракованных изделий не более трех. - бракованных изделий не более трех.
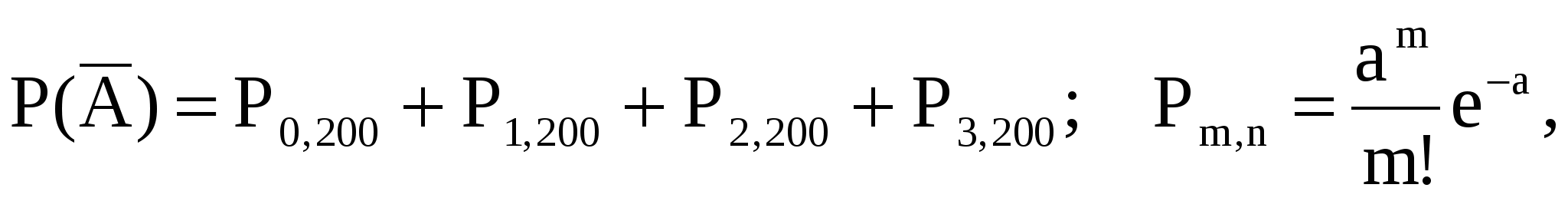 где где 
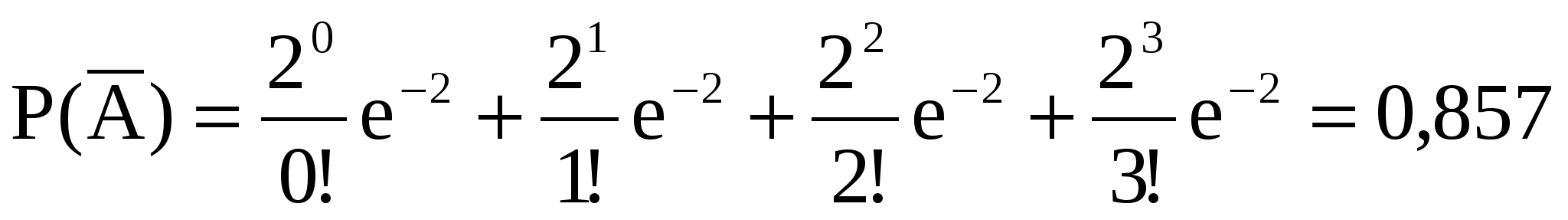 . .
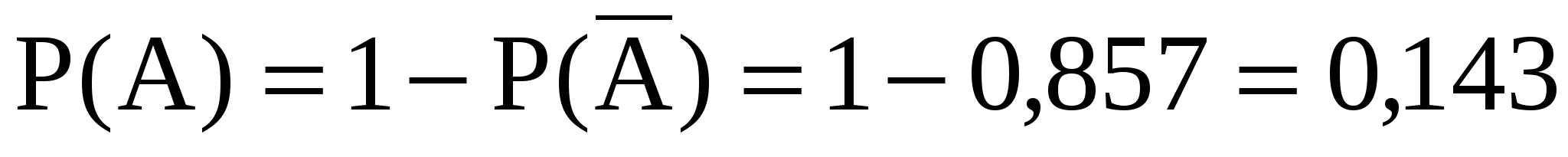 . .
Задача 6. Производится два независимых выстрела по мишени. Вероятность попадания при каждом выстреле равна 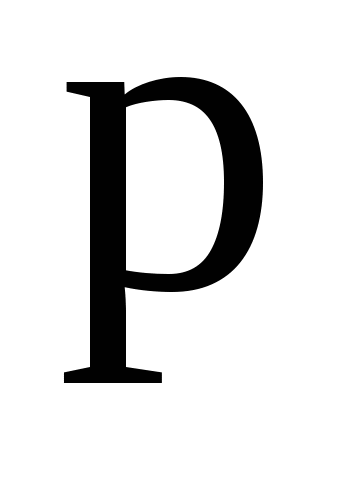 . Рассматриваются случайные величины: . Рассматриваются случайные величины:
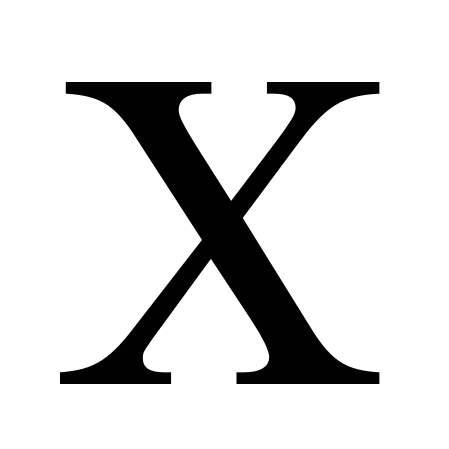 - разность между числом попаданий и числом промахов; - разность между числом попаданий и числом промахов;  - сумма числа попаданий и числа промахов. Построить для каждой из случайных величин - сумма числа попаданий и числа промахов. Построить для каждой из случайных величин 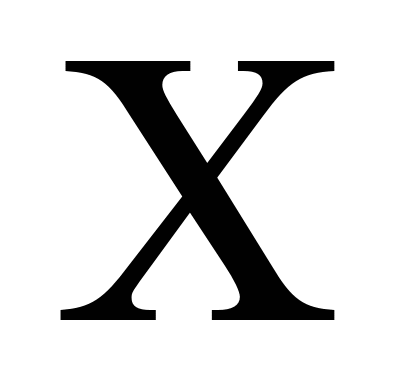 , , ряд распределения. Найти их характеристики ряд распределения. Найти их характеристики 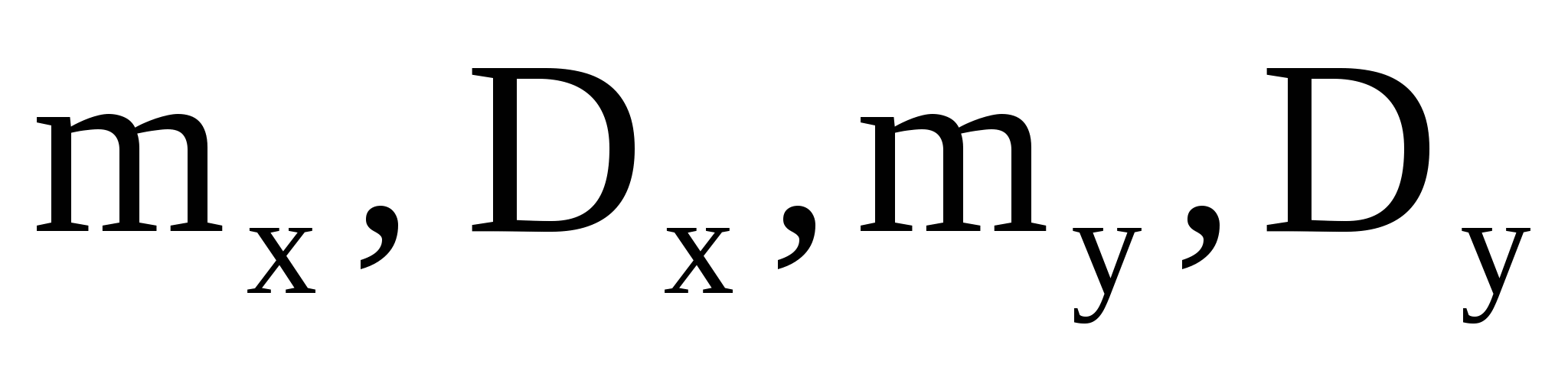 . .
Решение. Случайная величина 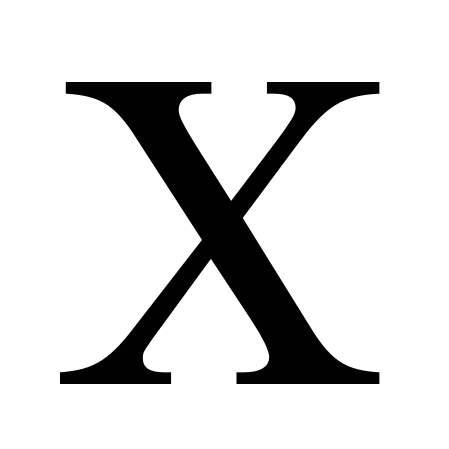 может принимать следующие значения: может принимать следующие значения: 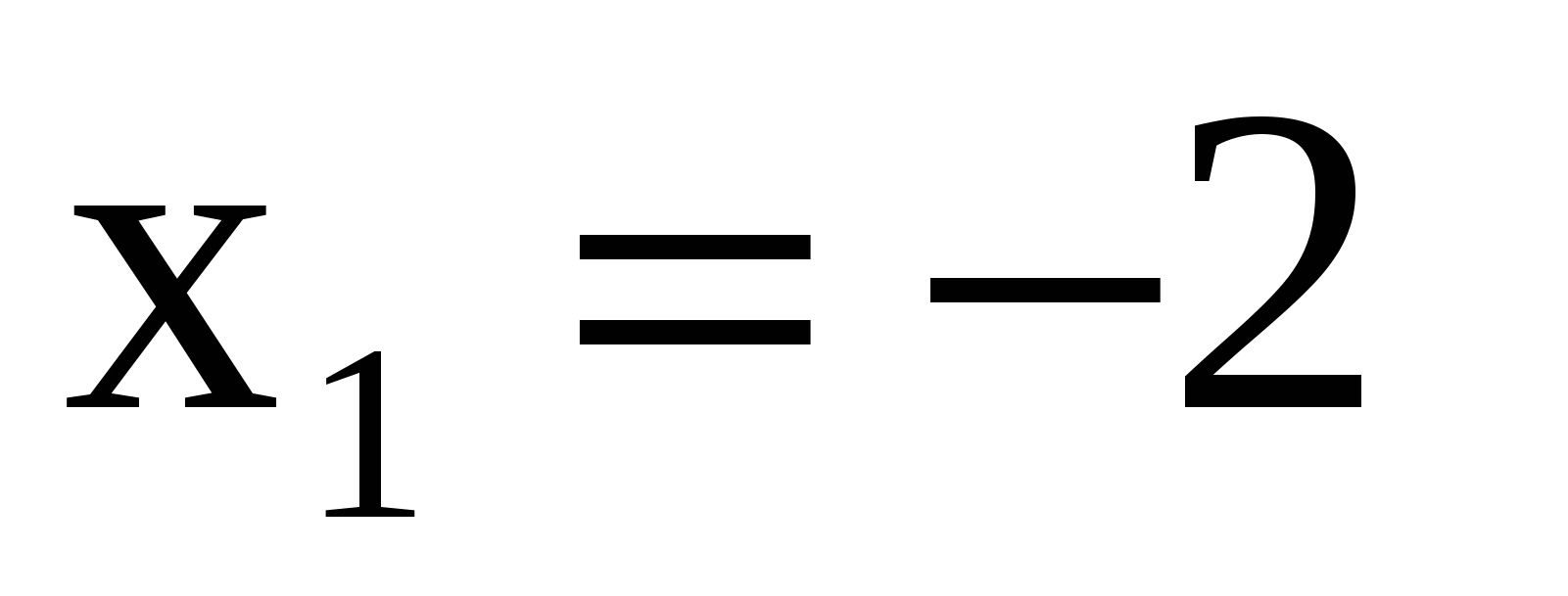 (0 попаданий, 2 промаха), (0 попаданий, 2 промаха), 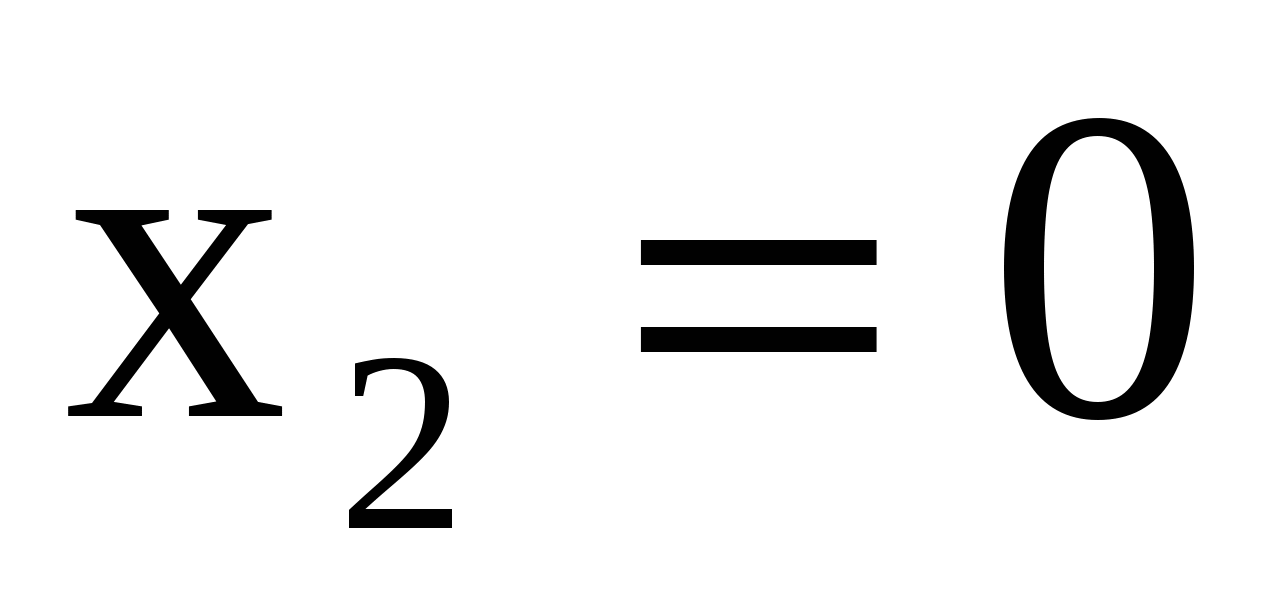 (1 попадание, 1 промах), (1 попадание, 1 промах), 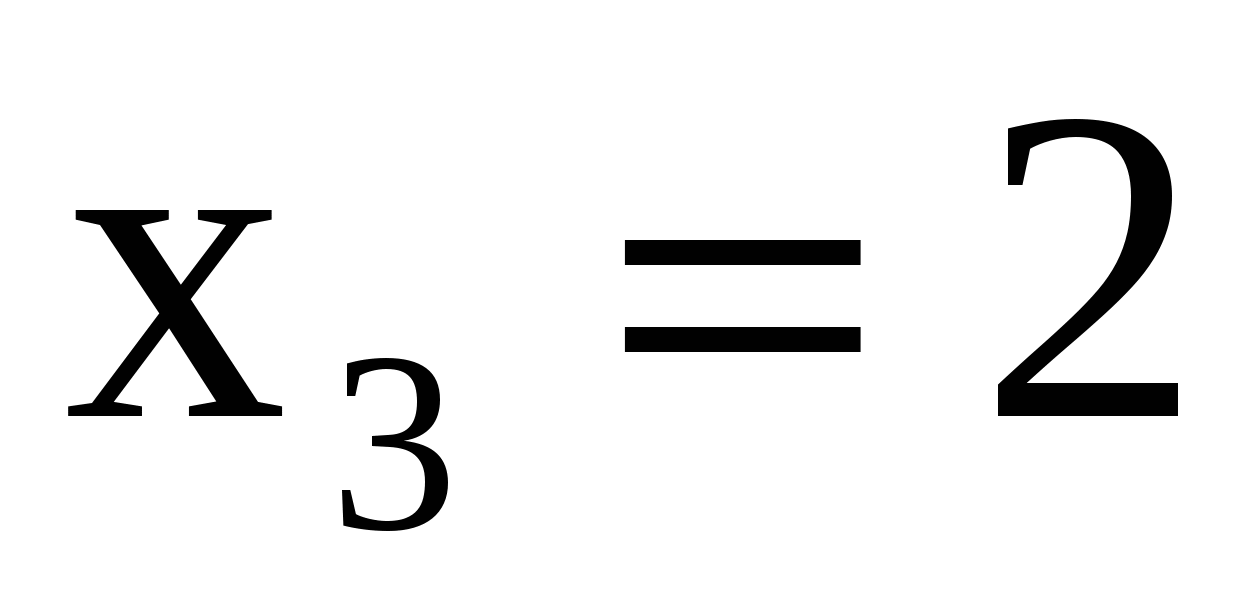 (2 по-падания, 0 промахов). Вероятности значений случайной величины (2 по-падания, 0 промахов). Вероятности значений случайной величины 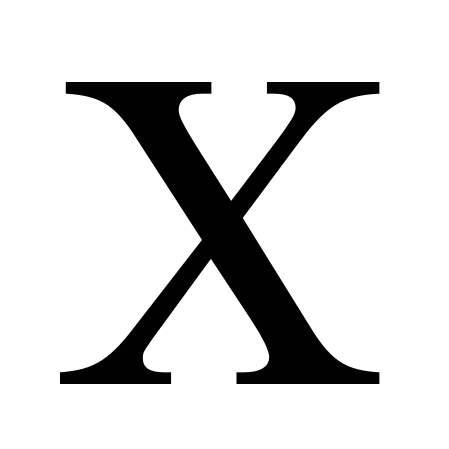 находятся по формуле Бернулли: находятся по формуле Бернулли: 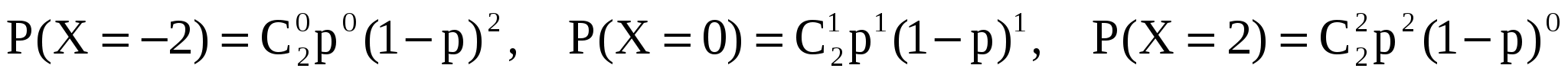 . .
Ряд распределения будет иметь вид
|
|
|
 Скачать 1.2 Mb.
Скачать 1.2 Mb.