Теория вероятностей. Задача 1 Пусть а в. Упростить выражения а в, АВ, а в с, АВС

• Название: Задача 1 Пусть а в. Упростить выражения а в, АВ, а в с, АВС
• Анкор: Теория вероятностей.doc
• Дата: 27.05.2017
• Размер: 1.2 Mb.
• Имя файла: Теория вероятностей.doc
• Тип: Задача; #8060
• страница: 5 из 7

A

_{0 1 3} x
1) Найти A и написать выражение плотности. 2) Найти и построить график функции распределения F(x). 3) Вычислить математическое ожидание и дисперсию.

8.21. Вероятность отказа детали за время испытания на надежность равна 0,2. Найти среднее число отказавших деталей, если испытанию будут подвергнуты 10 деталей.

8.22. Время безотказной работы элемента распределено по показательному закону при t0 (t - время в часах). Найти вероятность того, что элемент проработает безотказно 100 ч.

8.23. Известно, что в партии из 20 телефонных аппаратов имеется 5 неисправных. Из партии выбрано 4 аппарата. Найти закон распределения, математическое ожидание и дисперсию числа неисправных аппаратов среди отобранных.

8.24. По известному "правилу трех сигм" вероятность отклонения случайной величины от своего математического ожидания более чем на три корня из дисперсии мала. Найти если Х имеет: а) нормальное распре-

деление; б) показательное распределение.

8.25. По известному "правилу трех сигм" вероятность отклонения случайной величины от своего математического ожидания более чем на три корня из дисперсии мала. Найти если Х имеет: а) нормальное распреде-ление, б) равномерное на отрезке

8.26. По известному "правилу трех сигм" вероятность отклонения случайной величины от своего математического ожидания более, чем на три корня из дисперсии мала. Найти если Х распределена: а) нормально;

б) по закону Пуассона с .

8.27. Для случайной величины Х, распределенной по закону Пуассона, вычислить , математическое ожидание и дисперсию, если параметр а = 0,3; k = 2.

8.28. Все значения равномерно распределенной случайной величины лежат на отрезке . Найти вероятность попадания значений случайной величины в промежуток .

8.29. Трамваи данного маршрута городского трамвая идут с интервалом 5 мин. Пассажир подходит к трамвайной остановке в некоторый момент времени. Какова вероятность появления пассажира не ранее чем через минуту после ухода предыдущего поезда, но не позднее, чем за две минуты до отхода следующего поезда?

8.30. Определить постоянную вероятность попадания в цель при каждом выстреле и число произведенных выстрелов, если среднее число попаданий рав-

но 72, а среднее квадратическое отклонение случайной величины, характеризу-ющей число попаданий, равно 6.
Задача № 9.

9.1. Производится измерение диаметра вала без систематических (одного знака) ошибок. Случайные ошибки измерения X подчинены нормальному закону со средним квадратическим отклонением = 10 мм. Найти вероятность того, что измерение будет произведено с ошибкой, не превосходящей по абсолютной величине 15 мм.

9.2. Измерение дальности до объекта сопровождается систематическими и случайными ошибками. Систематическая ошибка равна 50 м в сторону занижения дальности. Случайные ошибки подчиняются нормальному закону со средним квадратическим отклонением = 100 м. Найти: 1) вероятность измерения даль-ности с ошибкой, не превосходящей по абсолютной величине 150 м; 2) вероятность того, что измеренная дальность не превзойдет истинной.

9.3. Определить среднее квадратическое отклонение случайной ошибки прибора, если систематических ошибок он не имеет, а случайные распределены по нормальному закону и с вероятностью 0,8 не выходят за пределы 20 м.

9.4. Случайная величина X подчинена нормальному закону распределения с параметрами а = -1, = 2. Определить вероятность неравенства -2 < X < 1. Построить график плотности распределения.

9.5. На автомате изготавливаются заклепки. Диаметр их головок пред-ставляет собой случайную величину, распределенную по нормальному закону, и имеет среднее значение, равное 2 мм, и дисперсию, равную 0,01. Какие размеры диаметра головок заклепки можно гарантировать с вероятностью 0,95?

9.6. Случайная величина X распределена по нормальному закону с парамет-рами a = 30, = 10. В какой интервал с вероятностью практической достоверности 0,997 попадут значения случайной величины X?

9.7. Автомат изготавливает шарики. Шарик считается годным, если отклонение Х диаметра шарика от проектного размера по абсолютной величине меньше 0,7 мм. Считая, что случайная X величина распределена нормально со средним квадратическим отклонением = 0,4 мм, найти, сколько будет готовых шариков среди 100 изготовленных.

9.8. Случайная величина Х подчинена нормальному закону распределения с плотностью Определить вероятность того, что случайная величина Х примет значение, не меньшее 0 и не больше 12.

9.9.Случайная величина Х подчинена нормальному закону распределения с параметрами Написать выражение для плотности распределения и функции распределения этой случайной величины. Построить график функции распределения.

9.10. Длина изготовляемой автоматом детали представляет собой случайную величину, распределенную по нормальному закону с параметрами см, см. Найти вероятность брака, если допустимые размеры детали должны быть 15 0,3 см. Какую точность изготовляемой автоматом детали можно гаран-тировать с вероятностью 0,97?

9.11. При взвешивании тела установлен средний вес 2,36 г и среднее квадратическое отклонение веса 0,025 г. Вес – случайная величина Х, распреде-ленная нормально. Найти: а) какой процент значений находится между 2,3 г и 2,4 г; б) какую точность взвешивания можно гарантировать с вероятностью 0,97?

9.12. Размер диаметра втулок, изготовляемых цехом, можно считать нормаль-но распределенной случайной величиной с математическим ожиданием 2,5 см и дисперсией 0,0001 см², в каких границах можно практически гарантировать размер диаметра втулки, если за вероятность практической достоверности принимается 0,997?

9.13. На стенке изготовляются детали заданной длины. Установлено, что

60 % деталей отклоняются от заданной длины не более чем на 2 мм (в обе стороны). Какой процент деталей будет отклоняться от заданной длины не более чем на 5 мм, если предполагается, что величина отклонения есть случайная величина, распределенная по нормальному закону?

9.14. Бомбардировщики сбросили бомбы на мост длиной 60 м и шириной 12 м. Рассеивание попаданий происходит по нормальному закону с дисперсией, равной 225 м² по длине и 36 м² по ширине, средняя точка попаданий - центр моста. Рассеивания по длине и ширине независимы. Найти вероятность попадания в мост при сбрасывании одной бомбы.

9.15. Стрельба ведется от точки Х вдоль прямой ОХ. Средняя дальность полета «а». Предполагается, что дальность полета распределена по нормальному закону со средним квадратическим отклонением 80 м. Найти, какой процент выпускаемых снарядов дает перелет от 120 м до 160 м.

9.16. Случайная величина X подчинена нормальному закону с параметрами а, . Вычислить с точностью до 0,01 вероятность попадания значений случайной величины X в интервал (а; а+) (без использования таблиц функции Лапласа).

9.17. Считается, что отклонение длины изготовляемых деталей от стандарта является случайной величиной, распределенной по нормальному закону. Если стандартная длина равна 40 см и среднее квадратическое отклонение равно 0,4 см, то какую точность длины изделия можно гарантировать с вероятностью 0,8?

9.18. Пусть вес пойманной рыбы подчиняется нормальному закону. Параметры его следующие: cреднее квадратическое отклонение математическое ожидание а = 375 г. Найти вероятность того, что вес пойманной рыбы будет заклю-чен в границах от 300 г до 425 г.

9.19.Пусть диаметр изготовляемой детали является случайной величиной, распределенной по нормальному закону. Математическое ожидание ее а = 4,5 см, а среднее квадратическое отклонение = 0,05 см. Найти вероятность того, что размер диаметра взятой наудачу детали отличается от математического ожидания не более чем на 1 мм.

9.20. Среднее квадратическое отклонение случайной величины, распределенной по нормальному закону, равно 2 см, а математическое ожидание равно 16 см. Най-ти границы, в которых с вероятностью 0,95 следует ожидать значение случайной величины.

9.21. Найти дисперсию случайной величины, распределенной по нормальному закону, если известно, что отклонения от математического ожидания, не превосходящие 0,1 см, имеют место с вероятностью 0,7887.

9.22. Станок-автомат изготавливает валики, причем одновременно контролирует их диаметр Х. Считая, что Х - нормально распределенная случайная величина с математическим ожиданием 10 мм и средним квадратическим отклонением

 = 0,1 мм, найти интервал, в котором с вероятностью 0,9973 будут заключены диаметры изготовленных валиков.

9.23. Плотность распределения вероятностей случайной величины Х имеет вид Найти: 1) ; 2) математическое ожидание , дисперсию ; 3) вероятность выполнения неравенства .

9.24. Случайная величина X имеет нормальное распределение с математическим ожиданием 0 и дисперсией 1. Какое из двух событий или имеет большую вероятность?

9.25. Случайная величина X имеет нормальное распределение с параметрами .Что больше: или

9.26. При измерении детали получаются случайные ошибки, подчиненные нормальному закону с мм. Найти вероятность того, что измерение будет произведено с ошибкой, не превосходящей 15 мм; не превосходящей 20 мм.

9.27. Автомат изготовляет подшипники, которые считаются годными, если отклонение Х от проектного размера по модулю не превосходит 0,77 мм. Каково наиболее вероятное число годных подшипников из 100, если Х - случайная вели-чина, распределенная нормально с  = 0,4мм?

9.28. Диаметр деталей, изготовленных цехом, является случайной величиной, распределенной по нормальному закону. Дисперсия ее равна 0,0001 cм²,а математическое ожидание 2,5 см. В каких границах можно практически гарантировать диаметр детали (за достоверное принимается событие, вероятность которого 0,9973)?

9.29. Рост взрослых женщин является случайной величиной, распределенной по нормальному закону. Математическое ожидание ее пусть равно 164 см, а среднее квадратическое отклонение 5,5 см. Найти плотность вероятности и функцию распределения этой случайной величины. Вычислить вероятность того, что ни одна из пяти наудачу выбранных женщин не будет иметь рост более 160 см.

9.30. Результаты измерения расстояния между двумя населенными пунктами подчинены нормальному закону с параметрами: математическое ожидание равно 16 км, а среднее квадратическое отклонение равно 100 м. Найти вероятность того, что расстояние между этими пунктами а) не меньше 15,8 км; б) не более 16,25 км.
Задача № 10.

10.1. По некоторой цели производятся два выстрела. Вероятность попадания при одном выстреле равна P. Рассматриваются две случайные величины: Х - число попаданий в цель, Y - число промахов. Составить таблицу распределения и определить числовые характеристики системы.

10.2. Случайная точка на плоскости распределена по закону, заданному таблицей:

Y X 0 1

-1 0,1 0,15

0 0,15 0,25

1 0,2 0,15
Найти числовые характеристики системы (X,Y).

10.3. Матрица распределения системы двух дискретных случайных величин(X,Y) задана таблицей: X Y 0 2 5

1 0,1 0 0,2

2 0 0,3 0

4 0,1 0,3 0

Найти числовые характеристики системы (Х,Y).

10.4. Изготовляемые в цехе втулки сортируются по отклонению их внутреннего диаметра от номинального размера на 4 группы со значениями 0,01; 0,02; 0,03 и 0,04 мм и по овальности на четыре группы 0,002; 0,004; 0,006;

0,008 мм. Совместное распределение диаметра (X) и овальности (Y) втулок задано таблицей (Табл.10.3):

Y Х 0,01 0,02 0,03 0,04

0,002 0,01 0,02 0,03 0,04

0,004 0,03 0,24 0,15 0,06

0,004 0,04 0,10 0,08 0,08

0,008 0,02 0,04 0,04 0,02

Найти числовые характеристики системы случайных величин .

10.5. Дана таблица, определяющая закон распределения системы двух cлучайных величин (X,Y):

Y

X 20 40 60

10 3 0

20 2 4 2

30 2 5

Найти : .

10.6. Система (X,Y) задана следующей двумерной таблицей распределения вероятностей:

X 0 1 2 3 4 5 6

Y

0 0,202 0,174 0,113 0,062 0,049 0,023 0,004

1 0 0,099 0,064 0,040 0,031 0,020 0,006

2 0 0 0,031 0,025 0,018 0,013 0,008

3 0 0 0 0,001 0,002 0,004 0,011

Найти вероятность и корреляционную матрицу.

10.7. Однотипные детали в зависимости от точности изготовления различаются по форме на круглые и овальные, а по весу - на легкие и тяжелые. Вероятности того, что взятая наудачу деталь окажется круглой и легкой, овальной и легкой, круглой и тяжелой, овальной и тяжелой, соответственно равны . Взята одна деталь. Найти математические ожидания и дисперсии числа круглых деталей X и числа легких деталей Y, а также корреляционный момент k_xy между числом круглых и числом легких деталей, если = 0,40, = 0,05, = 0,10.

8. 
   Производится два выстрела по мишени в неизменных условиях. Вероятность попадания в мишень при одном выстреле равна P. Случайные величины: X - число выстрелов до первого попадания (включительно), Y - число промахов. Необходимо: а) описать закон распределения случайного вектора (X,Y) и законы распределения каждой компоненты; б) вычислить вероятность P(X = Y);
   

в) вычислить коэффициент корреляции r_xy.; г) определить зависимы или неза-висимы компоненты X, Y.

10.9. Бросаются две одинаковые игральные кости. Случайные величины:

X - индикатор четности суммы выпавших очков (т.е. X = 1, если эта сумма четная, и X = 0 в противном случае), Y - индикатор четности произведения выпавших очков (т.е. Y = 1, если это произведение четно и Y = 0 в противном случае).

а) Описать закон распределения случайного вектора (X, Y).

б) Вычислить функцию распределения F(X, Y).

в) Вычислить корреляционный момент.

10. 
    Число X выбирается случайным образом из множества целых чисел
    

. Затем из того же множества выбирается наудачу число Y, больше первого или равное ему.

а) Описать закон распределения случайного вектора (X,Y).

б) Определить, зависимы или независимы случайные компоненты X и Y.

в) Построить условный закон распределения компоненты X при условии, что Y приняло значение, равное 2.

г) Вычислить основные характеристики

10.11. Случайный вектор (X,Y) имеет следующее распределение вероятностей:



_Y ^X 0 1

-1 0,1 0,2

0 0,2 0,2

1 0,1 0,2

Найти математическое ожидание и дисперсию величины

10.12. В продукции завода брак вследствие дефекта A составляет 3 %, а вследствие дефекта B - 4,5 %. Годная продукция составляет 95 %. Найти коэффициент корреляции дефектов A и B . Указание. Ввести в рассмотрение случайную величину X = 1, если данное изделие обладает дефектом A и X = 0 в противном случае. Аналогично Y = 1; 0 в зависимости от того, обладает или нет это изделие дефектом B.

10.13. Два стрелка, независимо друг от друга, делают по два одиночных (независимых) выстрела каждый по своей мишени. Случайная величина X - число попаданий первого стрелка, Y - число попаданий второго стрелка. Вероятность попадания при одном выстреле для первого стрелка P₁ = 0,7; для второго P₂ = 0,4. Построить матрицу распределения вероятностей системы случайных величин (X,Y).

10.14. Два стрелка независимо друг от друга делают по одному выстрелу каждый по своей мишени. Случайная величина X - число попаданий первого стрелка. Y - число попаданий второго стрелка. Вероятность попадания при одном выстреле для первого стрелка P₁ = 0,7, для второго P₂ = 0,4. Построить матрицу распределения вероятностей системы случайных величин (u,v), где

.

10.15. Система случайных величин (Х,Y) имеет следующее распределение вероятностей:

Y X 0 1

-1 0,1 0,2

0 0,2 0,3

1 0 0,2

Найти математическое ожидание и дисперсию случайной величины .

10.16. Имеется система случайных величин (X,Y), где

и коэффициент корреляции . Найти математическое ожидание и дисперсию случайной величины

10.17. Случайные величины X и Y связаны соотношением , где - неслучайные величины . Найти: а) Коэффициент корре-ляции ; б) Отношение среднеквадратических отклонений .

10.18. Дважды бросается игральная кость. Случайные величины: X - число появлений шестерки, Y - число появлений нечетной цифры. Описать закон распре-деления случайного вектора (X, Y). Установить зависимы или независимы компоненты Х и Y.

10.19.Дважды бросается игральная кость. Случайные величины: X - число появлений единицы, Y - число появлений нечетной цифры. Описать закон распре-деления случайного вектора (X,Y). Вычислить основные характеристики случайного вектора: .

10.20. Дважды бросается игральная кость. Случайные величины: X - число появлений шестерки, Y - число появлений четной цифры. Описать закон распределения случайного вектора (X, Y). Описать условный закон распределения случайной величины X при условии Y = 2 и при этом условии вычислить условное математическое ожидание .

10.21. Совместное распределение (X,Y) задано формулами:





Найти одномерные распределения X,Y и распределения .

10.22. Совместное распределение задано формулами:

,



Найти совместное распределение случайных величин:

10.23. Совместное распределение (X,Y) задано формулами





Найти

10.24. Совместное распределение случайных величин определяется формулами



Найти Являются ли X,Y независимыми величинами?

10.25. Случайные величины независимы; Найти:

а) коэффициент корреляции величин Х₁+Х₂, Х₃+Х₄+Х₅; б) коэффициент корреляции величин Х₁+Х₂+Х₃, X₃+X₄+X₅ .

10.26.Дана таблица, определяющая закон распределения системы двух случайных величин (Х,Y):



X Y 2 4 6

1  3 0

2 4 2 2

3 5 2 

Найти: а). , б). в). г) .

10.27. Система случайных величин (Х,Y) распределена по закону, выраженному таблицей:

Y X 0 1

-1 0,1 0,15

0 0,15 0,25

1 0,2 0,15
Описать условный закон распределения случайной величины Х, при условии Y = 0, при этом же условии вычислить условное математическое ожидание .

10.28. В таблице приведены данные о возможных сочетаниях отклонений длины валика (Х) и диаметра (Y) от номинальных размеров и соответствующие вероятности:

X Y	-1	0	1
-2	0,15	0,35	0,05
3	0,10	0,25	0,10

Найти закон распределения случайной величины Z = X + Y и проверить справед-ливость формулы

10.29. Случайные величины независимы. По заданным законам распреде-ления случайных величин найти закон распределения системы случайных величин

X 1 2 3 Y 4 6 8 10

P 0,3 0,5 0,2 P 0,1 0,4 0,3 0,2

10.30. Дважды бросается игральная кость. Случайные величины: Х - число появлений шестерки, Y - число появлений нечетной цифры. Вычислить вероятности .
Задача № 11.

11.1. Система случайных величин имеет равномерное распределение внутри квадрата со стороной a. Диагонали квадрата совпадают с осями координат. Определить: а) плотность совместного распределения вероятностей системы (X,Y);

б) плотность распределения вероятностей каждой из случайных величин, входящих в систему.

11.2. Система трех случайных величин (X, Y, Z) распределена равномерно внутри цилиндра, ось которого совпадает с осью OZ и точкой O делится пополам. Радиус цилиндра равен R, а высота 2h. Определить: а) плотность совместного распределения вероятностей системы (X, Y, Z); б) плотность распределения каждой из случайных величин, входящих в систему.

11.3. Система случайных величин (X, Y) подчинена закону распределения с плотностью распределения вероятностей , если и если . Найти: 1) a ; 2); 3)дисперсии ;

4) коэффициент корреляции .

11.4. Система двух случайных величин (X,Y) подчинена нормальному закону распределения. Рассеивание круговое. Найти вероятность попадания случайной точки (X, Y) в круг, центр которого cовпадает с центром рассеивания, а радиус равен двум вероятным отклонениям (Вероятное отклонение где

= 0,476936).

11.5. Плотность совместного распределения вероятностей системы случайных величин X,Y имеет вид: , где Определить параметры распределения. Выяснить, зависимы или независимы случайные величины X, Y.

11.6. Плотность совместного распределения системы случайных величин X, Y:

. Найти коэффициент A. Найти законы распределения случайных величин X, Y. Установить, зависимы или нет случайные величины X, Y.
11.7. Система двух случайных величин (X, Y) подчинена закону распределения с плотностью совместного распределения: . Определить коэффициент A и найти радиус круга с центром в начале координат, вероятность попадания в который равна P.

11.8. Система случайных величин (X,Y) имеет плотность совместного распределения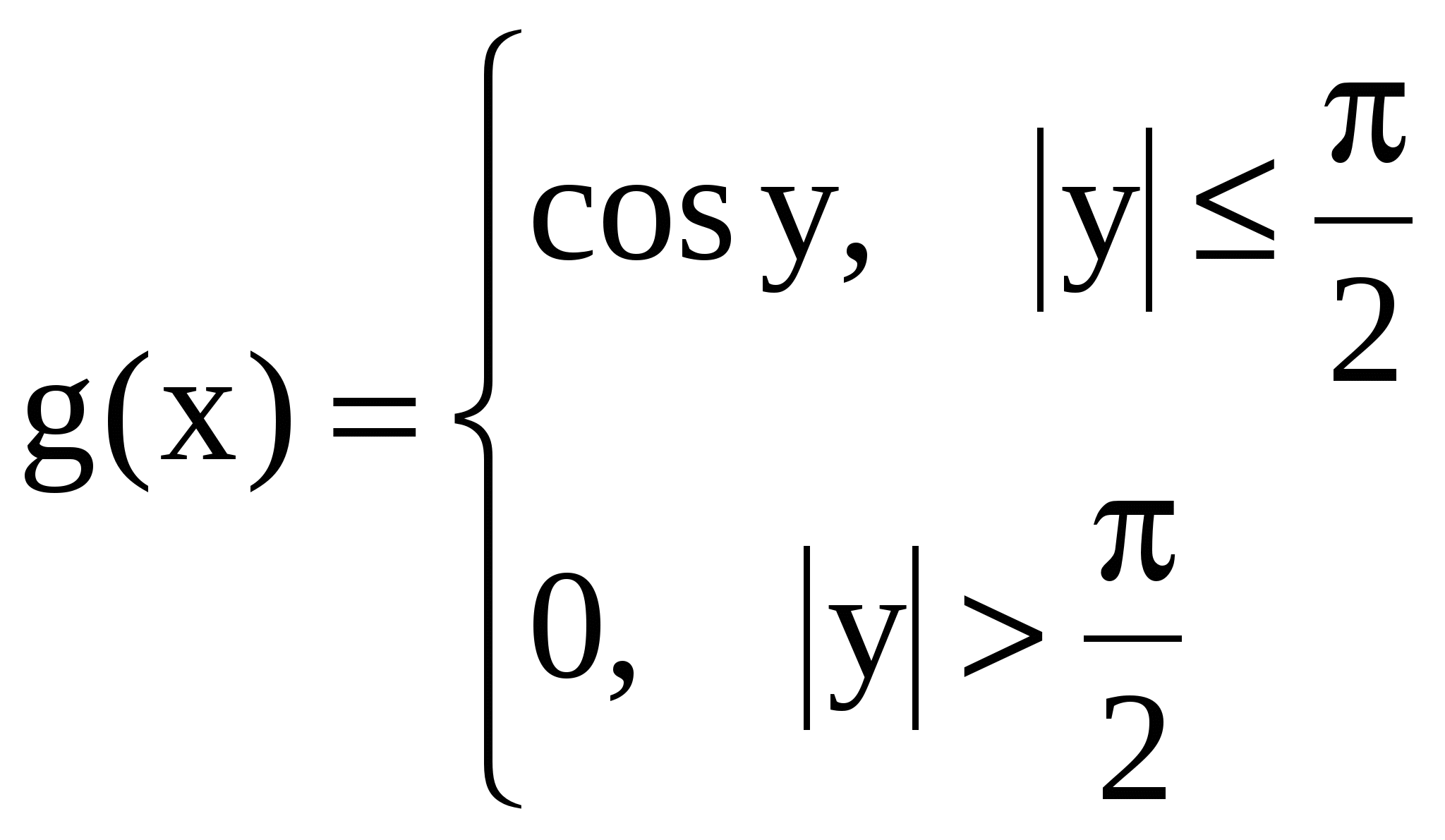

, где . Найти a. Написать выражение плотностей распределения случайных величин X и Y. Определить математические ожидания и дисперсии случайных величин X и Y.

11.9. Производится единичное бомбометание по прямоугольной наземной цели. Ширина цели равна 20 м, а длина 100 м. Прицеливание по центру цели. Оси рассеивания совпадают с направлением полета и с перпендикуляром к этому направлению. Вероятное отклонение в направлении полета равно 60 м, в направлении, перпендикулярном полету – 40 м. Систематические ошибки отсут-ствуют. Вероятность попадания в цель при сбрасывании одной бомбы. Указание: Вероятное отклонение

11.10. Плотность совместного распределения системы случайных величин X, Y равна . Определить A. Найти функции распределения и плотности распределения случайных величин, входящих в систему. Определить, зависимы или независимы случайные величины: X, Y.

11.11. Дана плотность совместного распределения случайных величин X, Y:

Определить вероятность попадания в прямоугольник:

y

(2;1,5)

0

(0;-1) (2;-1) х

11.12. Система случайных величин (X, Y) распределена с постоянной плот-ностью внутри квадрата. Найти плотности распределения случайных величин X, Y входящих в систему: