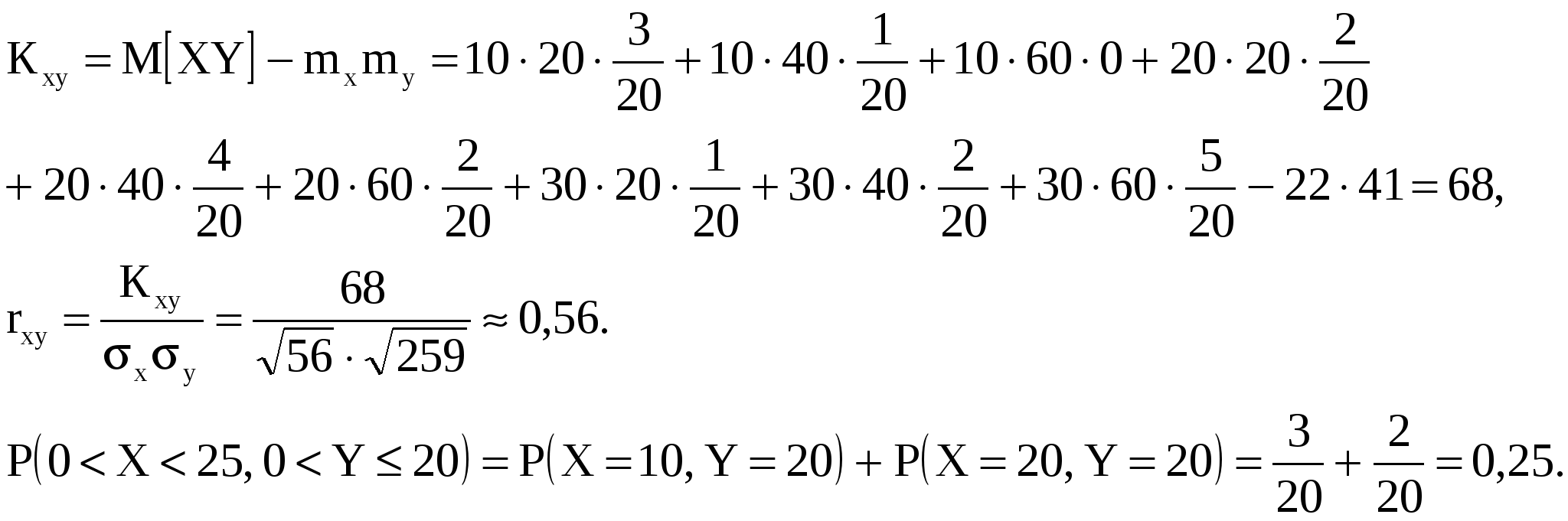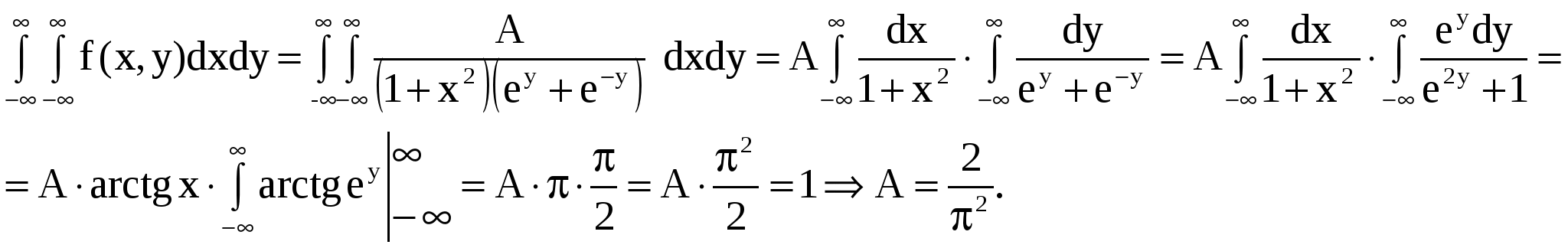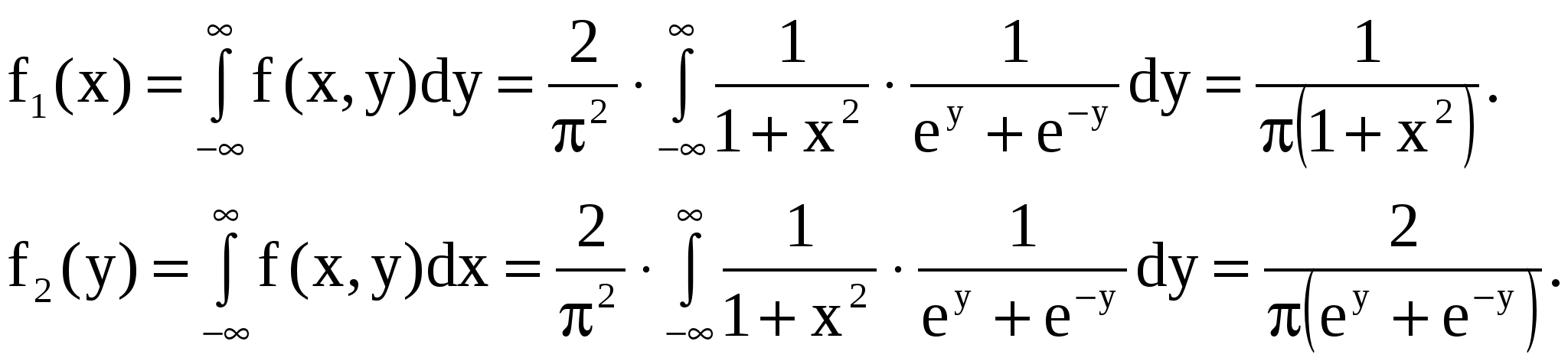|
|
Теория вероятностей. Задача 1 Пусть а в. Упростить выражения а в, АВ, а в с, АВС
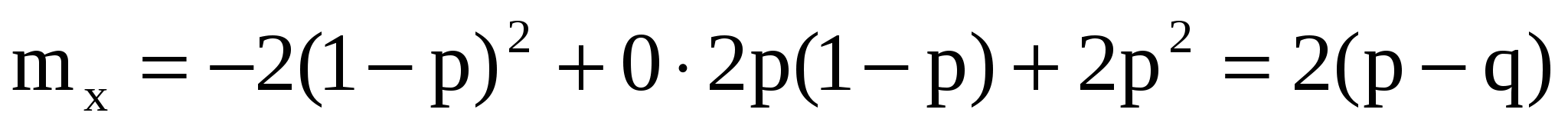 , ,
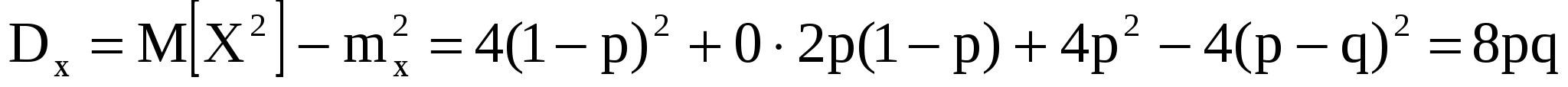 . .
 Случайная величина Случайная величина 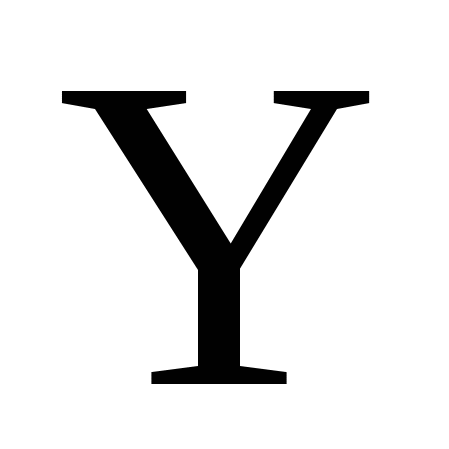 может принимать только одно значение: два с вероятностью, равной единице может принимать только одно значение: два с вероятностью, равной единице 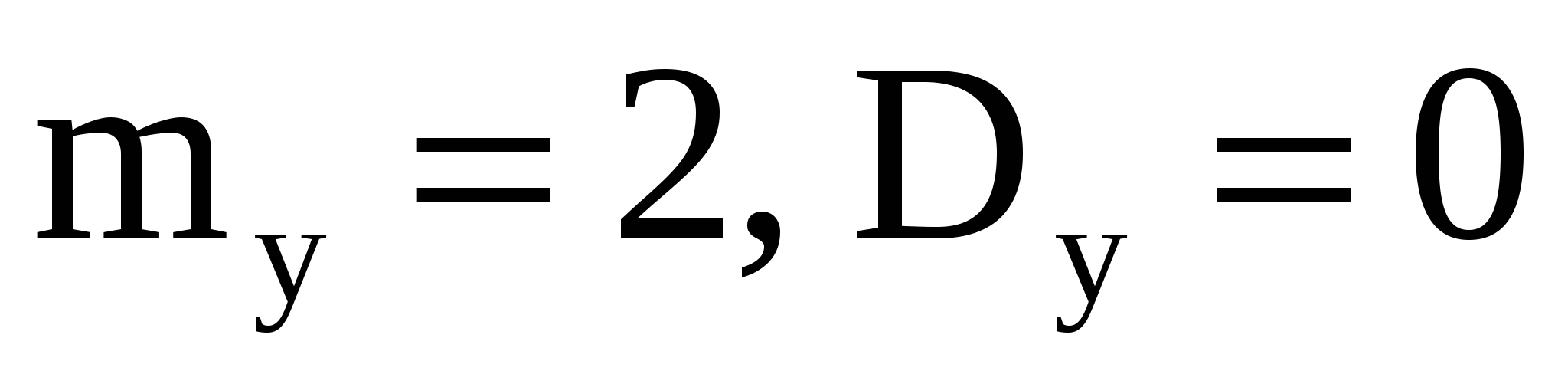 . .
 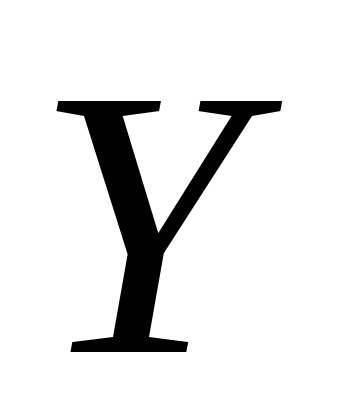 2 2
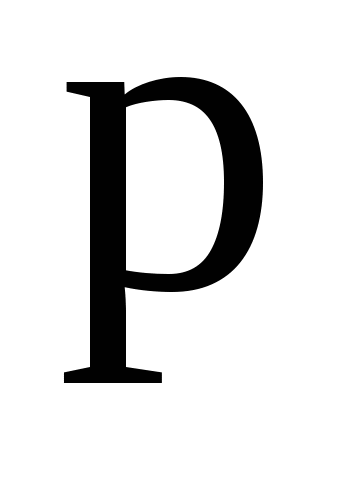 1 1
Задача 7. Дана функция 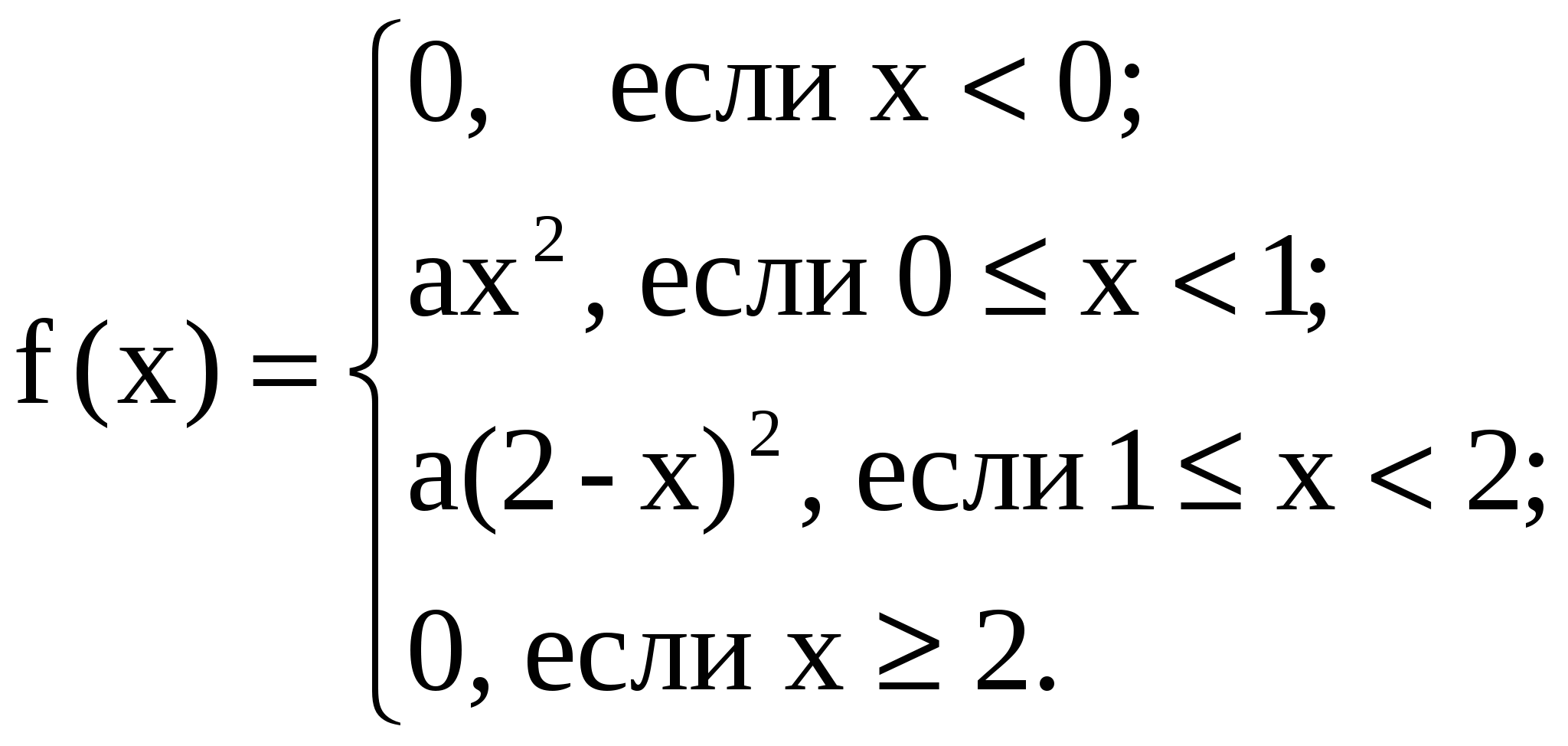
При каком значении  функция функция 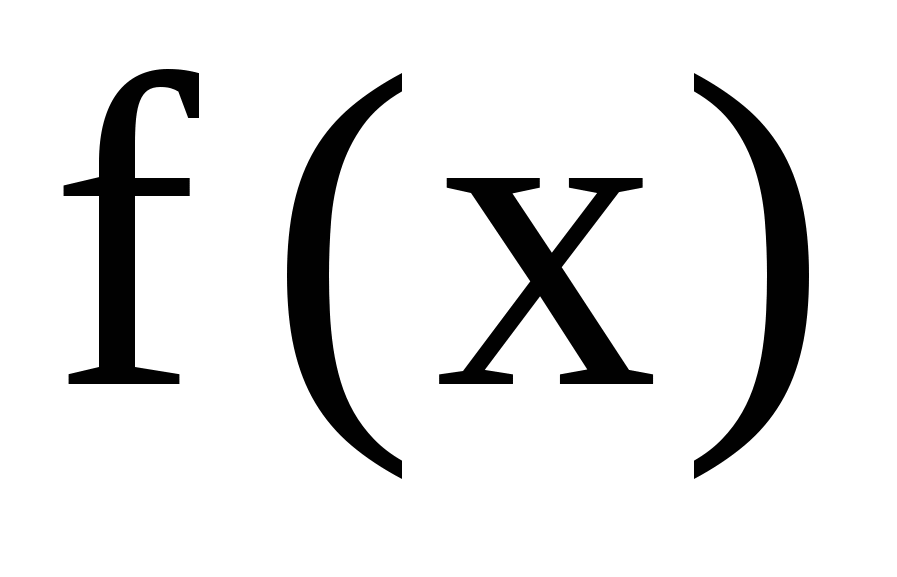 является плотностью распределения случайной величины является плотностью распределения случайной величины 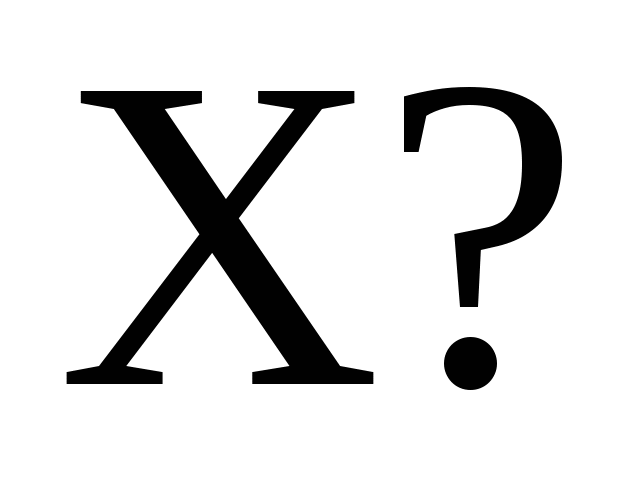 Найти функцию распределения случайной величины Найти функцию распределения случайной величины 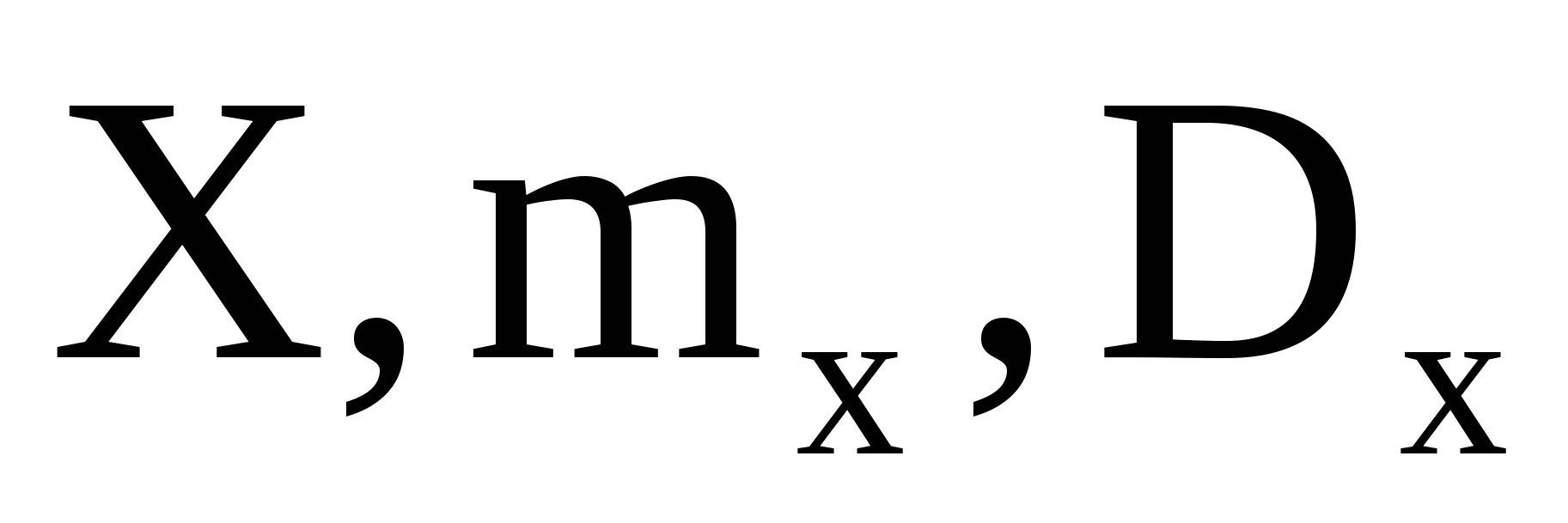 . .
Решение. Из основного свойства плотности следует
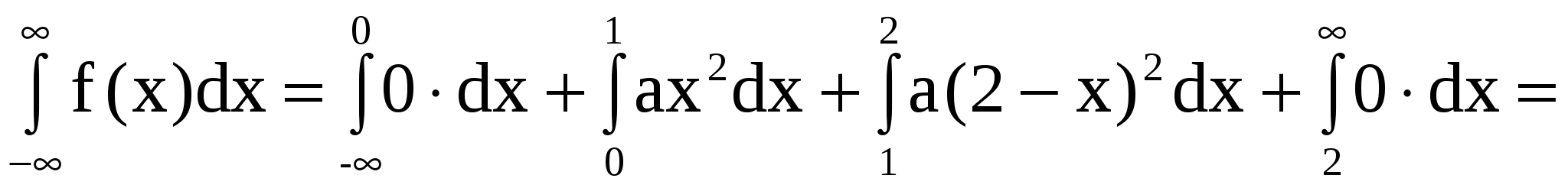
 . .
Для 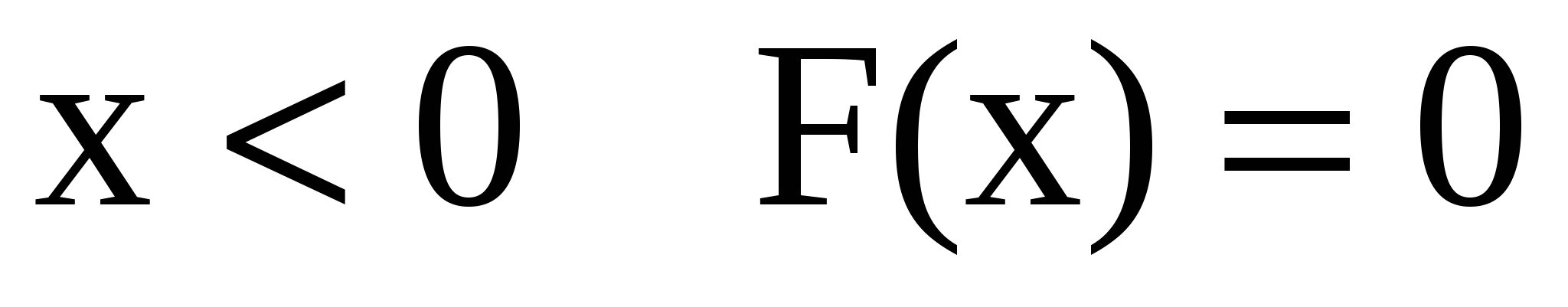 . .
Для 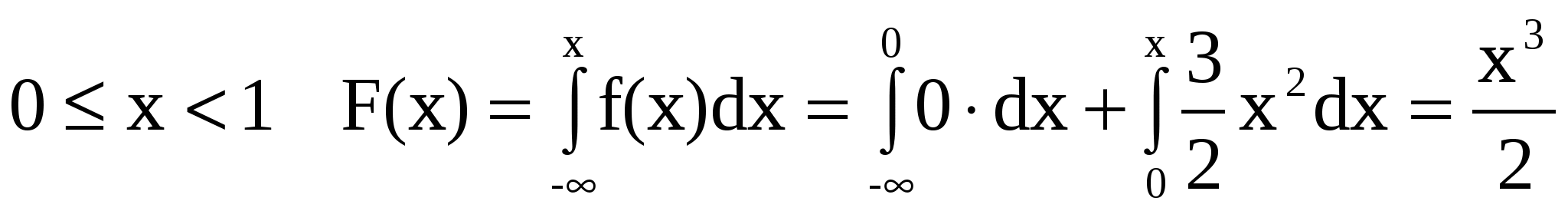 . .
Для 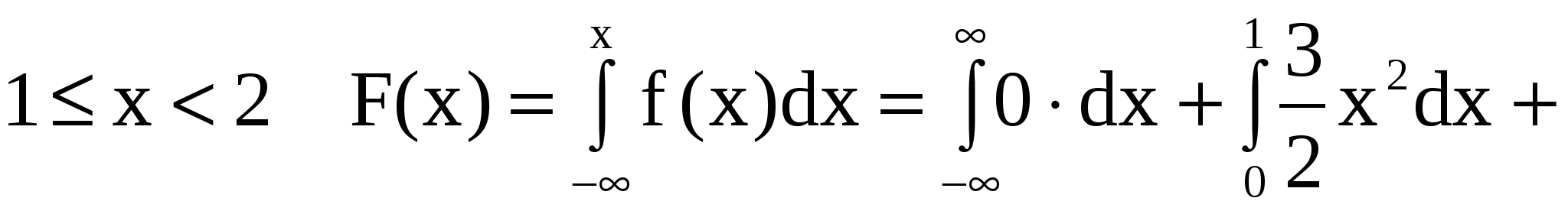
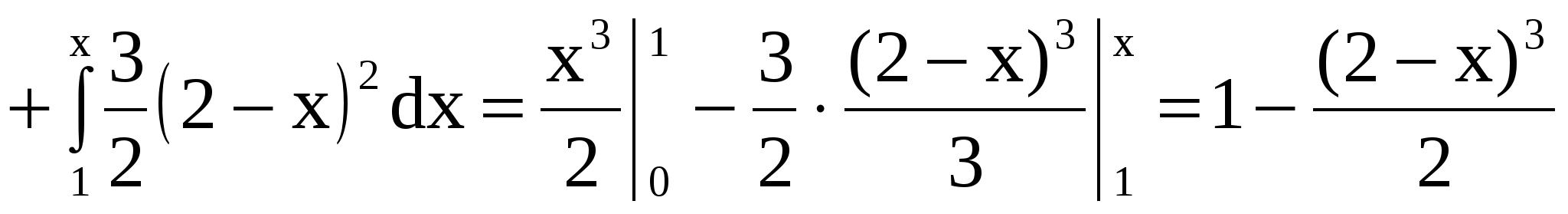 . .
Для 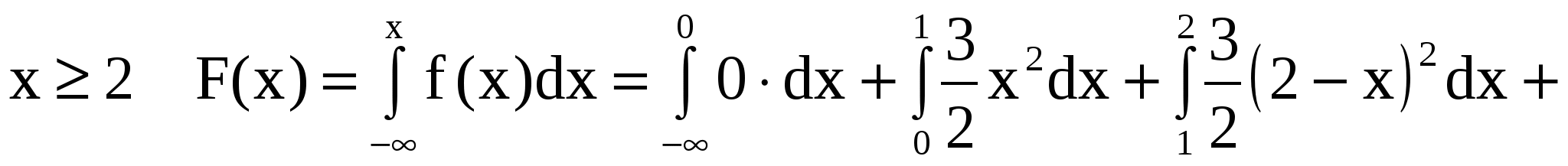
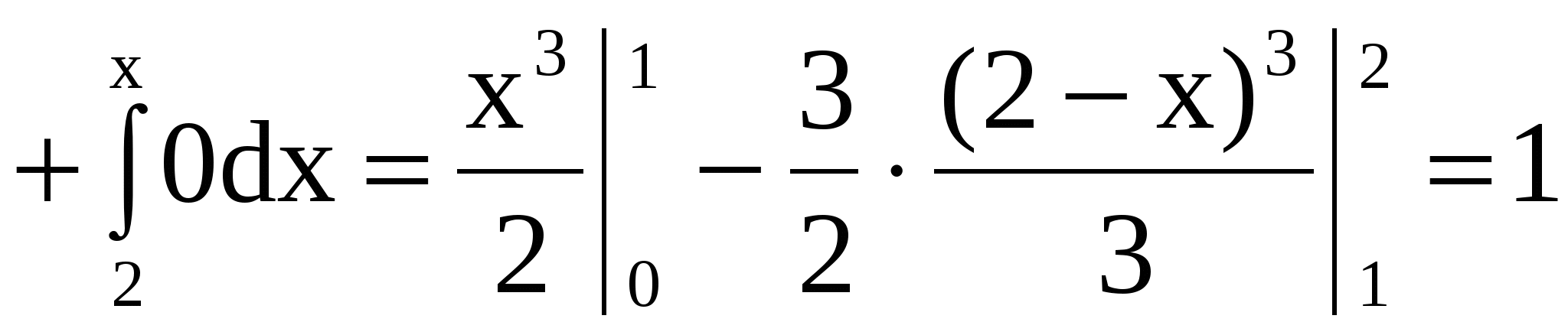 . .
Таким образом, 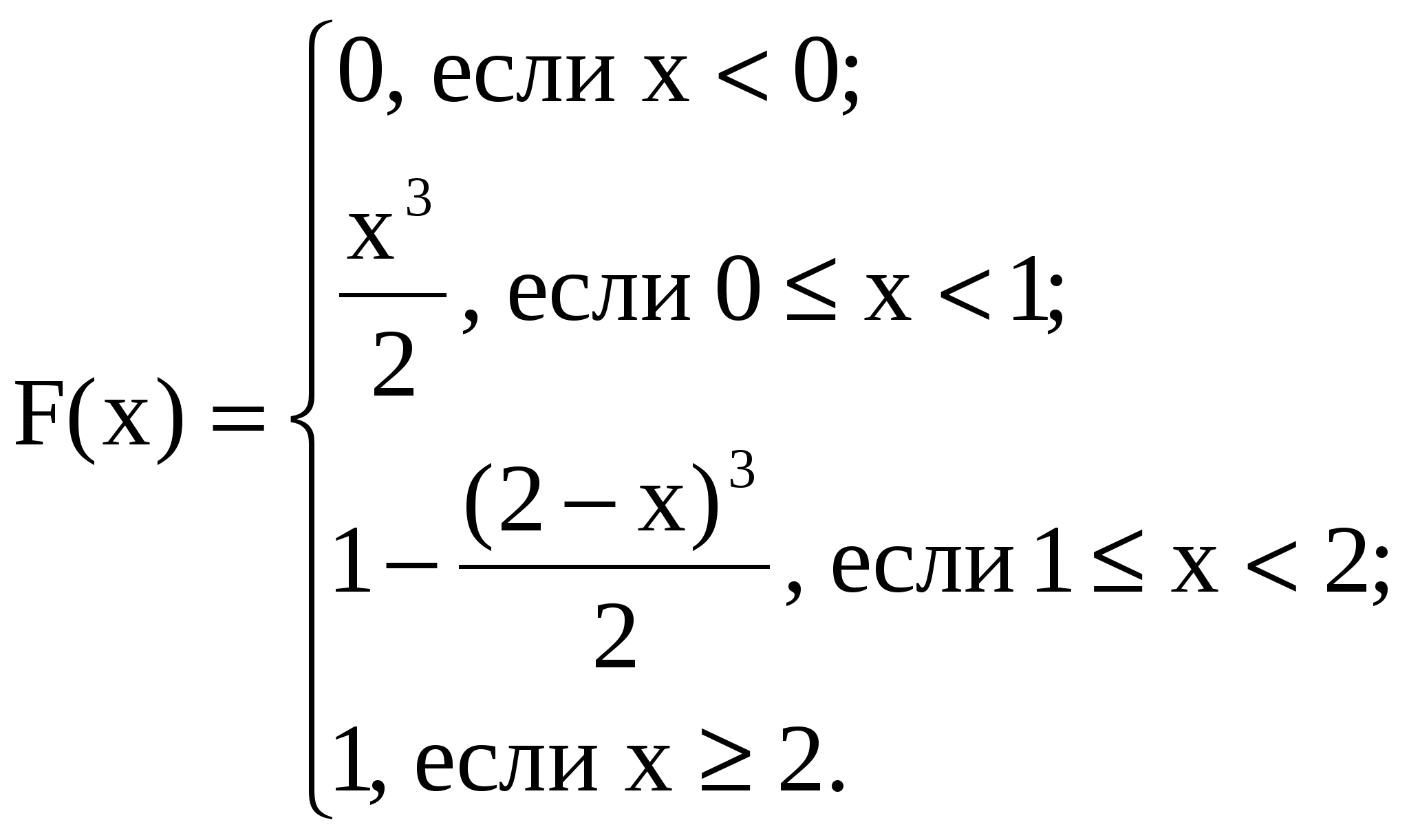
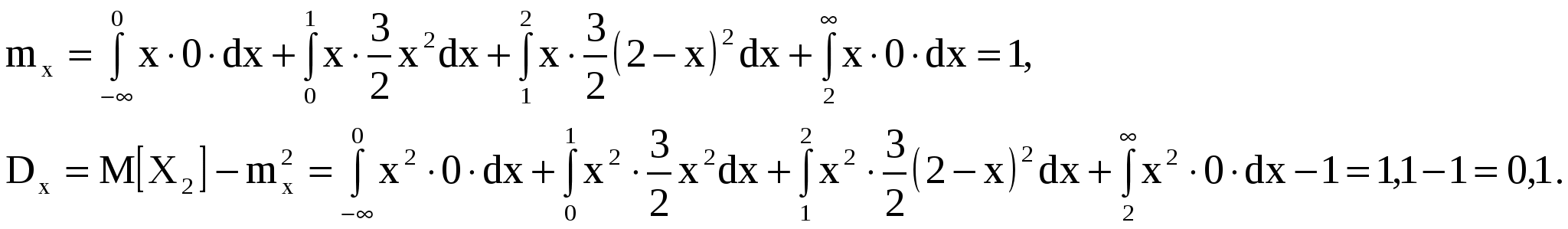
Задача 8. Время Tмежду двумя сбоями ЭВМ распределено по показательному закону с параметром 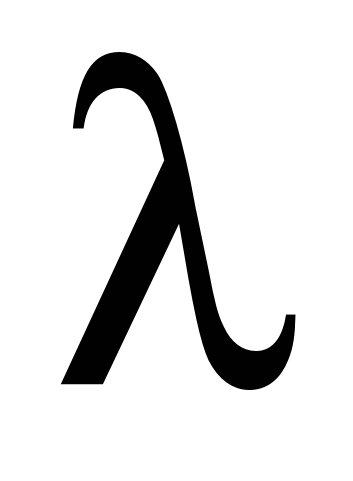 : : 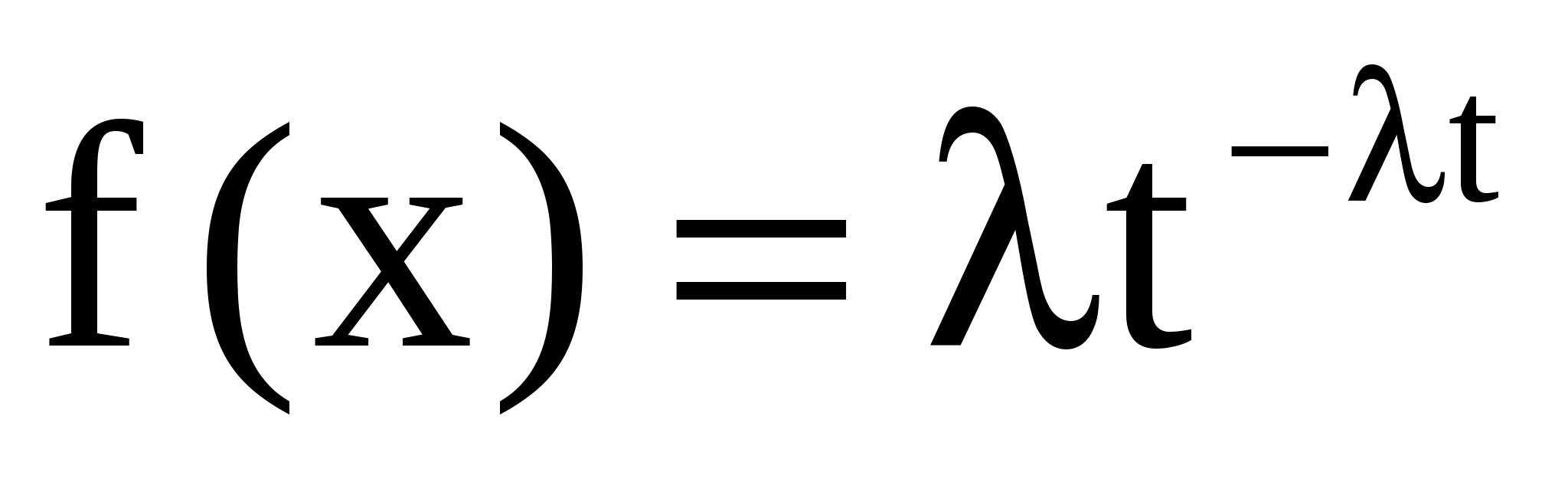 при при 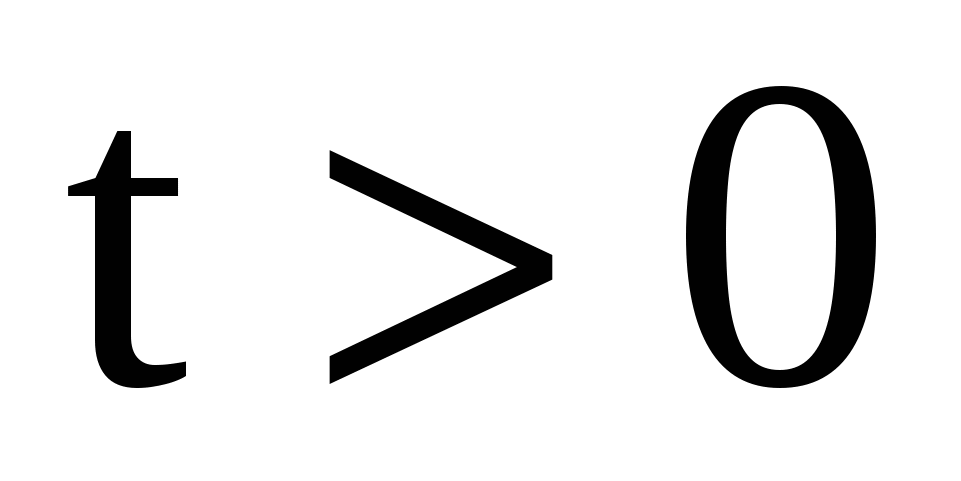 . Решение определенной задачи требует безотказной работы машины в течение времени . Решение определенной задачи требует безотказной работы машины в течение времени  . Если за время . Если за время  произошел сбой, то задачу приходится решать заново. Сбой обнаруживается только через время произошел сбой, то задачу приходится решать заново. Сбой обнаруживается только через время  после начала решения задачи. Рассматривается случайная величина после начала решения задачи. Рассматривается случайная величина 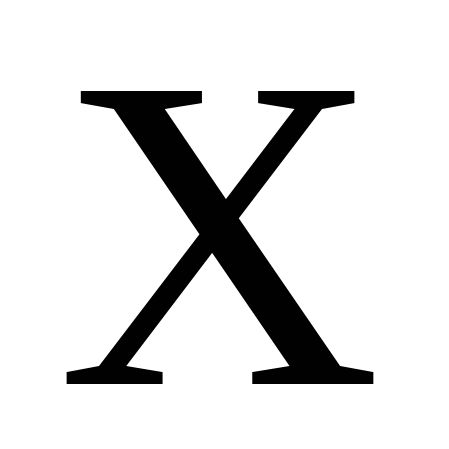 - время, за которое задача будет решена. Найти ее закон распределения и математическое ожидание (среднее время решения задачи). - время, за которое задача будет решена. Найти ее закон распределения и математическое ожидание (среднее время решения задачи).
Решение. Случайная величина 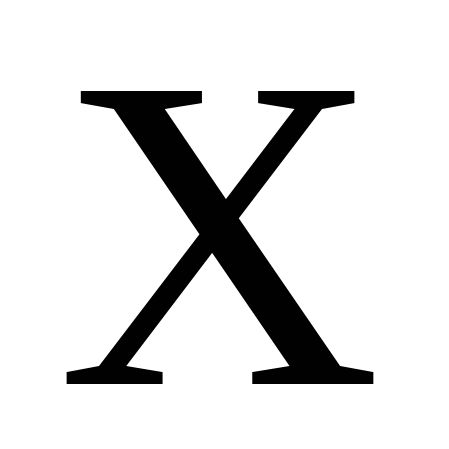 может принимать следующие значения: может принимать следующие значения:  ( за время ( за время  не произошло сбоя), 2 не произошло сбоя), 2 (на первом промежутке (на первом промежутке  сбой произошел, на втором промежутке сбой произошел, на втором промежутке  сбоя не было), 3 сбоя не было), 3 (на первых двух промежутках длины (на первых двух промежутках длины  сбои происходили, на третьем сбоя не было) и т. д. сбои происходили, на третьем сбоя не было) и т. д.
 . .
Обозначим 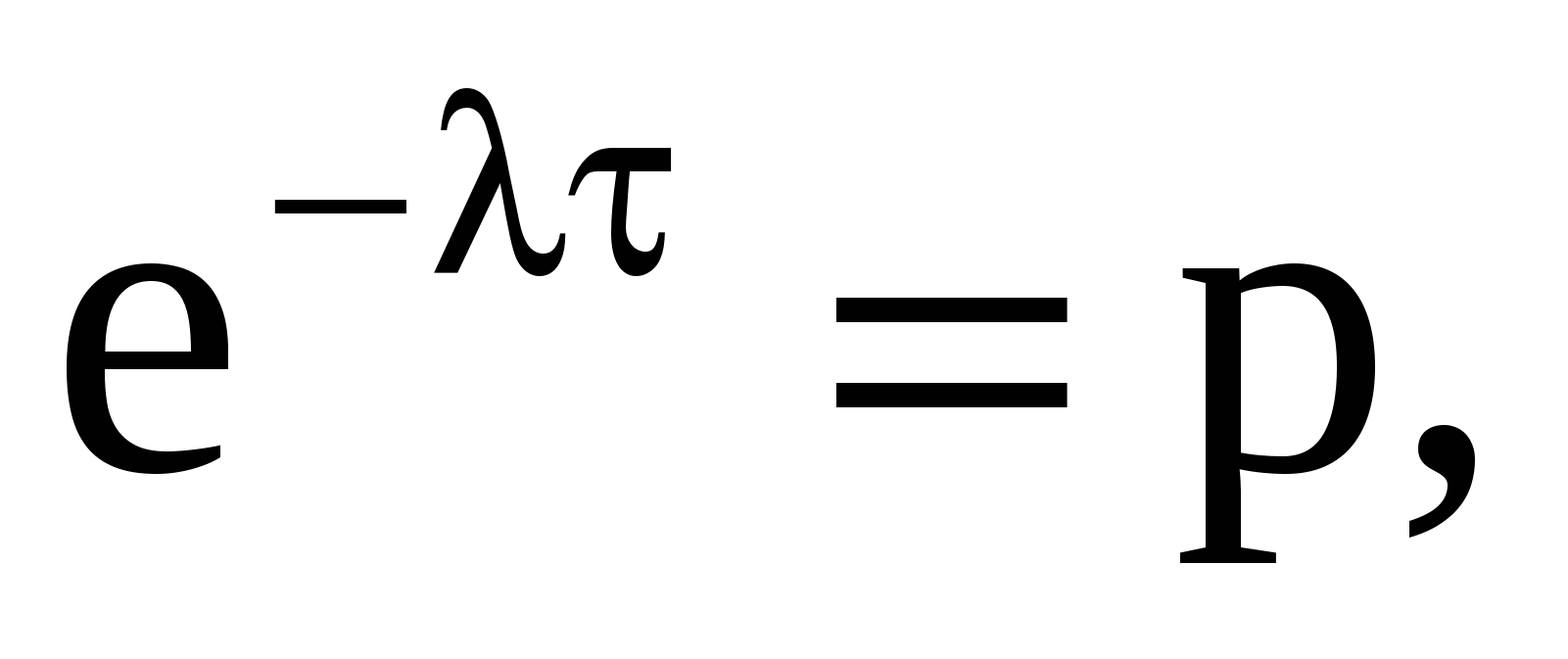 тогда тогда  - вероятность того, что за время - вероятность того, что за время  сбой произошел; сбой произошел; 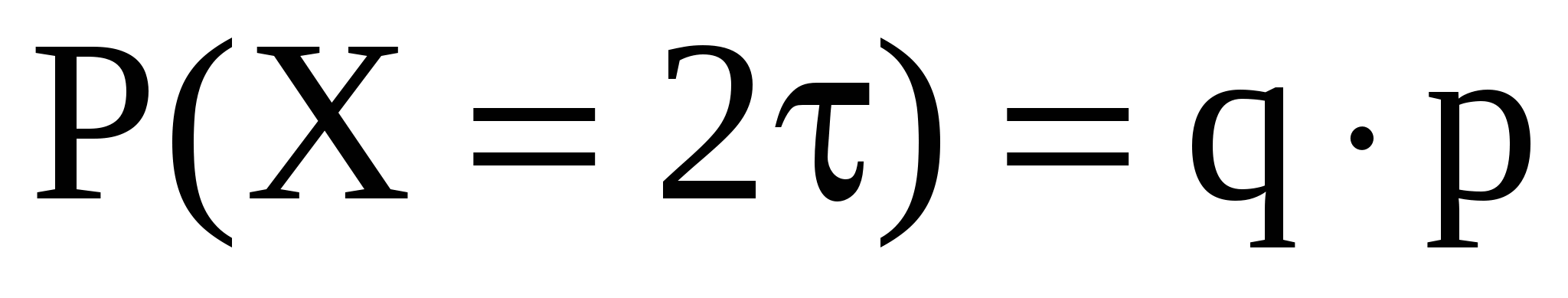 , , 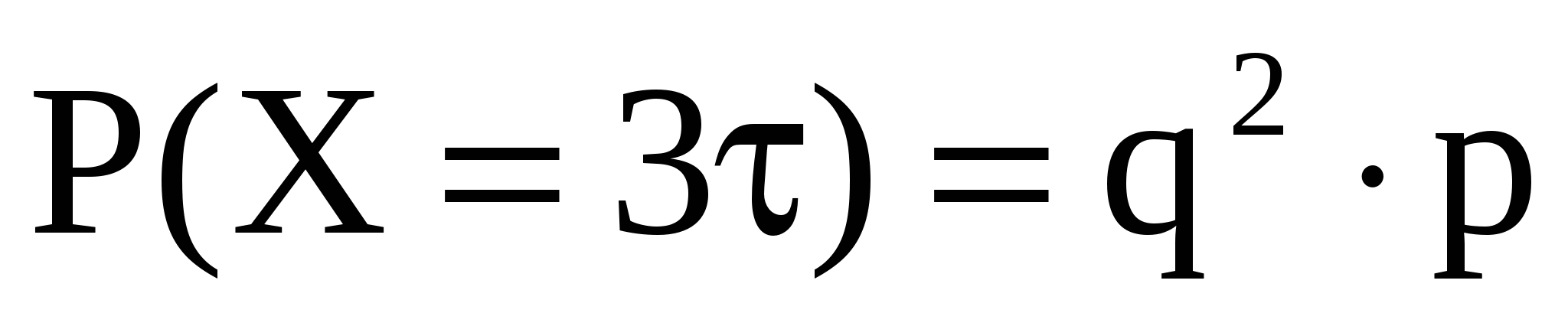 и т. д. и т. д.
    Ряд распределения случайной величины Ряд распределения случайной величины 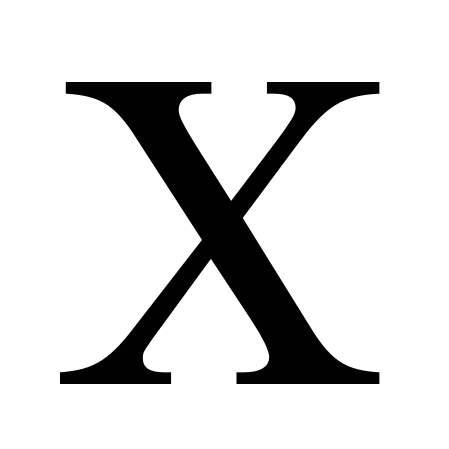
  Х Х  2 2 ... ... 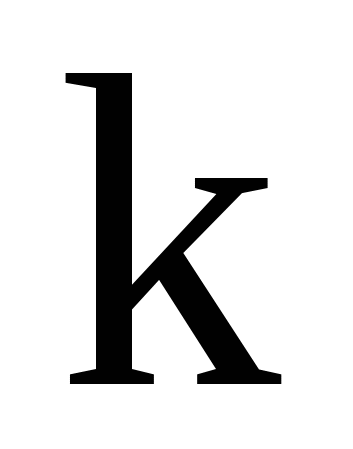  ... ...
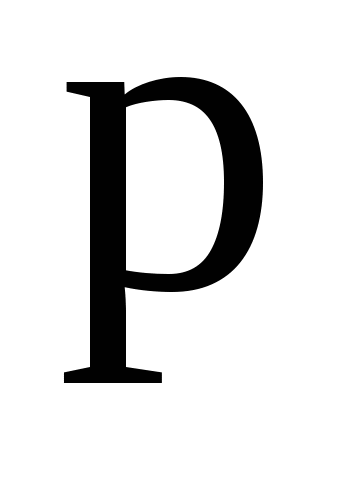 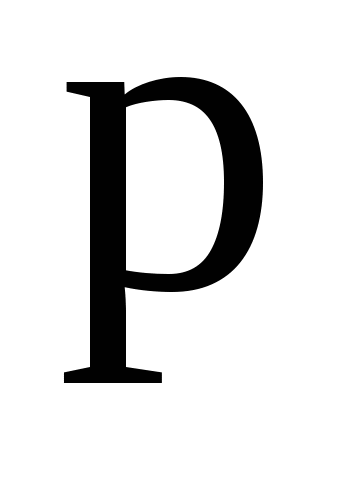 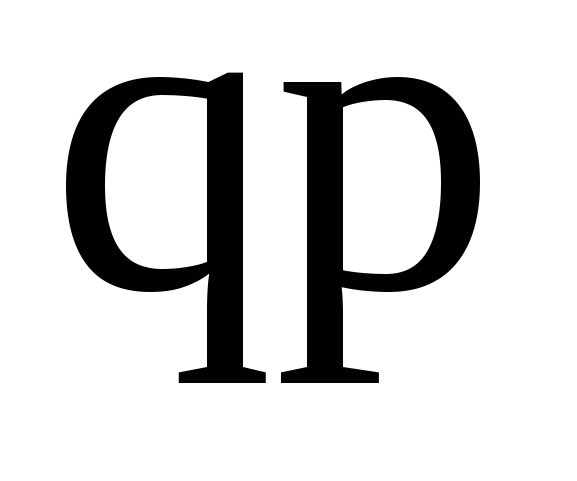 ... ... 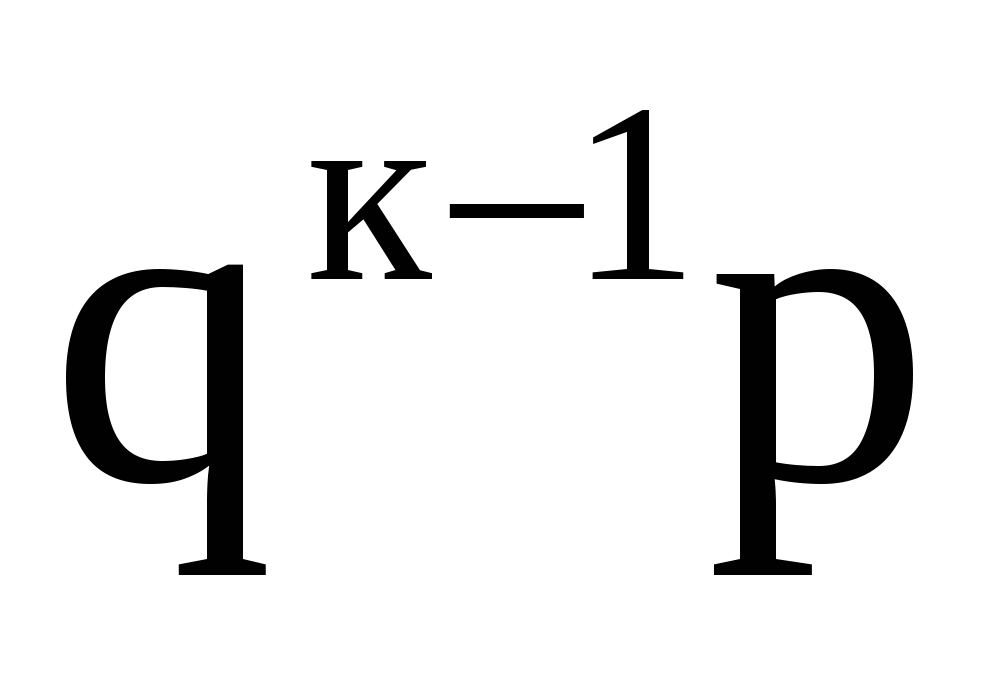 ... ...
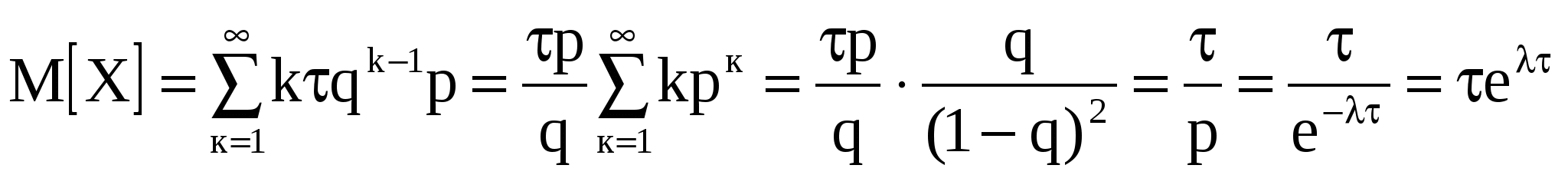 (вычисление суммы ряда (вычисление суммы ряда 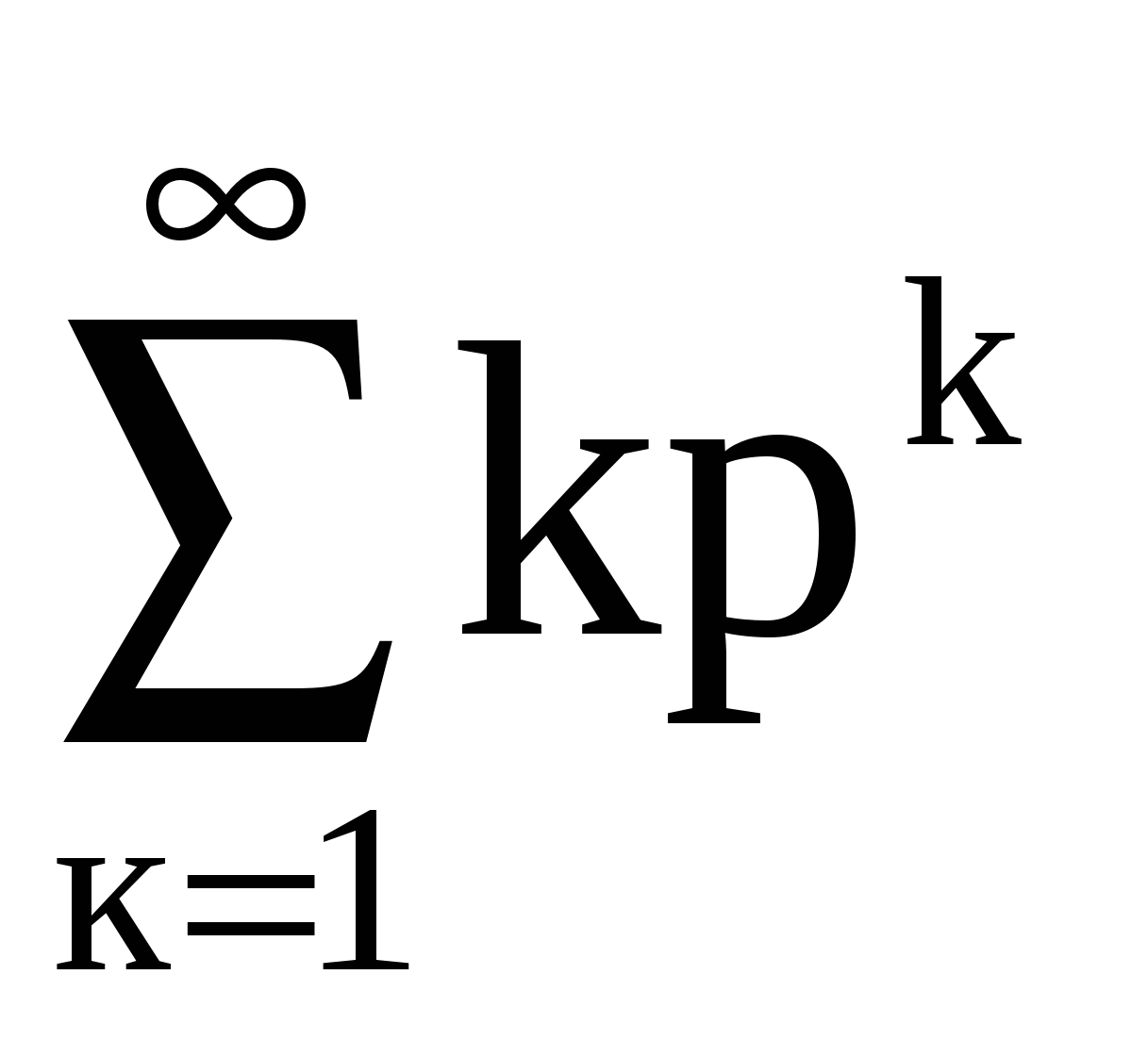 смотри методические указания к проведению практических занятий по теории вероятностей, часть 2, стр. 15). смотри методические указания к проведению практических занятий по теории вероятностей, часть 2, стр. 15).
Задача 9. Известно, что детали, выпускаемые по размерам диаметра, распре-деляются по нормальному закону. Параметры этого закона 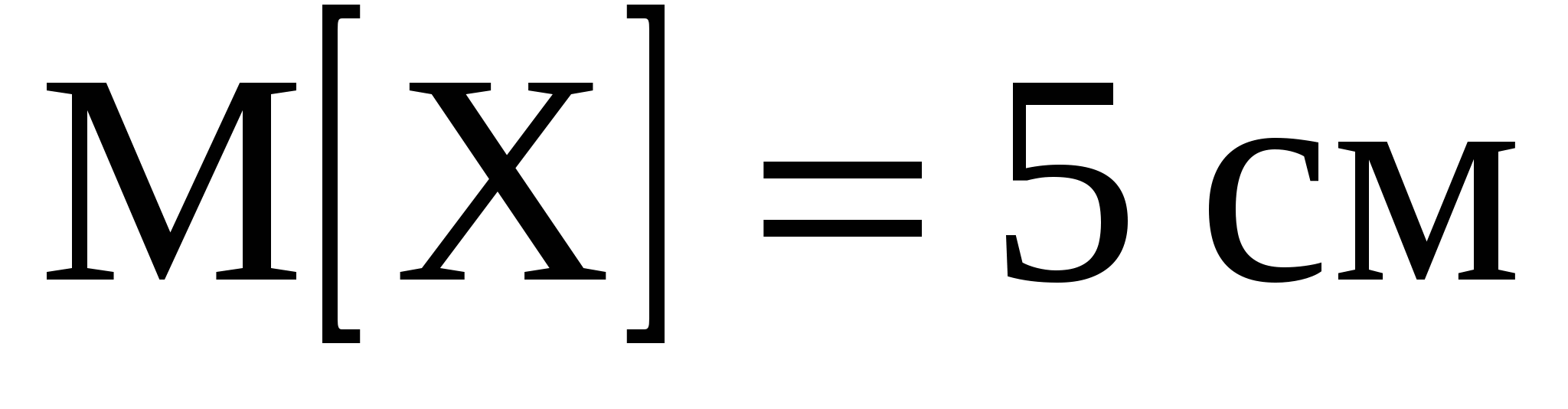 , , 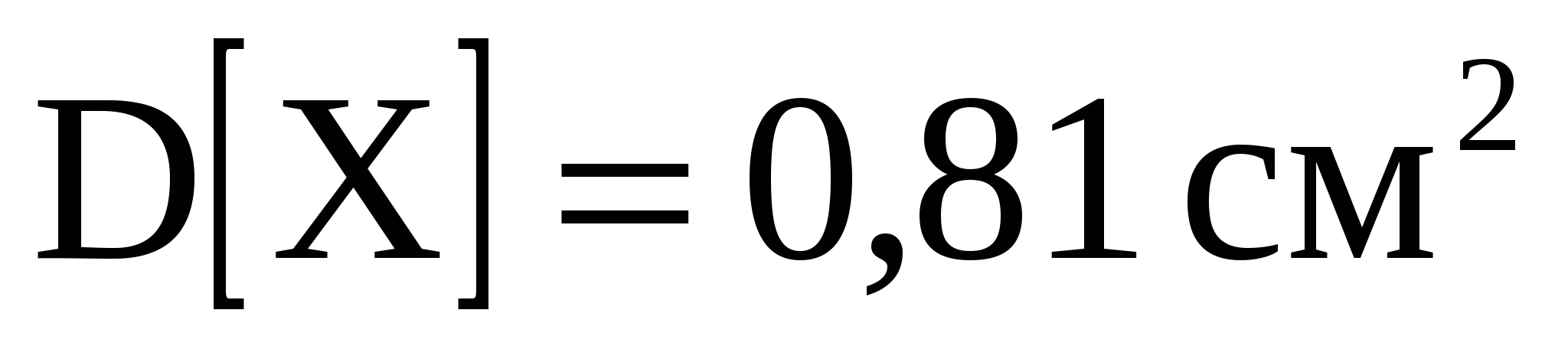 . Найти вероятность того, что диаметр наудачу взятой детали имеет размеры в пределах от 4 до 7 см. . Найти вероятность того, что диаметр наудачу взятой детали имеет размеры в пределах от 4 до 7 см.
Решение. 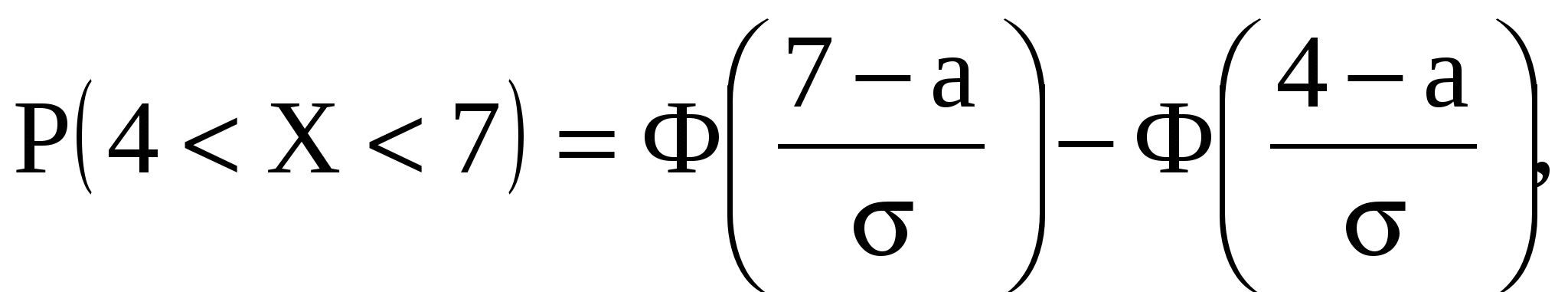 где где  - математическое ожидание, - математическое ожидание,  - среднее квадратическое отклонение. Таким образом, - среднее квадратическое отклонение. Таким образом, 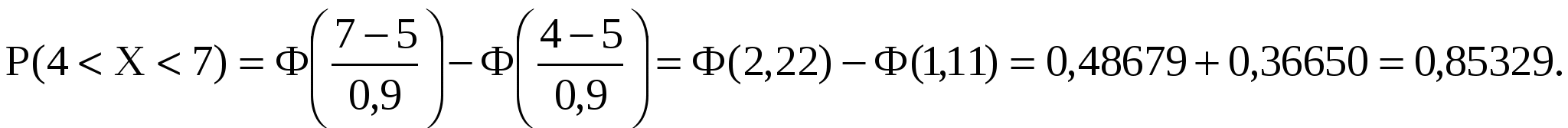
Х/Y 20 40 60
10  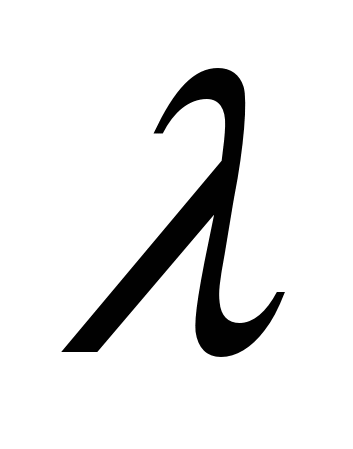 0 0
20 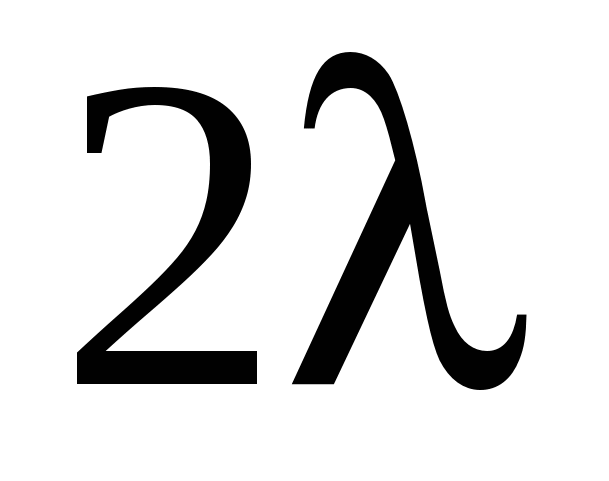  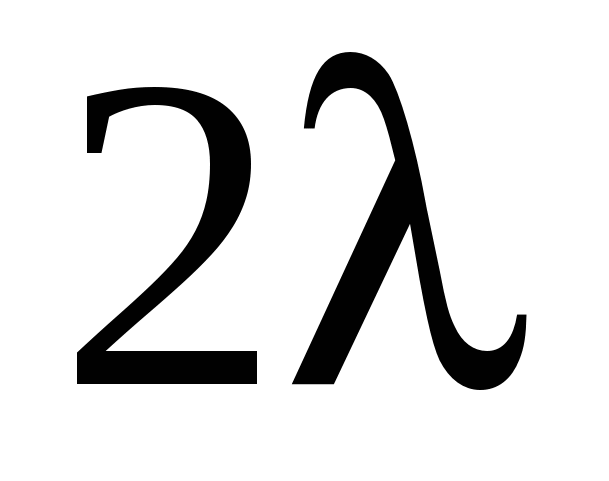
30 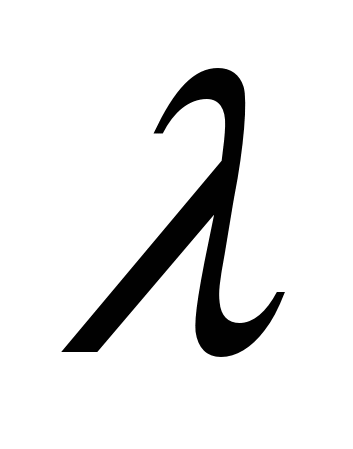 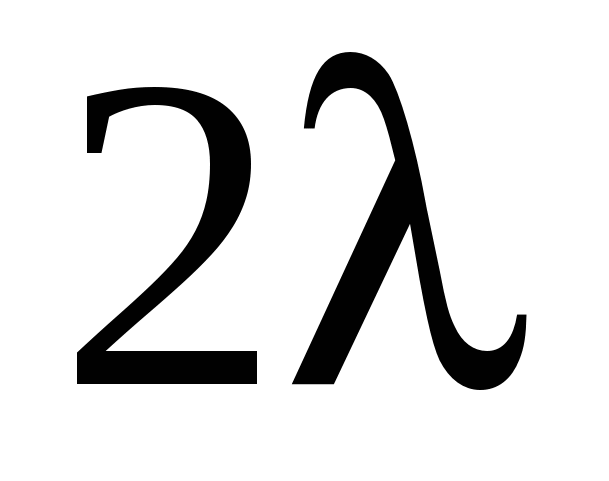 
   Задача 10. Закон распределения системы дискретных случайных величин Задача 10. Закон распределения системы дискретных случайных величин 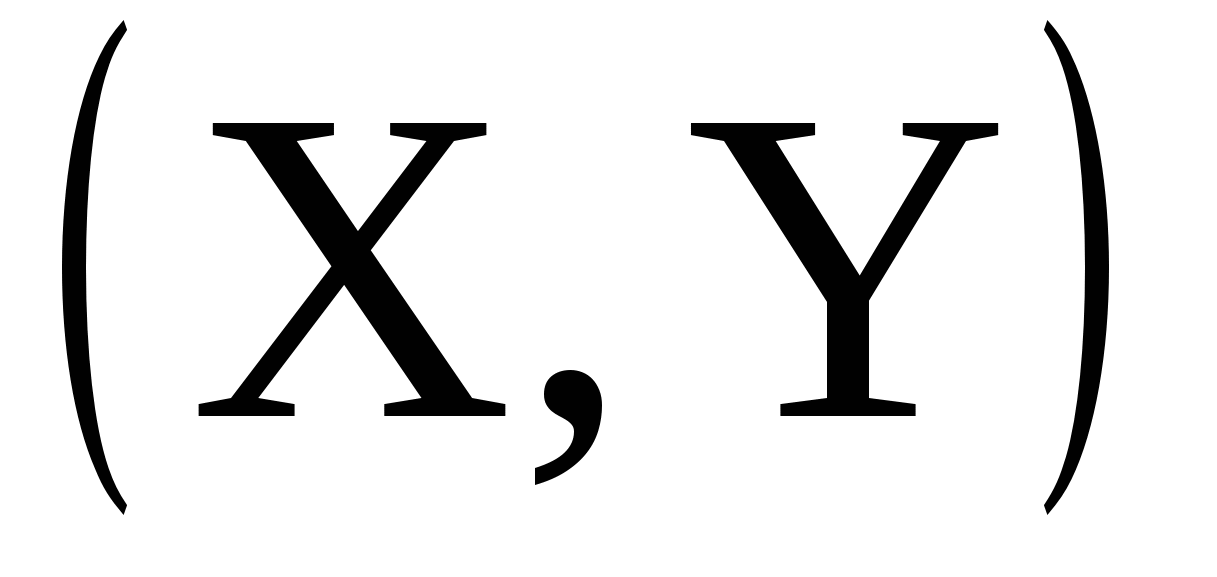
 задан таблицей: задан таблицей:


Найти: а) 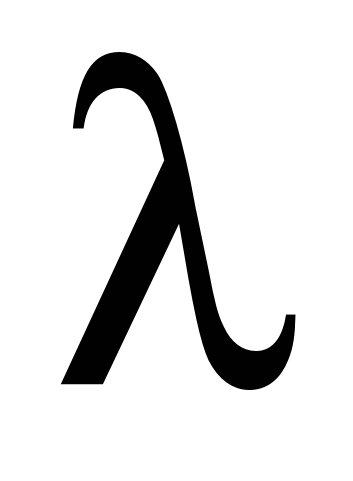 ; б) частные законы распределения случайных величин ; б) частные законы распределения случайных величин 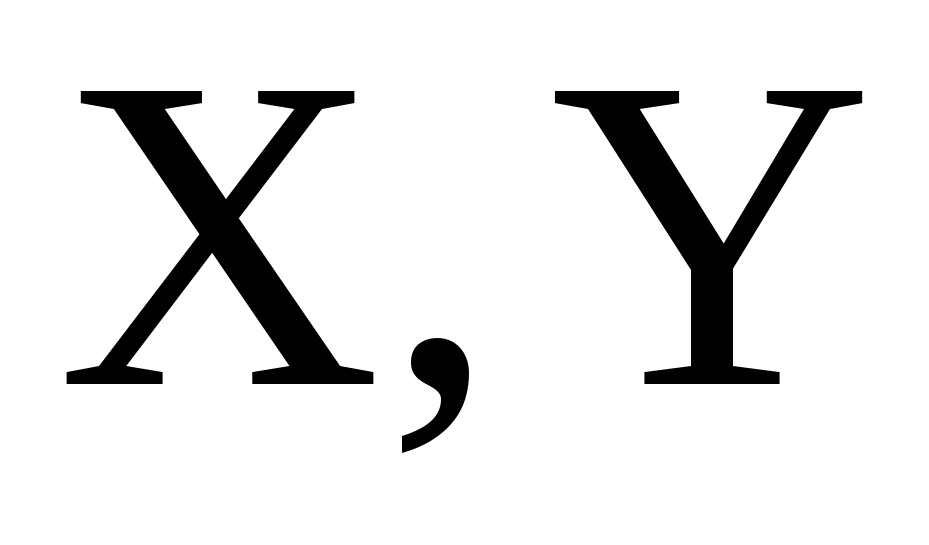 ; ;
в) 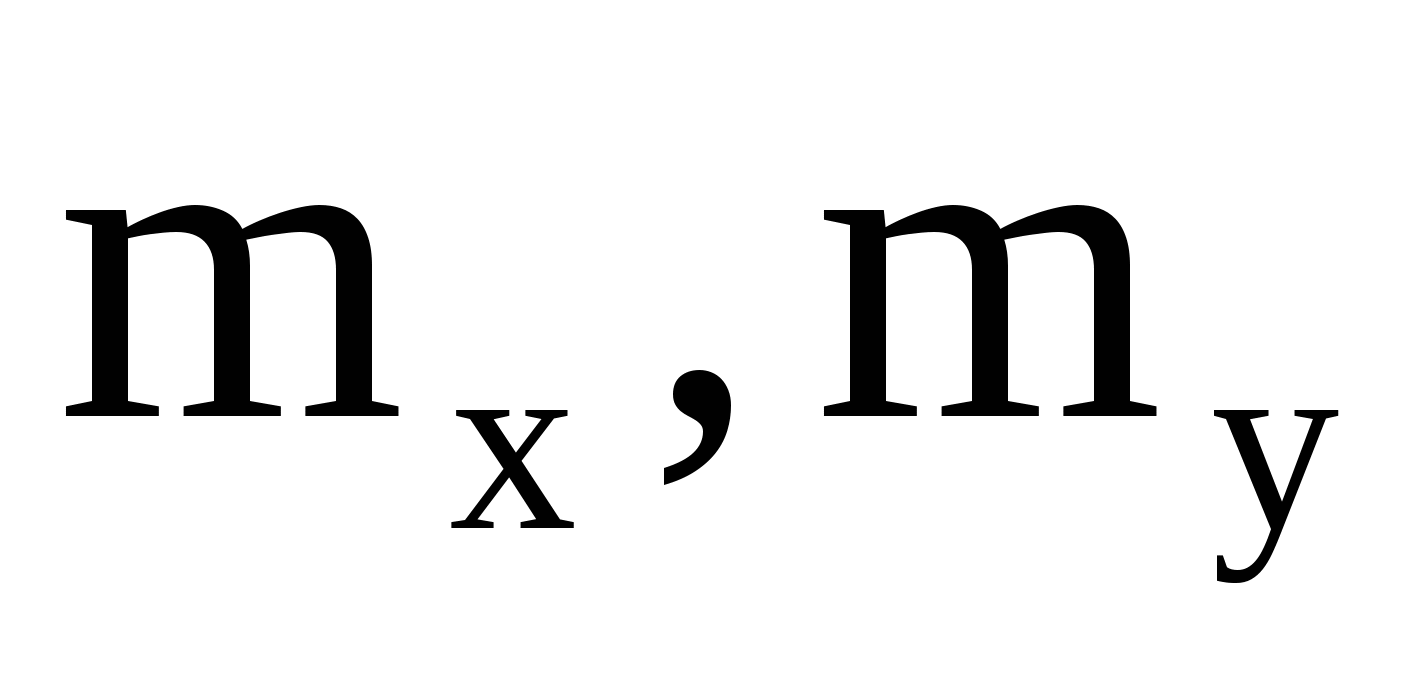 , ,  ; г) коэффициент корреляции ; г) коэффициент корреляции 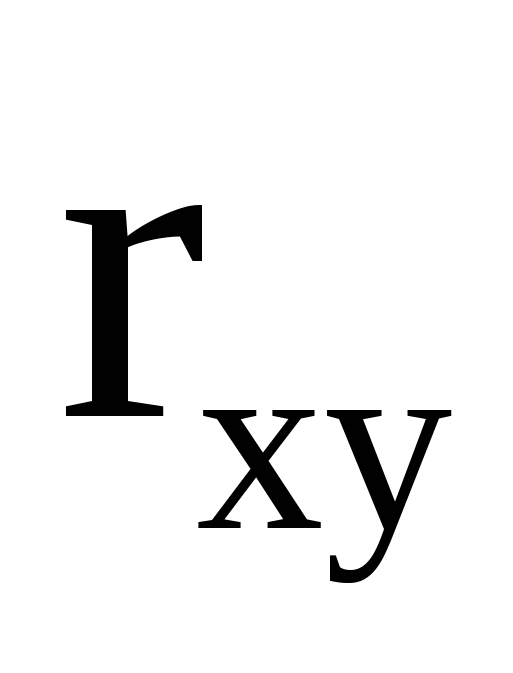 ; д) вероятность попаданий ; д) вероятность попаданий
двумерной случайной величины в область 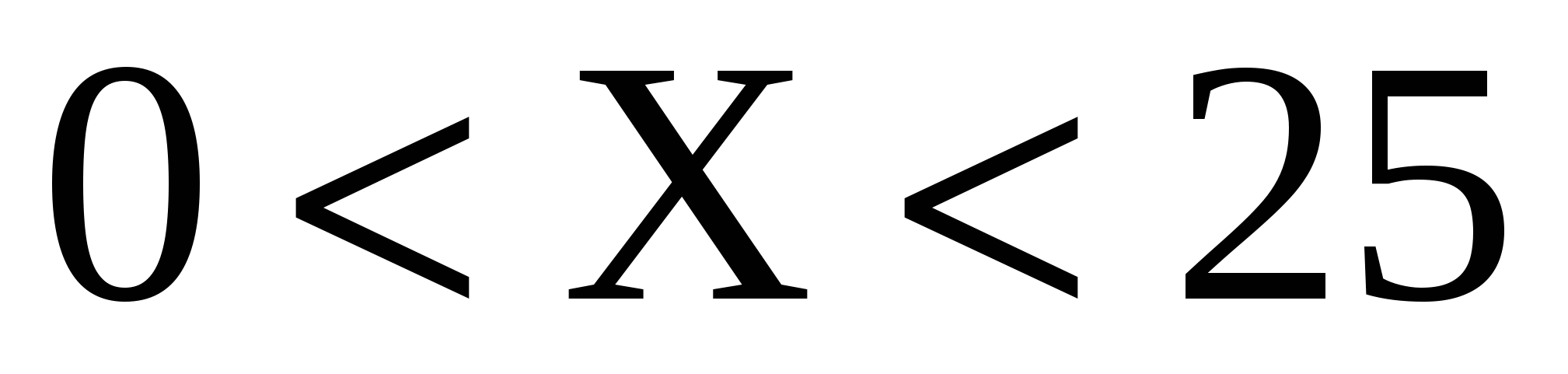 ; ; 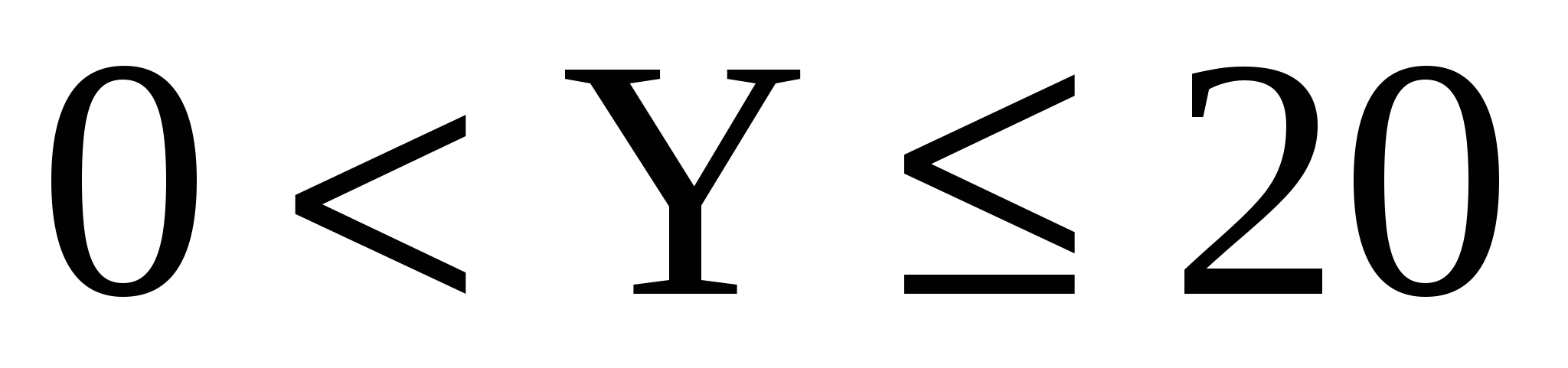 . .
Решение: так как 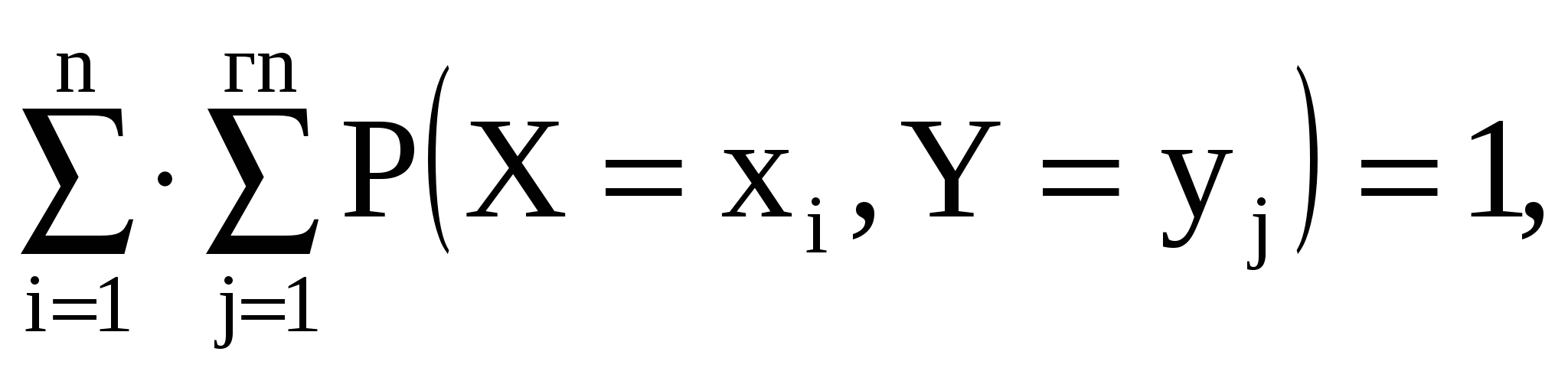
то 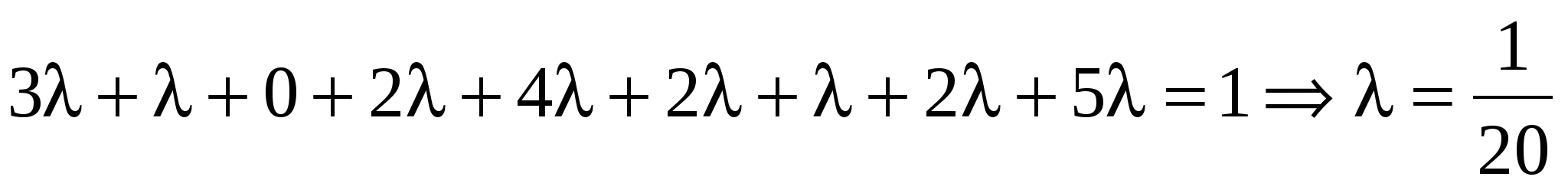 . .
Закон распределения случайной величины X
  Х 10 20 30 Х 10 20 30
Р 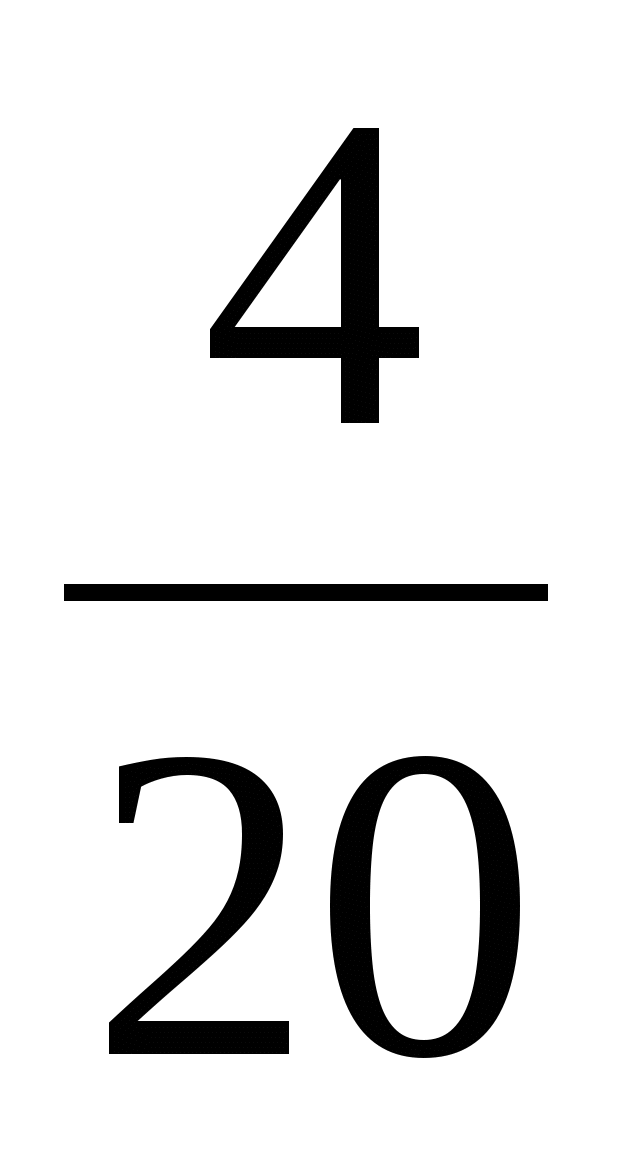 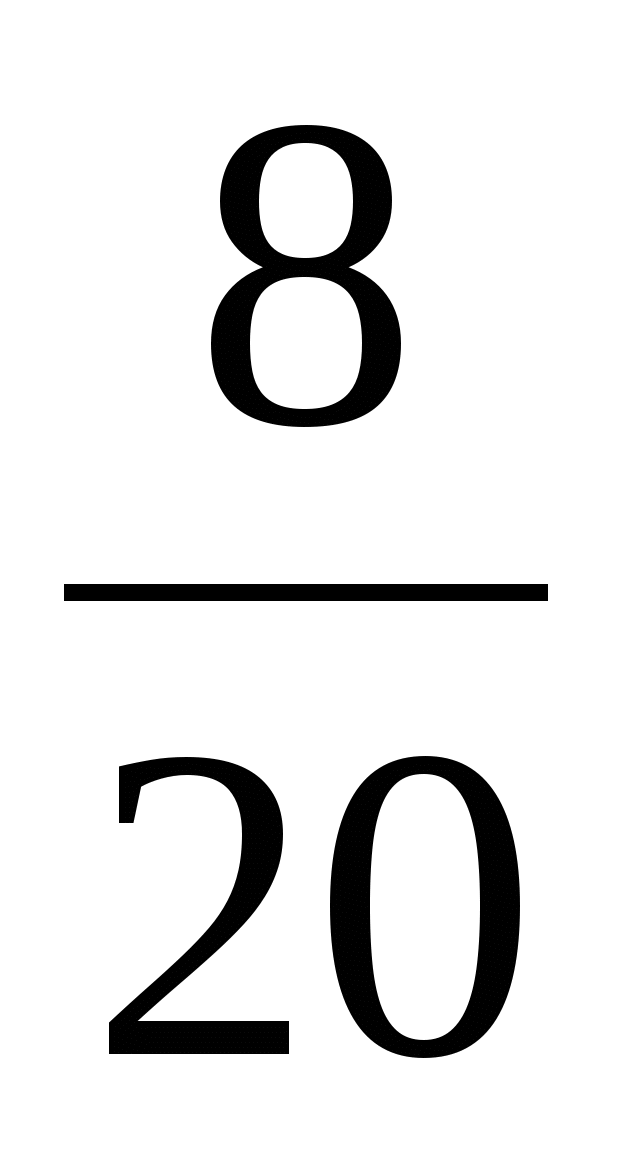 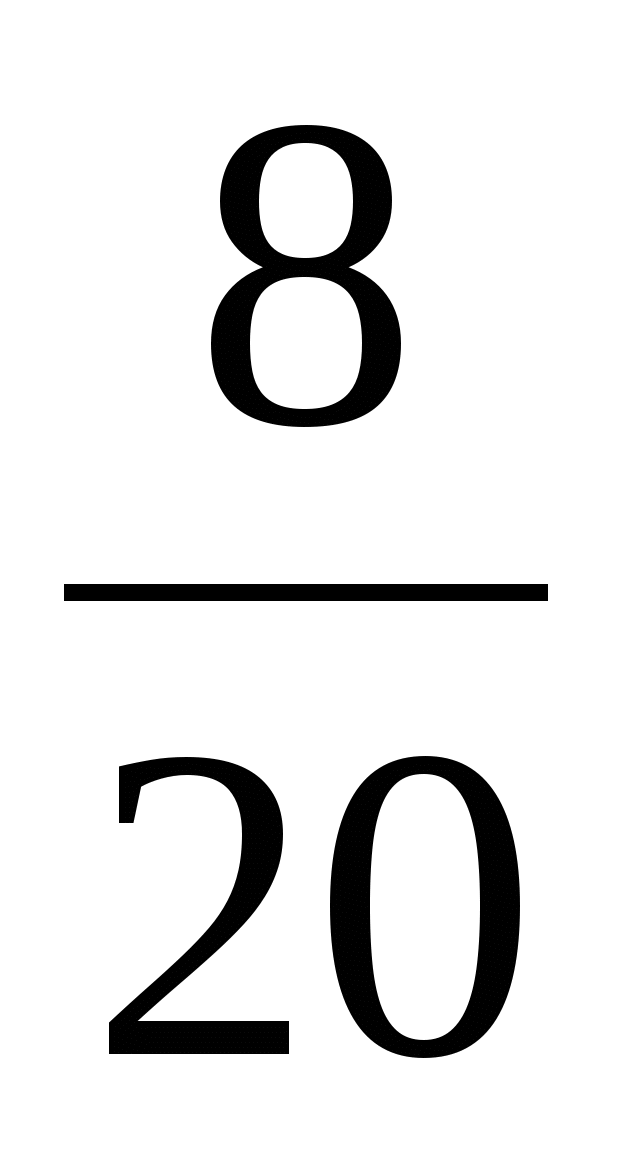 , т. к. , т. к. 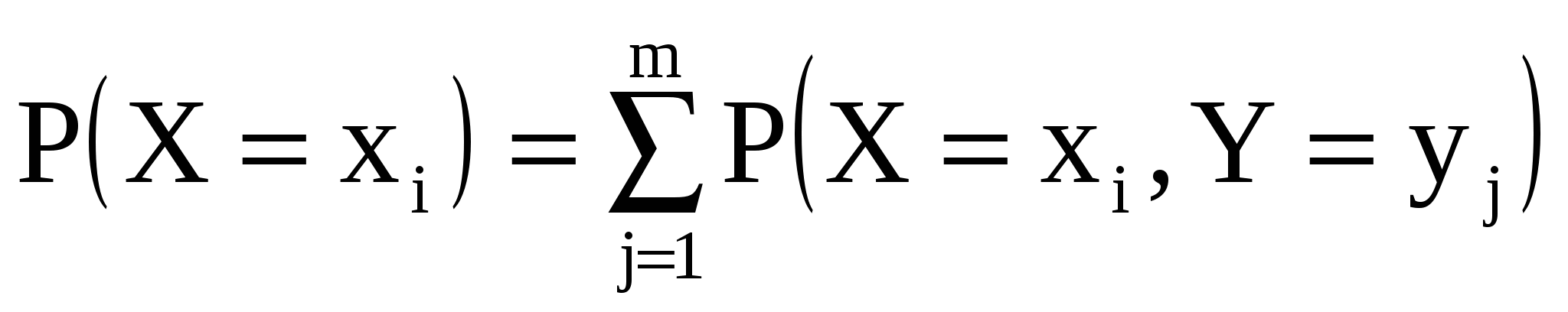 . .
Закон распределения случайной величины Y
  Y 20 40 60 Y 20 40 60
P    . .
Отсюда:
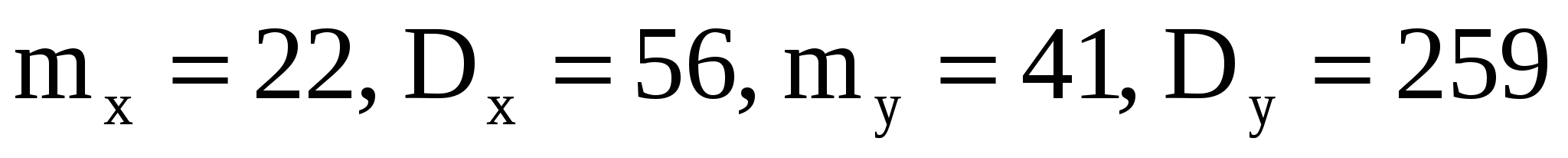
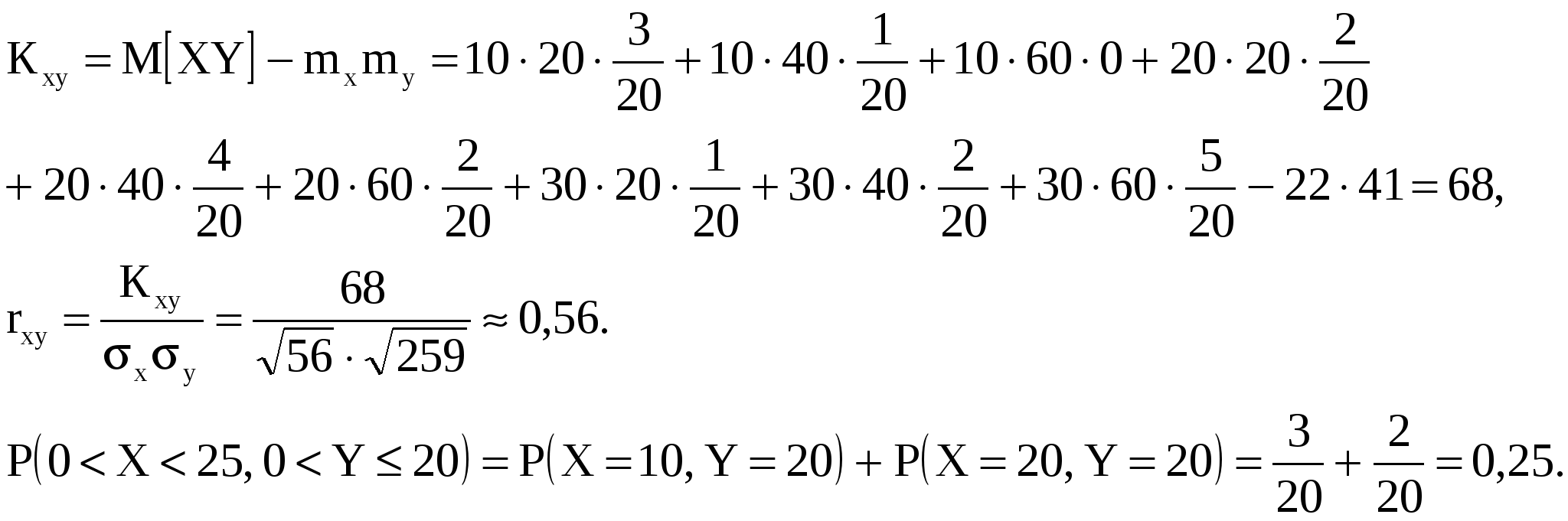
Задача 11. Плотность совместного распределения системы двух случайных величин 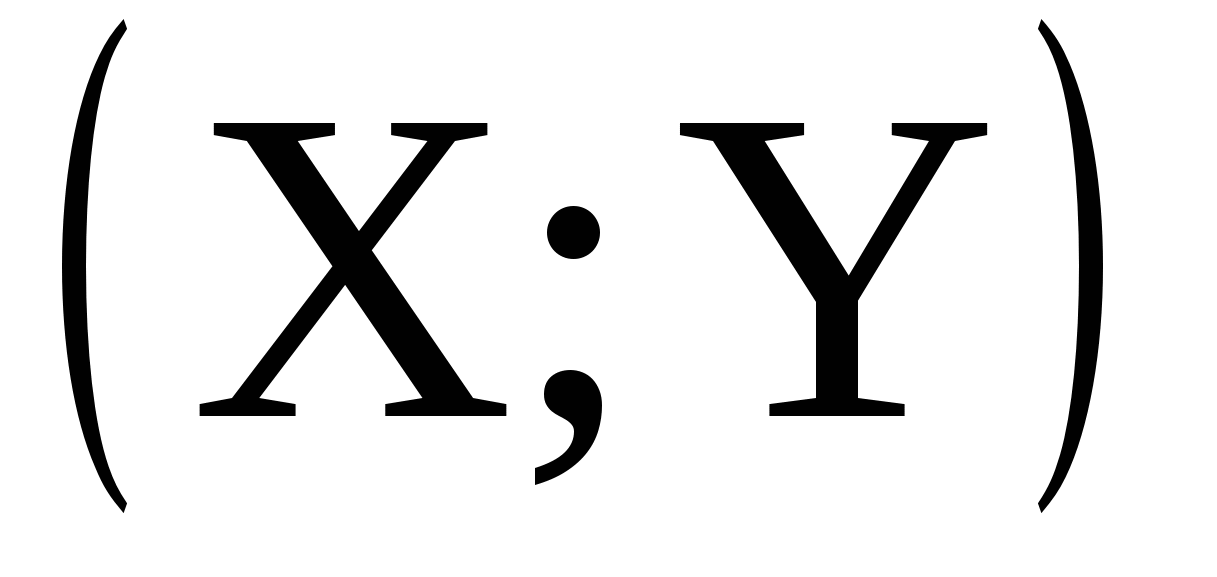 задана выражением задана выражением 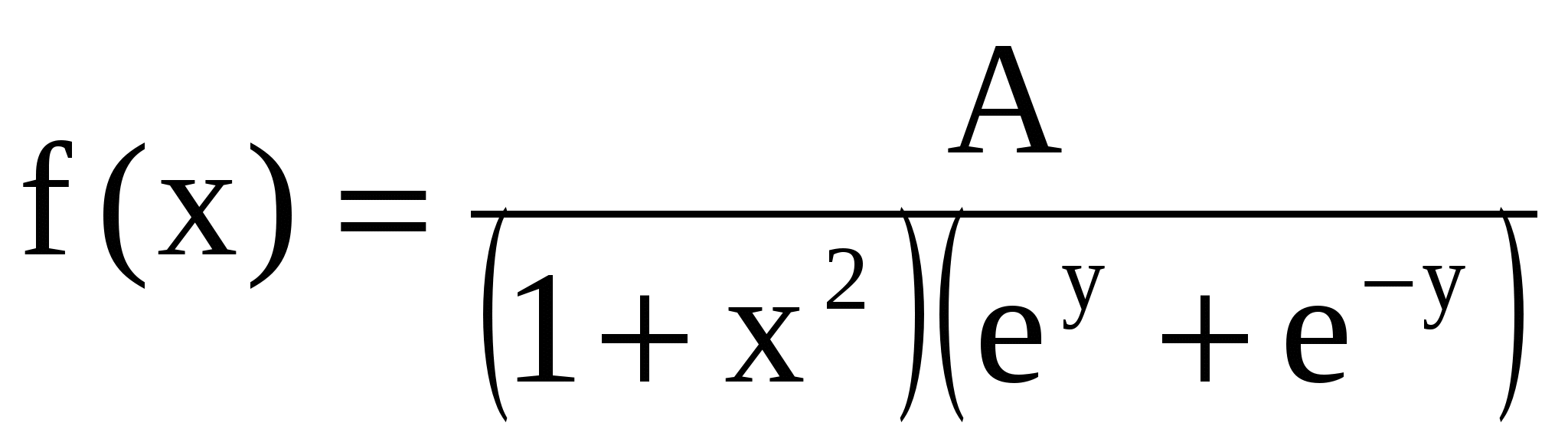 . .
Найти: а) коэффициент А; б) плотности распределения случайных величин 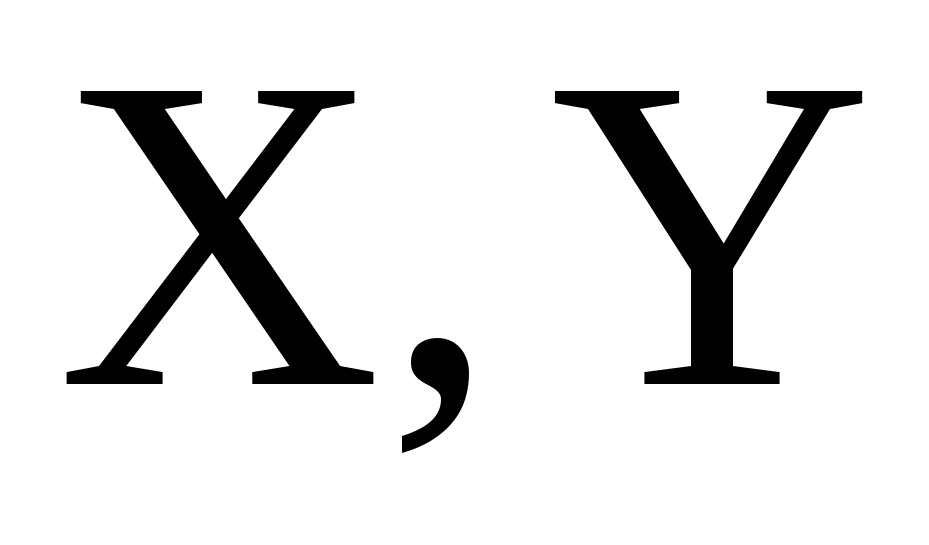 , входящих в систему; в) определить зависимы или независимы случайные величины. , входящих в систему; в) определить зависимы или независимы случайные величины.
Решение. Из основного свойства плотности
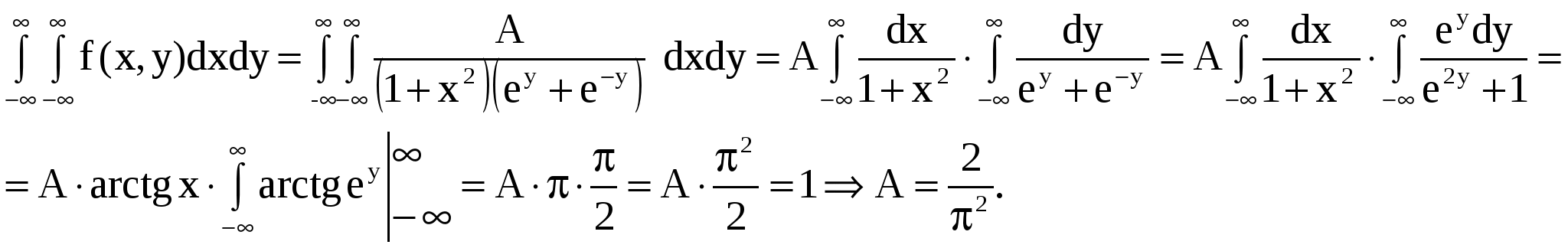
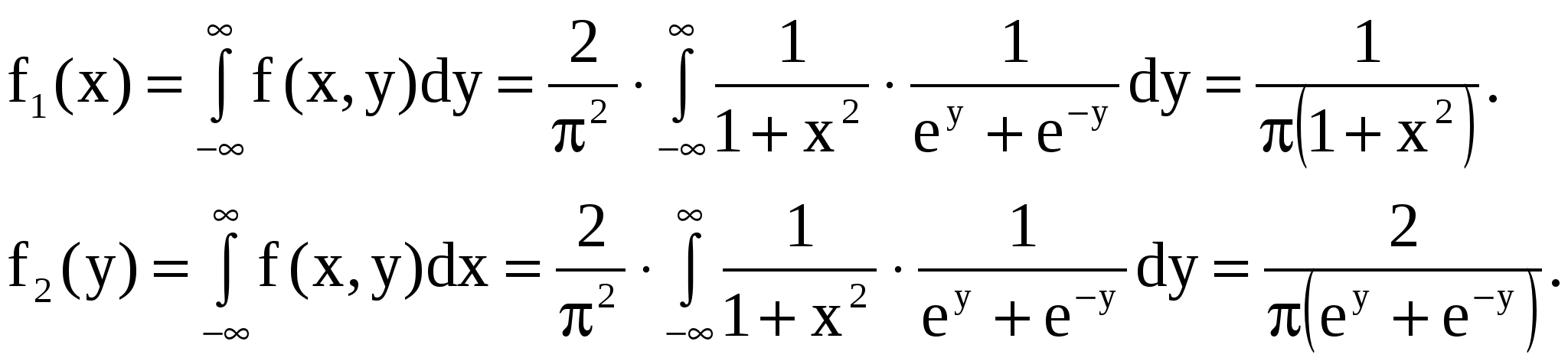
Т.к. 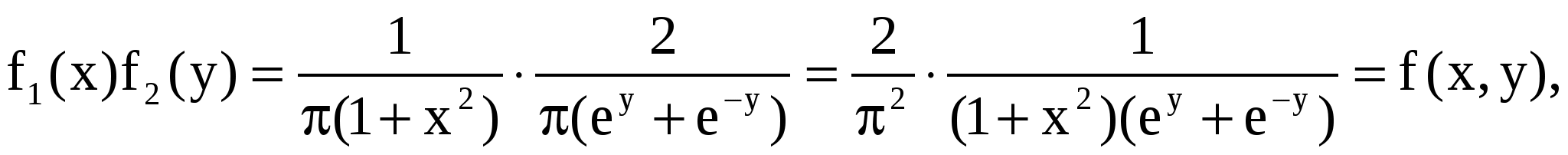
случайные величины 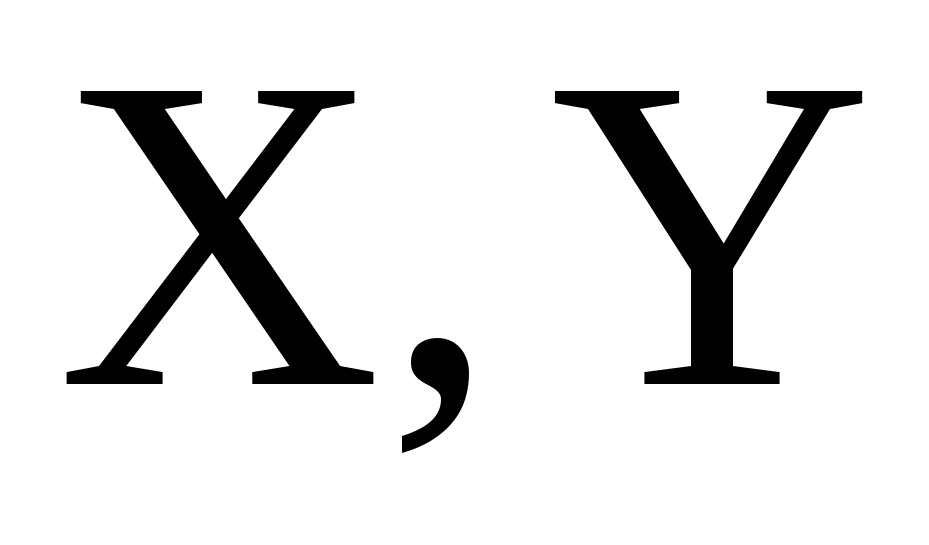 - независимы. - независимы.
|
|
|
 Скачать 1.2 Mb.
Скачать 1.2 Mb. Случайная величина
Случайная величина 
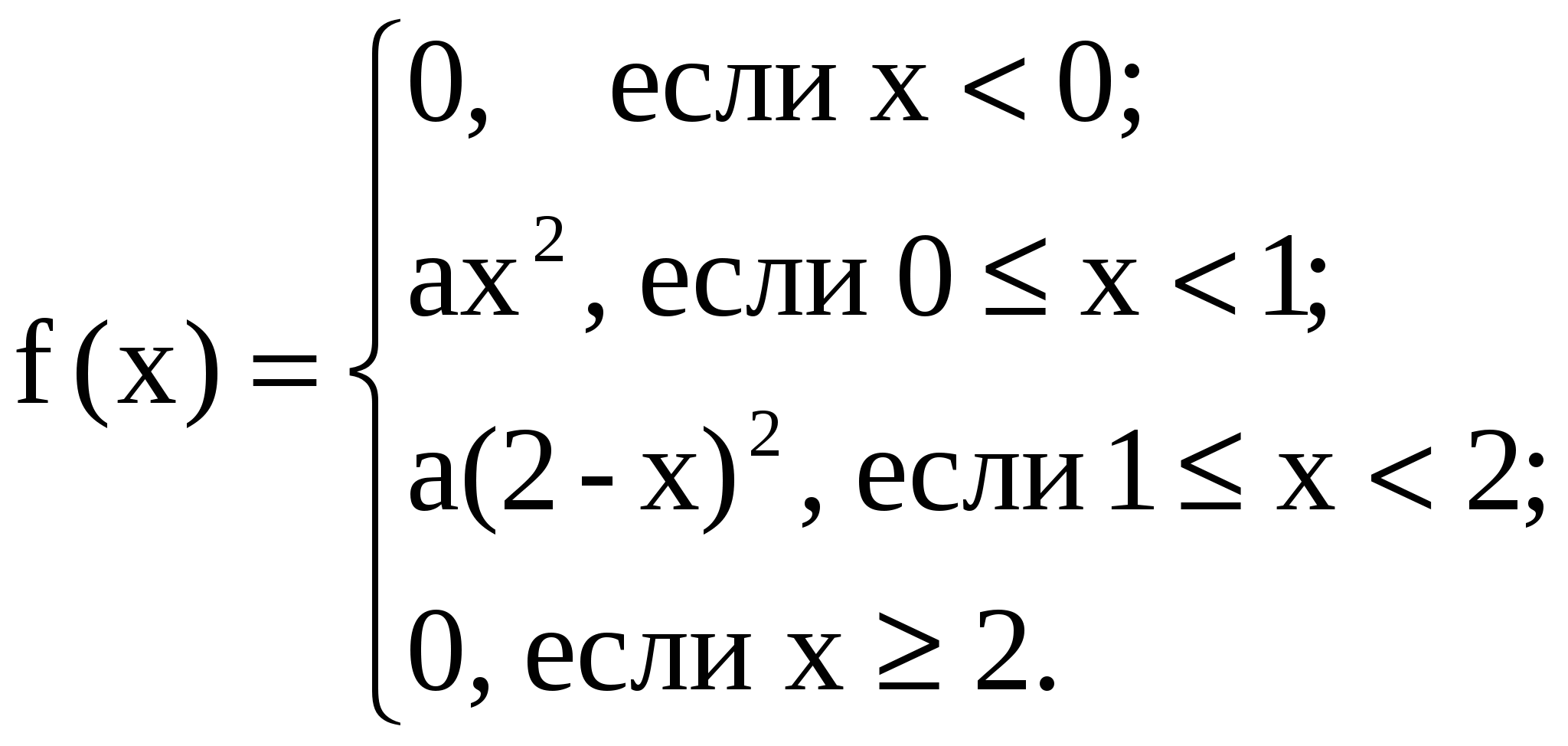
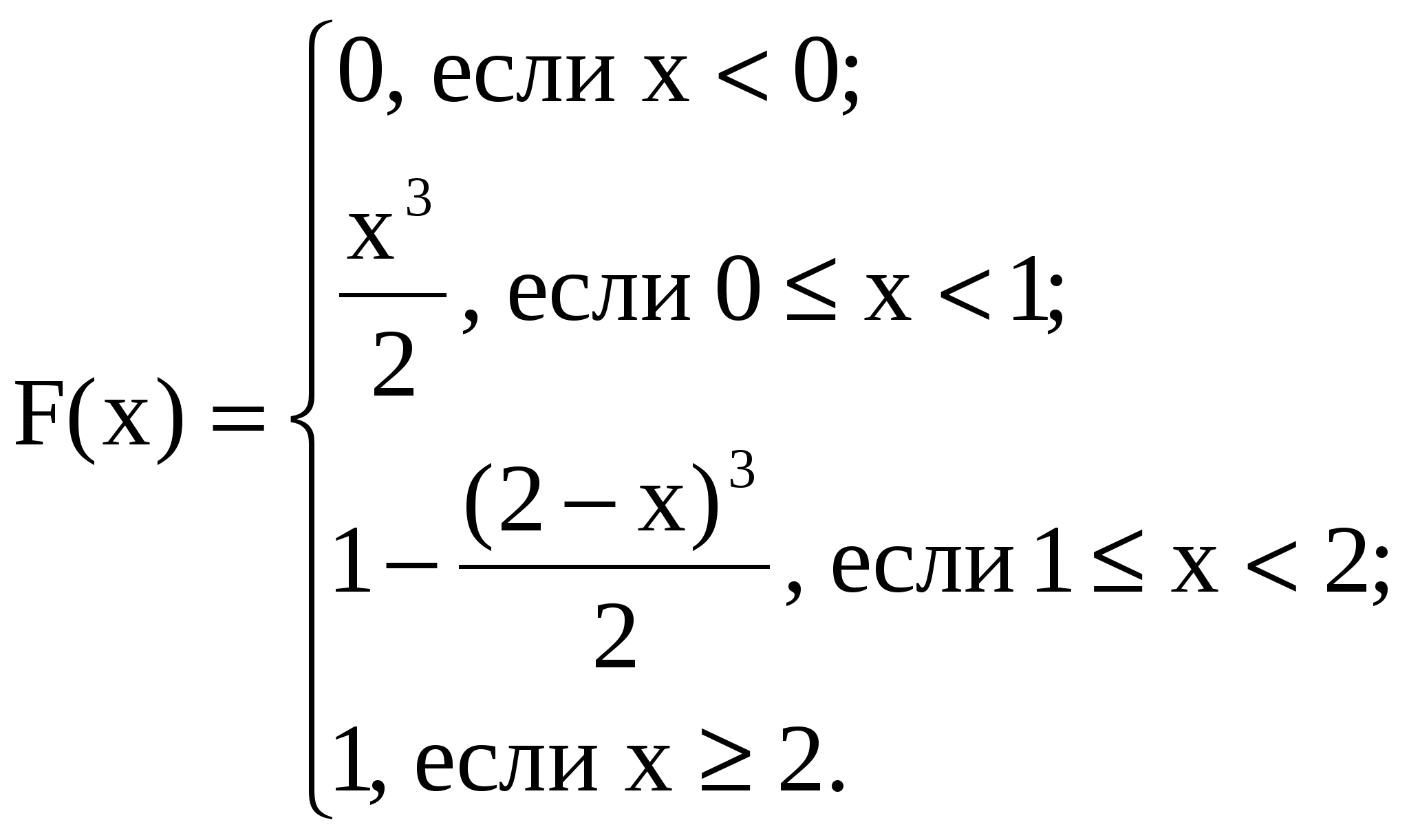
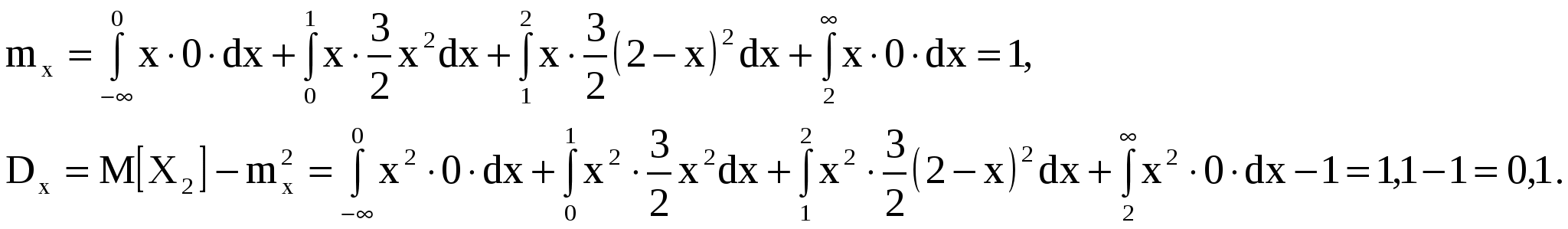



 Ряд распределения случайной величины
Ряд распределения случайной величины 
 Х
Х 

 Задача 10. Закон распределения системы дискретных случайных величин
Задача 10. Закон распределения системы дискретных случайных величин  задан таблицей:
задан таблицей:


 Х 10 20 30
Х 10 20 30
 Y 20 40 60
Y 20 40 60