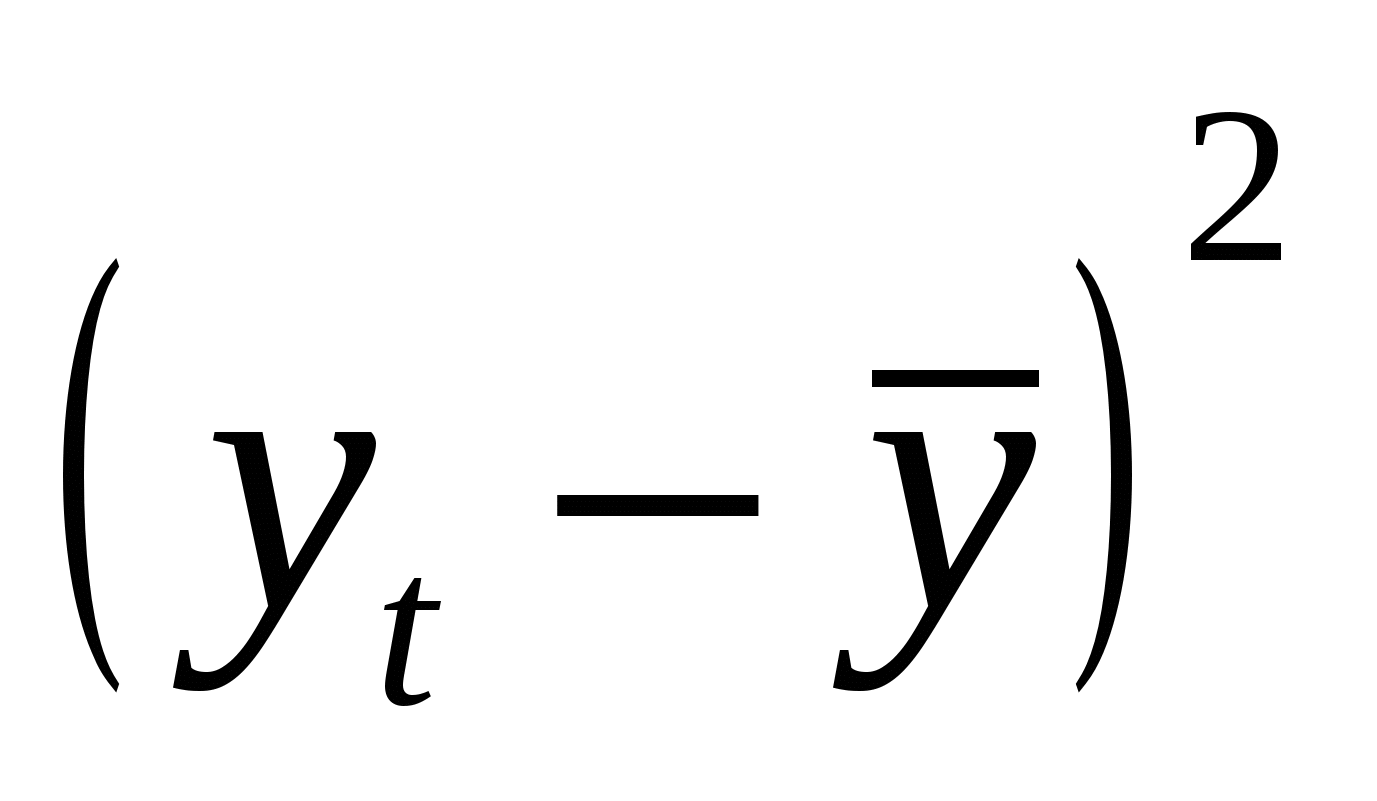Требуется:
Проверить продуктивность технологической матрицы А=(aij) (матрицы коэффициентов прямых материальных затрат).
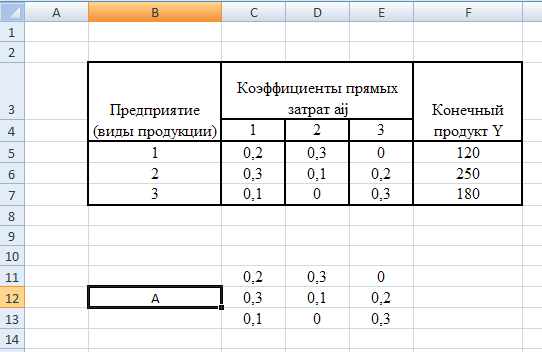
Построить баланс (заполнить таблицу) производства и распределения продукции предприятий холдинга.
Предприятие (виды продукции)
|
Коэффициенты прямых затрат aij
|
Конечный продукт Y
|
1
|
2
|
3
|
1
|
0,2
|
0,3
|
0
|
120
|
2
|
0,3
|
0,1
|
0,2
|
250
|
3
|
0,1
|
0
|
0,3
|
180
|
Решение
1) Проверить продуктивность технологической матрицы A=(аij) (матрицы коэффициентов прямых материальных затрат).
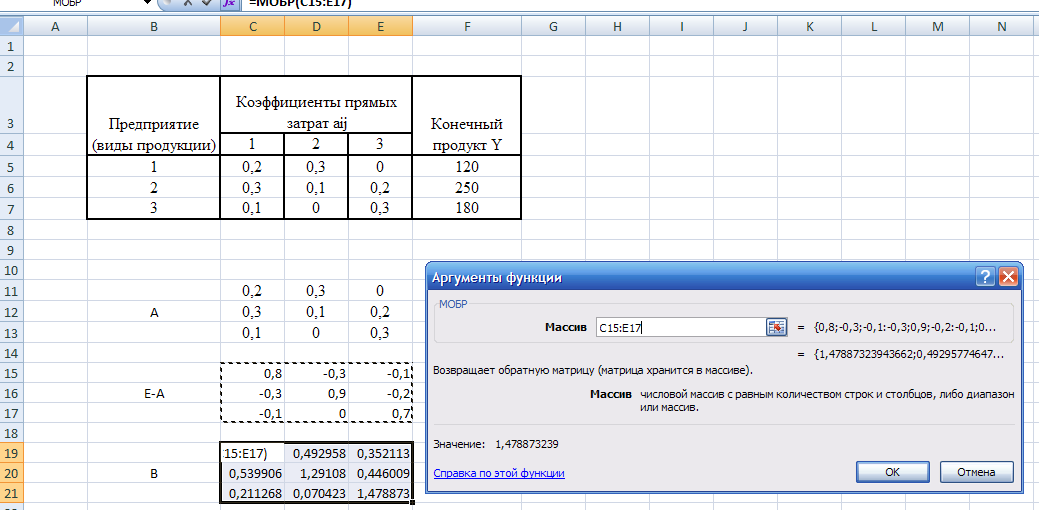
1.1. Для решения данной экономической задачи будет выбрана среда табличного процессора MS Excel. (рис. 3.1)
Рис. 3.1
Исходные данные
1.2. Найдем разность между единичной матрицей Е и матрицей А.
Для этого воспользуемся правилом вычитания матриц одинаковой размерности. 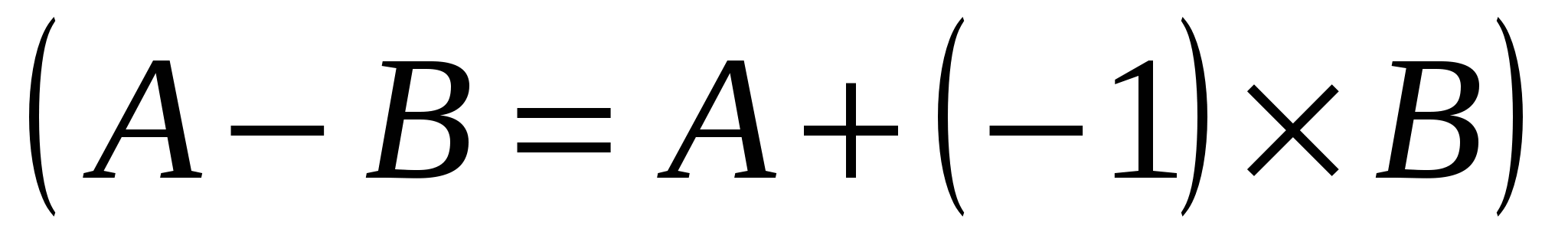 (рис. 3.2) (рис. 3.2)
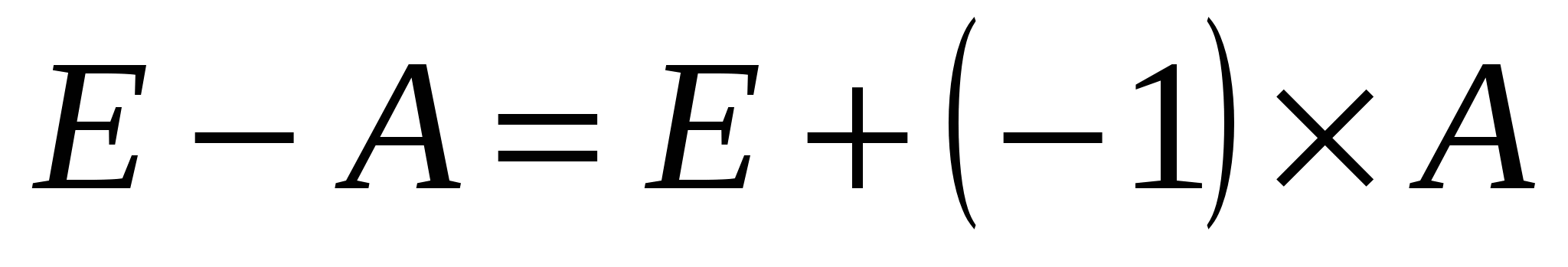
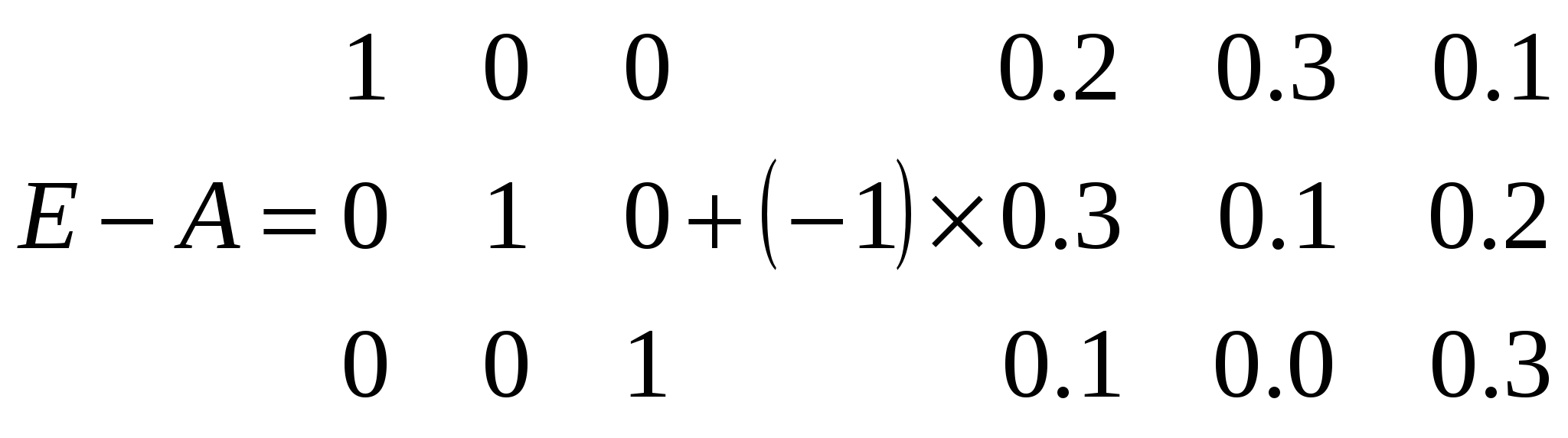
|
0,8
|
-0,3
|
-0,1
|
E-A
|
-0,3
|
0,9
|
-0,2
|
|
-0,1
|
0
|
0,7
|
1.3. Найдем обратную матрицу 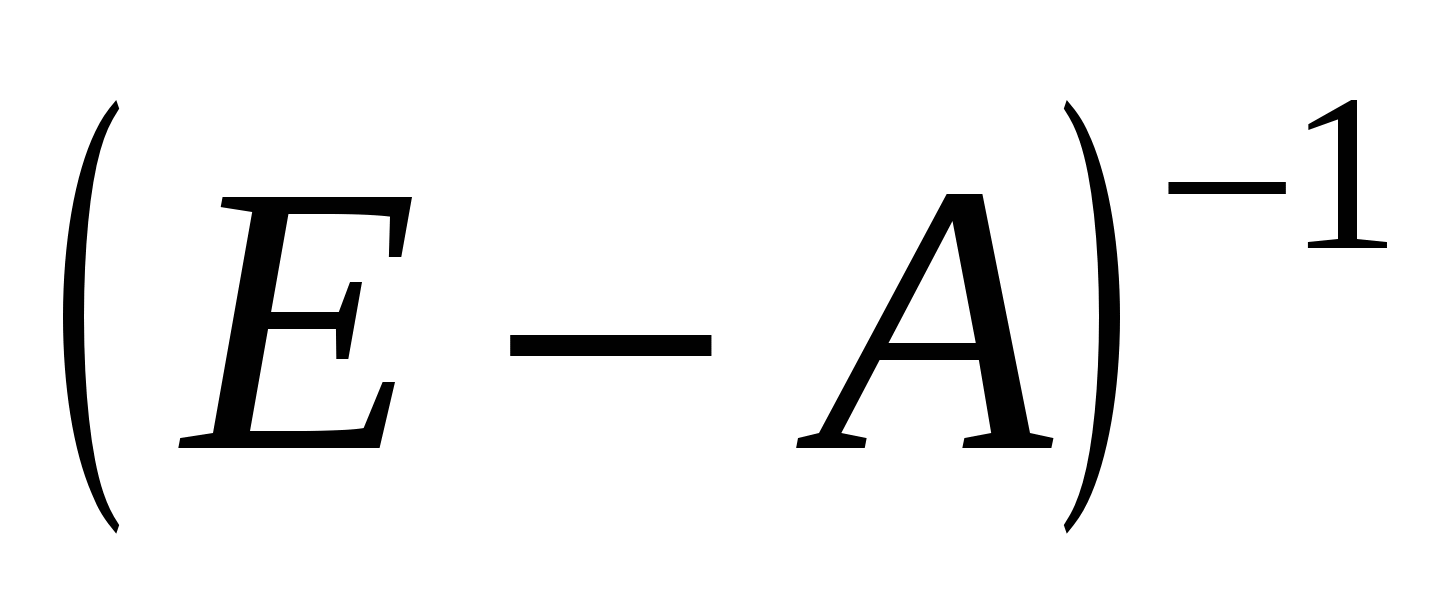 . Воспользуемся встроенными функциями MS Excel (математические, обратная матрица) (рис. 3.2). . Воспользуемся встроенными функциями MS Excel (математические, обратная матрица) (рис. 3.2).
Рис 3.2
1.4. Чтобы определить Валовую продукцию (матрицу ), надо матрицу ), надо матрицу 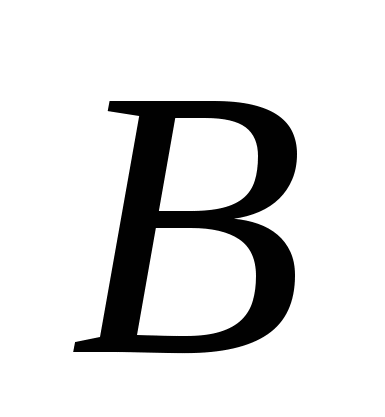 = =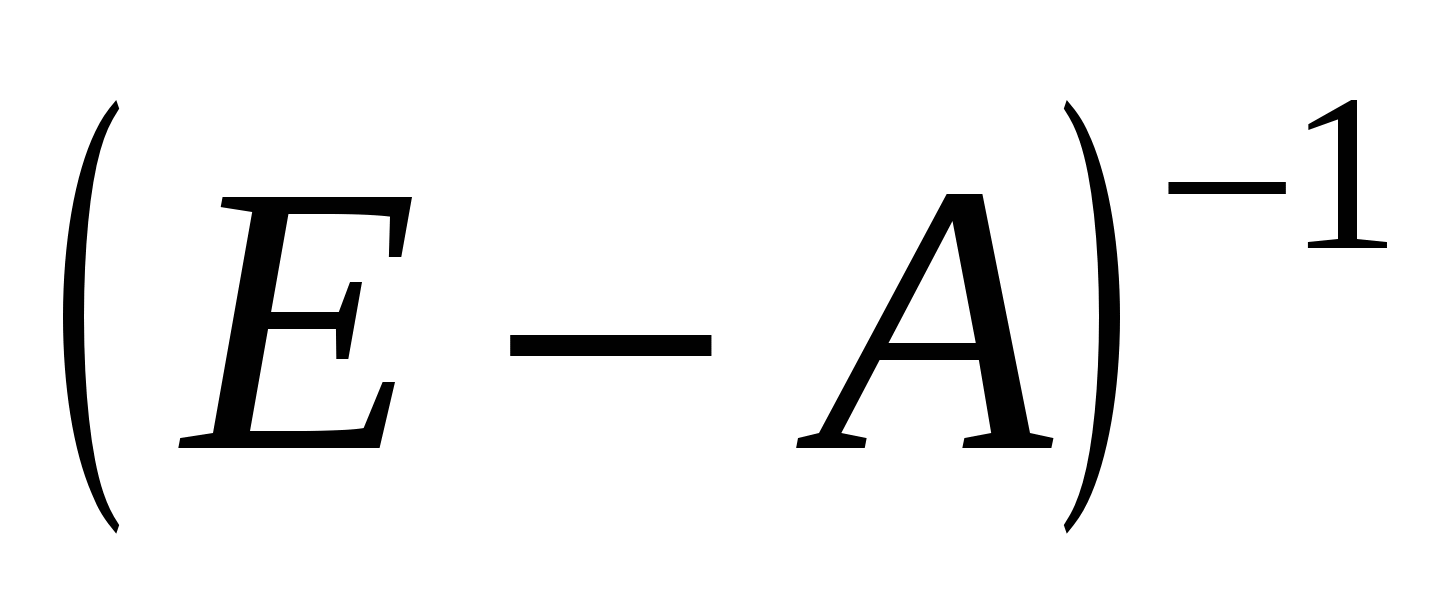 умножить на Конечный продукт (матрицу умножить на Конечный продукт (матрицу 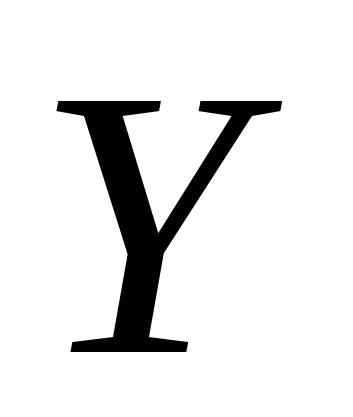 ). Воспользуемся опять встроенными функциями MS Excel (математические, умножение матриц) (рис. 3.3). ). Воспользуемся опять встроенными функциями MS Excel (математические, умножение матриц) (рис. 3.3).
Рис. 3.3
Определение валовой продукции (матрица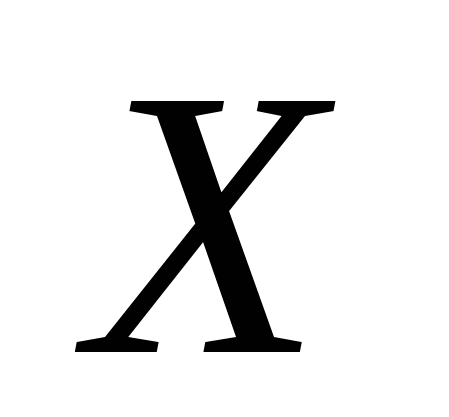 ) )
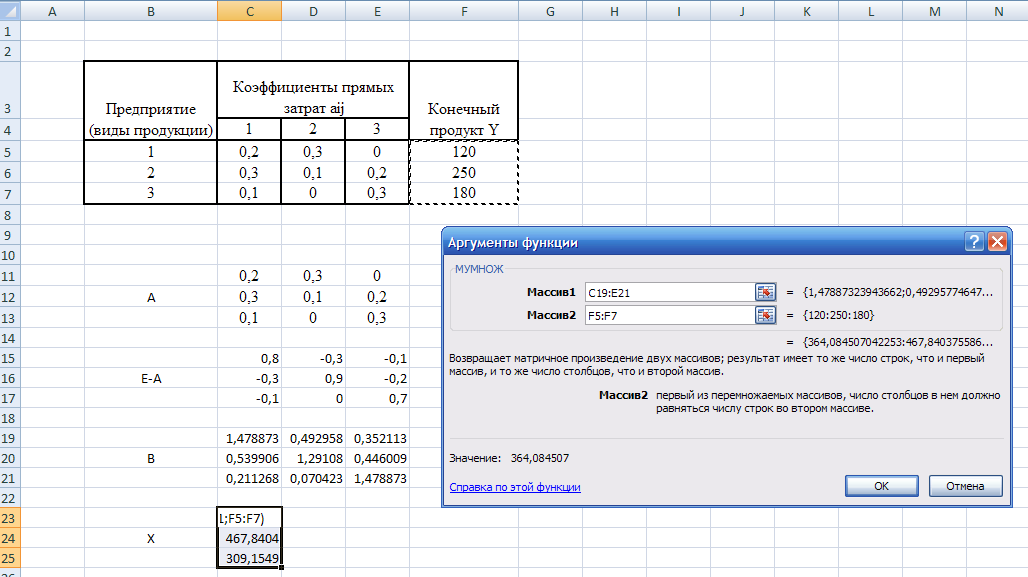
1.5. Матрица  (матрица коэффициентов прямых материальных затрат) продуктивна, т.к. существует неотрицательный вектор (матрица коэффициентов прямых материальных затрат) продуктивна, т.к. существует неотрицательный вектор 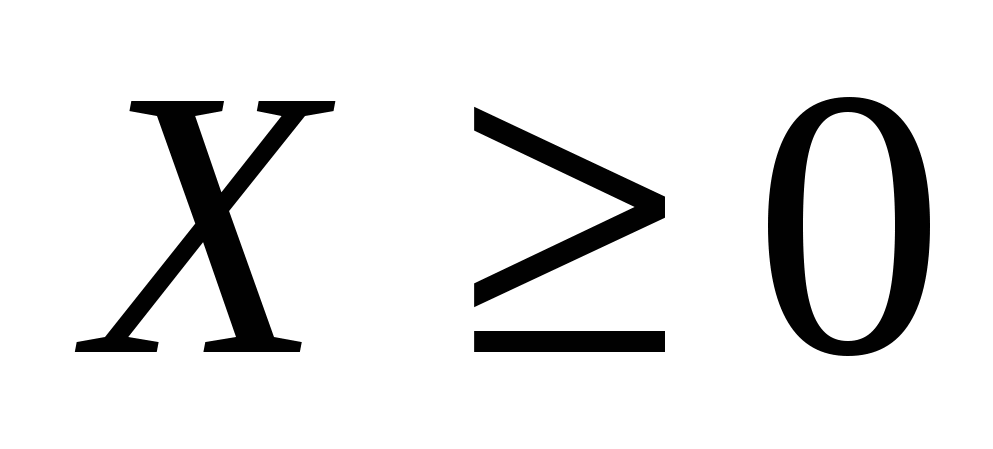 . .
2) Построить баланс (заполнить таблицу) производства и распределения продукции предприятий холдинга.
2.1. Для распределения продукции предприятий холдинга необходимо найти 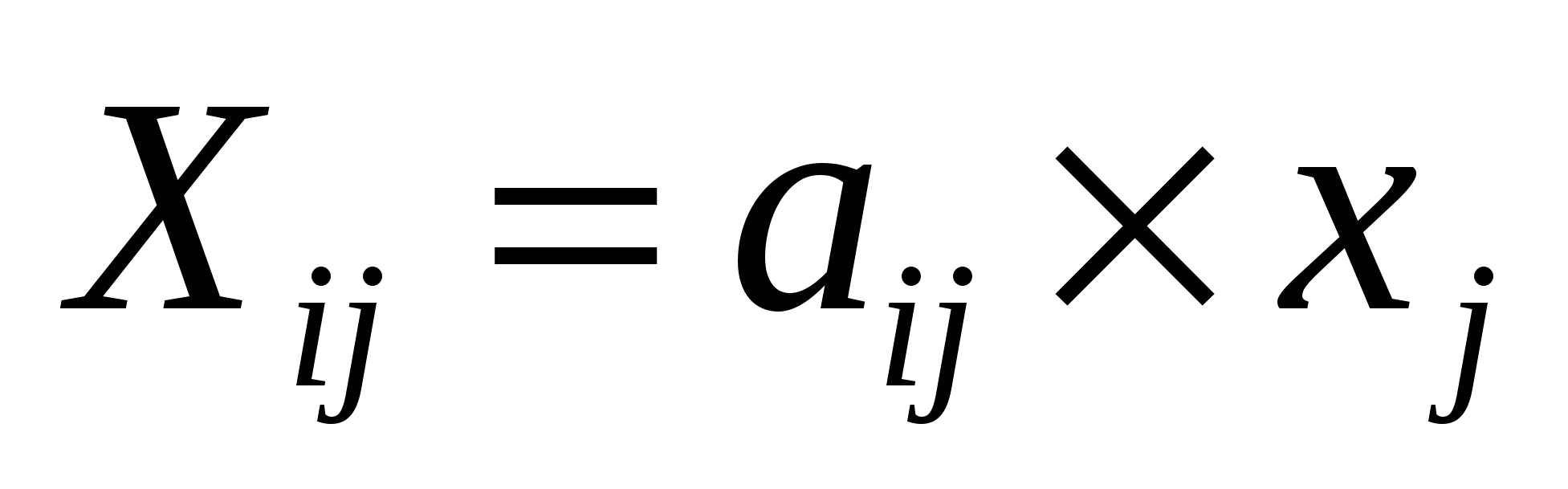 (рис. 3.4) (рис. 3.4)
Рис. 3.4
Распределение продукции предприятий холдинга
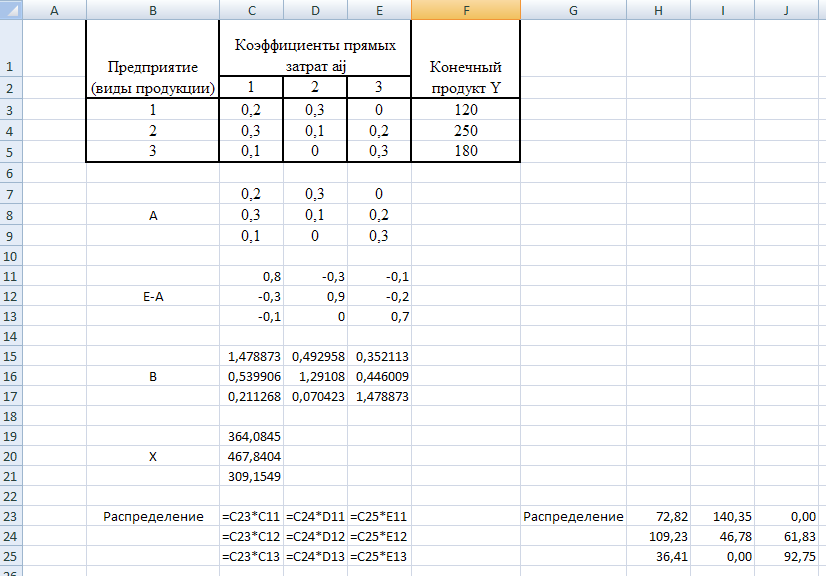
2.2. Построим межотраслевой баланс производства (рис. 3.5)
Рис 3.5
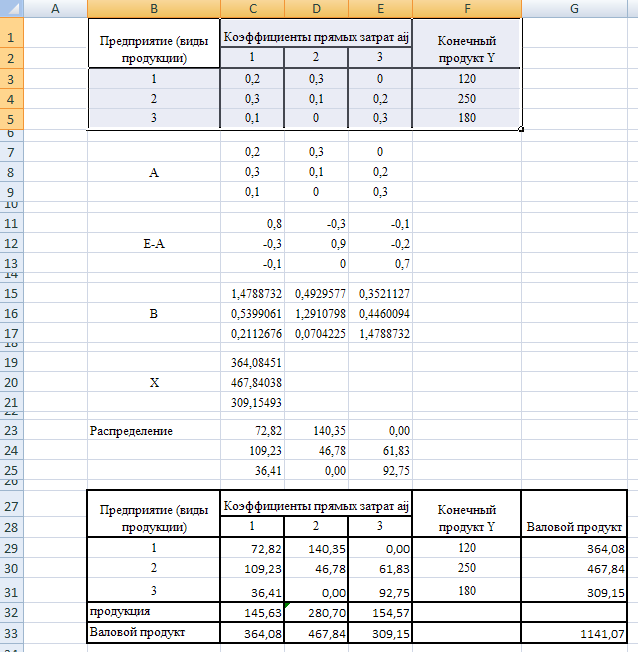
Условно чистая продукция – это разность между валовым продуктом и суммой продуктов, которые потребляет каждая отрасль.
Ответ:
1) Матрица  (матрица коэффициентов прямых материальных затрат) продуктивна, т.к. существует неотрицательный вектор (матрица коэффициентов прямых материальных затрат) продуктивна, т.к. существует неотрицательный вектор 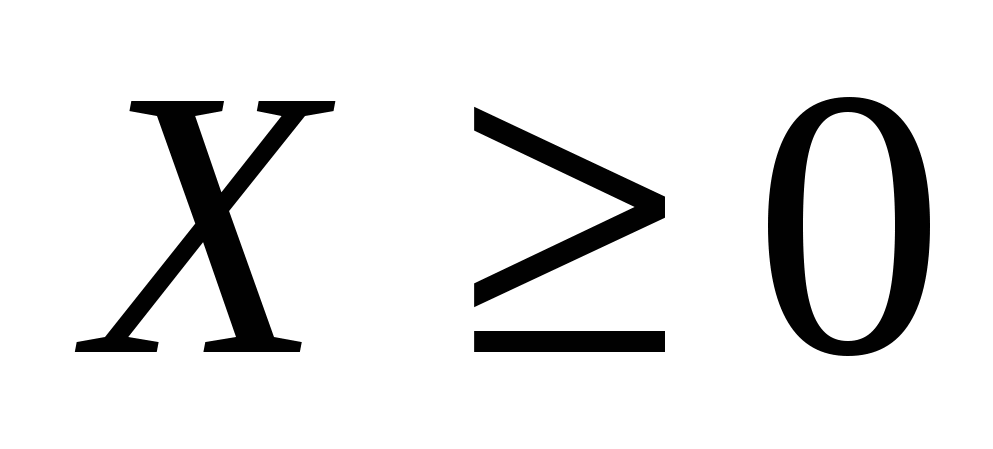 . .
2)
Межотраслевой баланс
|
Предприятие (виды продукции)
|
Коэффициенты прямых затрат aij
|
Конечный продукт Y
|
Валовой продукт
|
1
|
2
|
3
|
1
|
72,82
|
140,35
|
0,00
|
120
|
364,08
|
2
|
109,23
|
46,78
|
61,83
|
250
|
467,84
|
3
|
36,41
|
0,00
|
92,75
|
180
|
309,15
|
Условно чистая продукция
|
145,63
|
280,70
|
154,57
|
|
|
Валовой продукт
|
364,08
|
467,84
|
309,15
|
|
1141,07
|
Задача 4
Исследовать динамику экономического показателя на основе анализа одномерного временного ряда.
В течение девяти последовательных недель фиксировался спрос Y(t) (млн руб.) на кредитные ресурсы финансовой компании. Временной ряд Y(t) этого показателя приведен в таблице.
-
Номер наблюдения ( t = 1,2,…,9)
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
5
|
7
|
10
|
12
|
15
|
18
|
20
|
23
|
26
|
Требуется:
Проверить наличие аномальных наблюдений.
Построить линейную модель Y(t) = a0 + a1t, параметры которой оценить МНК (Y(t)) – расчетные, смоделированные значения временного ряда).
Оценить адекватность построенных моделей, используя свойства независимости остаточной компоненты, случайности и соответствия нормальному закону распределения (при использовании R/S–критерия взять табулированные границы 2,7-3,7).
Оценить точность моделей на основе использования средней относительной ошибки аппроксимации.
По двум построенным моделям осуществить прогноз спроса на следующие две недели (доверительный интервал прогноза рассчитать при доверительной вероятности p = 70%)
Фактические значения показателя, результаты моделирования и прогнозирования представить графически.
Решение
1). Наличие аномальных наблюдений приводит к искажению результатов моделирования, поэтому необходимо убедиться в отсутствии аномальных данных. Для этого воспользуемся методом Ирвина и найдем характеристическое число (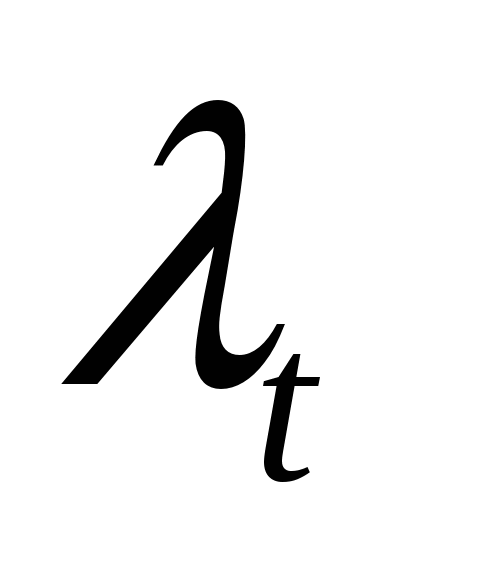 ) (таблица 4.1). ) (таблица 4.1).
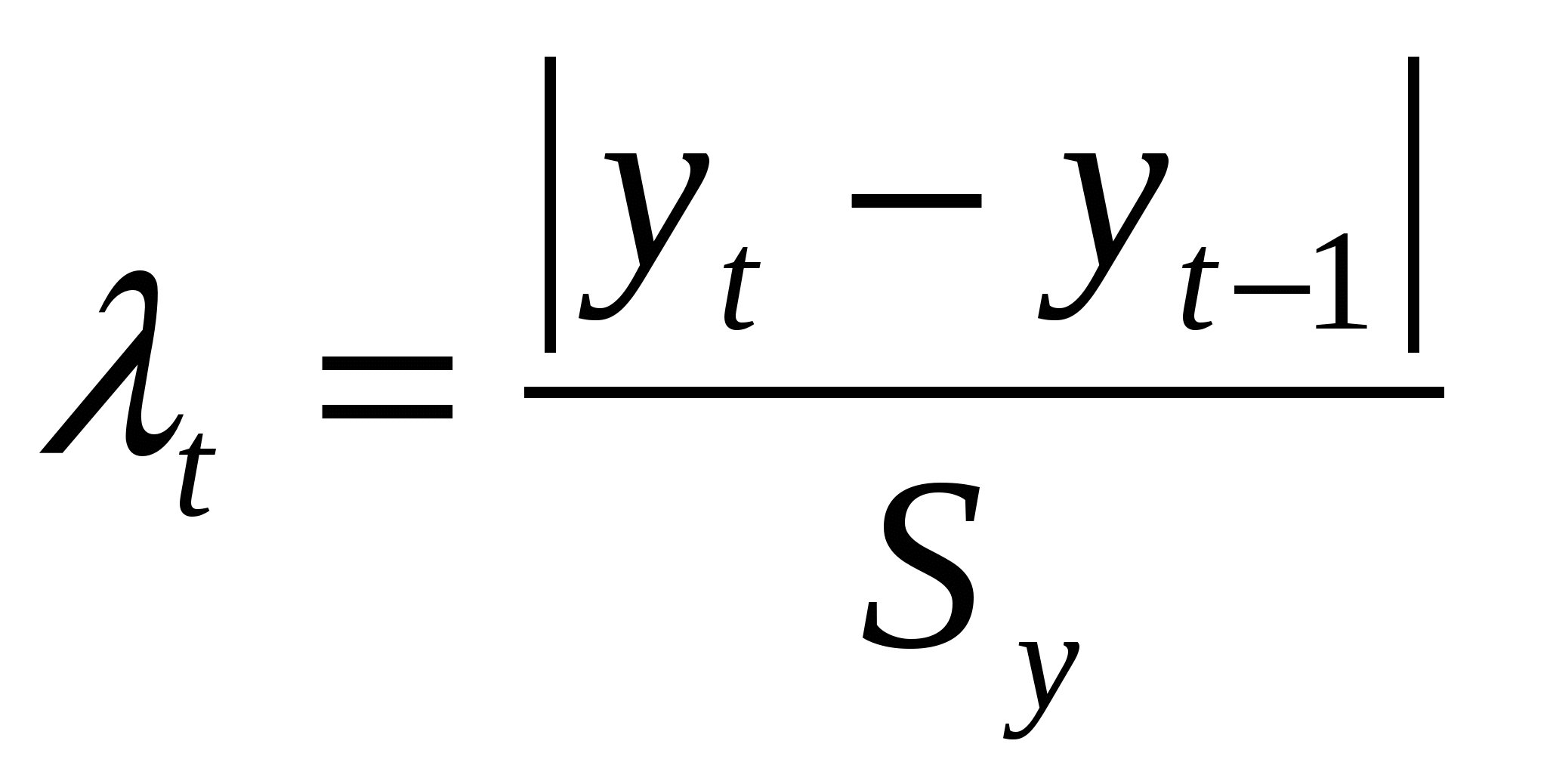 ; ; 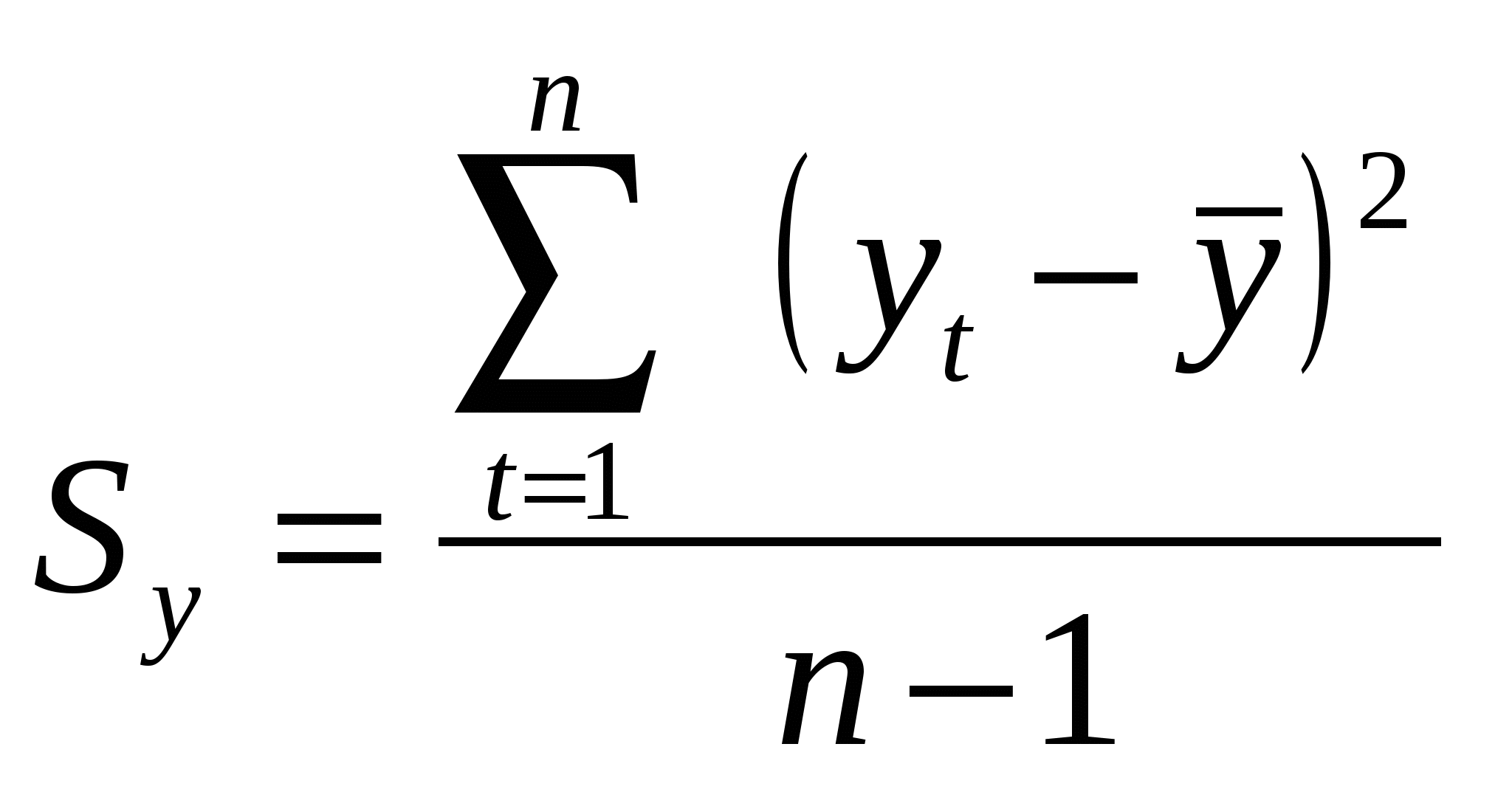 , , 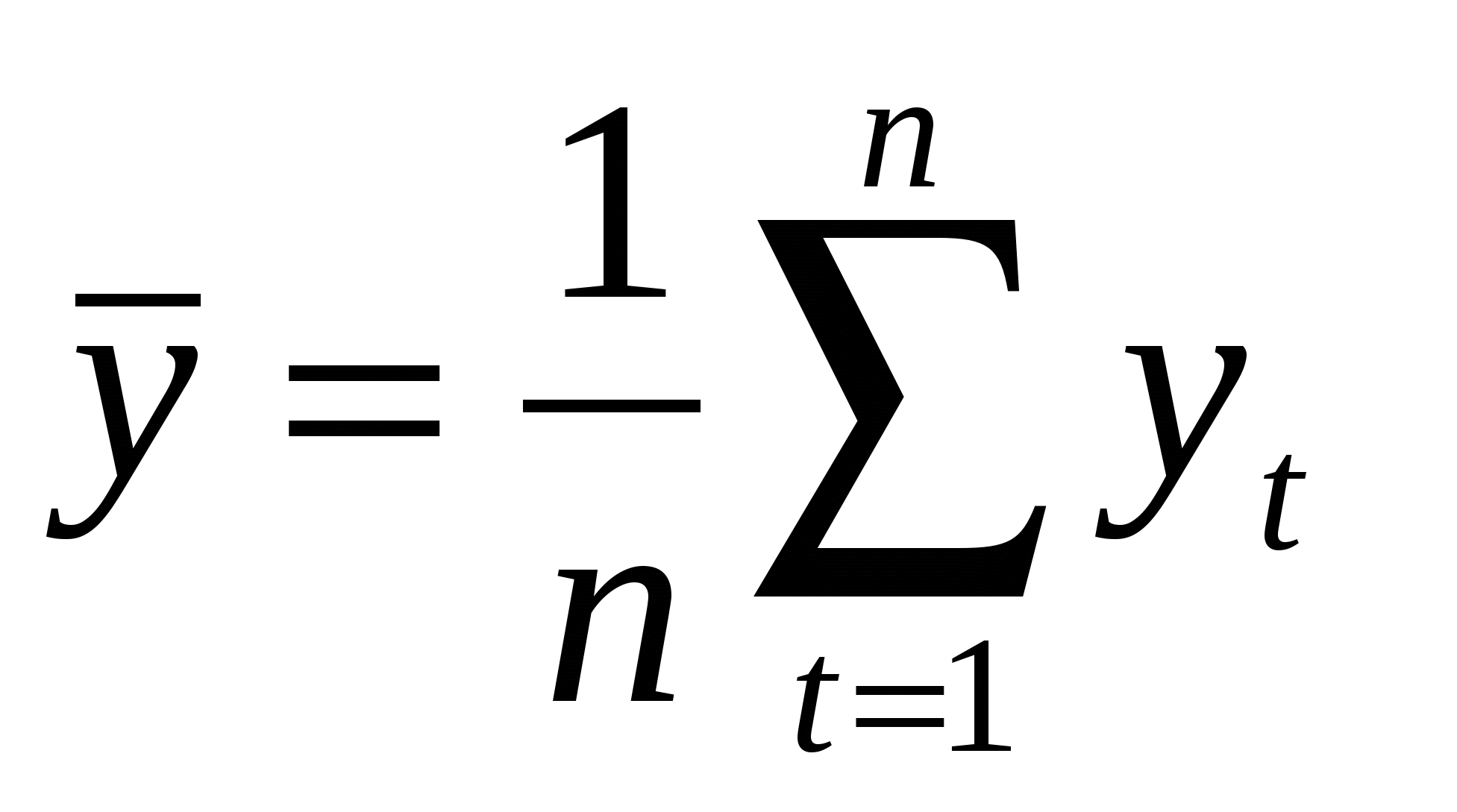
Расчетные значения сравниваются с табличными значениями критерия Ирвина, и если они оказываются больше табличных, то соответствующее значение 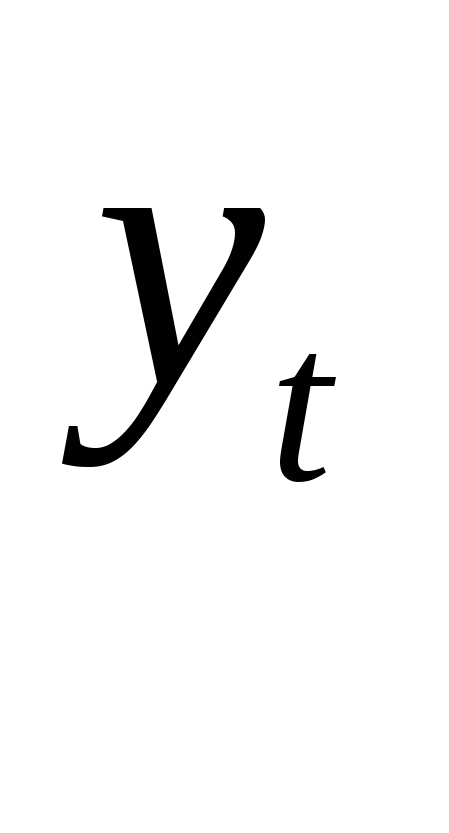 уровня ряда считается аномальным. уровня ряда считается аномальным.
Таблица 4.1
|
t
|
Y
|
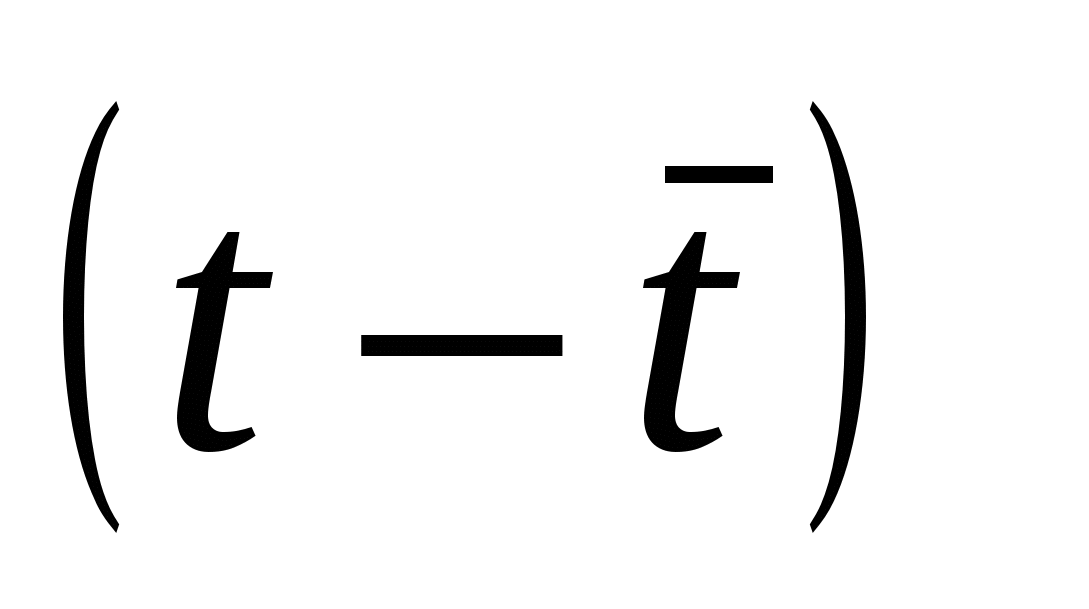
|
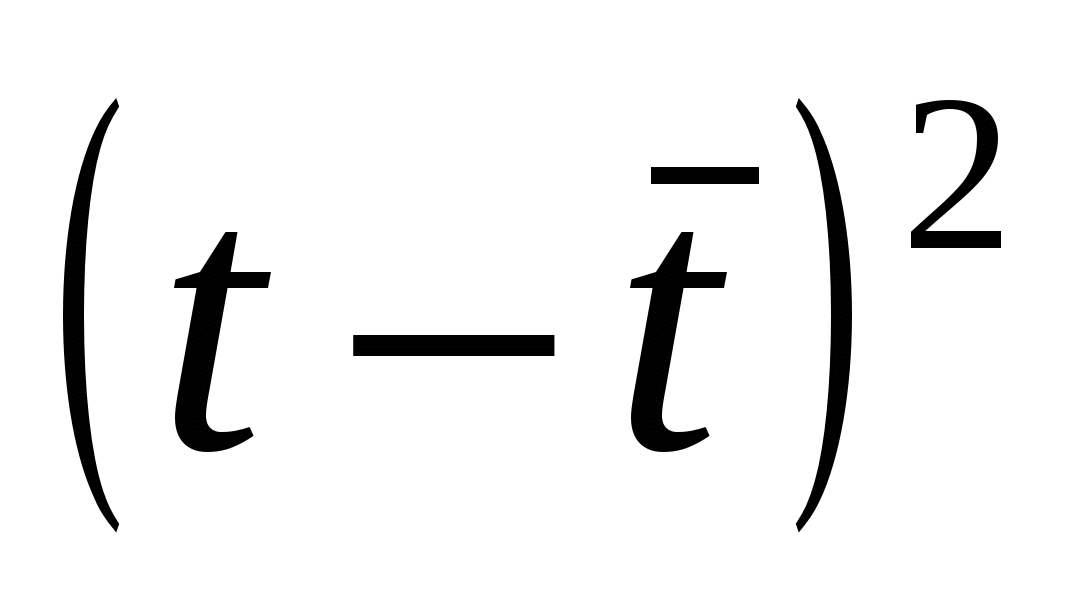
|
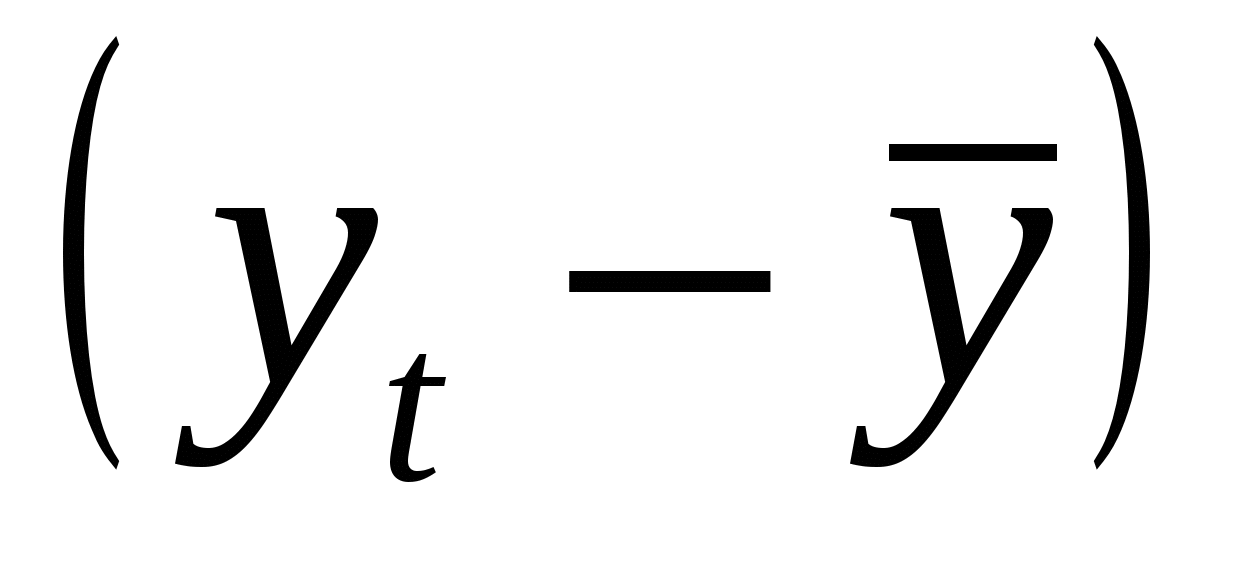
|
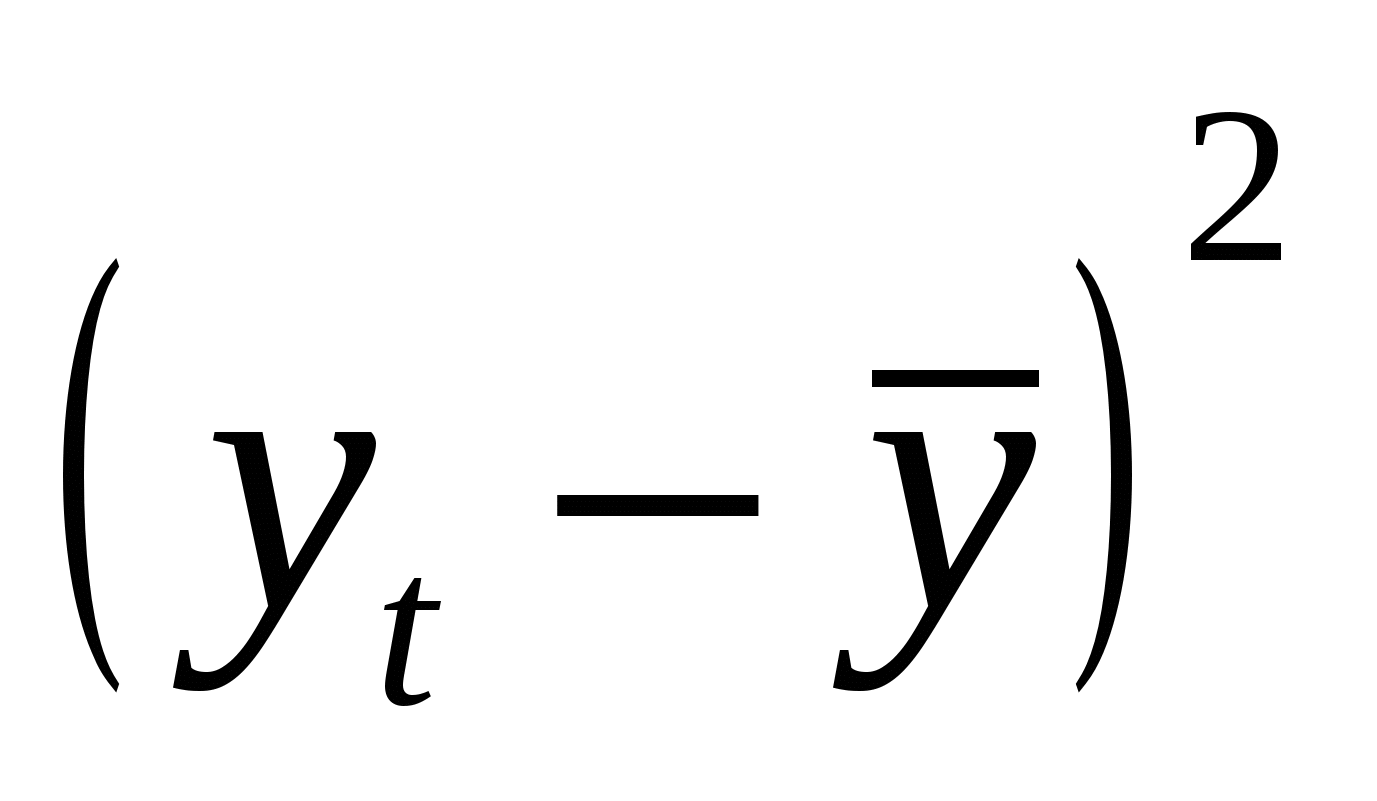
|
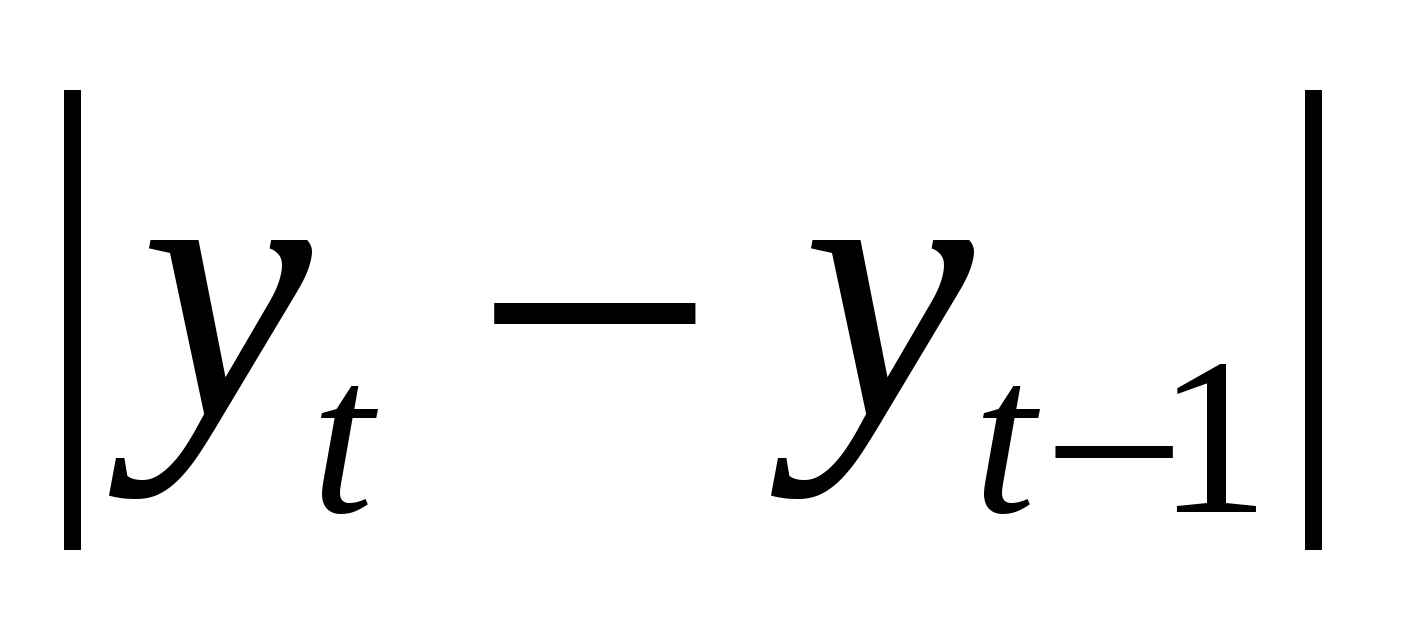
|
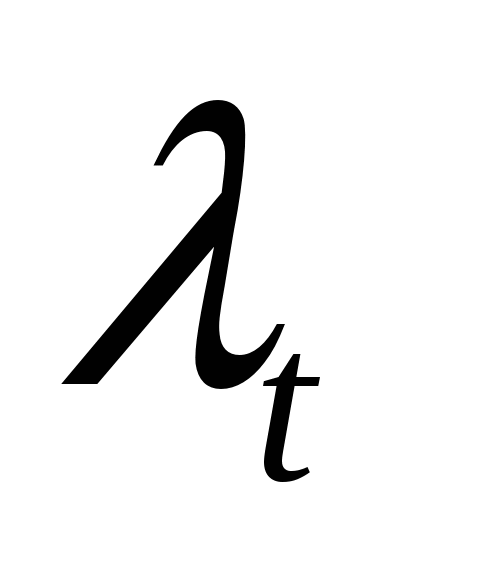
|
|
1
|
5
|
-4
|
16
|
-10,11
|
102,23
|
-
|
-
|
|
2
|
7
|
-3
|
9
|
-8,11
|
65,79
|
2
|
0,28
|
|
3
|
10
|
-2
|
4
|
-5,11
|
26,12
|
3
|
0,42
|
|
4
|
12
|
-1
|
1
|
-3,11
|
9,68
|
2
|
0,28
|
|
5
|
15
|
0
|
0
|
-0,11
|
0,01
|
3
|
0,42
|
|
6
|
18
|
1
|
1
|
2,89
|
8,35
|
3
|
0,42
|
|
7
|
20
|
2
|
4
|
4,89
|
23,90
|
2
|
0,28
|
|
8
|
23
|
3
|
9
|
7,89
|
62,23
|
3
|
0,42
|
|
9
|
26
|
4
|
16
|
10,89
|
118,57
|
3
|
0,42
|
Сумма
|
45
|
136
|
0
|
60
|
0
|
416,89
|
|
|
Среднее
|
5
|
15,11
|
|
|
|
|
|
|
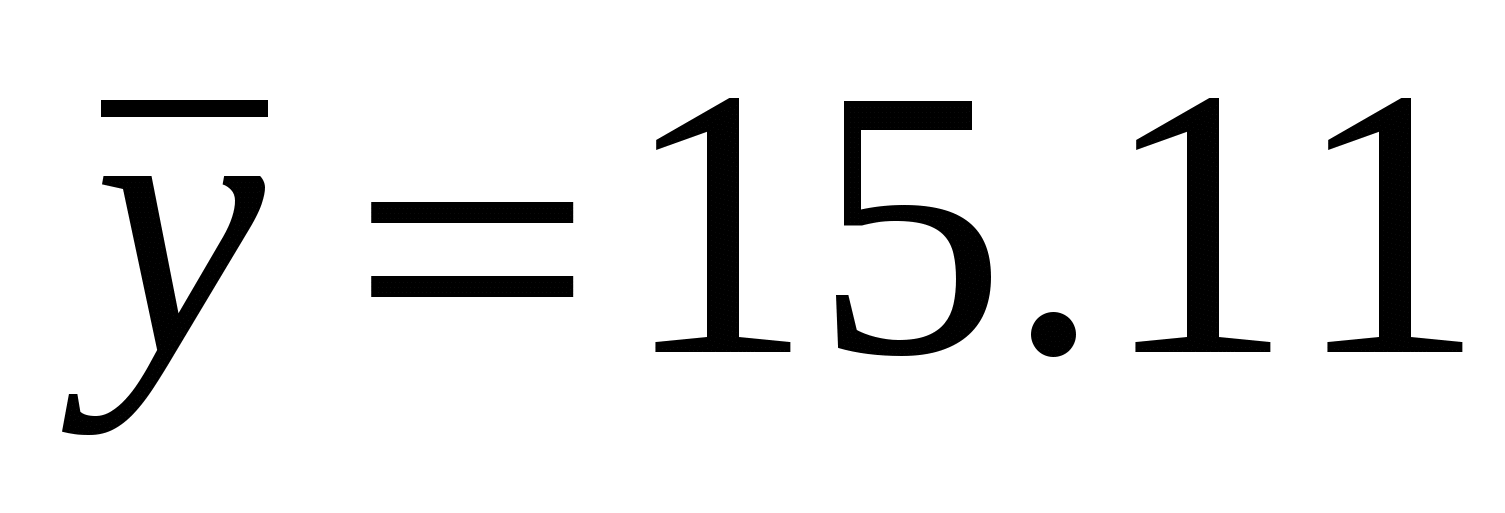 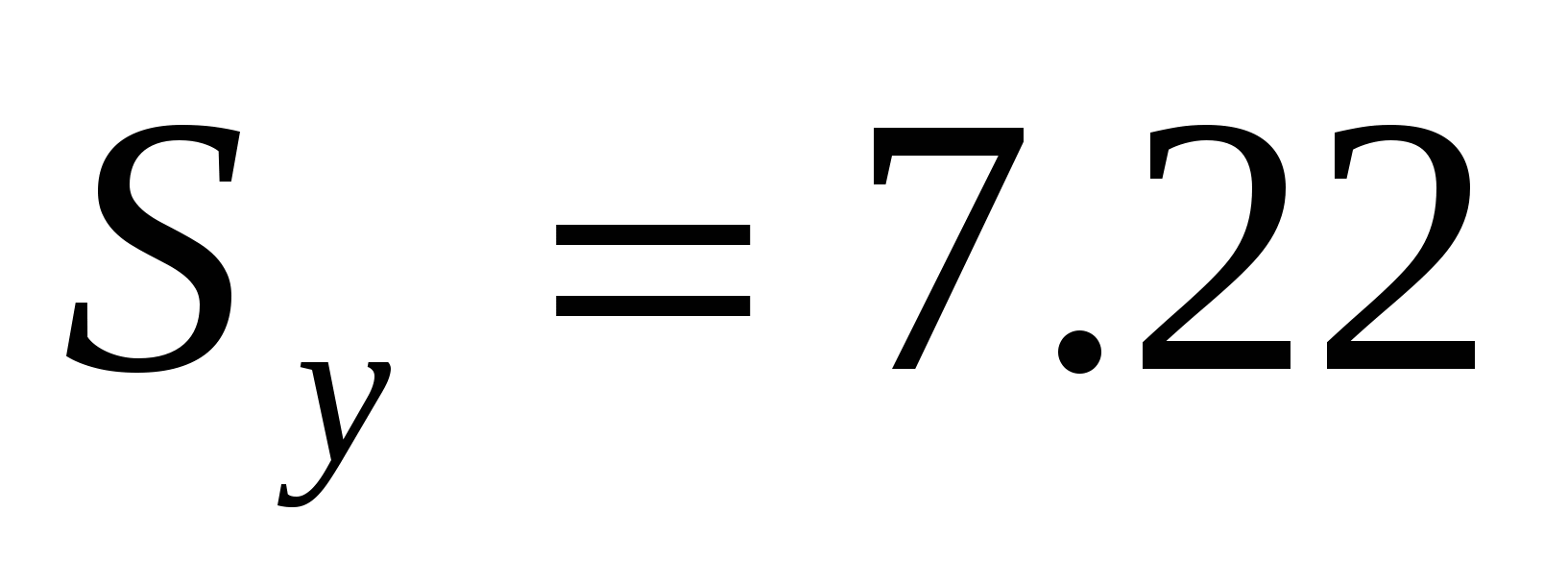 Все полученные значения сравнили с табличными значениями, Все полученные значения сравнили с табличными значениями, 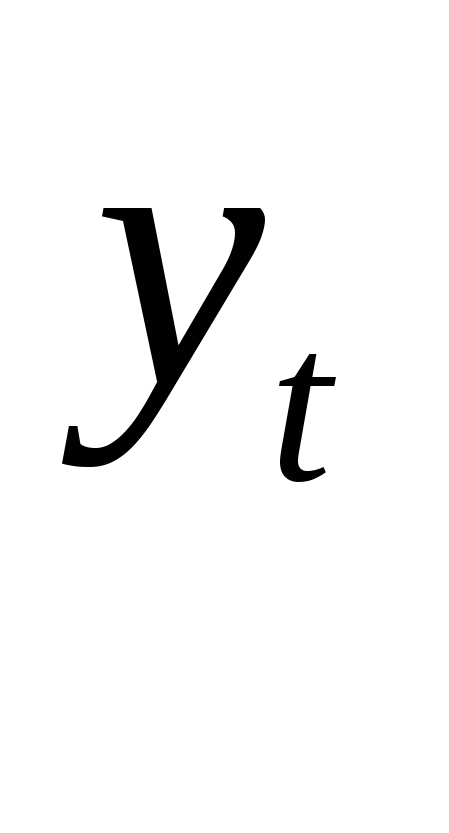 не превышает их, то есть, аномальных наблюдений нет. не превышает их, то есть, аномальных наблюдений нет.
2) Построить линейную модель 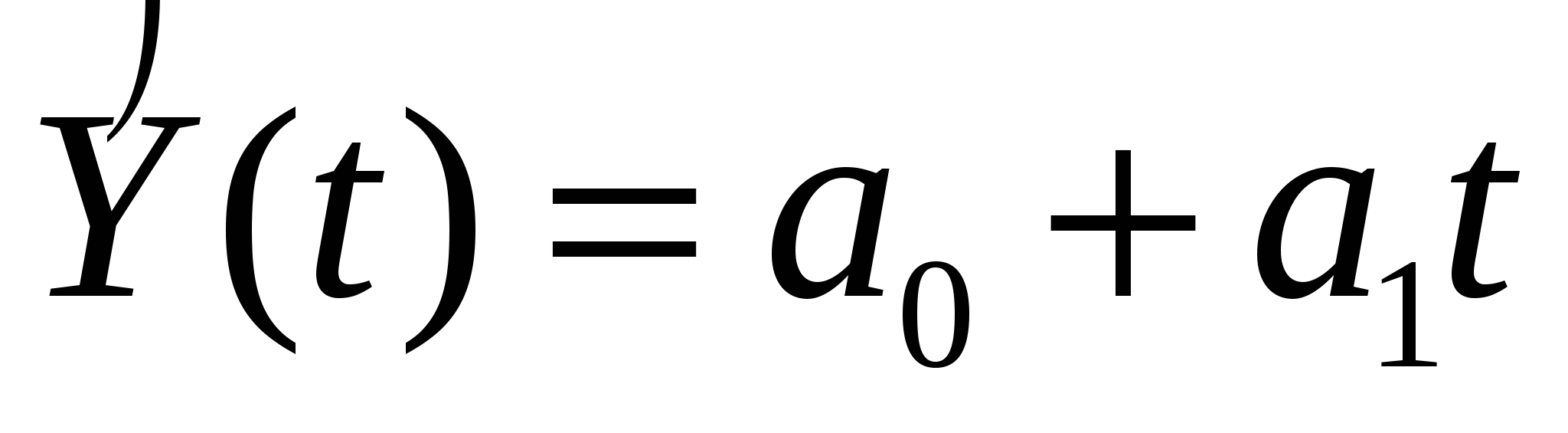 , параметры которой оценить МНК ( , параметры которой оценить МНК (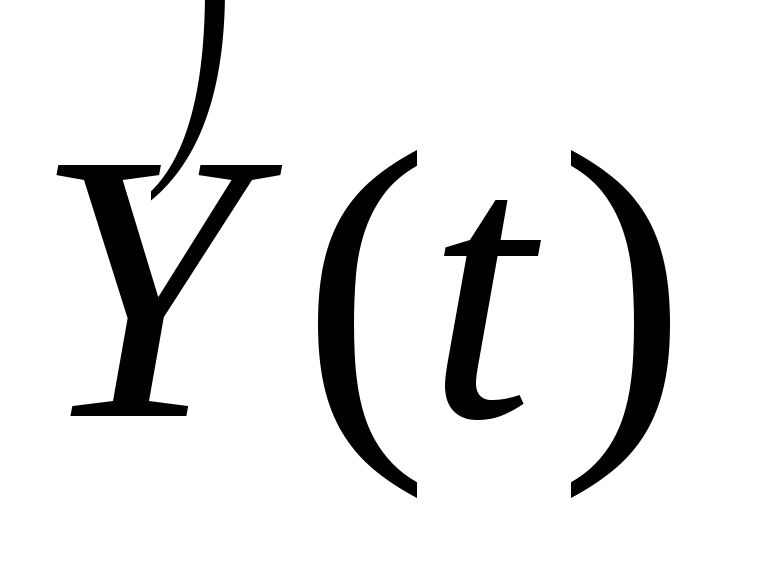 - расчетные, смоделированные значения временного ряда). - расчетные, смоделированные значения временного ряда).
Для этого воспользуемся Анализом данных в Excel (рис. 4.2).
Рис 4.1
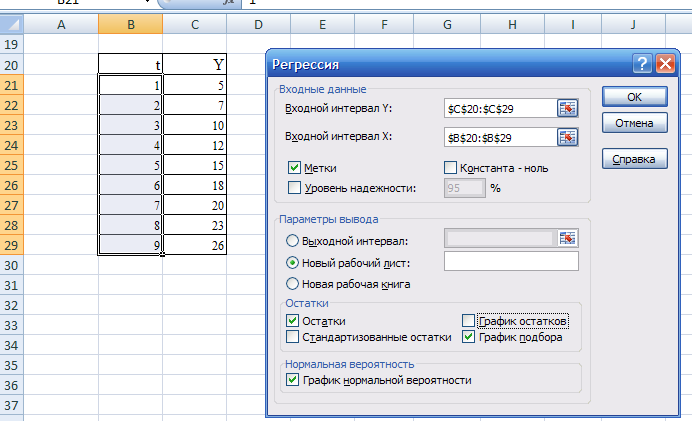
Результат регрессионного анализа содержится в таблице 4.2 и 4.3.
Таблица 4.2
-
|
Коэффициенты
|
Стандартная ошибка
|
t-статистика
|
Y-пересечение а0
|
1,944
|
0,249
|
7,810
|
t a1
|
2,633
|
0,044
|
59,516
|
Во втором столбце табл. 4.3 содержатся коэффициенты уравнения регрессии а0, а1, в третьем столбце – стандартные ошибки коэффициентов уравнения регрессии, а в четвертом – t – статистика, используемая для проверки значимости коэффициентов уравнения регрессии.
Уравнение регрессии зависимости 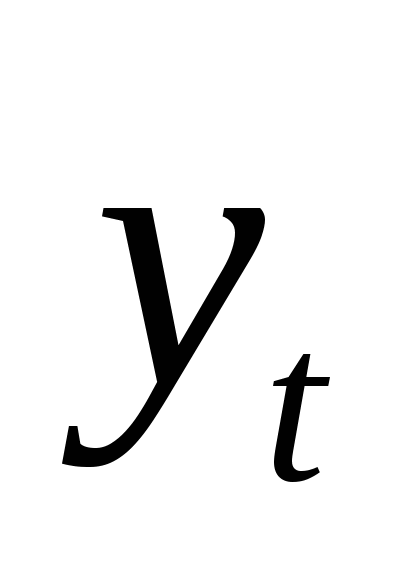 (спрос на кредитные ресурсы) от (спрос на кредитные ресурсы) от 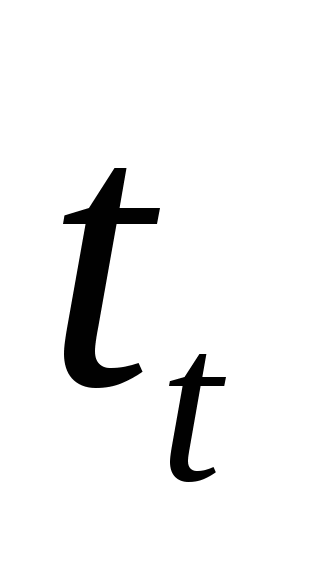 (время) имеет вид (время) имеет вид 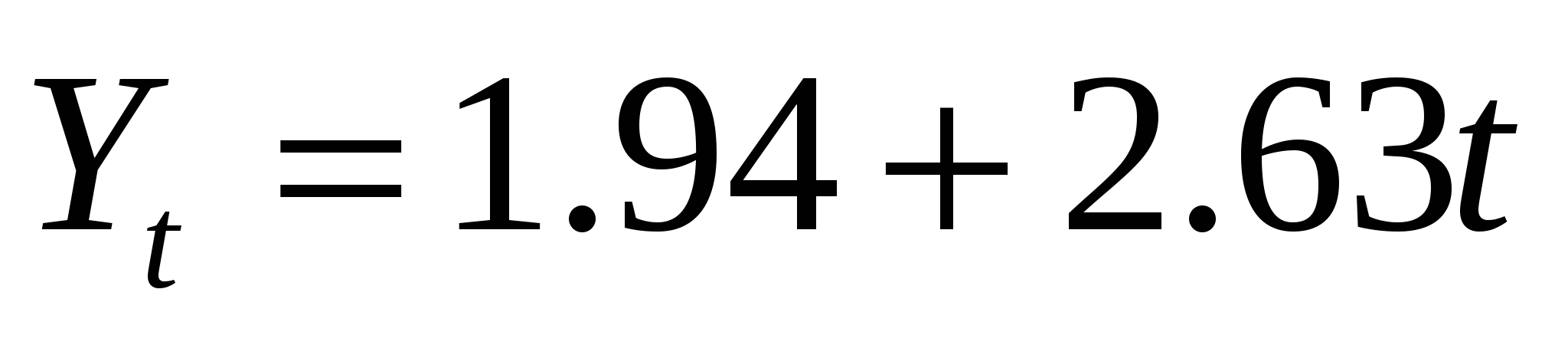 (рис. 4.5). (рис. 4.5).
Таблица 4.3
|
 Скачать 1.03 Mb.
Скачать 1.03 Mb.
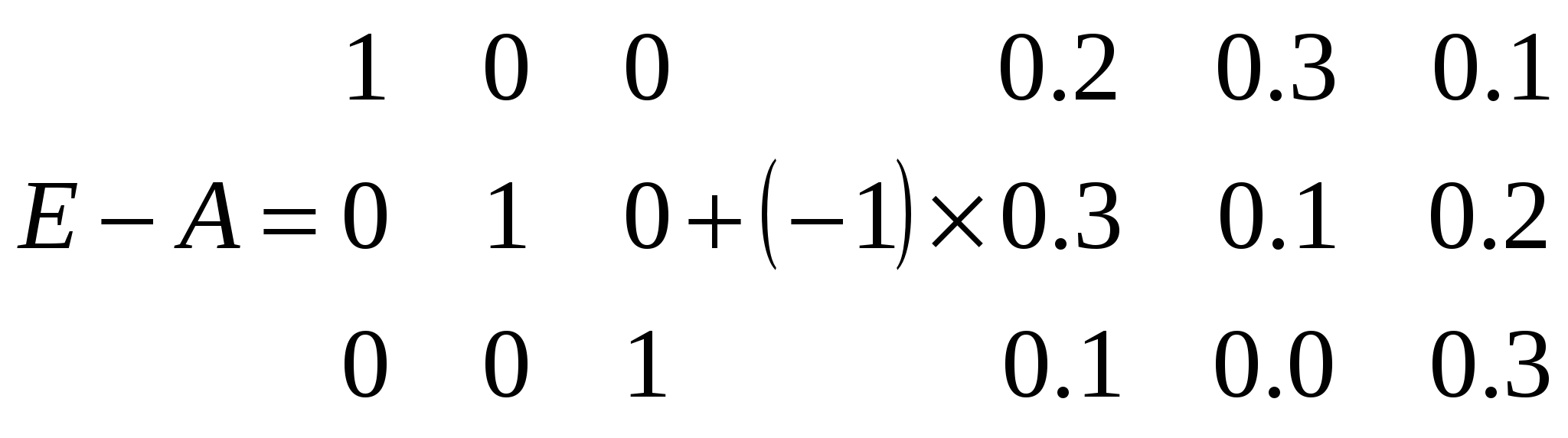




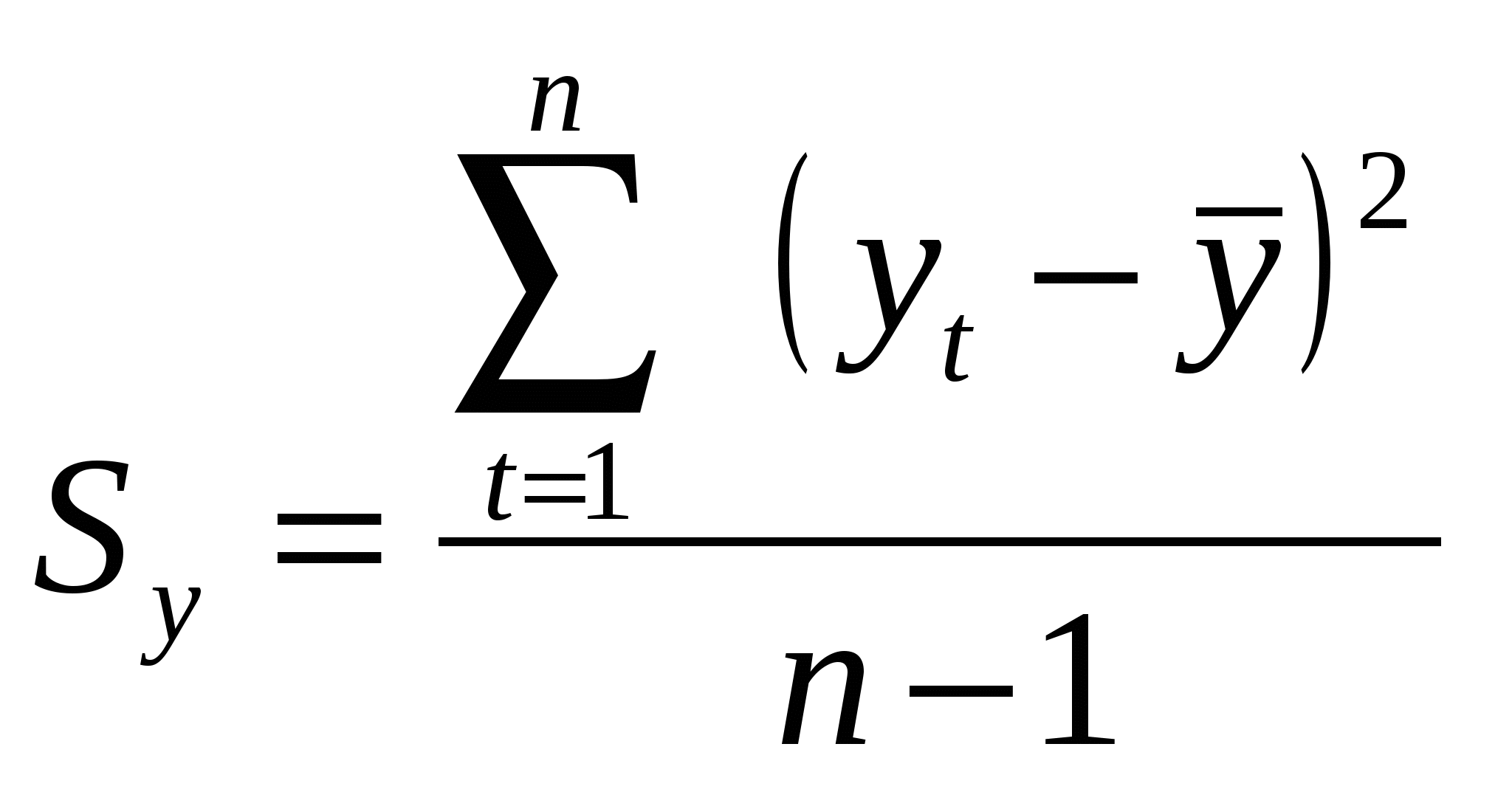 ,
, 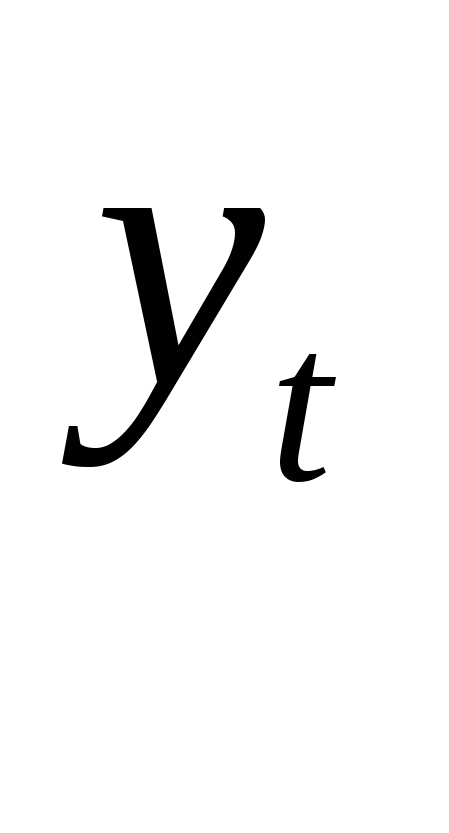 уровня ряда считается аномальным.
уровня ряда считается аномальным.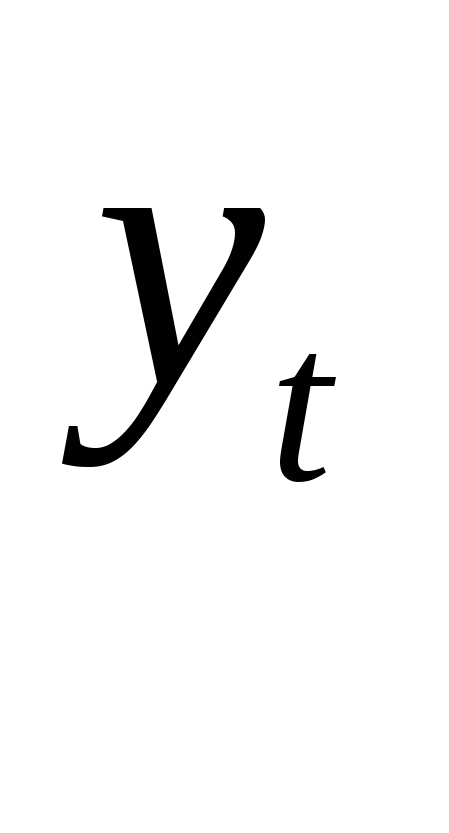 не превышает их, то есть, аномальных наблюдений нет.
не превышает их, то есть, аномальных наблюдений нет.