Примеры решения задач. Задача 1 Решить графическим методом типовую задачу оптимизации
 Скачать 1.03 Mb. Скачать 1.03 Mb.
|
|
Вывод остатков
Рис. 4.4 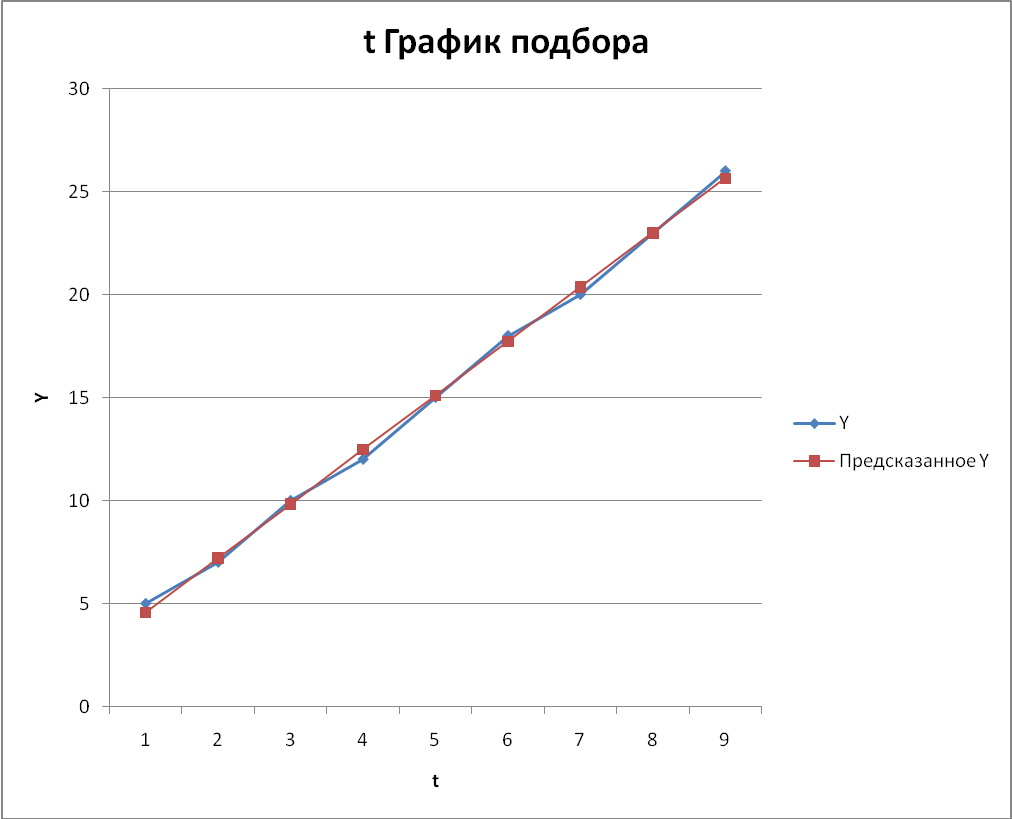 3) Оценить адекватность построенных моделей, используя свойства независимости остаточной компоненты, случайности и соответствия нормальному закону распределения (при использовании R/S-критерия взять табулированные границы 2,7—3,7). Модель является адекватной, если математическое ожидание значений остаточного ряда случайны, независимы и подчинены нормальному закону распределения. 3.1. Проверим независимость (отсутствие автокорреляции) с помощью d – критерия Дарбина – Уотсона по формуле: 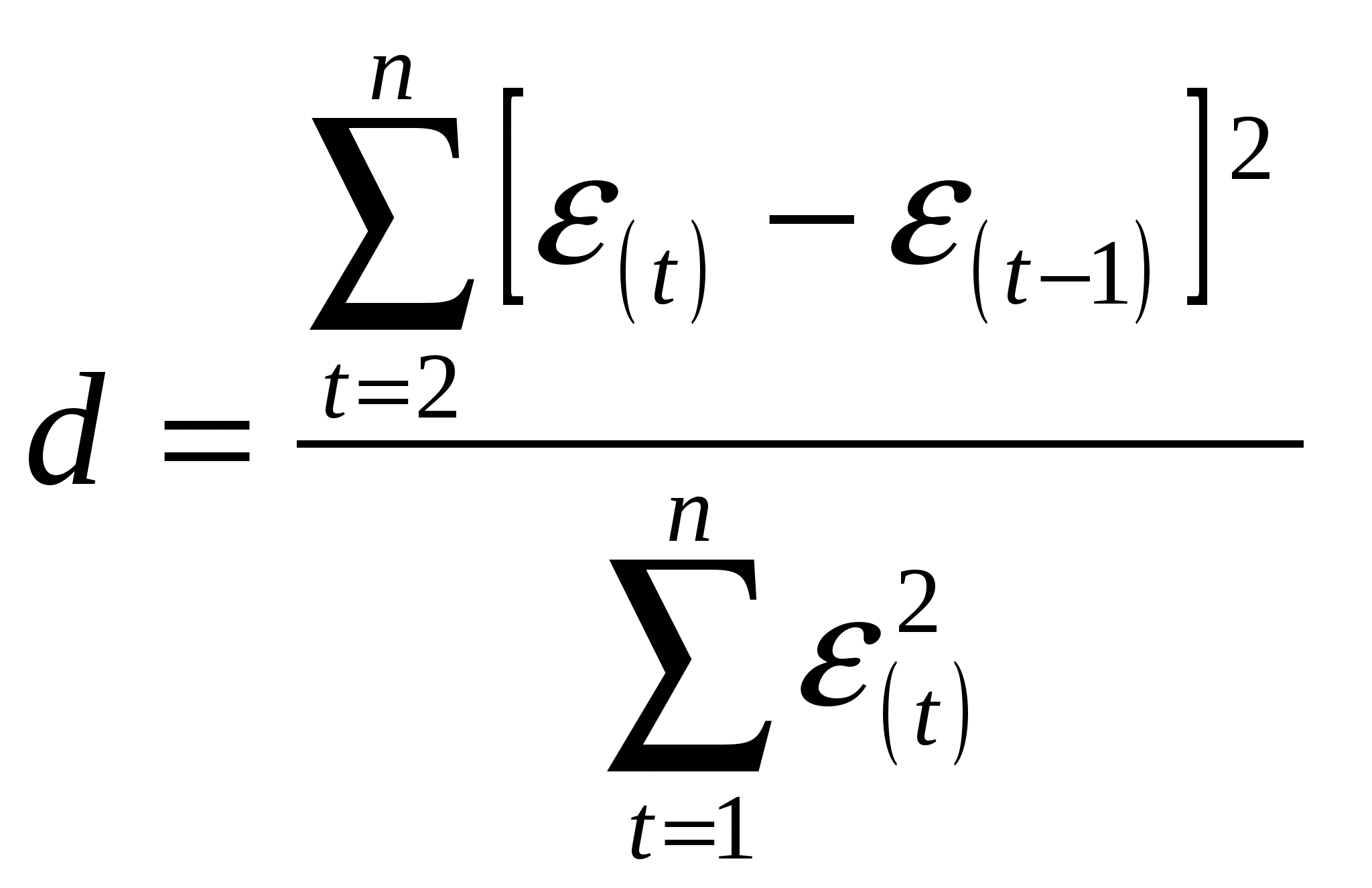 Таблица 4.2
Т.к. расчетное значение d попадает в интервал от 0 до d1, т.е. в интервал от 0 до 1,08, то свойство независимости не выполняется, уровни ряда остатков содержат автокорреляцию. Следовательно, модель по этому критерию неадекватна. 3.2. Проверку случайности уровней ряда остатков проведем на основе критерия поворотных точек. P > [2/3(n-2) – 1, 96 √ (16n-29)/90] Количество поворотных точек равно 6 (рис.4.5). Рис. 4.5  Неравенство выполняется (6 > 2). Следовательно, свойство случайности выполняется. Модель по этому критерию адекватна. 3.3. Соответствие ряда остатков нормальному закону распределения определим при помощи RS – критерия: Расчетное значение попадает в интервал (2,7-3,7), следовательно, выполняется свойство нормальности распределения. Модель по этому критерию адекватна. 3.4. Проверка равенства нулю математического ожидания уровней ряда остатков. В нашем случае В таблице 4.3 собраны данные анализа ряда остатков. Таблица 4.3
4) Оценить точность модели на основе использования средней относительной ошибки аппроксимации. Для оценки точности полученной модели будем использовать показатель относительной ошибки аппроксимации, который вычисляется по формуле: Расчет относительной ошибки аппроксимации Таблица 4.4
Если ошибка, вычисленная по формуле, не превосходит 15%, точность модели считается приемлемой. 5) По построенной модели осуществить прогноз спроса на следующие две недели (доверительный интервал прогноза рассчитать при доверительной вероятности р = 70%). Воспользуемся функцией Excel СТЬЮДРАСПОБР. (рис. 4.10) t = 1,12 Рис. 4.6 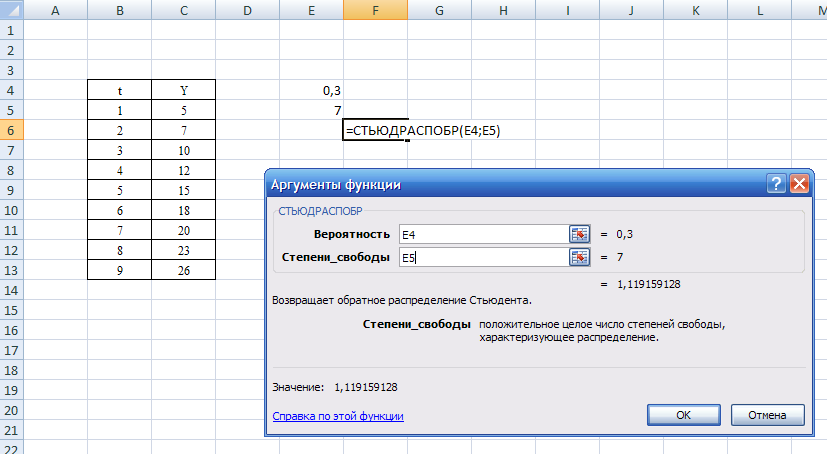 Для построения интервального прогноза рассчитаем доверительный интервал. Примем значение уровня значимости Ширину доверительного интервала вычислим по формуле: 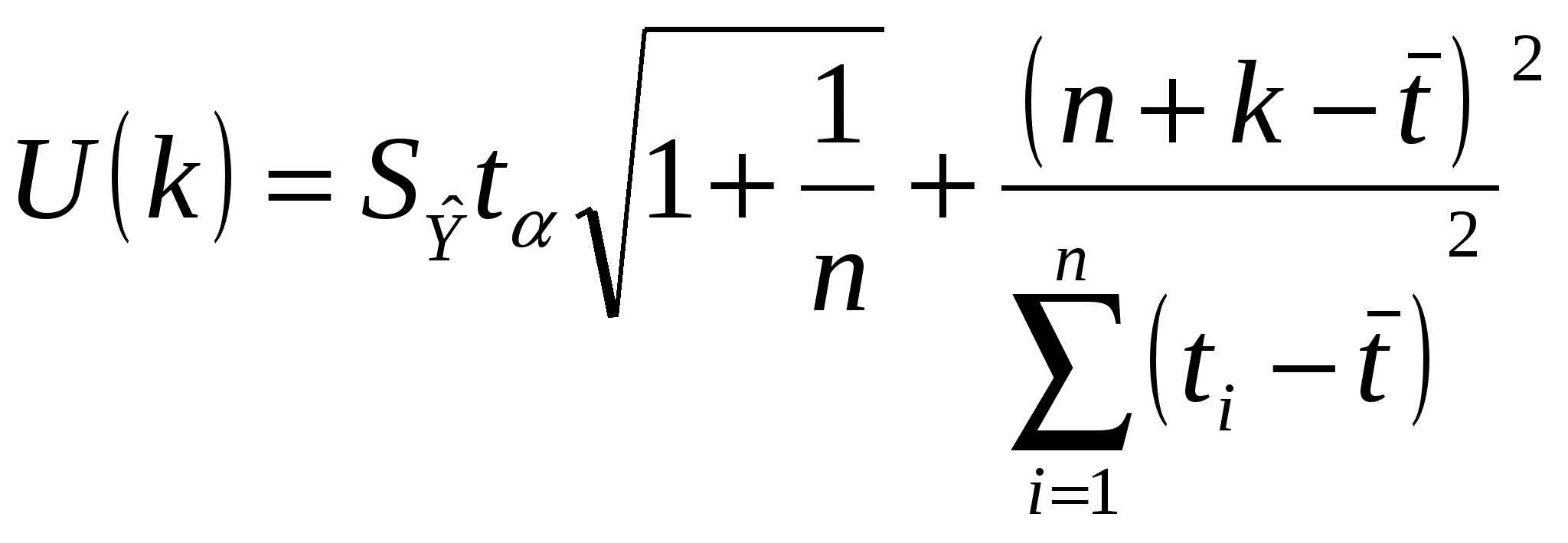 , где , где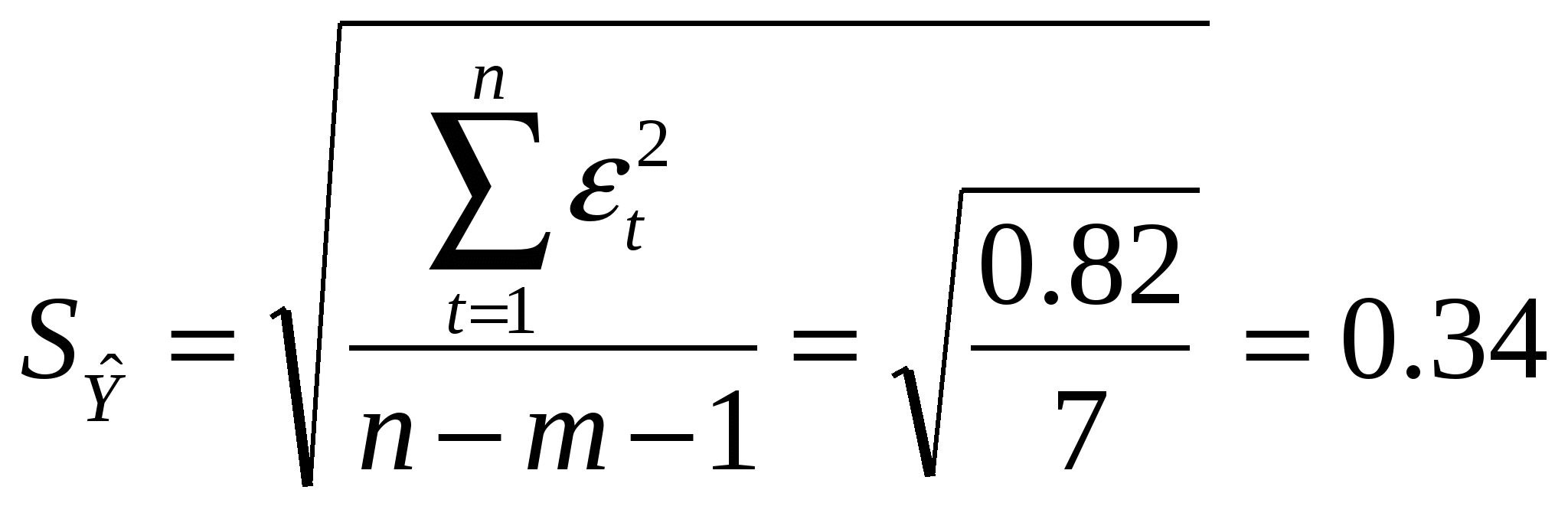 Вычисляем верхнюю и нижнюю границы прогноза (таб. 4.11). Таблица 4.5 Таблица прогноза
6) Фактические значения показателя, результаты моделирования и прогнозирования представить графически. Преобразуем график подбора (рис. 4.5), дополнив его данными прогноза. Рис. 4.7 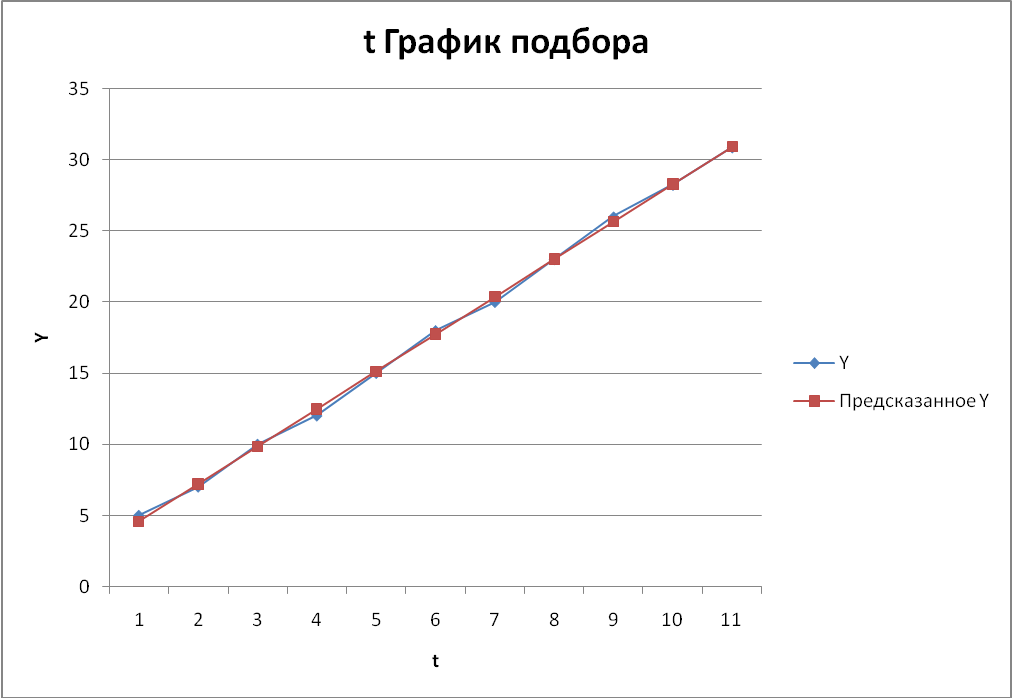 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
