Сопротивление материалов. 4 и 5 задача. Задача 1 Стальной кубик (рис. 1) находится под воздействием сил, создающих плоское напряженное состояние (одно из трех главных напряжений равно нулю). Исходные данные
 Скачать 91.13 Kb. Скачать 91.13 Kb.
|
|
Задача 1 Стальной кубик (рис. 1) находится под воздействием сил, создающих плоское напряженное состояние (одно из трех главных напряжений равно нулю). Исходные данные 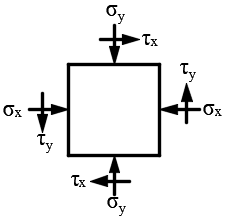 Рис. 1 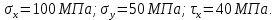 Требуется найти: 1) главные напряжения и направления главных площадок; 2) максимальные касательные напряжения; 3) относительные деформации  4) относительное изменение объема; 5) удельную потенциальную энергию деформации. Решение. 1. Определение главных напряжений и направлений главных площадок Устанавливаем знаки нормальных и касательных напряжений, показанных на рис. 1: 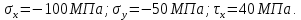 Главные напряжения: 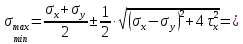 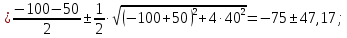 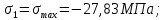 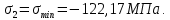 Направление главных площадок: 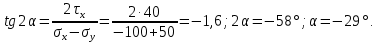 Откладываем угол 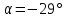 по часовой стрелке и строим главные площадки, на которых откладываем по часовой стрелке и строим главные площадки, на которых откладываем 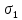 и и 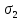 (рис. 2). (рис. 2).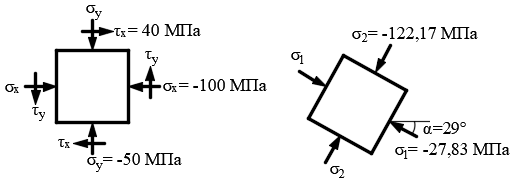 Рис. 2 2. Определение максимальных касательных напряжений Максимальные касательные напряжения: 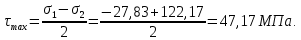 3. Определение относительных деформаций 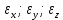 Принимаем коэффициент Пуассона 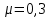 , модуль упругости материала , модуль упругости материала 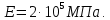 Относительные деформации: 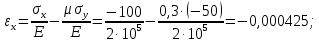 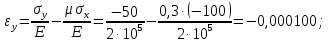 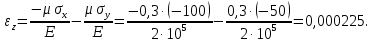 4. Определение относительного изменения объема Относительное изменение объема: 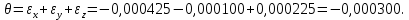 5. Определение удельной потенциальной энергии деформации Удельная потенциальная энергия деформации: 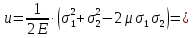 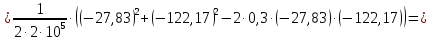 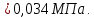 Задача 2 К стальному валу приложены три известных момента: 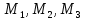 (рис. 3). (рис. 3).Исходные данные 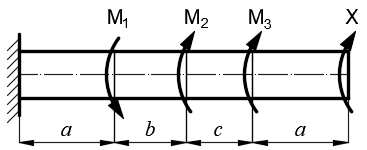 Рис. 3 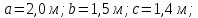 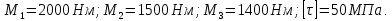 Требуется: 1) установить, при каком значении момента Х угол поворота правого концевого сечения вала равен нулю; 2) для найденного значения Х построить эпюру крутящих моментов; 3) при заданном значении 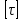 определить диаметр вала из расчета на прочность и округлить его величину до ближайшей большей, соответственно равной: 30, 35, 40, 50, 60, 70, 80, 90, 100 мм; определить диаметр вала из расчета на прочность и округлить его величину до ближайшей большей, соответственно равной: 30, 35, 40, 50, 60, 70, 80, 90, 100 мм;4) построить эпюру углов закручивания; 5) найти наибольший относительный угол закручивания (на 1 метр). Решение. 1. Определение значения момента Х, при котором угол поворота правого концевого сечения вала равен нулю 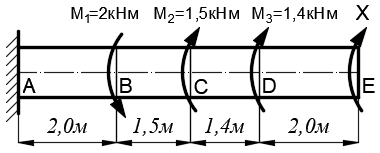 Рис. 4 Вал жестко заделан левым концом А, правый конец E свободный. В сечениях B, C и D приложены известные крутящие моменты. Для определения неизвестного момента Х используем условие равенства нулю угла поворота сечения Е. Угол поворота сечения Е определяется как сумма углов закручивания отдельных участков: 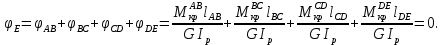 Определяем крутящие моменты для каждого участка: 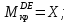 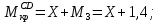 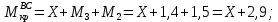 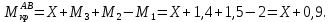 Следовательно: 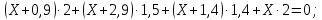 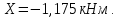 Поскольку значение Х получилось со знаком минус, направление Х выбрано неправильно и его необходимо изменить на противоположное. 2. Построение эпюры крутящих моментов для найденного значения Х 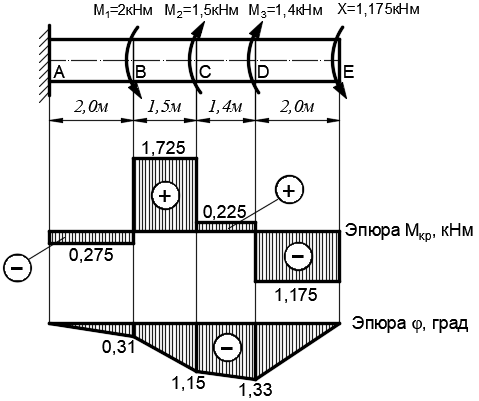 Рис. 5 Определяем крутящие моменты для каждого участка: 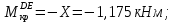 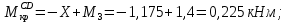 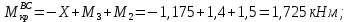 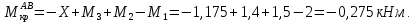 Строим эпюру крутящих моментов  по полученным значениям (рис. 5). по полученным значениям (рис. 5).3. Определение диаметра вала из расчета на прочность Определяем диаметр вала из условия прочности: 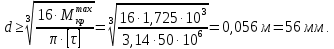 Принимаем 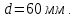 4. Построение эпюры углов закручивания Принимаем модуль сдвига материала 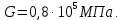 Определяем полярный момент инерции вала: 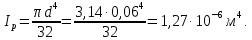 Вычисляем углы закручивания по участкам: 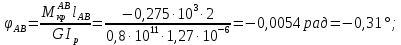 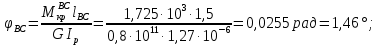 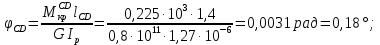 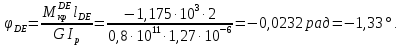 Угол поворота каждого сечения равен сумме углов закручивания соответствующих участков бруса. Суммирование углов начинаем с конца А: 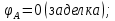 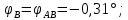 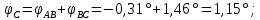 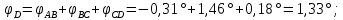 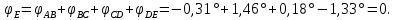 Строим эпюру углов закручивания 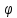 по полученным значениям углов поворота сечений (рис. 5). по полученным значениям углов поворота сечений (рис. 5).5. Определение наибольшего относительного угла закручивания Наибольший относительный угол закручивания: 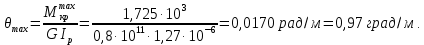 |
