ыфвфывы. Задача 1 Условие задачи
 Скачать 121.36 Kb. Скачать 121.36 Kb.
|
|
ЗАДАЧА 1 Условие задачи. На испытание поставлено N0 изделий. За время t час вышло из строя n(t) штук изделий. За последующий интервал времени Δt вышло из строя n(Δt) изделий. Необходимо вычислить вероятность безотказной работы за время t и t+Δt, частоту отказов и интенсивность отказов на интервале Δt. Исходные данные для решения задачи приведены в табл. 1. Таблица 1
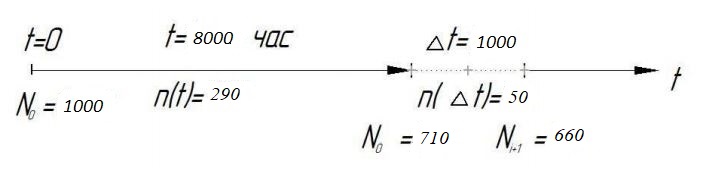 Рис.1. Временной график. Решение. 1. По формуле 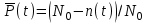 найдем вероятность безотказной работы: найдем вероятность безотказной работы:для tн = 8000 час (начало интервала) 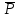 (8000)= (8000)=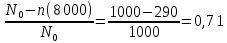 ; ;для tк = 16000 час (конец интервала) 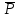 (9000)= (9000)=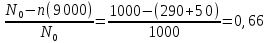 . .Определим среднее число исправно работающих образцов в интервале Δt: 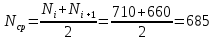 . .Число отказавших изделий за время t = 8500 час п (8500) = N0 - Ncp = 1000 - 685= 315, тогда 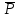 (8500)= (8500)=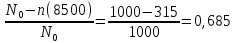 . .2. По формуле 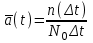 определяем частоту отказа: определяем частоту отказа: 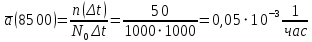 . .3. По формуле 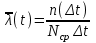 определяем интенсивность отказа определяем интенсивность отказа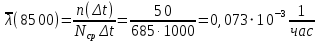 . .Интенсивность отказа можно также определить по формуле 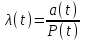 : :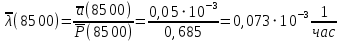 . .ЗАДАЧА 2 Условие задачи. Необходимо выполнить ориентировочный расчет надежности систем, состоящей из N элементов различного типа. Требуется вычислить вероятность безотказной работы системы в течение времени t и среднюю наработку до первого отказа Тср. Расчет следует выполнить по данным о надежности элементов, приведенным в Приложении 1. Исходные данные для решения задачи приведены в табл. 2. Количество силовых трансформаторов Nст соответствует последней цифре учебного шифра (цифра 5 соответствует Nст=1). Таблица 2 Наименование и количество элементов
Решение. Для выполнения ориентировочного расчета надежности составим и заполним табл.3, вычислив величину интенсивности отказов изделия. Значение интенсивностей отказов λi элементов (четвертая графа) выбирается из таблиц Приложения 1. Заполненная табл. 3 приведена ниже. Таблица 3
Найдем интенсивность отказы всей системы по формуле, используя полученные данные в таблице 3, 1/ час, 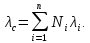 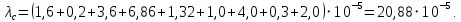 Вероятность безотказной работы 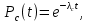 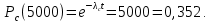 Средняя наработка до первого отказа, час, 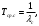 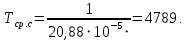 ЗАДАЧА 3 Условие задачи. Схема расчета надежности резервированного устройства для различных вариантов приведена на рис. 4. Интенсивности отказов элементов имеют следующие значения: λ1=1∙10-4 1/час; λ2=2∙10-4 1/час; 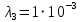 1/час. Предполагается, что последействие отказов элементов отсутствует. Необходимо найти среднюю наработку до первого отказа устройства и вероятность его безотказной работы в течение 100 часов. 1/час. Предполагается, что последействие отказов элементов отсутствует. Необходимо найти среднюю наработку до первого отказа устройства и вероятность его безотказной работы в течение 100 часов. 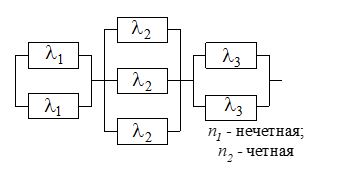 Рис. 4 Решение. Готовой формулы для средней наработки до первого отказа в рассматриваемом случае нет. Поэтому необходимо воспользоваться соотношением 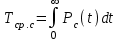 . .Найдем выражение для вероятности безотказной работы Рc(t) устройства. Очевидно, Pc(t)=pI(t)·pII(t)·pIII(t), где 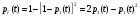 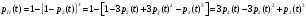 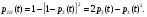 Тогда, подставляя значения pI(t) и pII(t) и pIII(t) в выражение для Рс(t),получим 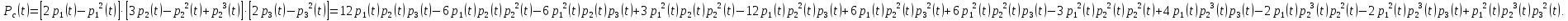 Так как 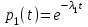 , , 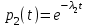 , , 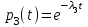 , то , то 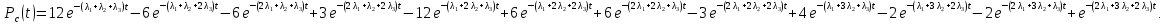 Подставляя в выражение значение интенсивности отказов и времени из условия задачи, получаем 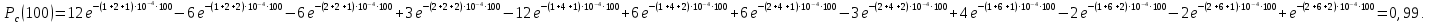 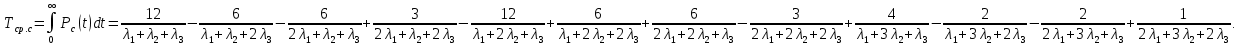 Подставляя в выражение для Тср.с значение интенсивности отказов из условия задачи, получаем 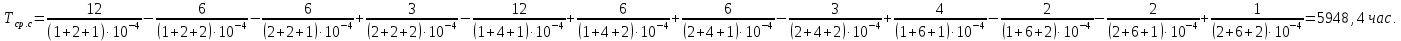 ЗАДАЧА 4 Условия задачи. Составить систему уравнений Колмогорова для графа состояний резервированной системы, изображенного на рис. 5 (в соответствии с вариантом). В данном случае G0 и G1 – работоспособные состояния системы; G2 – неработоспособное состояние; Рi – вероятность нахождения системы в i-ом состоянии; λ – интенсивность отказа; μ – интенсивность восстановления. Рассчитать коэффициент готовности системы (Кг=Р0+Р1), решив полученную систему уравнений. λ=2∙10-4 1/час; μ=1∙10-4 1/час; 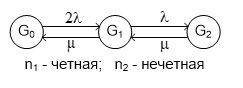 Рис.. Решение. Система составляется по следующим правилам. Производная вероятности состояния равна сумме стольких слагаемых, сколько стрелок связано с этим состоянием. Каждое слагаемое равно произведению интенсивности потока событий, переводящего систему по данной стрелке, на вероятность того состояния, из которого исходит стрелка. Слагаемое имеет знак минус, если стрелка исходит из данного состояния, а знак плюс – если стрелка направлена в данное состояние. Полученная система уравнений называется системой уравнений Колмогорова. Например, для графа состояний, показанного на рис. 5, получим следующую систему дифференциальных уравнений. 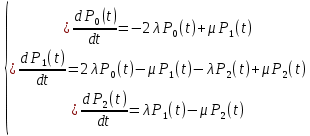 Система решается с помощью преобразований Лапласа или численными методами. При 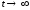 справедлива предельная теорема А.А. Маркова: если все интенсивности потоков событий постоянны, а граф состояний таков, что из каждого состояния можно перейти в каждое другое за конечное число шагов, то предельные вероятности состояний существуют и не зависят от начального состояния системы. В соответствии с этой теоремой при справедлива предельная теорема А.А. Маркова: если все интенсивности потоков событий постоянны, а граф состояний таков, что из каждого состояния можно перейти в каждое другое за конечное число шагов, то предельные вероятности состояний существуют и не зависят от начального состояния системы. В соответствии с этой теоремой при 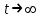 производная производная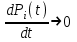 и система дифференциальных уравнений превращается в однородную систему линейных алгебраических уравнений и система дифференциальных уравнений превращается в однородную систему линейных алгебраических уравнений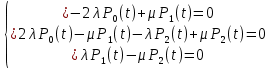 Система дополняется нормировочным уравнением 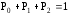 . .Решить систему линейных уравнений можно либо матричным методом, либо методом Крамара, либо методом подстановки. Решим систему уравнений методом подстановки. Выразим из первого уравнения 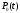 , а из третьего , а из третьего 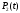 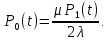 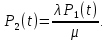 Полученное значение вероятностей подставим в нормировочное уравнение. В результате подстановки получим 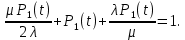 Решив данное уравнение относительно 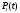 получим получим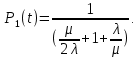 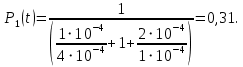 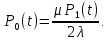 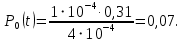 Тогда коэффициент готовности системы будет равен 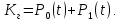 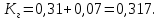 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
