контрольная по эконометрике. КОНТРОЛЬНАЯ по эконометрике. Задача 1 в таблице приведены данные по объемам выпуска

• Название: Задача 1 в таблице приведены данные по объемам выпуска
• Анкор: контрольная по эконометрике
• Дата: 16.03.2022
• Размер: 0.65 Mb.
• Имя файла: КОНТРОЛЬНАЯ по эконометрике.doc
• Тип: Задача; #399534
• страница: 3 из 5

Задача 4

По 10 предприятиям региона изучается зависимость выработки на одного работника у (тыс. руб.) от ввода в действие новых основных фондов х₁ (% от стоимости фондов на конец года) и от удельного веса рабочих высокой квалификации в общей численности рабочих х₂ (%). Требуется:

1. 
   составить сводную таблицу основных статистических характеристик для нескольких массивов данных с помощью инструмента анализа данных Описательная статистика табличного процессора Excel;
   
2. 
   рассчитать матрицу парных коэффициентов корреляции переменных с помощью инструмента анализа данных Корреляция табличного процессора Excel;
   
3. 
   выполнить регрессионный анализ с помощью инструмента анализа данных Регрессия табличного процессора Excel.
   

№ предприятия	Y	X1	Х2
1	6	3,2	11
2	6	3,5	13
3	6	3,7	13
4	7	4	15
5	7	3,8	16
6	7	4,1	16
7	8	5	18
8	8	4,6	19
9	9	5,1	20
10	10	6,4	20

Решение:

1. 
   
   

Y		X1		X2
Среднее	7,4	Среднее	4,34	Среднее	16,1
Стандартная ошибка	0,42687495	Стандартная ошибка	0,301919783	Стандартная ошибка	0,993870101
Медиана	7	Медиана	4,05	Медиана	16
Мода	6	Мода	#Н/Д	Мода	13
Станд. отклонение	1,34989712	Станд. отклонение	0,954754186	Станд. отклонение	3,142893218
Дисперсия выборки	1,82222222	Дисперсия выборки	0,911555556	Дисперсия выборки	9,877777778
Эксцесс	-0,12524433	Эксцесс	1,17460124	Эксцесс	-1,18720838
Асимметричность	0,77241659	Асимметричность	1,107343006	Асимметричность	-0,195416511
Интервал	4	Интервал	3,2	Интервал	9
Минимум	6	Минимум	3,2	Минимум	11
Максимум	10	Максимум	6,4	Максимум	20
Сумма	74	Сумма	43,4	Сумма	161
Счет	10	Счет	10	Счет	10

2.

	Y	X1	X2
Y	1
X1	0,96901737	1
X2	0,93234618	0,883500364	1

3.

ВЫВОД ИТОГОВ
Регрессионная статистика
Множественный R			0,98258316
R-квадрат			0,96546966
Нормированный R-квадрат			0,95560385
Стандартная ошибка			0,28442865
Наблюдения			10
Дисперсионный анализ
		df		SS			MS		F		Значимость F
Регрессия		2		15,83370242			7,916851208		97,86013594		7,65073E-06
Остаток		7		0,566297583			0,080899655
Итого		9		16,4
	Коэффициенты				Стандартная ошибка			t-статистика		P-Значение		Нижние 95%		Верхние 95%
Y-пересечение	0,93506461				0,493952451			1,893025552		0,100228587		-0,23294733		2,103077
X1	0,936164363				0,211989998			4,416077986		0,003095945		0,434887673		1,437441
X2	0,149191432				0,064398732			2,316682758		0,053655978		-0,00308737		0,30147

Столбец Коэффициенты содержит численные значения коэффициентов регрессии:

Y = 0,935 +0,936X1 + 0,149X2

При увеличении введенных в действие основных фондов на 1%, выработка на одного работника увеличится на 0,936 тыс. руб. При увеличении удельного веса рабочих высокой квалификации в общей численности рабочих на 1%, выработка на одного работника увеличится на 0,149 тыс. руб.

Множественный коэффициент детерминации (строка R-квадрат) = 0,965.

Зависимость Y от Х1 т Х2 характеризуется как тесная, в которой 96,5% вариации выработки на одного работника определяется вариацией учтенных в модели факторов: ввода в действие новых основных фондов и удельного веса рабочих высокой квалификации в общей численности рабочих.
Задача 5

Динамика выпуска продукции Финляндии характеризуется данными (млн.долл.), представленными в таблице. Требуется:

1. 
   провести расчет параметров линейного и экспоненциального трендов с использованием статистических функций ЛИНЕЙН и ЛГРФПРИБЛ табличного процессора Excel;
   
2. 
   построить графики ряда динамики и трендов с помощью Мастера диаграмм табличного процессора Excel;
   
3. 
   выбрать наилучший вид тренда на основании графического изображения и значения коэффициента детерминации .
   

Год	Выпуск продукции
1981	14000
1982	13091
1983	12522
1984	13474
1985	13616
1986	16354
1987	20037
1988	21745
1989	23299
1990	26572

Решение:

1. При расчете параметров линейного тренда появится следующая таблица:

1534,21818	-3028719,2
231,150561	458949,9194
0,84631314	2099,529235
44,0538984	8
194190598	35264184,07

Для вычисления параметров экспоненциальной кривой y=^x появится следующая таблица:

1,08812847	2,50268E-69
0,01240261	24,62540817
0,85286895	0,112652301
46,3732941	8
0,58850218	0,101524327

2. 
   Построим графики ряда динамики и трендов: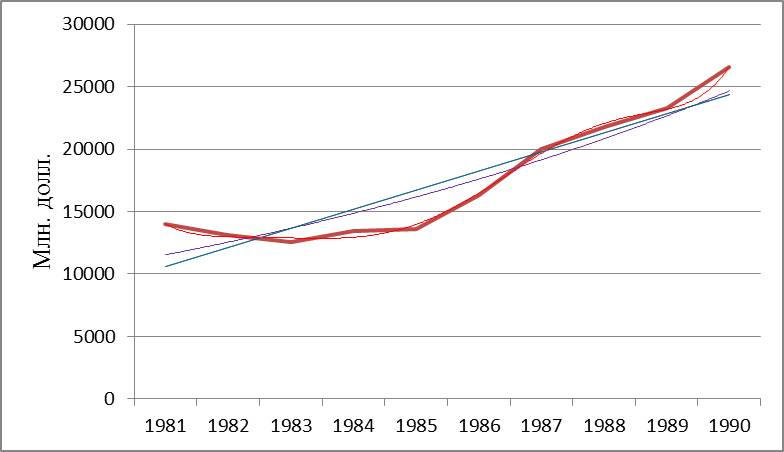
   

3. 
   Сравним значения R² по разным уравнениям трендов:
   

- полиномиальный 6-й степени –R²=0,9964;

- экспоненциальный – R²=0,852;

- линейный – R²=0,8463;

- степенной – R²=0,5963;

- логарифмический – R²=0,5824.

Исходные данные лучше всего описывает полином 6-й степени. Следовательно, в рассматриваемом примере для расчета прогнозных значений следует использовать полиномиальное уравнение.