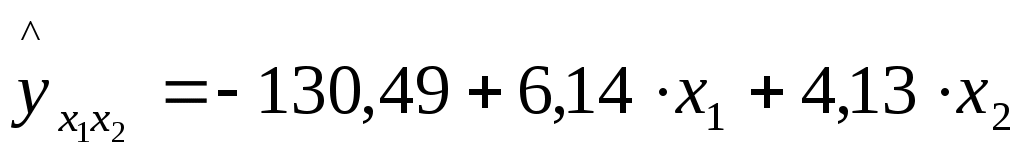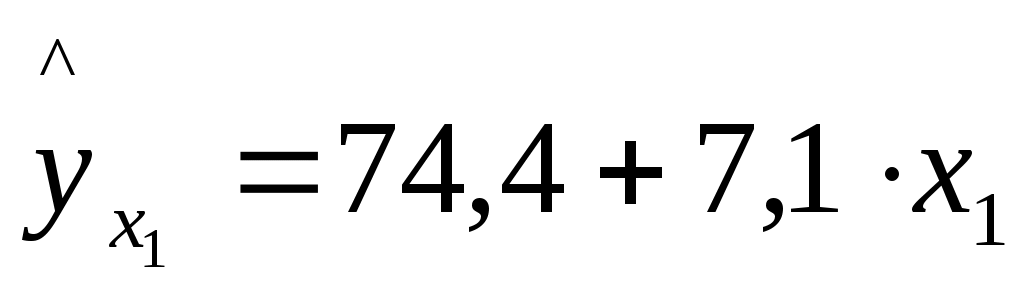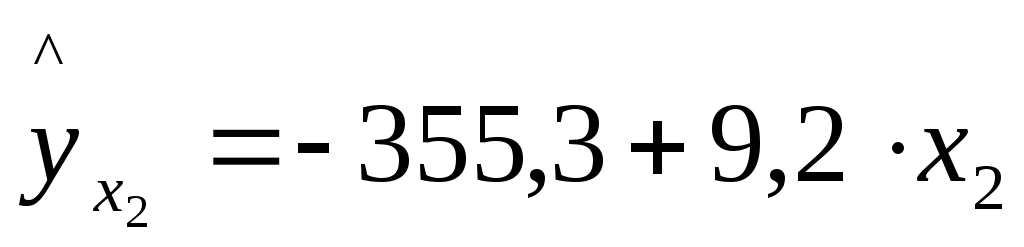контрольная по эконометрике. КОНТРОЛЬНАЯ по эконометрике. Задача 1 в таблице приведены данные по объемам выпуска
 Скачать 0.65 Mb.
|
|
Задача 6 1) Оценить следующую структурную модель на идентификацию; 2) исходя из приведенной формы модели уравнений найти структурные коэффициенты модели Структурная модель  , , . Приведенная форма  , , ,Решение: Модель имеет три эндогенные (y1, y2, y3) и три экзогенные (x1, x2, x3) переменные. Проверим каждое уравнение системы на необходимое (H) и достаточное (Д) условия идентификации. Первое уравнение: Н: эндогенных переменных – 2 (y1, y2), отсутствующих экзогенных – 1 (x3). Выполняется необходимое равенство: 2=1+1, следовательно, уравнение точно идентифицируемо. Д: в первом уравнении отсутствуют y3 и x3. Построим матрицу из коэффициентов при них в других уравнениях системы:
 .Определитель матрицы не равен 0, ранг матрицы равен 2; следовательно, выполняется достаточное условие идентификации, и первое уравнение точно идентифицируемо. Второе уравнение: Н: эндогенных переменных – 3 (y1, y2, y3), отсутствующих экзогенных – 2 (x1, x3). Выполняется необходимое равенство: 3=2+1, следовательно, уравнение точно идентифицируемо. Д: во втором уравнении отсутствуют x1 и x3. Построим матрицу из коэффициентов при них в других уравнениях системы:
 .Определитель матрицы не равен 0, ранг матрицы равен 2; следовательно, выполняется достаточное условие идентификации, и второе уравнение точно идентифицируемо. Третье уравнение: Н: эндогенных переменных – 2 (y2, y3), отсутствующих экзогенных – 1 (x2). Выполняется необходимое равенство: 2=1+1, следовательно, уравнение точно идентифицируемо. Д: в третьем уравнении отсутствуют y1 и x2. Построим матрицу из коэффициентов при них в других уравнениях системы:
 .Определитель матрицы не равен 0, ранг матрицы равен 2; следовательно, выполняется достаточное условие идентификации, и третье уравнение точно идентифицируемо. Следовательно, исследуемая система точно идентифицируема и может быть решена косвенным методом наименьших квадратов. Вычислим структурные коэффициенты модели: из второго уравнения приведенной формы выразим x3 (так как его нет в первом уравнении структурной формы):  .Данное выражение содержит переменные y2, x1 и x2, которые нужны для первого уравнения структурной формы модели (СФМ). Подставим полученное выражение x3в первое уравнение приведенной формы модели (ПФМ):   – первое уравнение СФМ;во втором уравнении СФМ нет переменных x1 и x3. Структурные параметры второго уравнения СФМ можно будет определить в два этапа: Первый этап: выразим x1 из первого уравнения ПФМ:  .Подстановка данного выражения во второе уравнение ПФМ не решило бы задачу до конца, так как в выражении присутствует x3, которого нет в СФМ. Выразим x3 из третьего уравнения ПФМ:  .Подставим его в выражение x1:   .Второй этап: аналогично, чтобы выразить x3 через искомые y1, y3 и x2, заменим в выражении x3 значение x1 на полученное из первого уравнения ПФМ:  .Следовательно,  .Подставим полученные x1 и x3 во второе уравнение ПФМ:   – второе уравнение СФМ.из второго уравнения ПФМ выразим x1:  .Подставим полученное выражение в третье уравнение ПФМ:   – третье уравнение СФМ.Таким образом, СФМ примет вид: , , .Задача 7 По 30 территориям России имеются данные, представленные таблицей. Требуется: Построить уравнение множественной регрессии в стандартизованной и естественной форме; рассчитать частные коэффициенты эластичности, сравнить их с 1 и 2, пояснить различия между ними. Рассчитать линейные коэффициенты частной корреляции и коэффициент множественной корреляции, сравнить их с линейными коэффициентами парной корреляции, пояснить различия между ними. Рассчитать общий и частные F-критерии Фишера. Таблица 3.1
Решение: Линейное уравнение множественной регрессии y от x1 и x2 имеет вид: y=a+b1x1+b2x2. Для расчета его параметров применим метод стандартизации переменных и построим искомое уравнение в стандартизованном масштабе:  .Расчет -коэффициентов выполним по формулам: 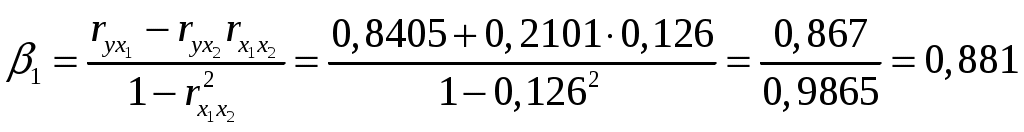 ; 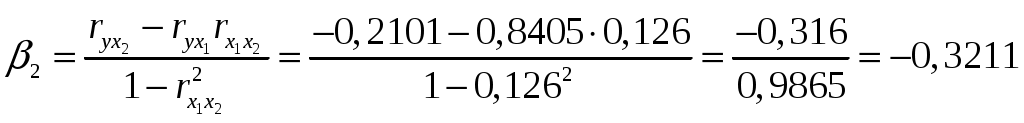.Получим уравнение  .Для построения уравнения в естественной форме рассчитаем b1 и b2, используя формулы для перехода от i к bi:  ;  ;  ;  .Значение a определим из соотношения  , тогда получим  .Для характеристики относительной силы влияния x1 и x2 на y рассчитаем средние коэффициенты эластичности:  ;  ;  .С увеличением средней заработной платы x1 на 1% от ее среднего уровня средний душевой доход y возрастает на 1,12% от своего среднего уровня; при повышении среднего возраста безработного x2 на 1% среднедушевой доход y снижается на 2,43% от своего среднего уровня. Очевидно, что сила влияния средней заработной платы x1 на средний душевой доход y оказалась большей, чем сила влияния среднего возраста безработного x2. К аналогичным выводам о силе связи приходим при сравнении модулей значений 1 и 2:  .Различия в силе влияния фактора на результат, полученные при сравнении  и j, объясняются тем, что коэффициент эластичности исходит из соотношения средних отклонений , а -коэффициент – из соотношения средних квадратических отклонений :Линейные коэффициенты частной корреляции здесь рассчитываются по рекуррентной формуле: 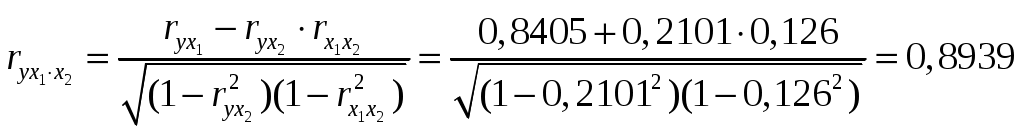 ; ;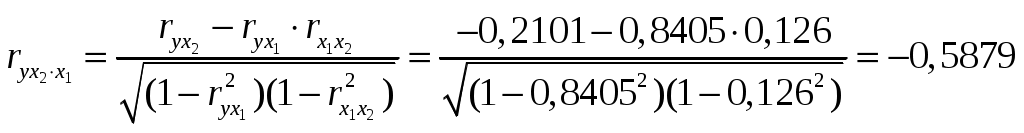 .Если сравнить значения коэффициентов парной и частной корреляции, то приходим к выводу, что из-за слабой межфакторной связи  коэффициенты парной и частной корреляции отличаются незначительно: выводы о тесноте и направлении связи на основе коэффициентов парной и частной корреляции совпадают:  ;  ;  ;  ;  ;  .Расчет линейного коэффициента множественной корреляции выполним с использованием коэффициентов  и j: Зависимость y от x1 и x2 характеризуется как тесная, в которой 80,8% вариации среднего душевого дохода определяются вариацией учтенных в модели факторов: средней заработной платы и среднего возраста безработного. Прочие факторы, не включенные в модель, составляют соответственно 19,2% от общей вариации y. Общий F-критерий проверяет гипотезу H0о статистической значимости уравнения регрессии и показателя тесноты связи (R2=0): 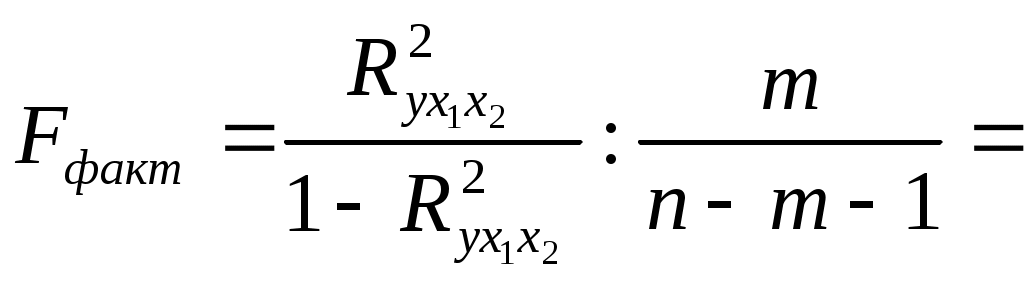 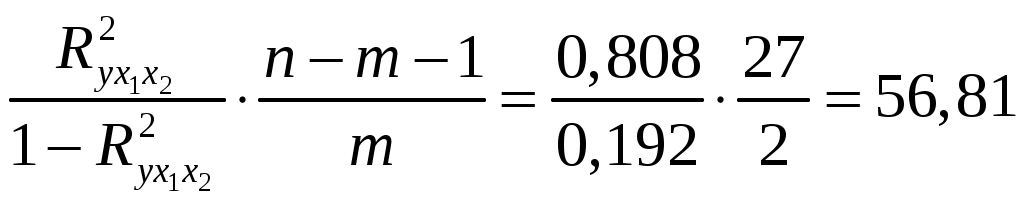 ; Fтабл=3,4; =0,05. Сравнивая Fтабл и Fфакт, приходим к выводу о необходимости отклонить гипотезу H0, так как Fтабл=3,4<Fфакт=56,81. С вероятностью 1 – = 0,95 делаем заключение о статистической значимости уравнения в целом и показателя тесноты связи  , которые сформировались под неслучайным воздействием факторов x1 и x2 .Частные F-критерии – 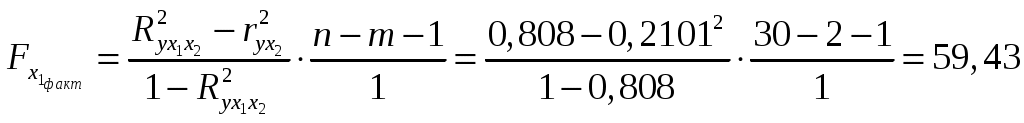 и  оценивают статистическую значимость присутствия факторов x1 и x2 в уравнении множественной регрессии, оценивают целесообразность включения в уравнение одного фактора после другого фактора, т.е. оценивает целесообразность включения в уравнение фактора x1 после того, как в него был включен фактор x2. Соответственно указывает на целесообразность включения в модель фактора x2 после фактора x1:  ;Fтабл=4,21; =0,05. Сравнивая Fтабл и Fфакт, приходим к выводу о целесообразности включения в модель фактора x1 после фактора x2, так как  . Гипотезу H0 о несущественности прироста  за счет включения дополнительного фактора x1 отклоняем и приходим к выводу о статистически подтвержденной целесообразности включения фактора x1 после фактора.Целесообразность включения в модель фактора x2 после фактора x1 проверяет : .Высокое значение  свидетельствует о статистической значимости прироста  за счет включения в модель фактора x2 после фактора x1. Следовательно, подтверждается нулевая гипотеза H0 о целесообразности включения в модель фактора x2 (средний возраст безработного). Это означает, что парная регрессионная модель зависимости среднего дохода от средней заработной платы является недостаточно статистически значимой, надежной и что есть необходимость улучшать ее, включая дополнительный фактор x2 (средний возраст безработного).Задача 8 По территориям России изучаются следующие данные, представленные в таблице: зависимость среднегодового душевого дохода y (тыс. руб.) от доли занятых тяжелым физическим трудом в общей численности занятых x1(%) и от доли экономики активного населения в численности всего населения x2(%). Таблица 3.2
Требуется: Составить таблицу дисперсионного анализа для проверки при уровне значимости =0,05 статистической значимости уравнения множественной регрессии и его показателя тесноты связи. С помощью частных F-критериев Фишера оценить, насколько целесообразно включение в уравнение множественной регрессии фактораx1 после фактора x2и насколько целесообразно включение x2послеx1. Оценить с помощью t-критерия Стьюдента статистическую значимость коэффициентов при переменных x1иx2 множественного уравнения регрессии. Решение: Задача дисперсионного анализа состоит в проверке нулевой гипотезы H0о статистической незначимости уравнения регрессии в целом и показателя тесноты связи. Анализ выполняется при сравнении фактического и табличного (критического) значений F-критерия Фишера Fтабли Fфакт. Fфакт определяется из соотношения значений факторной и остаточной дисперсий, рассчитанных на одну степень свободы: 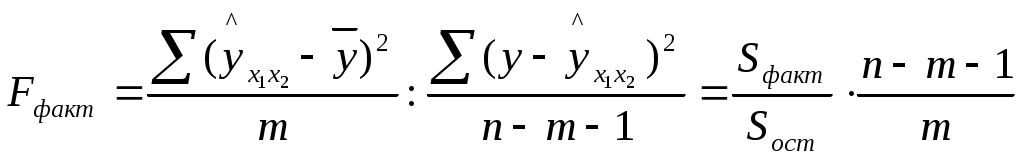 ,где n – число единиц совокупности; m – число факторов в уравнении линейной регрессии;  – фактическое значение результативного признака; – расчетное значение результативного признака.Результаты дисперсионного анализа представлены в табл.:
 ; ; ; .Сравнивая Fтабли Fфакт, приходим к выводу о необходимости отклонить гипотезуH0 и сделать вывод о статистической значимости уравнения регрессии в целом и значения  , так как они статистически надежны и сформировались под систематическим действием неслучайных причин. Вероятность того, что допускаются ошибки при отклонении нулевой гипотезы, не превышает 5%, и это является достаточно малой величиной.Частный F-критерий Фишера оценивает статистическую целесообразность включения фактора x1 в модель после того, как в нее включен фактор x2. Частный F-критерий Фишера строится как отношение прироста факторной дисперсии за счет дополнительно включенного фактора (на одну степень свободы) к остаточной дисперсии (на одну степень свободы), подсчитанной по модели с включенными факторамиx1 и x2: 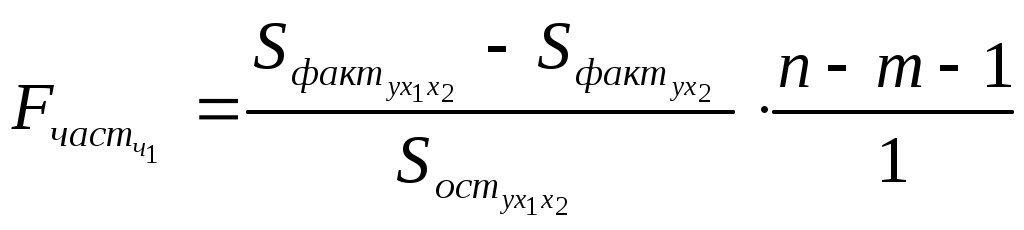 .Результаты дисперсионного анализа представлены в табл.:
; ; ;  ;  .Включение фактора x1после фактораx2 оказалось статистически значимым и оправданным: прирост факторной дисперсии (в расчете на одну степень свободы) оказался существенным, т.е. следствием дополнительного включения в модель систематически действующего фактора x1, так как  .Аналогично проверим целесообразность включения в модель дополнительного фактора x2после включенного ранее фактора x1. Расчет выполним с использованием показателей тесноты связи 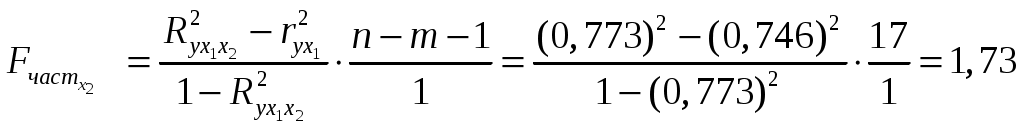и : .В силу того что  , приходим к выводу, что включение x2после x1оказалось бесполезным: прирост факторной дисперсии в расчете на одну степень свободы был несуществен, статистически незначим, т.е. влияние x2не является устойчивым, систематическим. Вполне возможно было ограничиться построением линейного уравнения парной регрессии y от x1.Оценка с помощью t-критерия Стьюдента значимости коэффициентов b1 и b2связана с сопоставлением их значений с величиной их случайных ошибок:  и  . Расчет значений случайных ошибок достаточно сложен и трудоемок. Поэтому предлагается более простой способ: расчет значения t-критерия Стьюдента для коэффициентов регрессии линейного уравнения как квадратного корня из соответствующего частного F-критерия Фишера: ;  .Табличные (критические) значения t-критерия Стьюдента зависят от принятого уровня значимости (обычно это 0,1; 0,05 или 0,01) и от числа степеней свободы (n-m-1), где n – число единиц совокупности, m – число факторов в уравнении. В нашем примере при =0,05; df=20-3=17; tтабл=2,10. Сравнивая tтабл и tфакт, приходим к выводу, что так как  , коэффициент регрессии b1 является статистически значимым, надежным, на него можно опираться в анализе и в прогнозе. Так как  , приходим к заключению, что величинаb2 является статистически незначимой, ненадежной в силу того, что она формируется преимущественно под воздействием случайных факторов. Еще раз подтверждается статистическая значимость влияния x1 (доли занятых тяжелым физическим трудом) на y(среднедушевой доход) и ненадежность, незначимость влиянияx2 (доли экономически активного населения в численности всего населения). | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
