контрольная по эконометрике. КОНТРОЛЬНАЯ по эконометрике. Задача 1 в таблице приведены данные по объемам выпуска

• Название: Задача 1 в таблице приведены данные по объемам выпуска
• Анкор: контрольная по эконометрике
• Дата: 16.03.2022
• Размер: 0.65 Mb.
• Имя файла: КОНТРОЛЬНАЯ по эконометрике.doc
• Тип: Задача; #399534
• страница: 5 из 5

Задача 9

По данным за 18 месяцев построено уравнение регрессии зависимости прибыли предприятия y(млн. руб.) от цен на сырье x₁ (тыс. руб. за 1т) и производительности труда x₂ (ед. продукции на 1 работника) 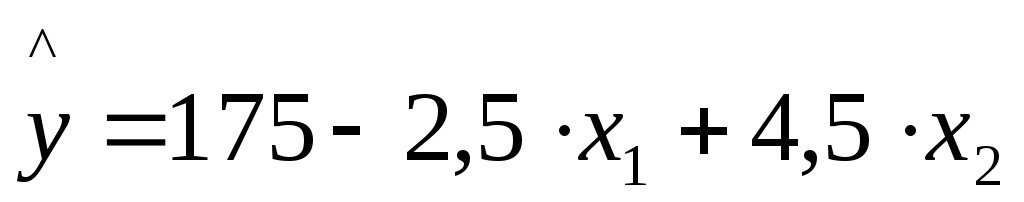.При анализе остаточных величин были использованы значения, приведенные в таблице. Требуется:

1. 
   по трем позициям рассчитать , , , , ;
   
2. 
   рассчитать критерий Дарбина – Уотсона;
   
3. 
   оценить полученный результат при 5%-ном уровне значимости;
   
4. 
   указать, пригодно ли уравнение для прогноза.
   

.

№	y	x1	x2
1	219	809	309
2	729	1009	509
3	309	1509	609
	…	…	…

Решение:

1. 
   определяется путем подстановки фактических значений x₁ и x₂ в уравнение регрессии:
   

;

;

.

Остатки _tрассчитываются по формуле 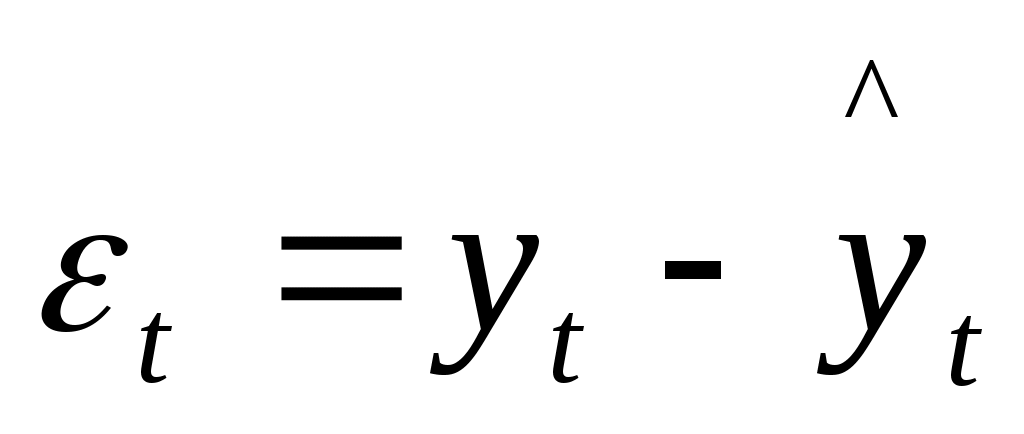. Следовательно, , , ; , , ;

- те же значения, что и _t, но со сдвигом на один месяц.

Результаты вычислений оформим в виде табл. 6.2:

Таблица 6.2

№
1	-457	676	-	-	-	456976
2	-57	786	676	110	12100	617796
3	-857	1169	786	383	146689	1366561
…	…	…	…	…	…	…
					40000	10500

2. 
   Критерий Дарбина – Уотсона рассчитывается по формуле
   

.

3. 
   Фактическое значение dсравниваем с табличными значениями при 5%-ном уровне значимости. При n=18 месяцев и m=2 (число факторов) нижнее значение dравно 1,05, а верхнее – 1,53. Так как фактическое значение d близко к 4, можно считать, что автокорреляция в остатках характеризуется отрицательной величиной. Чтобы проверить значимость отрицательного коэффициента автокорреляции, найдем величину 4–d=4–3,81=0,19, что значительно меньше, чем d. Это означает наличие в остатках автокорреляции.
   
4. 
   Уравнение регрессии не может быть использовано для прогноза, так как в нем не устранена автокорреляция в остатках, которая может иметь разные причины. Автокорреляция в остатках может означать, что в уравнение не включен какой-либо существенный фактор. Возможно также, что форма связи неточна, а может быть, в рядах динамики имеется общая тенденция.
   

Задача 10

По семи территориям Центрального района за 1995 г. известны значения двух признаков. Требуется:

1. 
   Для характеристики зависимости y от x рассчитать параметры линейной функции.
   
2. 
   Оценить каждую модель через среднюю ошибку аппроксимации и F-критерий Фишера.
   

Район	Расходы на покупку продовольственных товаров в общих расходах, %, y	Среднедневная заработная плата одного работающего, руб., x
1	75,3	55,1
2	61,2	69,0
3	60,2	67,2
4	66,7	71,8
5	62,3	68,8
6	54,3	57,2
7	59,3	65,2

Решение:

Для расчета параметров a и b линейной регрессии y=a+bx решаем систему нормальных уравнений относительно a и b:





По исходным данным рассчитываем y, x, yx, x², y²:

	y	x	yx	x2	y2			Ai
1	75,3	55,1	4149,03	3036,01	5670,09	64,76	10,54	14,0
2	61,2	69,0	4222,8	4761	3745,44	61,98	-0,78	1,3
3	60,2	67,2	4045,44	4515,84	3624,04	62,34	-2,14	3,6
4	66,7	71,8	4789,06	5155,24	4448,89	61,42	5,28	7,9
5	62,3	68,8	4286,24	4733,44	3881,29	62,02	0,28	0,4
6	54,3	57,2	3105,96	3271,84	2948,49	64,34	-10,04	18,5
7	59,3	65,2	3866,36	4251,04	3516,49	62,74	-3,44	5,8
Итого	439,3	454,3	28464,89	29724,41	27834,73	439,6		51,5
Среднее значение	64,9	62,76	4066,41	4246,34	3976,39	x	x	7,36
	6,129	5,859	x	x	x	x	x	x
2	37,57	34,33	x	x	x	x	x	x

Тогда



Уравнение регрессии: . С увеличением среднедневной заработной платы на 1 руб. доля расходов на покупку продовольственных товаров снижается в среднем на 0,2%-ных пункта.

Рассчитаем линейный коэффициент парной корреляции:

.

Связь умеренная, обратная. Определим коэффициент детерминации:

.

Вариация результата на 3,6% объясняется вариацией фактора x. На долю прочих факторов приходится 96,4%.

Подставляя в уравнение регрессии фактические значения x, определим теоретические (расчетные) значения . Найдем величину средней ошибки аппроксимации :

.

В среднем расчетные значения отклоняются от фактических на 7,36%.

Рассчитаем F-критерий:



Поскольку 1 F , следует рассмотреть F^-1. Полученное значение указывает на необходимость принять гипотезу Н₀ о случайной природе выявленной зависимости и статистической незначимости параметров уравнения и показателя тесноты связи.

Список литературы:

1. 
   Доугерти К. Введение в эконометрику: Пер. с англ. – М.: ИНФРА-М, 1999. – 402 с.
   
2. 
   Кремер Н.Ш. Эконометрика. – М.: ЮНИТИ-ДАНА, 2008. – 311 с.
   
3. 
   Магнус Я.Р. Эконометрика. Начальный курс. – М.: Дело, 2004. – 576 с.
   
4. 
   Эконометрика: Учебник / Под ред. И.И. Елисеевой. – М.: Финансы и статистика, 2002. – 344 с.
   
5. 
   Эконометрика: Учебник / Тихомиров Н.П., Дорохина Е.Ю. – М.: Издательство «Экзамен», 2003. – 512 с.