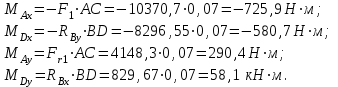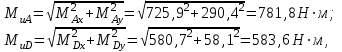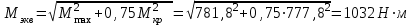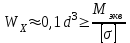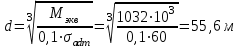техмех. тех механика 45. Задача 18
 Скачать 0.5 Mb. Скачать 0.5 Mb.
|
|
Задача 6 Дана схема трех стержней, поддерживающих абсолютно жесткую балку. Стержни имеют одинаковое поперечное сечение, состоящих из двух равнобоких уголков заданных размеров. Определить допускаемое значение силы F, приняв [σ] = 160 МПа. Весом балки пренебречь. Дано: а=1,5м, b=2м 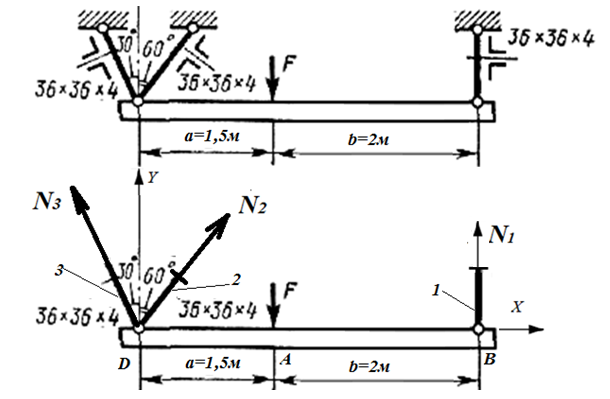 Решение: Выбираем расчетную схему, представляющую собой плоскую стержневую систему, для которой следует определить силы в стержне, используя уравнения равновесия произвольной плоской системы сил. 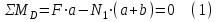 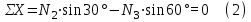 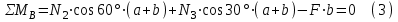 Из (1): 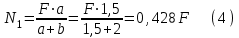 Из (2): 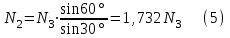 В уравнение (3) подставляем вместо N2 выражение(5): 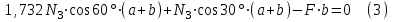 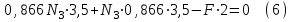 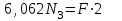 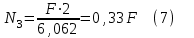 Подставляем (7) в (5), получаем: 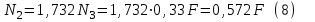 Проверяем правильность реакций N1, N2, N3. 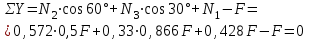 Реакции стержней определены верно. Так как все три стержня по условию имеют одинаковое поперечное сечение, то допускаемое значение силы А определяем для наиболее нагруженного стержня, каким является стержень 2. Следовательно, Nmax =N2=0,572F. Исходя из условия прочности: [F]=0,572F=[Ϭ]·2A и , учитывая, что площадь равнобокого уголка 36×36×4 А=2,67 см2, получаем значение допускаемой силы 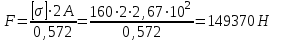 Задача № 18 Двухступенчатый стальной брус, нагружен силами F1, F2, F3. Построить эпюру продольных сил и нормальных напряжений по длине бруса. Определить перемещение ∆ℓ свободного конца бруса, приняв Е= 2∙105 МПа. Дано: F1 = 8 кН; F2 = 10кН; F3 = 12 кН; А1 = 0,6 см 2; А2 =0,4 см 2 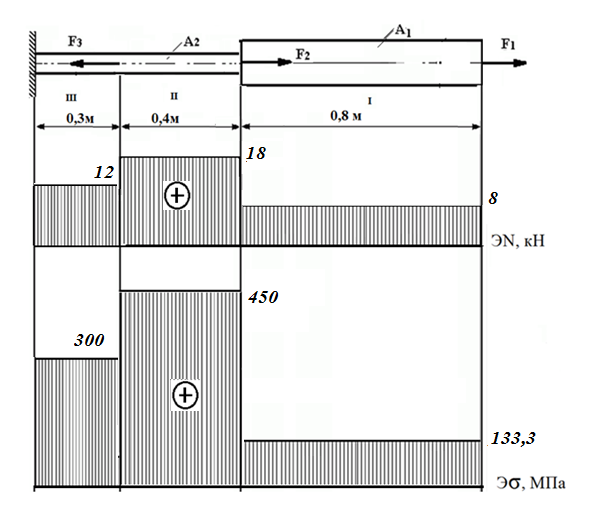 Решение Разделим брус на участки, границы которых определяются местами изменения поперечных размеров бруса или точками приложения внешних нагрузок. Рассматриваемый брус имеет три участка. Применяя метод сечений, определяем продольную силу N, выражая ее через внешние силы F1 , F2 и F3. На участке I продольная сила равна: 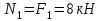 На участке II продольная сила равна: 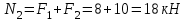 На участке III продольная сила равна: 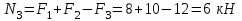 Строим эпюру продольных сил N. Определяем нормальные напряжения в поперечных сечениях по формуле: 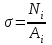 Где А – площадь поперечного сечения бруса. 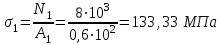 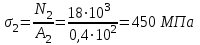 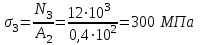 Условие прочности по всей длине бруса выполняется. Полное удлинение бруса равно алгебраической сумме удлинений его участков 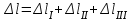 Определим их, используя формулу Гука 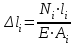 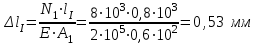 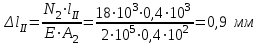 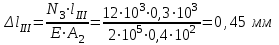 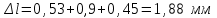 Задача № 21 Определить реакции опор двухопорной балки. Дано: F=82 Н; q=6 Н/м; М=60 Н·м Определить реакции опор RА и RВ, НА. 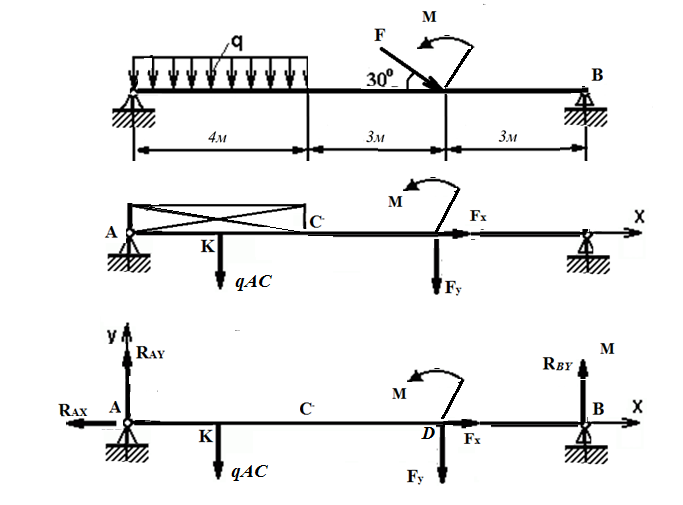 Решение: 1.Изобразим балку с действующими на неё нагрузками. 2.Изобразим оси координат Х и У. 3. Силу F заменяем её составляющими 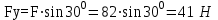 и и 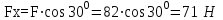 . Равнодействующая . Равнодействующая 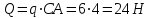 равномерно распределенной нагрузки приложена в середине участка CA, в точке К. равномерно распределенной нагрузки приложена в середине участка CA, в точке К.4. Освобождаем балку от опор, заменив их опорными реакциями. 5. Составляем уравнения равновесия статики и определяем неизвестные реакции опор. Из уравнения суммы моментов всех действующих на балку сил, составленного относительно одной из точек опор, сразу определяем одну из неизвестных вертикальных реакций: 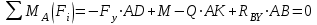 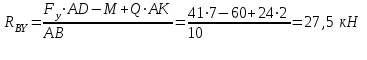 Определяем другую вертикальную реакцию: 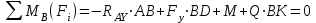 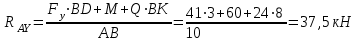 Определяем горизонтальную реакцию  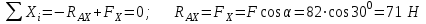 6. Проверяем правильность найденных результатов: 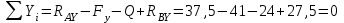 Условие равновесия 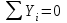 выполняется, следовательно, реакции опор найдены верно. выполняется, следовательно, реакции опор найдены верно.Задача № 35. Для двухопорной балки построить эпюры поперечных сил, изгибающих моментов и, исходя из условия прочности при [σ] = 160 МПа, подобрать необходимый размер поперечного сечения (двутавр или два швеллера) 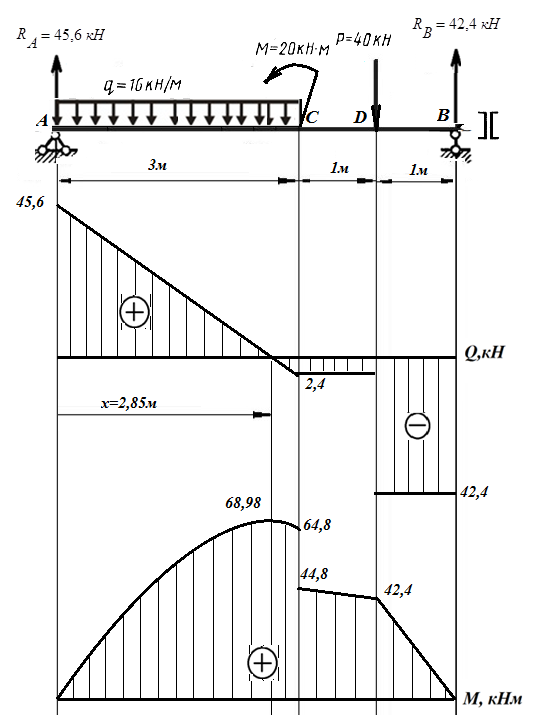 Решение: Определяем реакции опор А и В. Мысленно отбросим опоры, заменим их реакциями и составим уравнения равновесия для свободной балки. 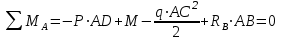 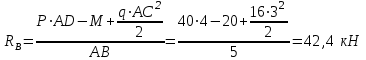 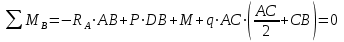 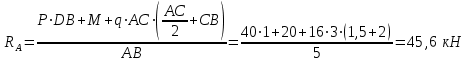 Проверка: 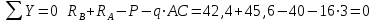 Вычисляем значения изгибающего момента Мх и поперечной силы Qy на каждом участке Участок АС   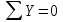 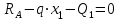 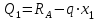 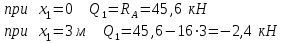 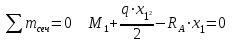 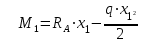 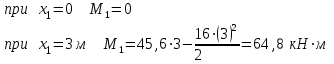 На участке АС эпюра Q меняет знак. Эпюра М имеет вид квадратной параболы, имеющей в месте перемены знака экстремум. Вычислим координаты вершины параболы. 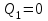 при при 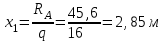 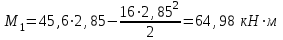 Участок СD 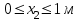 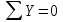 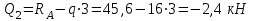 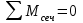 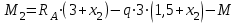 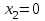 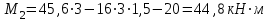 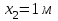 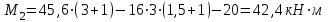 Участок BD 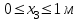 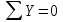 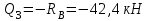 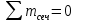 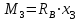 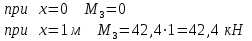 Строим эпюры Q и M. Подбор сечения осуществляется из условия прочности. Момент сопротивления всего сечения: 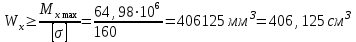 . .Момент сопротивления одного швеллера: 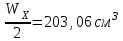 По таблице сортамента ГОСТ 8240-97 выбираем швеллер №22а, для которого Wx=212см3. Задача 45 Для стального вала постоянного поперечного сечения: 1) определить значение моментов М1, М2, М3, М4; 2) построить эпюру крутящих моментов; 3) определить диаметр из расчетов на прочность и жесткость, приняв поперечное сечение вала – круг. Считать [τк] = 30 МПа; [φ0] = 0,02 рад/м; G = 8·104 МПа. 4) окончательно принимаемое значение диаметра вала должно быть округлено до ближайшего четного или оканчивающегося на пять числа. Дано: Р 1 =90 кВт; Р 2 =25 кВт; Р3 =40 кВт; w = 20 с -1; G = 8 × 104 МПа. 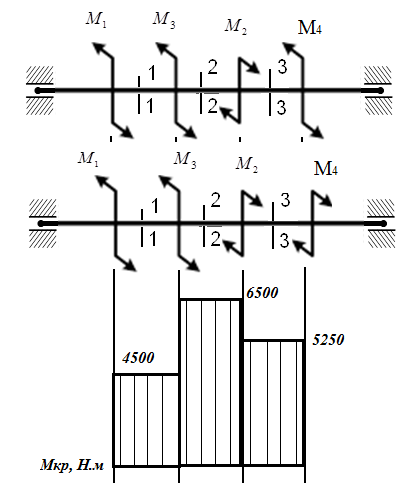 РешениеОпределяем величины скручивающих моментов М1 , М2 и М3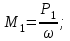 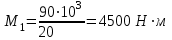 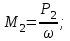 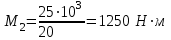 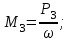 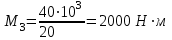 Определяем уравновешивающий момент М 2SМz = 0; М 1 - М 2 + М 3 + M4 =0;М 4 = -М 1 + М2 -M3 = -4500 + 1250 -2000= -5250 Н·м.Определим методом сечений значения крутящих моментов, действующих на участках вала между шкивами. Сечение I-I 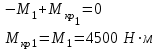 Сечение II-II 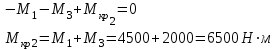 Сечение III-III 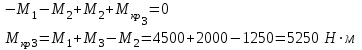 По полученным значениям строим эпюру крутящих моментов. 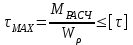 Где Wp- полярный момент сопротивления поперечного сечения вала. Для круглого сечения вала 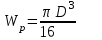 |

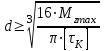
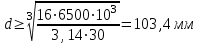
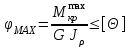
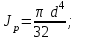
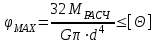
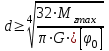
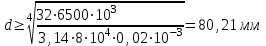
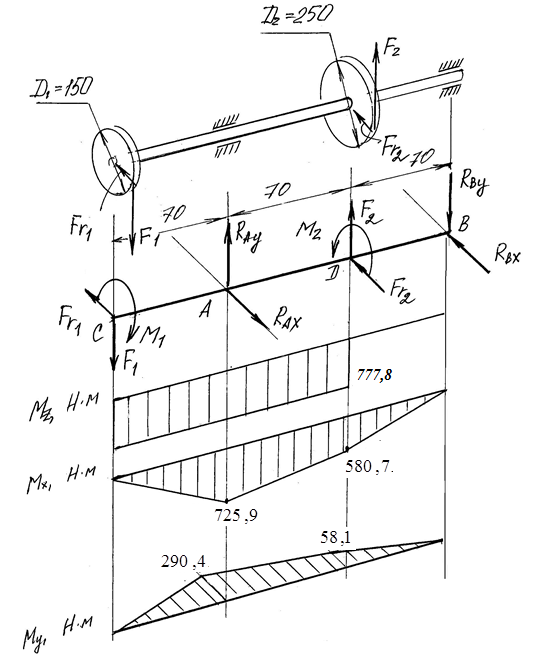
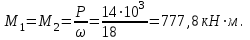
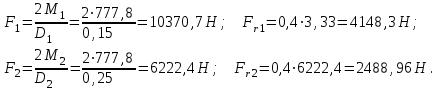

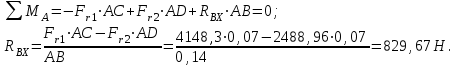
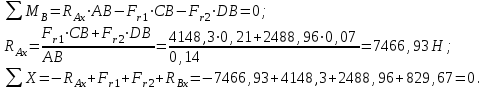
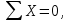 следовательно , RAx и RBх найдены верно.
следовательно , RAx и RBх найдены верно.