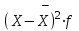статистика задачи. статка зад 2 12 34 44 54. Задача 2 3 Задача 12 13 Задача 24 16 Задача 34 19 Задача 44 23 Задача 54 26 Список использованной литературы 28
 Скачать 226.11 Kb. Скачать 226.11 Kb.
|
Задача 12Имеются данные обследования бюджетов домашних хозяйств района: Таблица 5 – Исходные данные
Определить: а) среднедушевой доход; б) моду и медиану; в) показатели вариации. Решение Данный ряд сгруппирован по размеру среднедушевого дохода. Интервалы групп являются открытыми. Величина смежных интервалов (шаг интервала) равна 500. Перепишем данную таблицу, принимая для первого и последнего интервала шаг интервала, равный 500. Таблица 6 - Расчетная
1) Средней величиной в статистике называется обобщающий показатель, характеризующий типичный уровень явления в конкретных условиях места и времени, отражающий величину варьирующего признака в расчете на единицу качественно однородной совокупности. Выбор средней определяется экономическим содержанием показателя и исходных данных. В данной задаче в каждую группу объединены одинаковые варианты, т.е. варианты имеют различный вес, поэтому вычисляется средняя арифметическая взвешенная: 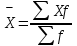 Получаем 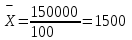 (руб.). (руб.).2) Мода - это величина признака (варианта), который наиболее часто встречается в данной совокупности, т.e. это варианта, имеющая наибольшую частоту. Моду находим по формуле: 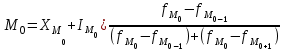 где: 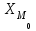 - минимальная граница модального интервала; - минимальная граница модального интервала;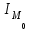 - величина модального интервала; - величина модального интервала;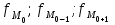 {частоты модального интервала, предшествующего и следующего за ним {частоты модального интервала, предшествующего и следующего за ним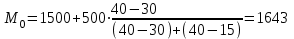 Медиана - варианта, находящаяся в середине ряда распределения. Медиану находим по формуле: 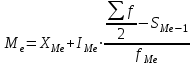 где: 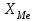 - нижняя граница медианного интервала; - нижняя граница медианного интервала;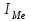 - величина медианного интервала; - величина медианного интервала;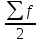 - полусумма частот ряда; - полусумма частот ряда;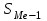 - сумма накопленных частот, предшествующих медианному интервалу; - сумма накопленных частот, предшествующих медианному интервалу;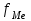 - частота медианного интервала. - частота медианного интервала.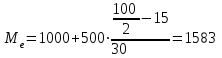 3) Коэффициент вариации 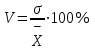 Показатель вариации отражает тенденцию развития явления, т.e. действие главных факторов. Показатель вариации выражается в процентах. Для расчетов необходимо найти среднее квадратическое отклонение. 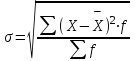 - взвешенное; - взвешенное; 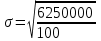 =250 =250 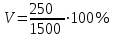 = 16,6 % = 16,6 %Коэффициент вариации используют также как характеристику однородности совокупности. Совокупность считается однородной, если коэффициент вариации не превышает 33%. В данном примере можно сделать вывод, что совокупность является однородной. |