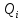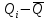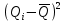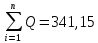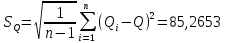Кк. МЕТРОЛОГИЯ задание для заочников (2) (1). Задача 2 Обработка экспериментальных данных Цель работы научиться обрабатывать массивы экспериментальных данных

• Название: Задача 2 Обработка экспериментальных данных Цель работы научиться обрабатывать массивы экспериментальных данных
• Дата: 10.09.2022
• Размер: 46.4 Kb.
• Имя файла: МЕТРОЛОГИЯ задание для заочников (2) (1).docx
• Тип: Задача; #670408
• страница: 2 из 3

= (3)

2. 
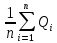   Определение среднего квадратического отклонения результата измерения: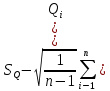
   

(4)

Расчет среднего квадратического отклонения желательно оформить в виде таблицы 3.

Таблица 3

3. Исключение ошибок по правилу трех сигм: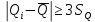



(5)

4. Если отклонение результата отдельного измерения от среднего арифметического значения больше, чем три сигма, то его считают ошибочным и его отбрасывают, после чего повторяют операции 1,2,3.

5. После исключения ошибок, допуская, что результат измерения подчиняется нормальному закону распределения вероятности, находят стандартное отклонение по формуле: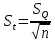

,

Вариант 64.

Исходные данные:

64

32.94

33.37

37.41

40.31

37.02

38.34

42.69

41.09

37.98

Решение.

Для решения данной задачи составим вспомогательную таблицу5.

Результаты измерения i
1	2	3
32,94	-4,96	24,6016
33,37	-4,53	20,5209
37,41	-0,49	0,2401
40,31	2,41	5,8081
37,02	-0,88	0,7744
38,34	0,44	0,1936
42,69	4,79	22,9441
41,09	3,19	10,1761
37,98	0,08	0,0064

Таблица 5

1. Среднее арифметическое значение результата
измерения равно: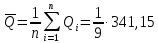

2. Среднего квадратическое отклонение результата измерения: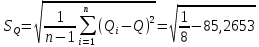

=3,26

3. Исключение ошибок по правилу трех сигм: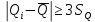

В нашем случае три сигма равно: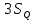

=3 3,26=9,78

Отклонение результата отдельного измерения от среднего арифметического смотрим по графе 2 таблицы 5. Значений больше, чем три сигма, нет. Значит ошибок нет.

4. Допуская, что результат измерения подчиняется нормальному закону распределения вероятности, находим стандартное отклонение: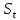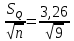

= =1,08

5. Выбираем доверительную вероятности Р, равную 0,95 и определяем квантиль распределения, т.е. параметра t по таблице 4. При Р=0,95, t=l,65.

6. Проводим расчет половины доверительного интервала: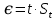

=1,65 1,08=1,782

7. Находим интервалы, в которых находится значение измеряемой величины:

37,9 - 1,782 < 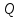< 37,9 + 1,782.

Задача № 3

Обработка результатов неравнорассеянных серии измерений

Цель работы: научиться обрабатывать результаты наравнорассеянных серии измерений

Основные положения

При обработке неравнорассеянных серий измерений с незначимым различием между средними арифметическими учитывается ценность информации,, выполненной с особой точностью.

Более точными являются серии с малой дисперсией.

Для учета важности серий измерений, выполненных с большой точностью, при определении средних арифметических двух серий измерений включают средние каждой серии с «весами».

Вес каждой серии измерений определяется как величина, обратно пропорциональная дисперсии: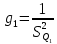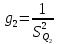

; (9)

Следовательно, среднее арифметическое

неравнорассеянных серий измерений определяется как: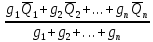

= (10)

To есть при обработке неравнорассеянных серий измерений определяется среднее арифметическое взвешенное.

Стандартное отклонение неравнорассеянных серий равно: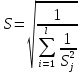

(11)

где 1 - количество серии;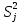

- среднее квадратическое отклонение j-й серии.

Порядок обработки экспериментальных данных, входящих в неравнорассеянные серии с незначимым различием средних арифметических, состоит из следующих этапов;

1) определение среднего арифметического каждой серии измерений:

(12)

где 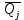- среднее арифметическое j-й серии измерений;

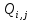- число измерений в j-й серии измерений;

- i-й результата в j-й серии измерений.

2) определение среднего квадратического отклонения каждой серии измерений: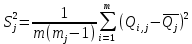

(13)

3)определение стандартного отклонения: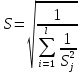

(14)

4) определение среднего арифметического взвешенного серий измерений: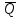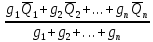

=

5) определение доверительного интервала: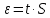


где t - параметр (квантиль) функции Стьюдента, если число измерений во всех сериях меньше 50, если нет, то параметр t определяется по таблицам функции Лапласа. Параметр (зависит от выбранной доверительной вероятности Р.

6) определение значения измеряемой величины: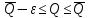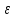

+

Задание. Произведено измерение одной и той же длины L тремя различными средствами измерений различной точности: микрометром с погрешностью 0,01 мм, штангенциркулем с погрешностью 0,02, штангенциркулем с погрешность 0,1 и получены следующие результаты, представленные в таблице 5 Определить значение измеряемой величины.

Методические указания к решению задачи

Экспериментальные данные берут по двум последним цифрам зачетной книжки в соответствии с табл. 6.

Таблица 6

Вариант	Серия	Результаты измерений
1	2	3	4	5	6	7
1	1	11.12	12.4	11.05	11.09	8.62
	2	12.08	11.75	13.11	16.38	10.48
	3	11.63	10.71	10.55	10,96	13.11
02	1	13.61	13.97	13.72	13.83	13.34
	2	13.11	13.78	13.54	12.61	12.02
	3	13.34	13.39	11.2	10.2	11.1
03	1	26.71	23.09	22.21	27.19	23.85
	2	24.92	25.12	26.05	26.96	25.95
	3	25.24	22.61	23.67	27.15	25.87
04	1	16.09	15.21	16.19	16.85	15.88
	2	16.27	16.42	17.10	8.93	15.23
	3	16.00	17.43	16.57	17.39	15.37
05	1	26.08	24.22	23.04	25.94	24.36
	2	25.77	28.03	25.47	25.82	24.37
	3	25.28	27.57	26.91	28.14	28.14
06	1	8.88	8.94	9.09	9.79	10.47
	2	11.91	10.53	9.43	11.09	10.03
	3	9.18	10.21	10.00	10.61	11.65
07	1	26.71	27.09	26.21	27.19	28.85
	2	25.85	24.92	25.12	26.05	26.96
	3	28.88	27.37	25.57	26.78	23.71
08	1	25.24	22.61	23.67	27.15	25.87
	2	23.37	19.74	13.63	30.10	28.16
	3	26.71	23.09	22.21	37.19	23.85
09	1	24,81	25.90	23.15 1	23.32	23.45
	2	24.85	24.22	23.71	32,48	25.39
	3	23.31	25.02	24.34	23.69	23.09
10	1	27.96	28.43	25.79	26.38	23.95
	2	29.1	26.09	25.21	23.19	26.85
	3	12.85	27.92	28.12	29.05	29.96
11	1	18.88	17.37	18.57	19.78	16.71
	2	18.24	17.61	18.67	18.15	18.87
	3	18.37	19.74	16.63	18.10	19.16
12	1	11.12	12.4	11.05	11.09	8.62
	2	17.43	17.81	14.68	14.78	14.79
	3	18.58	17.28	14.98	15.14	15.24
13	1	17.19	19.85	15.88	14.03	19.42
	2	22.05	22.56	21.95	21.26	24.54
	3	23.78	23.71	22.87	25.35	25.69
14	1	23.15	21.87	22.62	26.37	26.57
	2	16.10	14.16	18.57	16.97	17.29
	3	17.14	18.16	18.27	19.82	18.38
15	1	17.85	16.04	15.60	23.09	16.42
	2	14.92	16.96	17.06	17.52	17.98
	3	18.94	14.68	17.28	20.39	16.35
16	1	17.12	15.80	16.33	18.07	17.43
	2	16.18	14.37	11.31	19.55	18.58
	3	17.76	22.71	19.09	18.21	193.19
17	1	32.08	31.75	33.11	36.38	30.48
	2	31.63	30.71	30.55	30.96	33.11
	3	33.61	33.97	33.72	33.83	33.34
18	1	33.11	33.78	33.54	32.61	32.02
	2	33.34	33.39	31.2	30.2	31.1
	3	36.71	33.09	32.21	37.19	32.85
19	1	34.92	35.12	36.05	36.96	35.95
	2	35.24	32.61	33.67	37.15	35.87
	3	32.08	31.75	33.11	36.38	30.48
20	1	46.09	45.21	46119	46.85	45.88
	2	46.27	46.42	47.10	48.93	45.23
	3	46.00	47.43	46.57	47.39	45.37
21	1	56.08	54.22	53.04	55.94	54.36
	2	55.77	58.03	55.47	55.82	54.37
	3	55.28	57.57	56.91	58.14	58.14
22	1	71.88	78.94	79.09	79.79	79.47
	2	71,91	70.53	79.43	78.09	79.03
	3	70.18	70.21	79.00	79.61	79.65
23	1	81.12	82.4	81.05	81.09	80.62
	2	82.43	81.81	81.68	81.78	82.79
	3	81.58	81.28	81.98	81.14	79.24
24	1	97.19	99.85	95.88	94.03	99.42
	2	92.05	92.56	91.95	91.26	94.54
	3	93.78	93.71	92.87	95.35	95.69
25	1	66.10	64.16	68.57	66.97	67.29
	2	66.10	64.16	68.57	66.97	67.29
	3	67.14	68.16	68.27	69.82	68.38
26	1	117.85	116.04	115.60	123.09	116.42
	2	114.92	116.96	117.06	117.52	117.98
	3	118.94	114.68	117.28	120.39	116.35
27	1	217,12	215.80	216.33	218.07	217.43
	2	216.18	214.37	211.31	219.55	218.58
	3	217.76	222.71	219,09	218.21	293.19
28	1	232.08	231.75	233.11	236.38	230.48
	2	231.63	230.71	230.55	230.96	233.11
	3	233.61	233.97	233.72	233.83	233.34
29	1	333.11	333.78	333.54	332.61	332.02
	2	333.34	333.39	331.2	330.2	331.1
	3	336.71	333.09	332.21	337.19	332.85
30	1	434.92	435.12	436.05	436.96	435.95
	2	435.24	432.61	433.67	437.15	435.87
	3	432.08	431.75	433.11	436.38	430.48
31	1	546.09	545.21	546.19	546.85	545.88
	2	546.27	546.42	547.10	548.93	545.23
	3	546.00	547.43	546.57	547.39	545.37
32	1	56.08	54.22	53.04	55.94	54.36
	2	55.77	58.03	55.47	55.82	54.37
	3	55.28	57.57	56.91	58.14	58.14
33	1	71.88	78.94	79.09	79.79	79.47
	2	71.91	70.53	79.43	78.09	79.03
	3	70.18	70.21	79.00	79.61	79.65