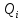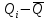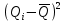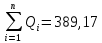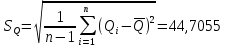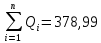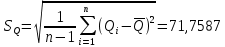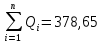Кк. МЕТРОЛОГИЯ задание для заочников (2) (1). Задача 2 Обработка экспериментальных данных Цель работы научиться обрабатывать массивы экспериментальных данных

• Название: Задача 2 Обработка экспериментальных данных Цель работы научиться обрабатывать массивы экспериментальных данных
• Дата: 10.09.2022
• Размер: 46.4 Kb.
• Имя файла: МЕТРОЛОГИЯ задание для заочников (2) (1).docx
• Тип: Задача; #670408
• страница: 3 из 3

Пример решения задачи.

Произведено измерение одной и той же длины L тремя различными средствами измерений различной точности: микрометром с погрешностью 0,01 мм, штангенциркулем с погрешностью 0,02, штангенциркулем с погрешность 0,1 и получены следующие результаты, представленные в таблице 6, вариант 33. Определить значение измеряемой величины.

Исходные данные

Вариант	Серия	Результаты измерений
33	1	71.88	78.94	79.09	79.79	79.47
	2	71.91	70.53	79.43	78.09	79.03
	3	70.18	70.21.	79.00	79.61	79.65

Решение.

Для решения данной задачи составим три вспомогательные таблицы 7, 8, 9.

Таблица 7 - Результаты первой серии измерений

Результаты измерения
1	2	3
71,88	-5,95	35,4025
78,94	1,106	1,2232
79,09	1,256	1,5775
79,79	1,956	3,8259
79,47	1,636	2,6764

1. Среднее арифметическое значение результата измерения в первой серии равно: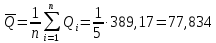



Таблица 8 - Результаты второй серии измерений

Результаты измерения
1		3
71,91	-3,888	15,1165
70,53	-5,268	27,7518
79,43	3,632	13,1914
78,09	2,292	5,2532
79,03	3,232	10,4458

Среднее арифметическое значение результата измерения во второй серии равно: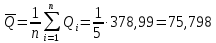



Таблица 9 - Результаты третьей серии измерений

Результаты измерения
1		3
70,18	-5,55	30,8025
70,21	-5,52	30,4704
79,0	3,27	10,6929
79,61	3,88	15,0544
79,65	3,92	15,3664

Среднее арифметическое значение результата измерения в третьей серии равно: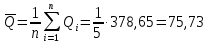



2. Среднего квадратическое отклонение результата измерения первой серии: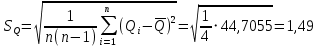



Среднего квадратическое отклонение результата измерения второй серии: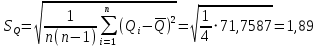



Среднего квадратическое отклонение результата
измерения третьей серии: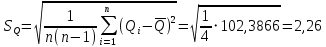



Стандартное отклонение равно: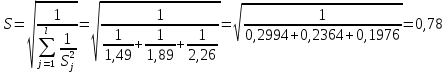



Находим вес каждой серий измерений: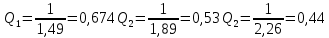



Среднее арифметическое взвешенное серии измерений: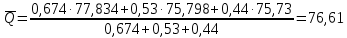


6) определение доверительного интервала: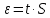


где t - параметр (квантиль) функции Стьюдента, если число измерений во всех сериях меньше 50, если нет, то параметр t определяется по таблицам функции Лапласа. Параметр t зависит от выбранной доверительной вероятности Р.

Выбираем доверительную вероятности Р, равную 0,95 и определяем квантиль распределения, т.е. параметра t по таблице 4. При Р=0,95; t=l,65. Проводим расчет половины доверительного интервала: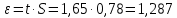


8. Находим интервалы, в которых находится значение измеряемой величины: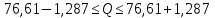