CОУТ. Задачи. Задача 3 15 Задача 5 18 Список использованных источников 22 Задание 1
 Скачать 76.67 Kb. Скачать 76.67 Kb.
|
1 2 2x1+x2=9 x1+2x2=15 Решив систему уравнений, получим: x1 = 1, x2 = 7 Откуда найдем минимальное значение целевой функции: F(X) = 200∙1 + 4∙7 = 228 Составим двойственную задачу к прямой задаче. 2y1-y2+y3-2y4≤200 y1-2y2+2y3-y4≤4 9y1-15y2+9y3-15y4 → max y1 ≥ 0 y2 ≤ 0 y3 ≥ 0 y4 ≤ 0 Отметим, что решение двойственной задачи дает оптимальную систему оценок ресурсов. Для решения двойственной задачи используем вторую теорему двойственности. Подставим оптимальный план прямой задачи в систему ограниченной математической модели: 2∙1 + 1∙7 = 9 = 9 1-ое ограничение прямой задачи выполняется как равенство. Это означает, что 1-й ресурс полностью используется в оптимальном плане, является дефицитным и его оценка согласно второй теореме двойственности отлична от нуля (y1 > 0). -1∙1 -2∙7 = -15 = -15 2-ое ограничение прямой задачи выполняется как равенство. Это означает, что 2-й ресурс полностью используется в оптимальном плане, является дефицитным и его оценка согласно второй теореме двойственности отлична от нуля (y2 > 0). 1∙1 + 2∙7 = 15 > 9 3-ое ограничение выполняется как строгое неравенство, т.е. ресурс 3-го вида израсходован не полностью. Значит, этот ресурс не является дефицитным и его оценка в оптимальном плане y3 = 0 -2∙1 -1∙7 = -9 > -15 4-ое ограничение выполняется как строгое неравенство, т.е. ресурс 4-го вида израсходован не полностью. Значит, этот ресурс не является дефицитным и его оценка в оптимальном плане y4 = 0 Поскольку x1>0, первое ограничение в двойственной задаче будет равенством. Поскольку x1>0, второе ограничение в двойственной задаче будет равенством. С учетом найденных оценок, новая система примет вид: y3 = 0, y4 = 0 2y1-y2+y3-2y4 = 200 y1-2y2+2y3-y4 = 4 9y1-15y2 → max или 2y1-y2 = 200 y1-2y2 = 4 9y1-15y2 → max Решая систему графическим способом, находим оптимальный план двойственной задачи: 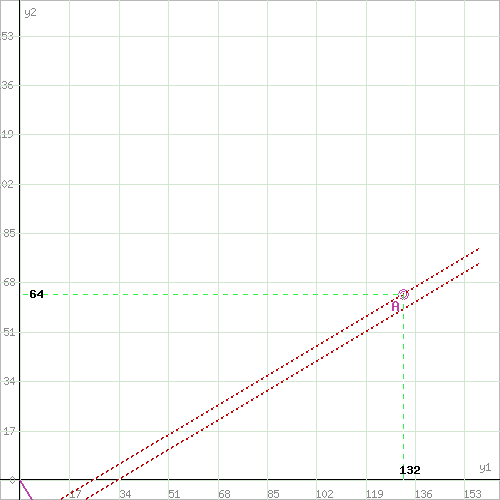 Прямая F(x) = const пересекает область в точке A. Так как точка A получена в результате пересечения прямых (1) и (2), то ее координаты удовлетворяют уравнениям этих прямых: 2y1-y2=200 y1-2y2=4 Решив систему уравнений, получим: y1 = 132, y2 = 64 Откуда найдем максимальное значение целевой функции: F(X) = 9∙132 - 15∙64 = 228 y1 = 132 y2 = 64 Z(Y) = 9∙132+(-15)∙64 = 228 Таким образом, отличную от нуля двойственные оценки имеют лишь те виды ресурсов, которые полностью используются в оптимальном плане. Поэтому двойственные оценки определяют дефицитность ресурсов Задача 3 Решить задачи линейного программирования симплекс-методом Решим прямую задачу линейного программирования симплексным методом, с использованием симплексной таблицы. Определим максимальное значение целевой функции F(X) = 2x1-x2+3x3+x4 при следующих условиях-ограничений. 2x1+x2+3x3=10 x1+x3+x4=7 3x1-2x3+x5=4 Расширенная матрица системы ограничений-равенств данной задачи: 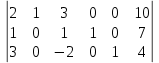 1. В качестве базовой переменной можно выбрать x2. 2. В качестве базовой переменной можно выбрать x4. 3. В качестве базовой переменной можно выбрать x5. Поскольку в системе имеется единичная матрица, то в качестве базисных переменных принимаем X = (2,4,5). Выразим базисные переменные через остальные: x2 = -2x1-3x3+10 x4 = -x1-x3+7 x5 = -3x1+2x3+4 Подставим их в целевую функцию: F(X) = 2x1-(-2x1-3x3+10)+3x3+(-x1-x3+7) или F(X) = 3x1+5x3-3 2x1+x2+3x3=10 x1+x3+x4=7 3x1-2x3+x5=4 При вычислениях значение Fc = -3 временно не учитываем. Матрица коэффициентов A = a(ij) этой системы уравнений имеет вид: 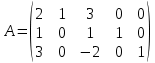 Базисные переменные это переменные, которые входят только в одно уравнение системы ограничений и притом с единичным коэффициентом. Решим систему уравнений относительно базисных переменных: x2, x4, x5 Полагая, что свободные переменные равны 0, получим первый опорный план: X0 = (0,10,0,7,4) Базисное решение называется допустимым, если оно неотрицательно.
Переходим к основному алгоритму симплекс-метода. Итерация №0. 1. Проверка критерия оптимальности. Текущий опорный план неоптимален, так как в индексной строке находятся отрицательные коэффициенты. 2. Определение новой базисной переменной. В качестве ведущего выберем столбец, соответствующий переменной x3, так как это наибольший коэффициент по модулю. 3. Определение новой свободной переменной. Вычислим значения Di по строкам как частное от деления: bi / ai3 и из них выберем наименьшее: min (10 : 3 , 7 : 1 , - ) = 31/3 Следовательно, 1-ая строка является ведущей. Разрешающий элемент равен (3) и находится на пересечении ведущего столбца и ведущей строки.
4. Пересчет симплекс-таблицы. Формируем следующую часть симплексной таблицы. Вместо переменной x2 в план 1 войдет переменная x3. Строка, соответствующая переменной x3 в плане 1, получена в результате деления всех элементов строки x2 плана 0 на разрешающий элемент РЭ=3. На месте разрешающего элемента получаем 1. В остальных клетках столбца x3 записываем нули. Таким образом, в новом плане 1 заполнены строка x3 и столбец x3. Все остальные элементы нового плана 1, включая элементы индексной строки, определяются по правилу прямоугольника. Для этого выбираем из старого плана четыре числа, которые расположены в вершинах прямоугольника и всегда включают разрешающий элемент РЭ. НЭ = СЭ - (А∙В)/РЭ СТЭ - элемент старого плана, РЭ - разрешающий элемент (3), А и В - элементы старого плана, образующие прямоугольник с элементами СТЭ и РЭ. Представим расчет каждого элемента в виде таблицы:
Получаем новую симплекс-таблицу:
1. Проверка критерия оптимальности. Среди значений индексной строки нет отрицательных. Поэтому эта таблица определяет оптимальный план задачи. Окончательный вариант симплекс-таблицы:
Оптимальный план можно записать так: x1 = 0, x2 = 0, x3 = 31/3, x4 = 32/3, x5 = 102/3 F(X) = 2∙0 -1∙0 + 3∙31/3 + 1∙32/3 = 132/3 Задача 5 Исходные данные:
Критерий максимакса ориентирует статистику на самые благоприятные состояния природы, т.е. этот критерий выражает оптимистическую оценку ситуации.
Выбираем из (33; 33; 34; 33) максимальный элемент max=34 Вывод: выбираем стратегию N=3. По критерию Байеса за оптимальные принимается та стратегия (чистая) Ai, при которой максимизируется средний выигрыш a или минимизируется средний риск r. Считаем значения ∑(aijpj) ∑(a1,jpj) = 27*0.2 + 33*0.2 + 23*0.2 + 7*0.2 + 29*0.2 = 23.8 ∑(a2,jpj) = 31*0.2 + 11*0.2 + 22*0.2 + 33*0.2 + 21*0.2 = 23.6 ∑(a3,jpj) = 33*0.2 + 32*0.2 + 16*0.2 + 13*0.2 + 34*0.2 = 25.6 ∑(a4,jpj) = 8*0.2 + 18*0.2 + 30*0.2 + 33*0.2 + 16*0.2 = 21
Выбираем из (23.8; 23.6; 25.6; 21) максимальный элемент max=25.6 Вывод: выбираем стратегию N=3. Критерий Лапласа. Если вероятности состояний природы правдоподобны, для их оценки используют принцип недостаточного основания Лапласа, согласно которого все состояния природы полагаются равновероятными, т.е.: q1 = q2 = ... = qn = 1/n. qi = 1/5
Выбираем из (23.8; 23.6; 25.6; 21) максимальный элемент max=25.6 Вывод: выбираем стратегию N=3. По критерию Вальда за оптимальную принимается чистая стратегия, которая в наихудших условиях гарантирует максимальный выигрыш, т.е. a = max(min aij) Критерий Вальда ориентирует статистику на самые неблагоприятные состояния природы, т.е. этот критерий выражает пессимистическую оценку ситуации.
Выбираем из (7; 11; 13; 8) максимальный элемент max=13 Вывод: выбираем стратегию N=3. Критерий минимального риска Севиджа рекомендует выбирать в качестве оптимальной стратегии ту, при которой величина максимального риска минимизируется в наихудших условиях, т.е. обеспечивается: a = min(max rij) Критерий Сэвиджа ориентирует статистику на самые неблагоприятные состояния природы, т.е. этот критерий выражает пессимистическую оценку ситуации. Находим матрицу рисков. Риск – мера несоответствия между разными возможными результатами принятия определенных стратегий. Максимальный выигрыш в j-м столбце bj = max(aij) характеризует благоприятность состояния природы. 1. Рассчитываем 1-й столбец матрицы рисков. r11 = 33 - 27 = 6; r21 = 33 - 31 = 2; r31 = 33 - 33 = 0; r41 = 33 - 8 = 25; 2. Рассчитываем 2-й столбец матрицы рисков. r12 = 33 - 33 = 0; r22 = 33 - 11 = 22; r32 = 33 - 32 = 1; r42 = 33 - 18 = 15; 3. Рассчитываем 3-й столбец матрицы рисков. r13 = 30 - 23 = 7; r23 = 30 - 22 = 8; r33 = 30 - 16 = 14; r43 = 30 - 30 = 0; 4. Рассчитываем 4-й столбец матрицы рисков. r14 = 33 - 7 = 26; r24 = 33 - 33 = 0; r34 = 33 - 13 = 20; r44 = 33 - 33 = 0; 5. Рассчитываем 5-й столбец матрицы рисков. r15 = 34 - 29 = 5; r25 = 34 - 21 = 13; r35 = 34 - 34 = 0; r45 = 34 - 16 = 18;
Результаты вычислений оформим в виде таблицы.
Выбираем из (26; 22; 20; 25) минимальный элемент min=20 Вывод: выбираем стратегию N=3. Проведение идеального эксперимента. В крайнем правом столбце рассчитаем средний риск.
Минимальное значение средних рисков равно 7. Следовательно, выше этой цены планирование эксперимента становится нецелесообразным. Критерий Гурвица является критерием пессимизма - оптимизма. За оптимальную принимается та стратегия, для которой выполняется соотношение: max(si) где si = y min(aij) + (1-y)max(aij) При y = 1 получим критерий Вальде, при y = 0 получим – оптимистический критерий (максимакс). Критерий Гурвица учитывает возможность как наихудшего, так и наилучшего для человека поведения природы. Как выбирается y? Чем хуже последствия ошибочных решений, тем больше желание застраховаться от ошибок, тем y ближе к 1. Рассчитываем si. s1 = 0.6*7+(1-0.6)*33 = 17.4 s2 = 0.6*11+(1-0.6)*33 = 19.8 s3 = 0.6*13+(1-0.6)*34 = 21.4 s4 = 0.6*8+(1-0.6)*33 = 18
Выбираем из (17.4; 19.8; 21.4; 18) максимальный элемент max=21.4 Вывод: выбираем стратегию N=3. Таким образом, в результате решения статистической игры по различным критериям чаще других рекомендовалась стратегия A3. Список использованных источников Грешилов А.А. Математические методы принятия решений: учеб¬ное пособие для вузов. - М.: Изд-во МГТУ им. Баумана, 2014. - 647 с. Литвак Б.Г. Разработка Управленческого решения: учебник для ву¬зов. - М.: Дело, 2008. - 439 с. Лялькина Г.Б. Математические основы теории принятия решений: учебное пособие. - Пермь: Изд-во ПНИПУ, 2012. - 118 с. Самарский А.А., Михайлов А.П. Математическое моделирование: Идеи,. Методы. Примеры. - М.: Физматлит, 2005. -316 с. 1 2 |
