|
|
Теория вероятностей. Задача 4 программирование задачи
Содержание
1. Введение ………………………………………………………………….2
2. Задача 1.4 …………………………………………………………………3
2.1 Программирование задачи…………………………………………...5
3. Задача 2.4 …………………………………………………………………9
3.1 Программирование задачи………………………………………….13
4. Задача 2.34 ………………………………………………………………15
4.1 Программирование задачи………………………………………….16
5. Задача 4.4 ………………………………………………………………..19
5.1 Программирование задачи………………………………………….20
6. Задача 5.4 ………………………………………………………………..24
7. Задача 6.4 ………………………………………………………………..26
8. Задача 7.4 ………………………………………………………………..29
9. Задача 8.4 ………………………………………………………………..31
10. Задача 9.4 ………………………………………………………………35
11. Литература ……………………………………………………………..38
1.Введение
Она рассматривает события, наступление которых заранее с полной уверенностью предсказать нельзя. Такие события называются случайными. Примеры случайных событий: появление ошибки в раздаточной ведомости, поражение мишени боеприпасом. Анализ реальных ситуаций позволяет утверждать, что каждому случайному событию можно поставить в соответствие некоторое число, которое называется вероятностью этого события. Некоторым событиям соответствует очень устойчивое значение вероятности. Например, вероятность рождения мальчика равна 0,514; бригады, работающие приблизительно в равных условиях, имеют разную производительность труда, но большая часть отдельных показателей группируется относительно наиболее характерной, наиболее часто встречающейся величины.
Индивидуальные особенности каждого события сглаживаются в большой серии однородных событий и образуют некоторую закономерность. Средний, устойчивый результат оказывается как бы неслучайным. Изучение устойчивых тенденций в случайных явлениях помогает целенаправленно влиять на их ход, ограничивать сферу случайности путем изучения факторов, влияющих на отклонения от складывающейся тенденции.
В этом состоит практическая ценность теории вероятностей. Одним из основных понятий в теории вероятностей является событие, под которым понимается всякий факт, который может произойти или не произойти. Например, событие А – это пластиковые окна заказать или обнаружение финансового нарушения при ревизии финансово-хозяйственной деятельности части, событие Б – попадание в мишень при выстреле. Различают события достоверные и невозможные.
Достоверным считается такое событие, которое обязательно должно произойти. Ему приписывается вероятность, равная единице. Невозможное событие – противоположное достоверному, т.е. такое, которое не может произойти. Ему приписывается вероятность, равная нулю. Таким образом, диапазон значений вероятностей любых событий представляет собой ряд чисел от 0 до 1.
2. Задача 1.4
Из корзины, содержащей 4 занумерованных от 1 до 4 шара, последовательно берут 2 шара без возврата. Опишите пространство элементарных исходов этого опыта, если его элементами являются двузначные числа, полученные из номеров последовательно вынутых наугад двух шаров. Опишите элементарные исходы:
а) события А –“на вынутых шарах есть шар с цифрой 3”; б) события В – «сумма цифр на вынутых шарах делится на 3». Являются ли эти события: а) несовместными; б) независимыми? Найдите вероятность этих событий Р(А) и Р(В), а также Р(А+В), Р(АВ).
|
Решение:
1. Пространство элементарных исходов:
Ω={12; 13; 14; 21; 23; 24; 31; 32; 34; 41; 42; 43}.
Общее число исходов: n=12.
2. Обозначу событие А, состоящее в появлении шара с цифрой 3. Общее число случаев n=12 (Ω={12; 13; 14; 21; 23; 24; 31; 32; 34; 41; 42; 43}; число случаев, благоприятных событию А, m=6 (А={13; 23; 31; 32; 34; 43}). Следовательно, вероятность события А вычисляется как отношение числа благоприятных случаев к общему числу случаев:
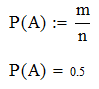
3. Обозначу событие В, состоящее в появлении шара сумма цифр которого делится на 3. число случаев n=12 (Ω={12; 13; 14; 21; 23; 24; 31; 32; 34; 41; 42; 43}; число случаев, благоприятных событию В, m=4 (В={12; 21; 24; 42}). Следовательно, вероятность события А вычисляется как отношение числа благоприятных случаев к общему числу случаев:
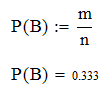
4. Ответы на вопросы:
а) Являются ли эти события несовместными?
Несколько событий называются несовместными в данном опыте, если никакие два из них не могут появиться вместе. Всего случаев у меня n=12 (Ω={12; 13; 14; 21; 23; 24; 31; 32; 34; 41; 42; 43}. У меня есть событие А={13; 23; 31; 32; 34; 43} и событие В={12; 21; 24; 42}; число благоприятных исходов m=0 (A/B ={0}).
Следовательно, вероятность событий А/В вычисляется как отношение числа благоприятных случаев к общему числу случаев:
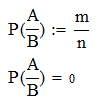
События А и В несовместны т.к. эти два события не могут появится вместе.
Б) Являются ли эти события независимыми?
Событие А называется зависимым от события В, если вероятность события А меняется в зависимости от того, произошло событие В или нет.
У меня есть два события:
- событие А ={13; 23; 31; 32; 34; 43};
- событие В ={12; 21; 24; 42}.
В данном случае вероятность события А не зависит от того, произошло событие В или нет; событие А независимо от события В.
5. Сложение вероятностей А и В. Р(А+В).
Случаи m(A) благоприятны событию А, случаи m(B) благоприятны событию В. Тогда
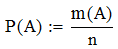 ; ; 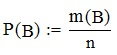
Так как события А и В несовместны, то нет таких случаев, которые благоприятны и А, и В вместе. Следовательно, событию А+В благоприятны m(A)+m(B) случаев и
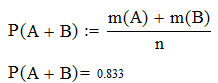
6. Умножение вероятностей А и В. Р(АВ).
Вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого, что первое имело место:
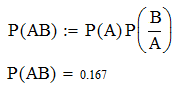
2.1 Программирование задачи
1. Программа в оболочке
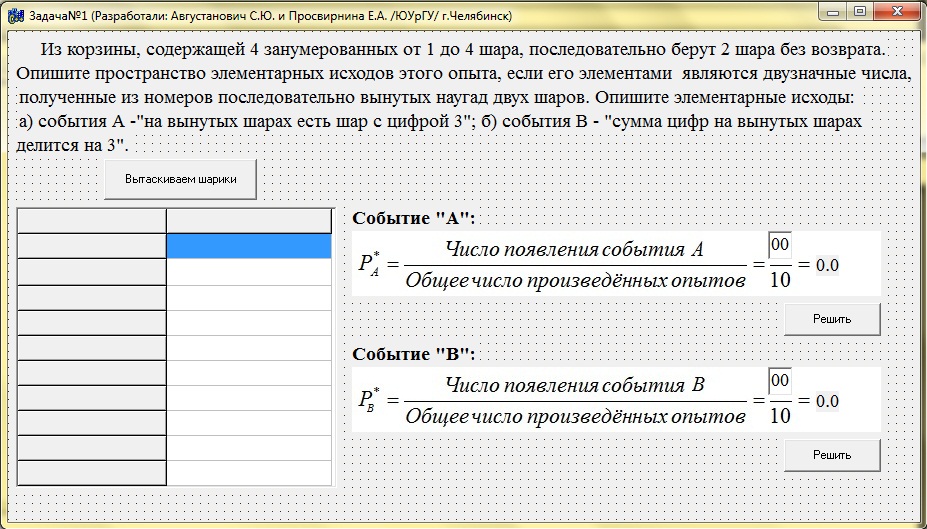
2. Код программы с описанием
//---------------------------------------------------------------------------
#include
#pragma hdrstop
#include
#include
#include
#include “s1.h”
#include
//---------------------------------------------------------------------------
#pragma package(smart_init)
#pragma resource “*.dfm”
Tform1 *Form1;
//---------------------------------------------------------------------------
__fastcall Tform1::Tform1(Tcomponent* Owner)
: Tform(Owner)
{
}
//---------------------------------------------------------------------------
void __fastcall Tform1::PyskClick(Tobject *Sender)
{
int ij, ia=1, ix, ik, iy; // Номер строки
srand(time(NULL));
// Называем столбцы
Rezyltat->Cells [0][0]=”Номер эксперимента”;
Rezyltat->Cells [1][0]=»Числа на шарике №1 и №2»;
// Вычисляю ix и ik используя при этом рэндом
for (ij=1; ij<=10; ij=ij+1)
{
ix=ia+(ij-1);
Rezyltat->Cells[0][ij]=ix;
for(int I = 0; I < 10; i++)
{
ik=1 + rand() % 45;
while(ik!=12 && ik!=13 && ik!=14 && ik!=21 && ik!=23 && ik!=24 && ik!=31 && ik!=32 && ik!=34 && ik!=41 && ik!=42 && ik!=43)
{
ik=1 + rand() % 45;
}
Rezyltat->Cells[1][ij]=ik;
}
}
}
//---------------------------------------------------------------------------
void __fastcall Tform1::Button1Click(Tobject *Sender)
{
float fn, fc;
fn=StrToFloat(n->Text); //Вводим результат эксперимента в fn
c->Caption=fn/10; //Вычисляем событие А
}
//---------------------------------------------------------------------------
void __fastcall Tform1::Button2Click(Tobject *Sender)
{
float fm, fu;
fm=StrToFloat(m->Text); //Вводим результат эксперимента в fm
u->Caption=fm/10; //Вычисляем событие А
}
//---------------------------------------------------------------------------
3. Программа в действии
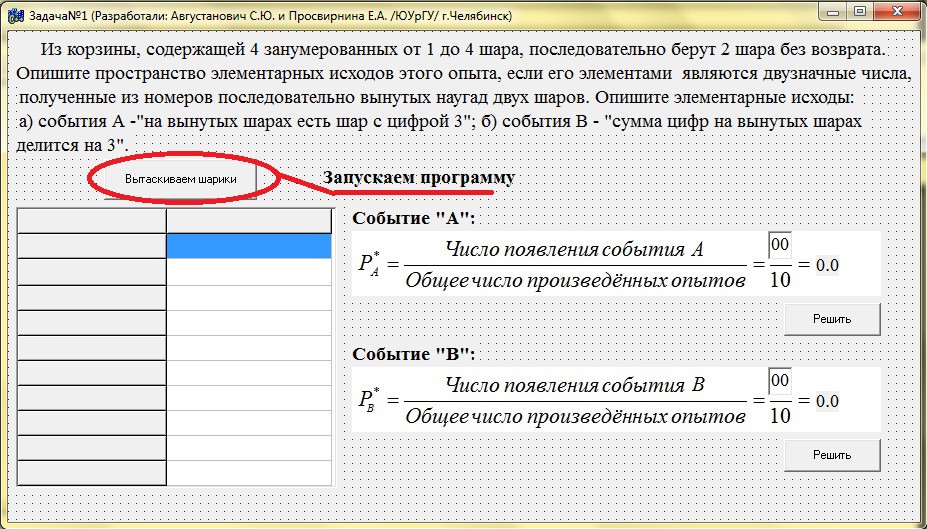
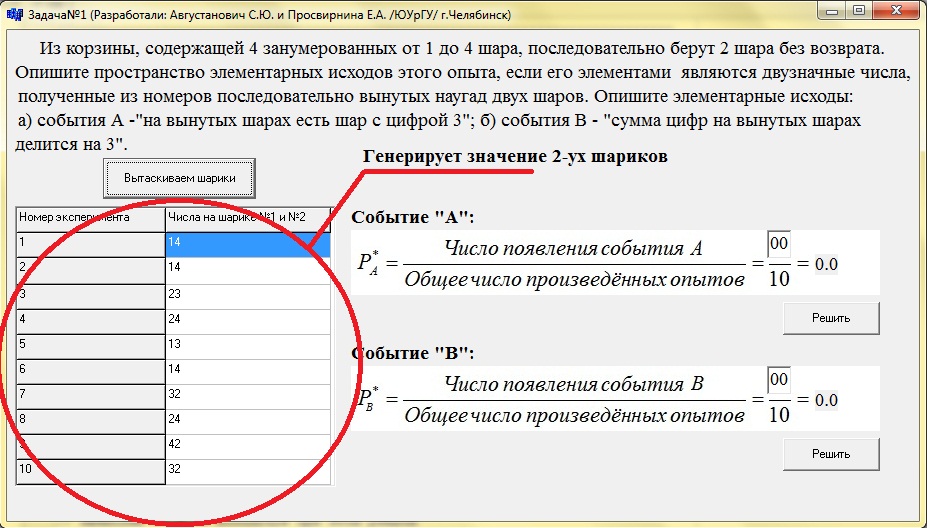
Далее мы подсчитываем сколько раз произошло событие “А” и событие “В” и забиваем в формулы.
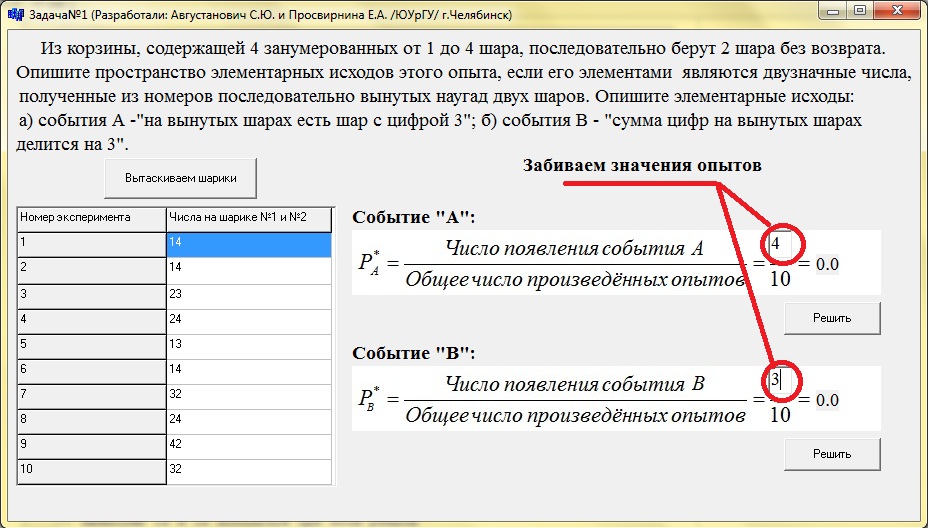
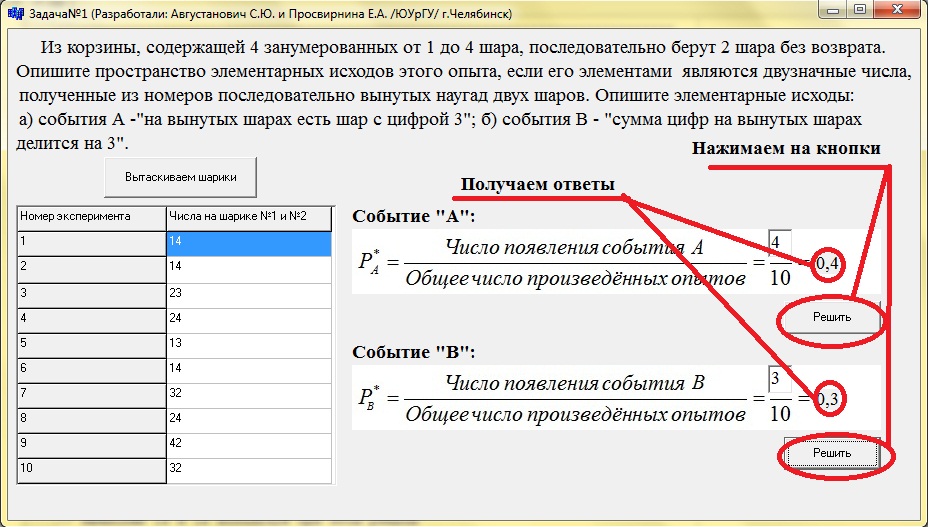
Далее нажимаем кнопку “Решить”. И получаем ответ.
3. Задача 2.4
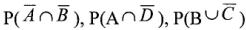 На отрезке [0,1] наудачу ставят две точки. Пусть ξ и η координаты этих точек. Рассматривают следующие события: А = (вторая точка ближе к левому концу отрезка, чем первая точка к правому); В = (корни уравнения � На отрезке [0,1] наудачу ставят две точки. Пусть ξ и η координаты этих точек. Рассматривают следующие события: А = (вторая точка ближе к левому концу отрезка, чем первая точка к правому); В = (корни уравнения �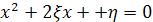 � действительны); С = {� � действительны); С = {�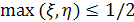 �}; D = {min� �}; D = {min�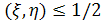 �}. Привести соответствующие рисунки и найти �}. Привести соответствующие рисунки и найти
|
Решение:
Мне дан отрезок [0,1]. На этот отрезок я ставлю две точки на удачу, где η – это координаты одной точки, а ξ – координаты другой точки.
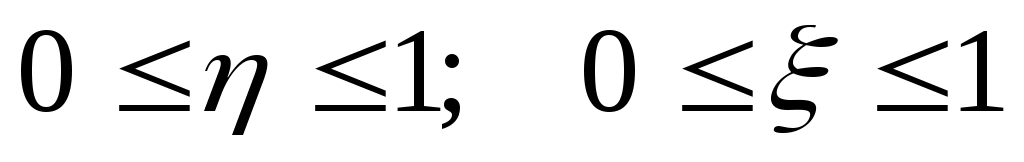
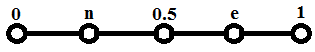
Событие А: А={ η <1- ξ }
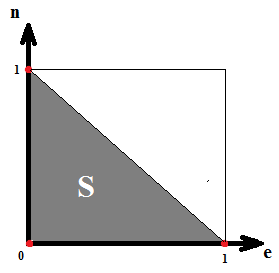
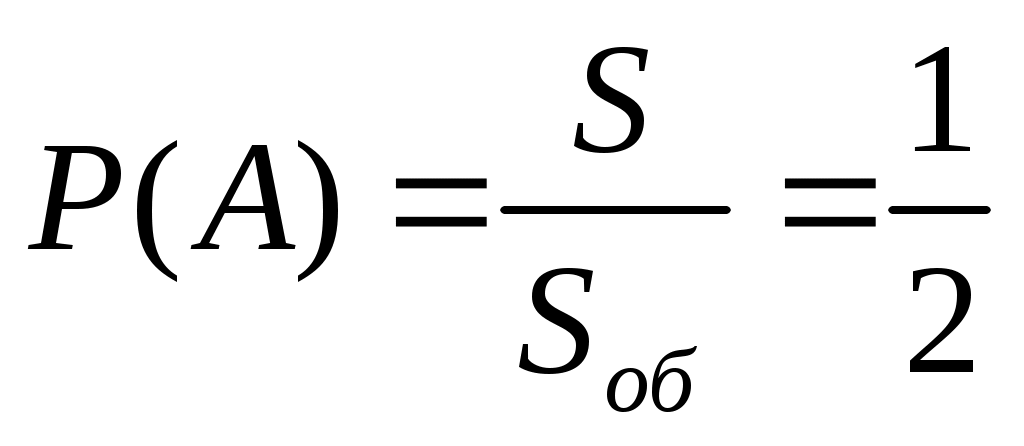 , где S – площадь закрашенной , где S – площадь закрашенной
области;
Sоб – общая площадь
квадрата.
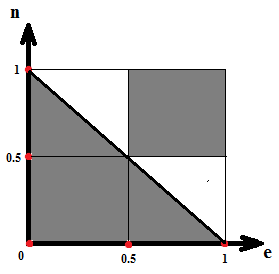
Событие В: 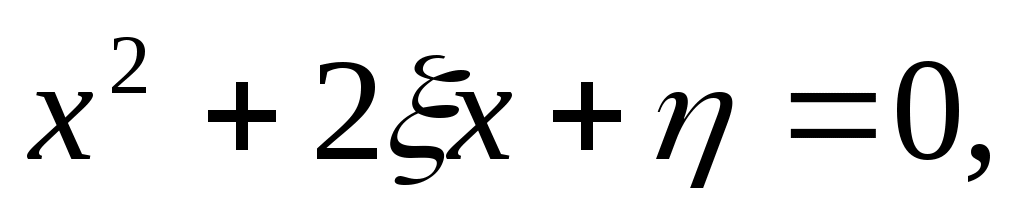
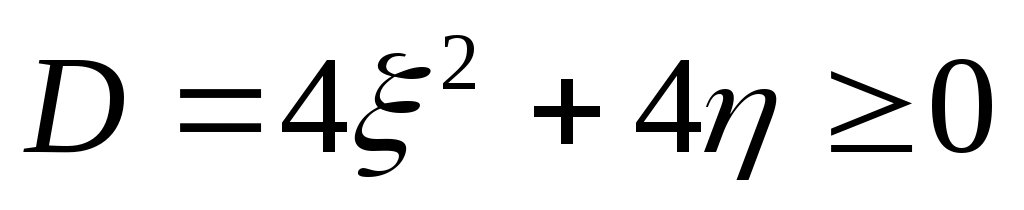
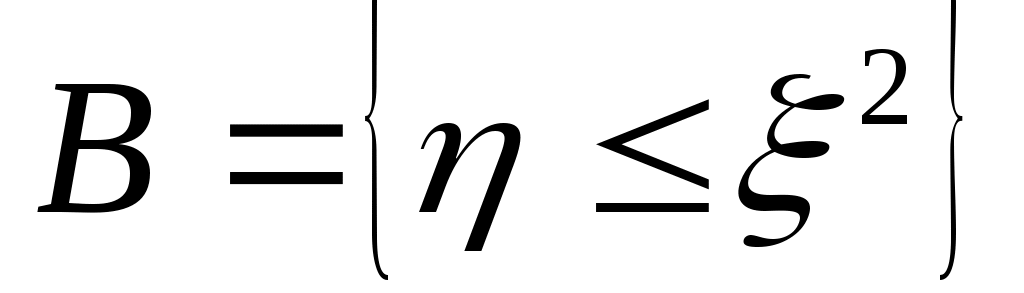
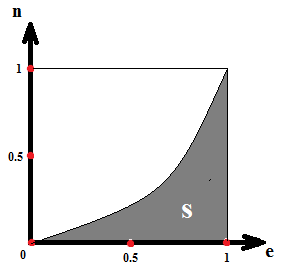 S – площадь закрашенной области, и она S – площадь закрашенной области, и она
равняется:
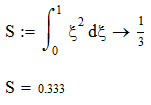
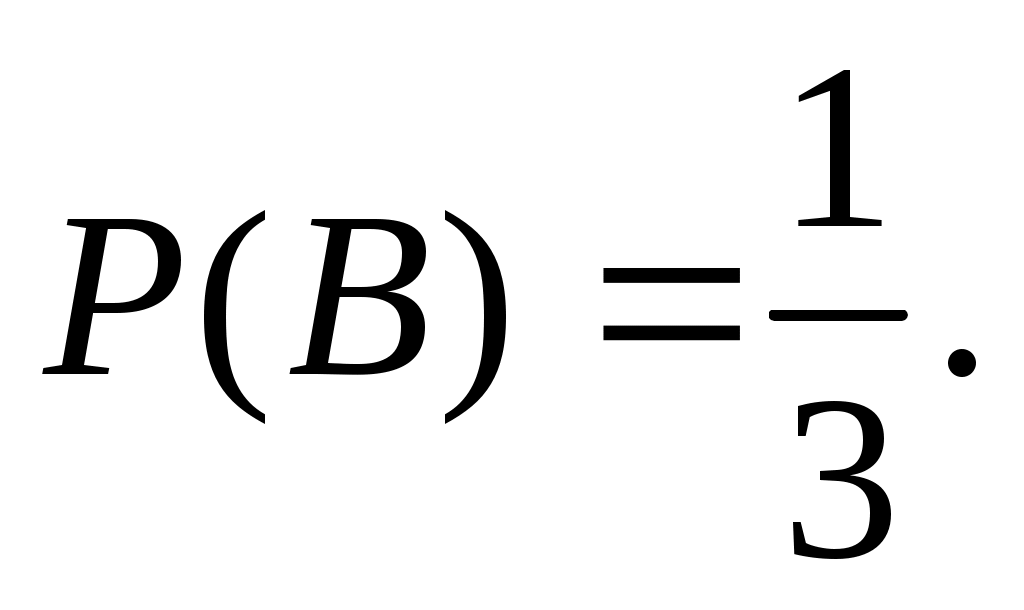
Событие С: 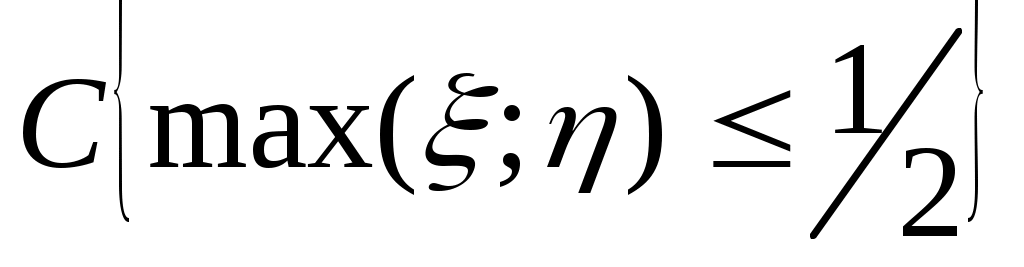
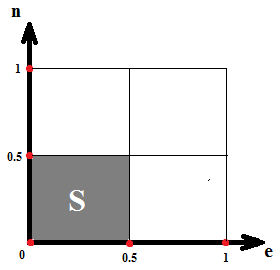
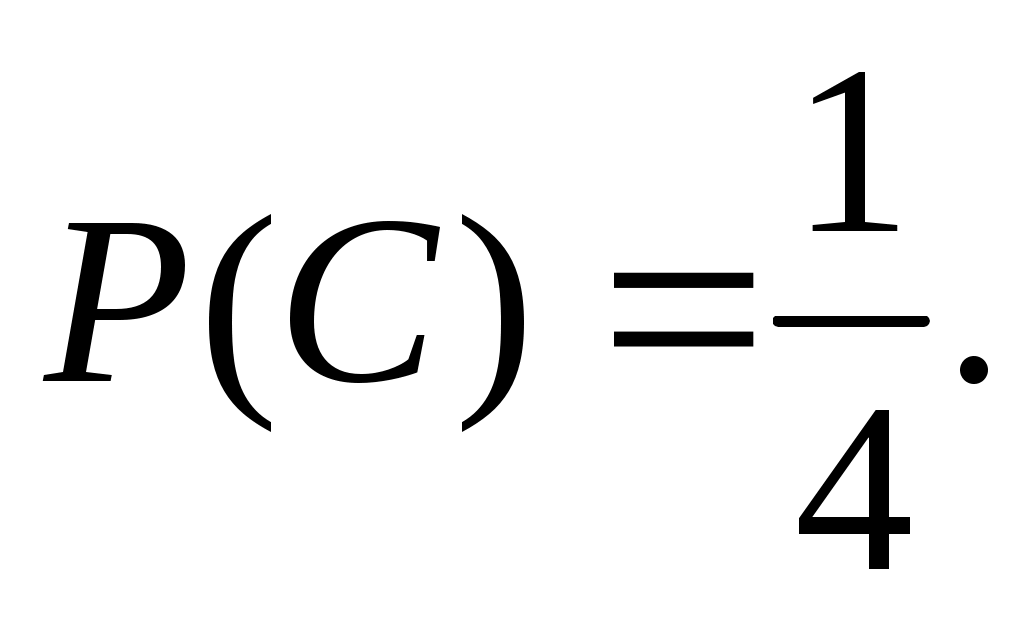
Событие D: 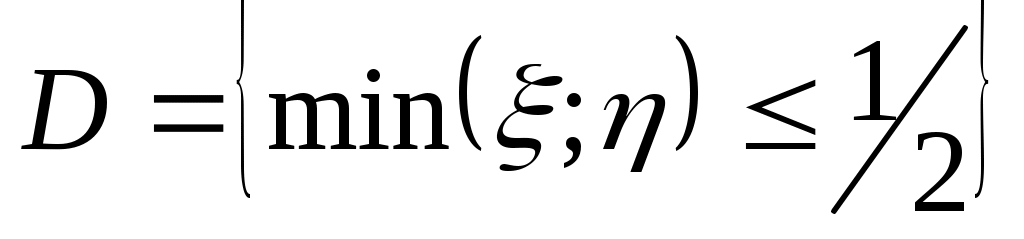
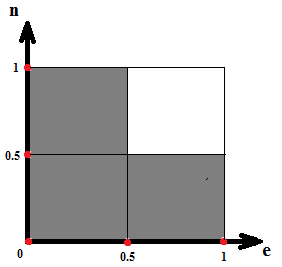
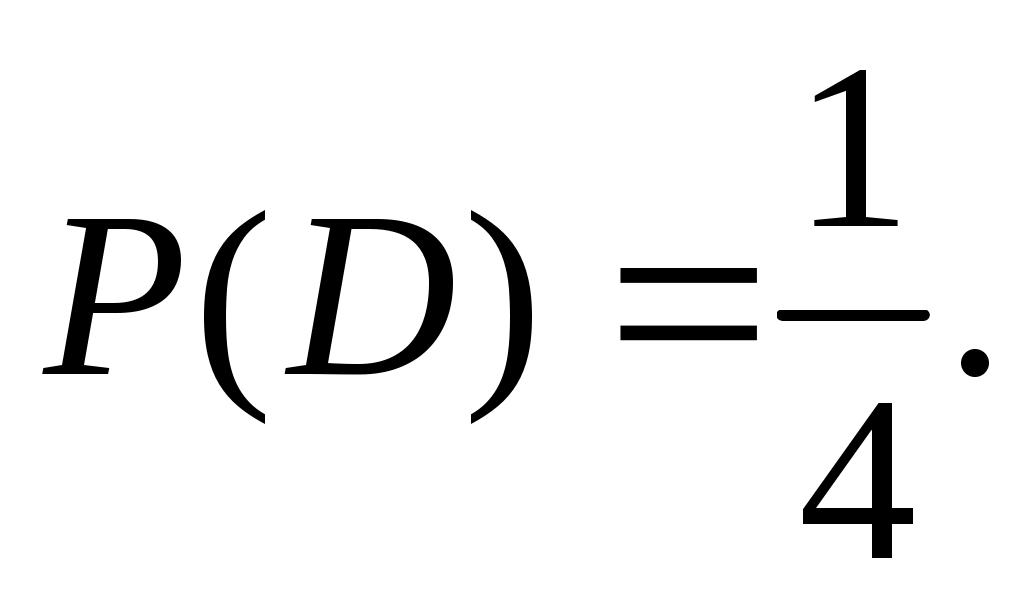
Найдём 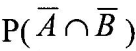 : :
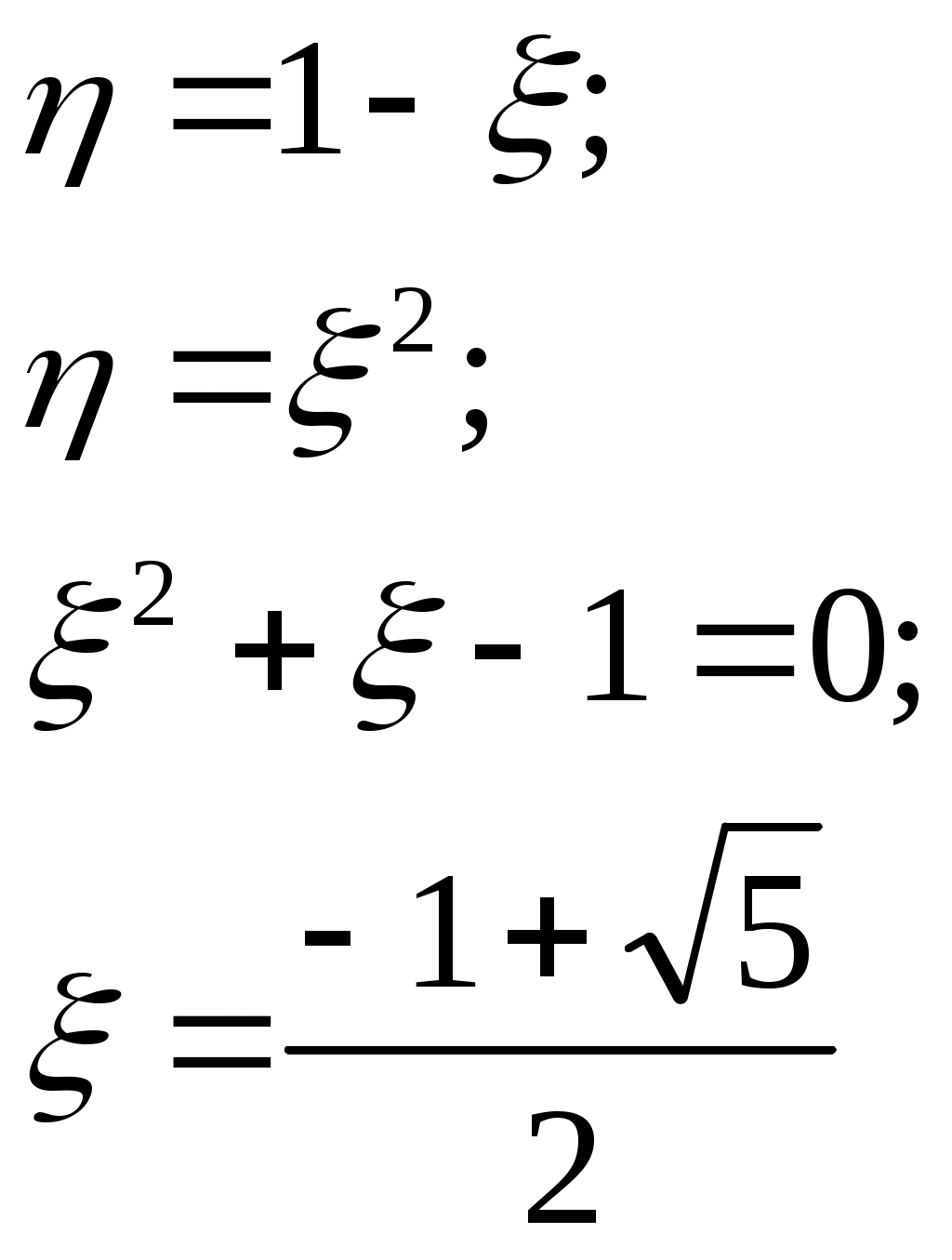 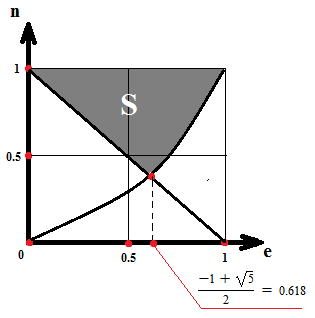
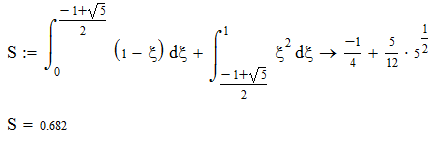
Найдём 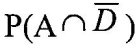 : :
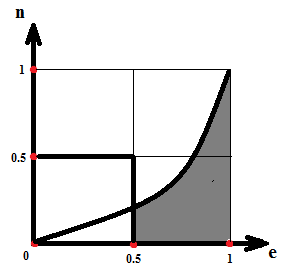
S=0 – события не совместны.
Найдём 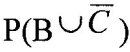 : :
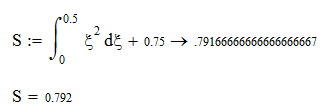
3.1 Программирование задачи
1. Код программы
#include
#include
#include
#include
#include
void Init()
{
int stime;
long ltime;
ltime=time(NULL);
stime=(unsigned) ltime/2;
srand(stime);
}
double RandomRange(double range_min, double range_max)
{
return range_min+((double)(rand())/(double)RAND_MAX)*(range_max-range_min);
}
int main()
{
int count,res=0,I;
double r,a,b;
Init();
printf(«Введите число повторений: «);
scanf(«%d»,&count);
printf(“Подождите!\n”);
for(i=0;i
{
a=RandomRange(2,4);
b=RandomRange(2,4);
r=sqrt(a*a+b*b);
if(r>=2+sqrt(2)/2 && r<=4-sqrt(2)/2)
res++;
}
printf(“Статистическая вероятность: %lf”,(double)res/(double)count);
getch();
return 0;
}
2. Результат программы
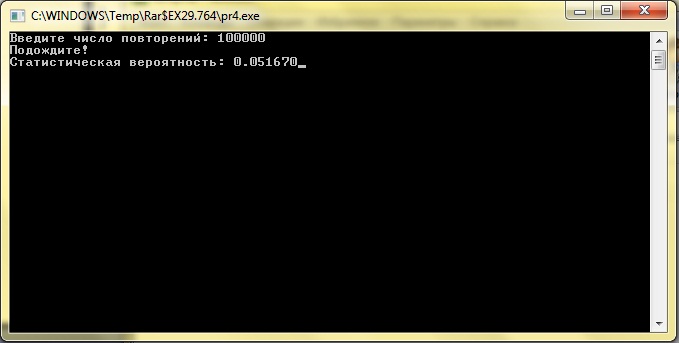
4. Задача 2.34
Наудачу взяты два положительных числа Х и Y, каждое из которых не превышает единицы. Найти вероятность того, что сумма Х + Y не превышает 1, а произведение ХY не меньше 0,09.
|
Решение:
Эта задача на геометрическую вероятность. Надо вычислить площадь S области между прямой х+у=1 и гиперболой ху=0.09. Поэтому эту площадь надо поделить на площадь единичного квадрата, т.е. на 1.
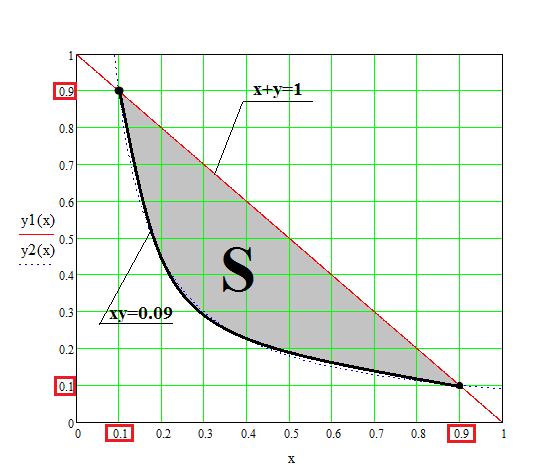
В результате получим вероятность:
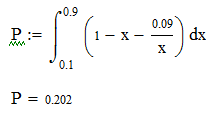
P = 0.202*100% = 20%
Ответ: вероятность того, что сумма Х + Y не превышает 1, равна 20%
4.1 Программирование задачи
1. Программа в оболочке
2. Код программы с описанием
//---------------------------------------------------------------------------
#include
#pragma hdrstop
#include “zad3.h”
//---------------------------------------------------------------------------
#pragma package(smart_init)
#pragma resource “*.dfm”
Tform1 *Form1;
//---------------------------------------------------------------------------
__fastcall Tform1::Tform1(Tcomponent* Owner)
: Tform(Owner)
{
}
//---------------------------------------------------------------------------
void __fastcall Tform1::KnopkaClick(Tobject *Sender)
{
//Определяем переменные вещественного типа
float fx, fy, fz, fk, fj;
/* Преобразовываем текстовые значения числа в вещественные значения и
присваиваем их переменным вещественного типа */
fx=StrToFloat(x->Text);
fy=StrToFloat(y->Text);
if (fx>1||fy>1||fx<0||fy<0)
{
ShowMessage («Значение первого или второго числа превышает 1 или число отрицательно»);
Abort();//Генерация «молчаливого» исключения
}
else
//Нахожу сумму и произведение чисел
fz=fx+fy;
fk=fx*fy;
fj=0.202;
//Преобразовываем вещественное значение к текстовому значению и выводим его
z->Caption= FloatToStr(fz);
k->Caption= FloatToStr(fk);
j->Caption= FloatToStr(fj);
if (fz>1||fk<0.09)
{
ShowMessage («Значение суммы чисел превышает 1 или произведение меньше 0,09»);
Abort();//Генерация «молчаливого» исключения
}
}
//--------------------------------------------------------------------------- | |
|
|
 Скачать 2.93 Mb.
Скачать 2.93 Mb.