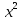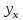контрольная. Задача 5 Задача 8 Задача 10 Задача 11 Задача 12 Задача 14 Задача 15
 Скачать 67 Kb. Скачать 67 Kb.
|
1 2 Задача 3.1. 2 Задача 3.2. 5 Задача 3.3. 8 Задача 3.4. 10 Задача 3.5. 11 Задача 3.6. 12 Задача 3.7. 14 Задача 3.8. 15 18. Статистика цен и тарифов 16 Вариант 3 Задача 3.1.Данные дохода за октябрь 100 рабочих из 1000, определенные случайной бесповторной выборкой
Определить: Среднемесячный доход у работника данного предприятия, гарантируя результат с вероятностью 0,997. Долю рабочих предприятия имеющих доход 6800 руб. и выше, гарантируя результат с вероятностью 0,954. Необходимую численность выборки при определении среднего месячного дохода работников предприятия, чтобы с вероятностью 0,954 предельная ошибка выборки не превышала 100 руб. Необходимую численность выборки при определении доли рабочих с размером месячного дохода 6800 и выше, чтобы с вероятностью 0,954 предельная выборка не превышала 4%. Решение: Средний месячный доход по выборке 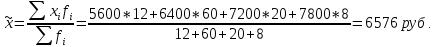 Определяем дисперсию выборочной средней 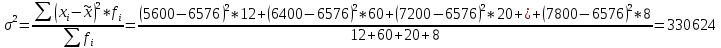 Предельная ошибка выборки при вероятности p = 0.997, t = 3 составит: 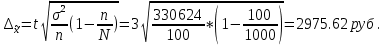 Доверительный интервал среднего размера месячного дохода работников предприятия 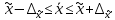 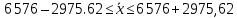 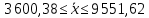 Следовательно, с вероятностью 0,997 можно утверждать, что среднемесячный размер дохода у работников данного предприятия находится в пределах от 3 600,38 до 9 551,62 руб. Определим долю рабочих (w), имеющих размер месячного дохода 6800 руб. и выше: 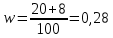 Предельная ошибка выборки при вероятности р=0,954 t=2 составит: 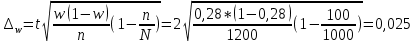 Устанавливаем доверительные интервалы для генеральной доли: 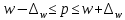 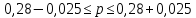 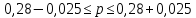 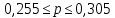 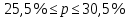 С вероятностью 0,954 можно гарантировать, что доля рабочих предприятия имеющих месячный доход 6800 руб. и выше, находится в пределах от 25,5 до 30,5 %. Необходимая численность выборки для определения среднего месячного дохода определяется по формуле: 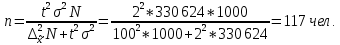 Необходимая численность выборки для определения доли рабочих, имеющих доход 1400 руб. и выше, определяется по формуле: 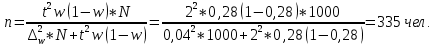 Ответ: 1) в пределах от 3 600,38 до 9 551,62 руб; 2) в пределах от 25,5 до 30,5 %; 3) 117 чел.; 4) 335 чел. Задача 3.2. По 10 однородным предприятиям имеются следующие данные:
Найдите уравнение корреляционной связи между выработкой и электровооруженностью труда. Проанализируйте параметры уравнения регрессии. Изобразите корреляционную связь графически. Решение: Зависимость между электровооруженностью труда и продукцией на одного работающего – линейная и выражается уравнением прямой 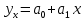 где yх – выпуск готовой продукции на одного работающего; x – электровооруженность труда на одного работающего; a0 и a1 - параметры уравнения регрессии. Для определения параметров уравнения регрессии строим расчетную таблицу.
Подставим в систему нормальных уравнений фактические данные из таблицы: 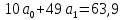 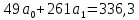 Решаем систему нормальных уравнений в следующей последовательности: домножим каждый член первого уравнения на 4,9 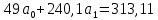 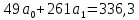 Вычтем из второго уравнения первое и получим оттуда 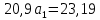 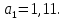 Подставим значение а1 в первое уравнение, получим а0 = 0,95. Уравнение корреляционной связи примет вид: 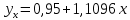 После определения параметров уравнения регрессии рассчитываем теоретическую линию регрессии ух путем подстановки значений х в уравнение корреляционной связи: 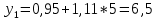 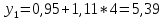 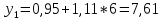 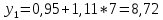 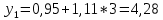 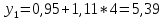 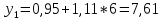 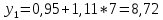 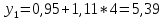 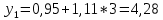 Если параметры уравнения связи определены правильно, то 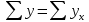 Окончательная проверка правильности расчета параметров уравнения связи производится подстановкой а0 и а1 в систему нормальных уравнений. Используя уравнение корреляционной связи yx = a0 + a1x, можно определить теоретическое значение ух для любой промежуточной точки (теоретическое значение выпуска готовой продукции на 1 работающего для любого промежуточного значения электровооруженность труда на 1 работающего). Коэффициент регрессии а1 уточняет связь между х и у. Он показывает, но сколько единиц увеличивается результативный признак при увеличении факторного признака на единицу. В нашем примере а1 = 1,11. Значит, при увеличении электровооруженности труда на 1 работающего на 1 кВтч выпуск продукции увеличивается на 1,110 тыс. руб. Задача 3.3. Данные о приеме студентов в высшие учебные заведения России
Определить отсутствующие данные и заполнить таблицу. Решение: Абсолютный прирост характеризует увеличение (уменьшение) уровня ряда за определенный промежуток времени. Он опреде-ляется по формуле: 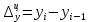 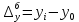  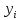 – количество принятых студентов в текущем году, – количество принятых студентов в текущем году, 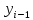 - количество принятых студентов в предыдущем году, - количество принятых студентов в предыдущем году, 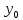 - количество принятых студентов в базисном году, в нашем случае в 2003 году. - количество принятых студентов в базисном году, в нашем случае в 2003 году.Темп роста всегда положителен. Между цепным и базисным темпами роста существует определенная взаимосвязь: произведение цепных коэффициентов роста равно базисному коэффициенту роста за весь период, а частное от деления последующего базисного темпа роста на предыдущий равно цепному темпу роста. 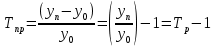 Абсолютное значение 1% прироста (А%) - это отношение абсолютного прироста к темпу прироста, выраженный в процентах и показывает значимость каждого процента прироста за тот же период времени: 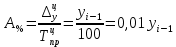 Абсолютное значение одного процента прироста равно сотой части предыдущего или базисного уровня. Оно показывает, какое абсолютное значение скрывается за относительным показателем - одним процентом прироста. Задача 3.4. Данные к расчету индекса товарооборота
Определить индекс товарооборота, индекс цены. Решение: Индекс товарооборота определяется по формуле: 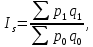 где p1, p0 – цены на товары в отчетном и базисном периодах; q1, q0 – количество проданного товара в отчетном и базисном периодах. 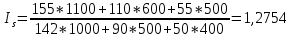 Данный индекс характеризует изменение стоимости совокупности проданных товаров в среднем в одном периоде по сравнению с другим. Т.е. стоимость проданных товаров в отчетном году вырастет на 27,54% по сравнению с базисным годом. Индекс цен - статистический показатель, применяемый для измерения динамики цен во времени и пространстве, представляет относительную величину. 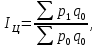 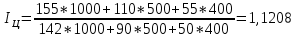 Таким образом, стоимость товаров базисного года возросла в отчетном году на 12,08%. Ответ: 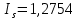 ; ; 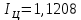 . .Задача 3.5. На 1.01.2013 года численность населения области в рабочем возрасте составила 1053,27 тыс. чел., в т.ч. численность официально зарегистрированных неработающих трудоспособных лиц, ищущих работу составила 17,6 тыс. чел. В течение года выбыло трудовых ресурсов 108,71 тыс. чел., вступило в рабочий возраст – 207,02 тыс. чел. Определить численность трудовых ресурсов на конец года. Решение: Общая численность трудовых ресурсов на конец года определяется, исходя из численности трудовых ресурсов на начало года и прироста (выбытия) численности по различным причинам в течение года: 1 053,27-17,6-108,71+207,02 = 1 133,98 тыс. чел. Ответ: численность трудовых ресурсов на конец года составляет 1 133,98 тыс. чел Задача 3.6. Имеются следующие данные за год по заводам одной промышленной компании:
На основании приведенных данных составьте групповую таблицу зависимости выработки на одного рабочего от величины заводов по числу рабочих. Число групп – три. Решение: Величина интервала рассчитывается по следующей формуле: 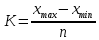 , ,где 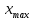 , , 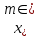 – максимальное и минимально значения объема продукции, n – количество групп. – максимальное и минимально значения объема продукции, n – количество групп.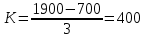 Получаем три группы с интервалом 400 чел. 1 группа от 700 до 1100 чел., 2 группа от 1100 до 1500 чел., 3 группа от 1500 до 1900 чел. Показатель выработки на одного рабочего рассчитывается по формуле: 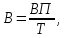 где ВП – выпуск продукции; Т – численность рабочих. Далее упорядочим исходную таблицу по возрастанию среднегодовой стоимости основных производственных фондов, выделим группы, в которые попадут заводы:
По данным рабочей таблицы составляем аналитическую группировку:
Вывод: С увеличением количества рабочих увеличиваются основные фонды и выработка на одного рабочего. Задача 3.7. Планом промышленного предприятия предусматривалось снижение затрат на 1 рубль товарной продукции на 4 %, фактически затраты возросли на 2 %. Вычислите относительную величину выполнения плана. Решение: Перечисленные в условии относительные величины связаны между собой таким соотношением: 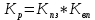 Кр=Кпз*Квп, где Кр – коэффициент роста, Кпз – коэффициент планового задания, Квп – коэффициент выполнения плана. Из приведенной формулы выражаем коэффициент выполнения плана: 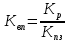 Планом промышленного предприятия предусматривалось снижение затрат на 1 рубль товарной продукции на 4%. 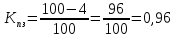 Фактически затраты возросли на 2%. 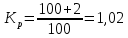 Вычисляем относительную величину выполнения плана: 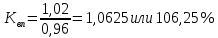 Таким образом, фактическая величина затрат оказалась больше, чем было запланировано, на 6,25%, это в свою очередь, означает что план недовыполнен на 6,25%. Задача 3.8. Вычислите среднемесячный процент брака по заводу за второй квартал по следующим данным:
Решение: Среднемесячный процент брака по заводу за второй квартал вычислим по следующей формуле: 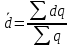 где d – доля брака, q – выпуск готовой продукции 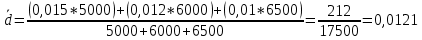 или 1,21% или 1,21%Ответ: Среднемесячный процент брака по заводу за второй квартал составляет 1,21% . 1 2 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||