Проверено 8.11.2020 Курсовая. Задача 8 3 Анализ содержания темы Вписанные и описанные четырёхугольники
 Скачать 0.7 Mb. Скачать 0.7 Mb.
|
1.3 Анализ содержания темы «Вписанные и описанные четырёхугольники»Проведем анализ теоретического, задачного материала по данной теме. Для исследования были рассмотрены учебники геометрии, рекомендованные Министерством Образования и Науки Российской Федерации к применению в образовательном процессе в общеобразовательных учреждениях. Это учебники: Атанасян Л. С. и др. «Геометрия 7-9»[4]; Шарыгин И. Ф. «Геометрия 7 - 9» [23]; Погорелов А. В. «Геометрия 7 - 9» [18] (учебники, выпущенные Министерством Образования и Науки РФ к использованию в образовательном процессе в общеобразовательных учреждениях на 2016/2017 учебный год). А также рассмотрен учебник под редакцией Смирновой И. М. «Геометрия 7 - 9»[22]. Наиболее подробно тема «Вписанные четырехугольники» изложена в учебнике Игоря Федоровича Шарыгина в параграфе 8.5 «Вписанные и описанные четырехугольники». В остальных учебниках таких параграфов нет. Понятие вписанных и описанных четырехугольников вводится в 8 классе. Параграф начинается с определений: Четырехугольник называется вписанным, если его вершины расположены на одной окружности. Четырехугольник называется описанным, если все его стороны касаются одной окружности. Далее в пункте «Вписанный четырехугольник» для рассмотрения предлагается теорема с доказательством. Теорема 8.5 (свойства и признаки вписанного четырехугольника): Для того чтобы четырехугольник ABCD был вписанным, необходимо и достаточно выполнения любого из следующих условий: а) ABCD – выпуклый четырехугольник и ABD ACD; б) сумма двух противоположных углов четырехугольника равна 180˚. Приведем доказательство данной теоремы. 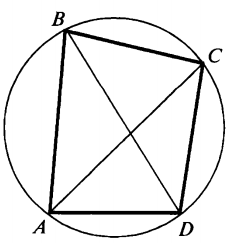 Рис. 1 Вписанный четырёхугольник ABCD Доказательство. а) Необходимость. Если ABCD – вписанный четырёхугольник (рис.1), то он непременно выпуклый и углы ABD и ACD равны, поскольку опираются на одну дугу. Достаточность. Так как ABCD выпуклый четырёхугольник, то точки B и C расположены по одну сторону от прямой AD. 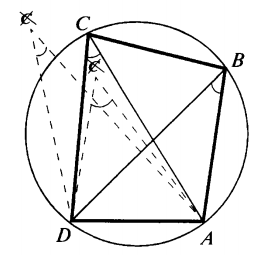 Рис.2 Описанная окружность Опишем вокруг треугольника ABD окружность (рис.2). Точка С не может располагаться вне этой окружности, так как в этом случае угол ACD, как угол с вершиной вне круга, измерялся бы полуразностью дуги AD и ещё какой-то дуги, т.е., был бы меньше угла ABD. Точно также точка С не может находиться внутри круга, так как в этом случае угол ACD был бы больше угла ABD. Значит, точка С лежит на окружности, описанной около четырёхугольника ABCD, и этот четырёхугольник является вписанным. б) Необходимость следует из свойств вписанных углов. Достаточность. Из условия следует, что все углы четырёхугольна меньше 180o, т.е. он выпуклый. Далее рассуждаем так же, как и в пункте а). Рассмотрим два противоположных угла B и D. Их сумма равна 180o. Опишем около треугольника АВС окружность (рис.3). 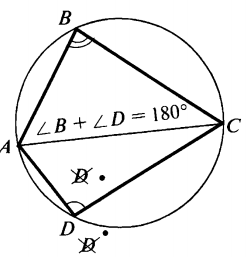 Рис.3 Описанная окружность вокруг треугольник АВС Точка D расположена по другую сторону от прямой АС, чем В. Но для всех точек дуги АС, не содержащей В, вписанные углы дополняют до 180о угол В. Значит D, не может быть ни вне, ни внутри круга. Таким образом, точка D лежит на окружности, описанной около треугольника АВС и четырехугольник ABCD вписанный. Сразу же после параграфа представлен материал, относящийся к практической части по данной теме: задачи, задания, вопросы. Представим некоторые задания, дополняющие теорию. 1082 (в). Четырехугольник ABCD вписан в окружность, P – точка пересечения диагоналей четырехугольника. Докажите, что AP PC BP PD. Если пересечение лежит внутри, равенство означает, что произведение отрезков, на которые точка P делит одну диагональ, равно произведению отрезков другой диагонали. Это утверждение известно как теорема о пересекающихся хордах, поскольку диагонали вписанного четырёхугольника являются хордами описанной окружности. В учебнике геометрии под редакцией Л. С. Атанасяна нет отдельных разделов «Вписанные и описанные четырехугольники». О них говорится в параграфе 4 «Вписанная и описанная окружность» главы XIII. В пункте 75 «Описанная окружность» сначала делается замечание, что в отличие от треугольника около четырехугольника не всегда можно описать окружность. И далее приводится разъяснение: Например, нельзя описать окружность около ромба, не являющегося квадратом. Если же около четырехугольника можно описать окружность, то его углы обладают следующим свойством: В любом вписанном четырехугольнике сумма противоположных углов равна 180˚. Также верно и обратное утверждение: Если сумма противоположных углов четырехугольника равна 180˚, то около него можно описать окружность. Практический материал в данном учебнике содержится сразу же после изучаемого параграфа, что является очень удобным. Задачи в основном на вычисление площадей, периметров, также присутствуют задачи на построение. Как и в учебнике геометрии А. В. Атанасяна в учебнике под редакцией А. Д. Александрова нет отдельного параграфа. Параграф «Вписанные и описанные окружности» делится на несколько пунктов. В пункте «Окружность, описанная около многоугольника» говорится о том, что около многоугольника можно описать окружность, если найдется точка, равноудаленная от всех его вершин. Эта точка лежит на серединном перпендикуляре каждой стороны многоугольника. Следовательно, около многоугольника можно описать окружность тогда и только тогда, когда серединные перпендикуляры всех его сторон имеют общую точку. Около каждого треугольника можно описать окружность. Но не около каждого даже выпуклого четырехугольника можно описать окружность. Например, для параллелограмма это можно сделать лишь тогда, когда параллелограмм является прямоугольником. Остальные признаки и свойства предлагают вывести или доказать самостоятельно в задачах. Практический материал относится ко всему параграфу, а не разделен по пунктам. Все задачи разбиваются на ряд разделов, которые содержат задачи, дополняющие теорию, на вычисление, на доказательство, задачи на исследование и олимпиадные задачи. В учебнике под редакцией И. М. Смирновой о вписанных и описанных четырехугольниках говорится в главе VI «Многоугольники и окружность». Однако, в параграфе 36 «Многоугольники, вписанные в окружность» свойство вписанного четырехугольника вводят в качестве примера (условие задачи с решением): Докажите, что если около четырехугольника можно описать окружность, то сумма его противоположных углов равна 180˚. Решение: Пусть ABCD – четырехугольник, около которого описана окружность. Докажем, что B D 180 . Действительно, эти углы измеряются половинами соответствующих дуг ADC и ABC, которые вместе составляют всю окружность. Следовательно, сами углы в сумме измеряются половиной дуги окружности, т.е. их сумма равна 180˚. Некоторые свойства и признаки вписанных четырехугольников требуется вывести самостоятельно решая задачи, относящиеся к данному параграфу. Например, задача 11: Найдите диагональ прямоугольника, вписанного в окружность радиусом 6 см. Решение. Диагональ вписанного в окружность прямоугольника равна диаметру окружности (т.е. равна двум радиусам) т.е. 12 см. 13. Можно ли описать окружность около: а) прямоугольника; б) параллелограмма; в) ромба; г) квадрата; д) равнобедренной трапеции; е) прямоугольной трапеции? а) Можно, так как суммы противоположных углов равны; б) Нельзя, так как суммы противоположных углов не равны; в) Нельзя, так как суммы противоположных углов не равны; г) Около квадрата всегда можно описать, в квадрат всегда можно вписать окружность. Если сумма противоположных сторон четырехугольника равна сумме других противоположных сторон, то в него можно вписать окружность, а если суммы противоположных углов четырехугольника равны, около него можно описать окружность. Квадрат обладает и тем, и другим свойством. д) Около равнобедренной трапеции можно описать окружность, т.к. суммы противоположных углов равны. е) Около прямоугольной трапеции нельзя описать окружность. 18. Около трапеции описана окружность. Периметр трапеции равен 20 см, средняя линия 5 см. найдите боковые стороны трапеции. Решение. если около трапеции можно описать окружность то она равнобедренная. Пусть a, b - основания и c - боковая сторона. Тогда 2c+a+b=20, c+(a+b)/2=10. (a+b)/2 - средняя линия, которая равна 5, следовательно, боковые стороны равны с=10-5=5 см. В учебнике геометрия А. В. Погорелова такая тема как «Вписанные и описанные четырехугольники» не рассматривается, кроме вписанного квадрата, который рассматривается в параграфе 13 в качестве правильного многоугольника. Доказательства теорем в данных учебниках приводятся в готовом виде. Данные учебники имеют значительные различия. В учебнике под редакцией И. Ф. Шарыгина на изучение в 8 классе темы «Вписанные и описанные четырехугольники» отводится 4 часа. В учебнике Л. С. Атанасяна на изучение в 8 классе этой темы отводится всего лишь 2 часа. В учебниках А. Д. Александрова и И. М. Смирновой на изучение этой темы отводится также не более 3 часов. Практические задания темы «Вписанные и описанные четырехугольники», предлагаемые в учебниках И. М. Смирновой, Л. С. Атанасяна и И. Ф. Шарыгина, в отличие от учебников под редакцией А. В. Погорелова и А. Д. Александрова, располагаются в конце каждого пункта после изученного материала. В учебнике под редакцией Л. С. Атанасяна в конце главы имеется список заданий, предлагаемых с целью обобщения темы. Он включает задания повышенной сложности, а также интересные задания для детей, интересующихся математикой. Что касается оформления, то учебник под редакцией Л. С. Атанасяна отличается достаточной красочностью и количеством иллюстраций. Однако, сравнивая с учебником И. Ф. Шарыгина, чертежи в учебнике Л. С. Атанасяна меньшего масштаба, что порой доставляет неудобства. Проанализировав способы подачи материала в учебниках, можно сделать вывод, что учебники под редакцией И. М. Смирновой и А. Д. Александрова изучают рассматриваемые темы более глубоко, так как рассматривают материал более подробно, иногда выходя за рамки школьного курса геометрии, позволяя ученикам расширить свои знания геометрии, однако многие из них написаны непонятным для школьников языком, что вызывает затруднения при их изучении. Более легкая трактовка определений и доказательств теорем представлена в учебнике под редакцией И. Ф. Шарыгина. Материал усваивается легче, в сравнении с другими учебниками, в которых объем часов, отведенных на изучение данных тем, меньше, чем в учебнике И. Ф. Шарыгина. Глава 2. Методика изучения понятий вписанный и описанный четырёхугольник на основе выделения ключевых задач Ключевые задачи по теме вписанные и описанные четырёхугольники С помощью ключевых задач, акцентируется внимание на наиболее важных моментах изучениях темы, помогая ученикам не распылять своё внимание на менее важную информацию. Приведем некоторые ключевые задачи по теме вписанные четырёхугольники. Задача 1 [15]. Доказать, что: 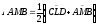 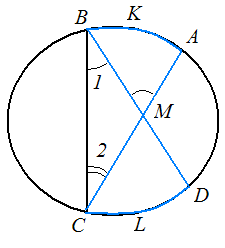 Решение: Проведем хорду ВС. Так как 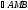 – внешний угол треугольника BMC, то – внешний угол треугольника BMC, то 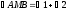 . По теореме о вписанном угле . По теореме о вписанном угле 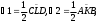 поэтому поэтому 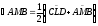 . .Задача 2 [15]. Доказать что четырёхугольник ABCD вписан в окружность тогда и только тогда, когда 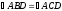 Решение: 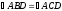 вписанные углы, опирающиеся на дугу AD. Около треугольника АВС можно описать окружность. На дуге ВС возьмем любую точку С. Получаем вписанный угол, опирающийся на дугу вписанные углы, опирающиеся на дугу AD. Около треугольника АВС можно описать окружность. На дуге ВС возьмем любую точку С. Получаем вписанный угол, опирающийся на дугу 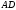 , который равен вписанному углу , который равен вписанному углу 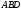 . .О  тсюда четырехугольник тсюда четырехугольник  – вписанный. – вписанный.Задача 3 [15]. Через точки А и В проведены прямые, перпендикулярные к сторонам угла АОВ и пересекающиеся в точке С внутри угла. Докажите, что около выпуклого четырёхугольника АВСО можно описать окружность. 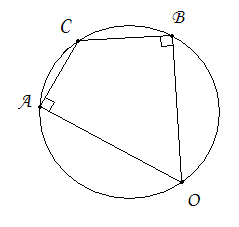 Решение: 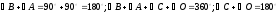 По свойству вписанного четырехугольника АВСО является вписанным. Задача 4 [15]. Д  окажите, что если около параллелограмма можно описать окружность, то этот параллелограмм – прямоугольник. окажите, что если около параллелограмма можно описать окружность, то этот параллелограмм – прямоугольник.Решение: Допустим обратное. Необязательно параллелограмм прямоугольник. Значит, какие то противолежащие углы в сумме дают меньше 180˚. Пусть это будут углы В иD. 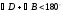 Так как параллелограмм вписанный: 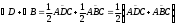 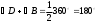 Противоречие. Аналогично, если вместо данных углов брать углы А и С. Значит, параллелограмм прямоугольный. Что и требовалось доказать. Задача 5 [15]. Докажите, что если ромб можно вписать в окружность, то этот ромб – квадрат.  Решение: Допустим обратное. Этот ромб не является квадратом, но, тем не менее, вписан в окружность. Т. е. углы не равны 90. Значит: 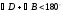 . . Так как ромб вписанный: 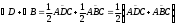 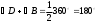 Противоречие. Аналогично, если вместо данных углов брать углы А и С. Значит, стороны ромба равны 90˚. У ромба все стороны равны. Значит, ромб является квадратом. Задача 6 [15]. Докажите, что около выпуклого четырехугольника, образованного при пересечении биссектрис углов трапеции можно описать окружность. 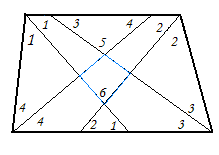 Решение: Из предыдущих задач нам известно, что если противоположные углы в сумме дают 180˚, то четырёхугольник можно вписать. Докажем, что в данном четырёхугольнике углы дают в сумме 180˚. 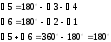 Рассмотрим ключевые задачи, связанные с описанными четырехугольниками. Задача 7 [16]. Докажите, что у четырёхугольника, описанного около окружности, суммы противоположных сторон равны. Решение Отрезки касательных, проведённых из одной точки к окружности, равны между собой. Точки касания делят каждую сторону четырёхугольника на две части. Обозначим последовательно их длины, используя одну букву для равных отрезков, начиная от какой-нибудь из вершин: a, b, b, c, c, d, d, a. Ясно, что суммы противоположных сторон состоят из одинаковых слагаемых. 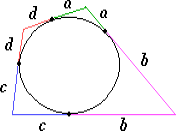 Задача 8 [16]. Докажите, что во всяком описанном четырёхугольнике середины диагоналей и центр вписанной окружности расположены на одной прямой. Пусть ABCD – описанный четырёхугольник, O – центр вписанной окружности, r –её радиус, N и K – середины диагоналей AC и BD соответственно. Если ABCD – ромб, то все эти точки совпадают. В противном случае можно считать, что стороны AB и CD не параллельны. Заметим, что SANB + SDNC = ½ SABC + ½ SADC = ½ SABCD. Аналогично, SAKB + SDKC =½ SABCD. Пусть P и L – точки касания вписанной окружности со сторонами AB и CD. Тогда SAOB + SCOD = ½ AB·OP + ½ CD·OL = ½ r(AB + CD) = ½ r(AD + BC). Поэтому SAOB + SCOD = ½ SABCD. Точки N, O и K лежат на одной прямой. 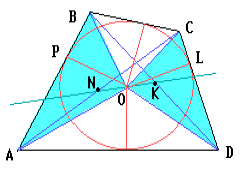 Задача 9 [16]. Доказать, что если окружность касается трёх сторон выпуклого четырёхугольника и не пересекает четвёртой, то сумма четвёртой и противоположной ей стороны меньше суммы остальных сторон четырёхугольника. Решение: Проведем из точки C касательную к окружности (рис.). Получили описанный четырехугольник. 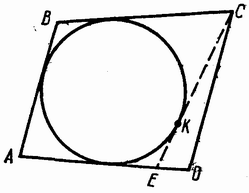 Суммы противоположных сторон его равны: BC+AE=AB+CE . Сумма противоположных сторон четырехугольника BC+AD=BC+AE+ED=(BC+AE)+ED. Подставим значение BC+AE из первого равенства: BC+AD=(AB+CE)+ED=AB+(CE+ED). Из треугольника ECD : CE+ED>CD , поэтому AB+(CE+ED)>AB+CD . Таким образом, BC+AD>AB+CD . Задача 10 [16]. Отрезок AB пересекает две равные окружности и параллелен их линии центров, причём все точки пересечения прямой AB с окружностями лежат между A и B. Через точку A проводятся касательные к окружности, ближайшей к A, через точку B – касательные к окружности, ближайшей к B. Оказалось, что эти четыре касательные образуют четырёхугольник, содержащий внутри себя обе окружности. Докажите, что в этот четырёхугольник можно вписать окружность. Решение: Пусть касательные образуют четырёхугольник ACBD. Обозначим через O1 и O2 центры окружностей. Сдвинем правую часть картинки влево параллельно линии центров на расстояние O1O2. При этом окружности совпадут, а касательные, проведённые из точки B, перейдут в касательные, проведённые из точки B', лежащей на прямой AB (см. рис.). Гомотетия с центром A и коэффициентом AD : AB' переводит точку B', в B, а прямую B'K – в параллельную ей прямую BD. Аналогично она переводит прямую B'L в BC. Поскольку прямые AD и AC переходят в себя, четырёхугольник AKB'L перейдёт в исходный четырёхугольник ADBC. Но четырёхугольник AKB'L – описанный. Значит, и четырёхугольник ADBC тоже описанный. 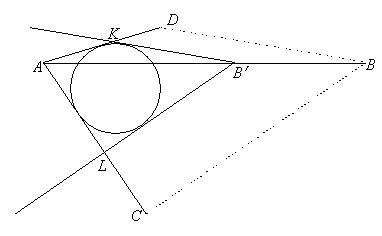 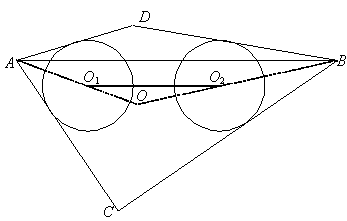 Данные задачи можно считать ключевыми, так как для их решения используется наибольшее количество материала по теме, что позволяет ученику более глубоко усваивать пройденный материал, и применять его на практике для решения более сложных задач. |
