Проверено 8.11.2020 Курсовая. Задача 8 3 Анализ содержания темы Вписанные и описанные четырёхугольники
 Скачать 0.7 Mb. Скачать 0.7 Mb.
|
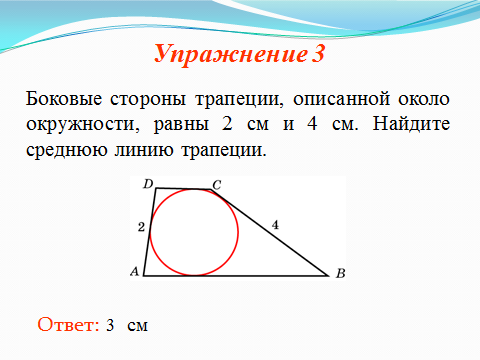
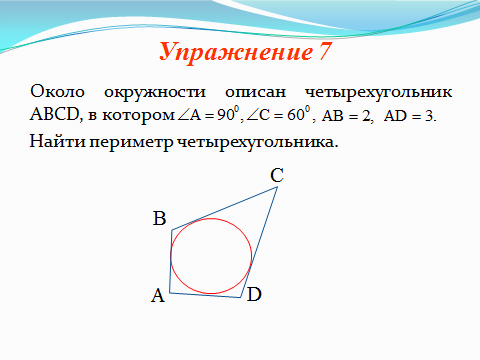
2.2 Методические рекомендации по изучению понятия вписанный четырёхугольникЦель урока: Дидактическая: сформулировать понятие и свойства вписанного четырехугольника; сформировать навыки применения полученных знаний по теме при решении задач. Для работы на уроке нам нужно повторить виды четырехугольников. Задание: Вспомните определения всех четырёхугольников и распределите названия фигур по местам. Помните: у одной фигуры может быть несколько названий. Четырёхугольник, трапеция . Четырёхугольник. Четырёхугольник, прямоугольник, параллелограмм, ромб, квадрат. Четырёхугольник, параллелограмм, ромб. Четырёхугольник, прямоугольник, параллелограмм. Четырёхугольник, параллелограмм. Сначала ученики по одному рассказывают определения каждого из четырехугольников, тем самым концентрируя внимание только на них. Далее учитель показывает на определенную фигуру, а ученики называют её исходя из приведенных ранее определений. Отметим на окружности четыре точки, и соединим их хордами. Получили четырехугольник, вписанный в окружность.  - попробуйте сформулировать определение вписанного четырехугольника. (Четырехугольник, все вершины которого лежат на окружности, называется вписанным в эту окружность, а окружность – описанной.) На другой окружности отметим 4 точки и проведем через них отрезки касательных. Получили четырехугольник, описанный около окружности. - попробуйте сформулировать определение описанного четырехугольника. (Четырехугольник, все стороны которого касаются окружности, называется описанным около этой окружности. А окружность – вписанной в этот четырехугольник.)  Свойства вписанного четырехугольника и его признак связаны с углами этого четырехугольника. Теорема (свойство углов вписанного четырехугольника) Сумма противоположных углов вписанного четырехугольника равна 180°. 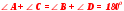 - всегда ли можно вписать четырехугольник в окружность? (нет) - попробуйте сформулируйте теорему обратную? Если …., то… Это будет признаком вписанного четырехугольника Если в четырехугольнике сумма двух противоположных углов равна 180°, то около такого четырехугольника можно описать окружность. Для доказательства теоремы нужно повторить понятие вписанного четырехугольника, а также признаки вписанного четырехугольника. Пусть в окружность с центром О вписан четырёхугольник ABCD. Требуется доказать, что / А + / С = 180° и / В + / D = 180°. / А, как вписанный в окружность О, измеряется 1/2 / С, как вписанный в ту же окружность, измеряется 1/2 Следовательно, сумма углов А и С измеряется полусуммой дуг BCD и BAD в сумме же эти дуги составляют окружность, т. е. имеют 360°. Отсюда / А + / С = 360° : 2 = 180°. Аналогично доказывается, что и / В + / D = 180°. Однако это можно вывести и иным путём. Так как известно, что сумма внутренних углов выпуклого четырёхугольника равна 360°. Сумма углов А и С равна 180°, значит, на сумму других двух углов четырёхугольника остаётся тоже 180° . Для закрепления материала можно сделать следующие задачи: Задача 1. Доказать, что для равнобедренной трапеции ABCD (АВ=CD) справедливо равенство 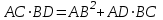 (Устно, по готовому чертежу) (Устно, по готовому чертежу)Д 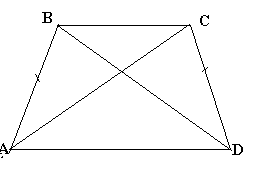 ано: ано:ABCD-трапеция АВ=CD Доказать: Доказательство: Какое свойство можно использовать при доказательстве? Ответ. 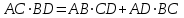 Что следует из этого свойства? АВ=CD, значит 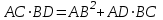 Что и т.д. Что и т.д.Задача 2. На окружности, описанной около равностороннего треугольника АВС взята точка Е, отличная от вершин треугольника. Доказать, что один из отрезков АЕ, ЕВ, ЕС равен сумме двух других. Д 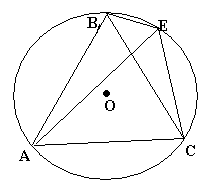 ано: ано: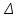 АВС АВС АВ=ВС=СА Точка Е лежит на Окр(О;R) Доказать: АЕ=ВЕ+ЕС Доказательство: Можно ли воспользоваться ранее изученным свойством? Данное свойство применимо к задаче Что следует из этого свойства? АВ=ВС=СА, то 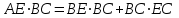 , откуда АЕ=ВЕ+ЕС. Что и т.д. , откуда АЕ=ВЕ+ЕС. Что и т.д.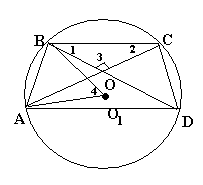 Задача 3. Дано: ABCD – трапеция Окр(О1,R)- описанная около трапеции АС  ВD ВDДоказать: 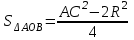 Доказательство. Что можно заметить из условия задачи?  1 = 1 = 2= 2=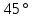 , тогда , тогда 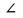 4= 4=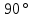 . . Какое свойство подходит для доказательства? 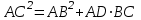 ; ;Какие выводы следуют из этого свойства? 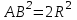 , , 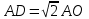 , значит , значит 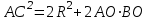 , откуда , откуда 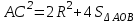 и и 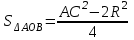 . Что и т.д. . Что и т.д.Методические рекомендации по изучению понятия описанный четырёхугольник Тема: Описанные четырехугольники Цели на урок: ввести понятие описанного многоугольника, ознакомить учащихся со свойствами описанного четырехугольника. II.Актуализация знаний. Математический диктант. Можно ли описать окружность около параллелограмма? Прямоугольника? Ромба? Почему? Может ли вписанный в окружность четырехугольник иметь равные стороны, но неравные углы? Почему? Может ли вписанный в окружность многоугольник иметь равные углы, но неравные стороны? Почему? Можно ли описать окружность около пятиугольника с углами 800, 900, 1000, 1300, 1400? Почему? Какой четырехугольник называется дельтоидом? Перечислите его свойства. Для нахождения ответов на поставленные вопросы можно провести диалог между учителем и учеником. Чтобы ответить на вопросы, нужно повторить ранее изученные определения, а именно, определения вписанного и описанного четырехугольника, свойства вписанных и описанных четырехугольников. Устная работа Внимательно рассмотрите рисунки. Как вы думаете, какие многоугольники являются описанными около окружности. Почему вы так решили? Как можно назвать стороны этих четырехугольников по отношению к окружности? 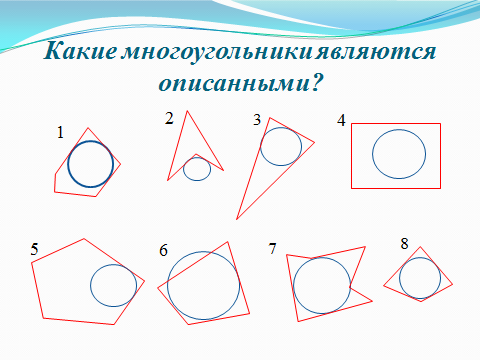 Попробуйте сформулировать определение описанного многоугольника 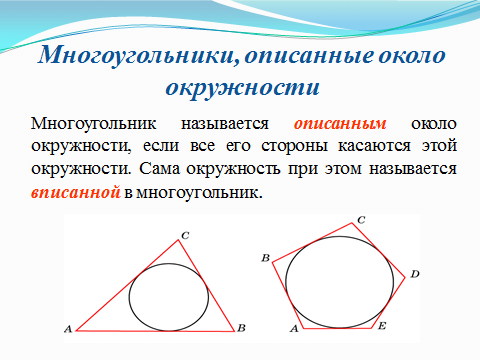 III.Учебно-познавательная деятельность. Перейдем теперь к рассмотрению описанных многоугольников. Ситуация здесь в некотором смысле двойственная по отношению к вписанным многоугольникам. При этом стороны описанного многоугольника двойственны углам вписанного многоугольника. Так, например, если для вписанного четырехугольника необходимым и достаточным условием является равенство сумм противолежащих углов, то для описанного выпуклого четырехугольника необходимым и достаточным условием является равенство сумм противоположных сторон. А именно, имеют место следующие теоремы. Теорема 1 (свойство сторон описанного четырехугольника) Суммы противоположных сторон описанного около окружности четырехугольника равны. 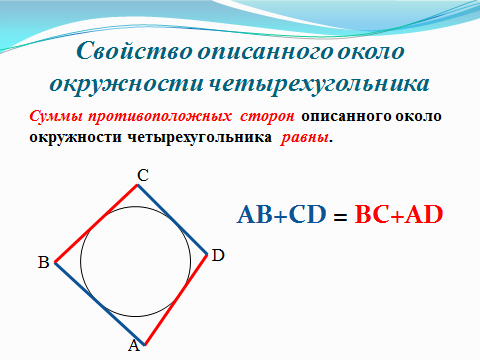 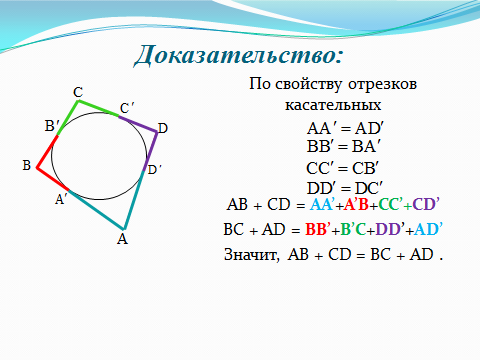 Теорема 2 (признак четырехугольника, в который можно вписать окружность) Если суммы противоположных сторон выпуклого четырехугольника равны, то в него можно вписать окружность. Учащимся предлагается самостоятельно разобрать доказательство по учебнику (работа с учебником в течение 5 минут, после чего учащиеся могут задавать вопросы по доказательству). 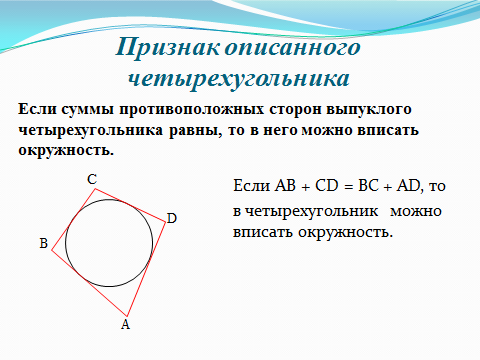 Замечание: в процессе разбора доказательства теорем группа учащихся, самостоятельно разбиравших дома теоремы и готовивших слайды к презентации выполняют индивидуальные задания. Каждому ученику выдаётся карточка с планом исследования . Выполняя задания в соответствии с этим планом, ученики все промежуточные действия и конечные выводы записывают в тетрадях. (Приложение 2) IV. Решение задач. Устная работа Можно ли вписать окружность в прямоугольник? Можно ли вписать окружность в квадрат? Можно ли вписать окружность в ромб? Можно ли вписать окружность в параллелограмм? В какие ещё четырехугольники можно вписать окружность? При каком условии можно вписать окружность в трапецию? Задачи слайдов 7 – 11.
Раздается таблица «Примеры описанных четырехугольников» Письменная работа(решение задач по готовым чертежам (слайды 12 – 13))
Заключение В ходе выполнения работы по рассмотрению темы «Ключевые задачи по теме вписанные и описанные четырехугольники» были получены следующие результаты: Выделены основные теоретические аспекты подходов к изучению математических понятий; Проведен анализ понятия «Ключевая задача» Рассмотрен анализ содержания темы «Вписанные и описанные четырехугольники» Выделены базовые ключевые задачи по теме «Вписанные и описанные четырехугольники» Даны фрагменты уроков по темам «Вписанные и описанные четырехугольники» Вписанные и описанные четырехугольники являются одной из ключевых тем в основном курсе геометрии, поэтому роль ключевых задач при изучении является весь существенной. Также ключевые задачи помогают бороться с проблемой полезависимости учащихся, которая часто только мешает развиваться в изучении различного материала. Список использованной литературы Александров, А. Д. Геометрия [Текст] : учеб. пособие для 9 кл. с углубл. изучением математики / А. Д. Александров, А. Л. Вернер, В. И. Рыжик. – Москва : Просвещение, 2016. – 240 с. Алябьева В. Г. «Многообразие конфигураций: от геометрических до тактических. исторический очерк» [Текст]// Пермский государственный национальный исследовательский университет// г. Пермь – 2013. Аргунов Б. И. и Скорняков Л. А. «Конфигурационные теоремы» [Текст] // Государственное издательство технико-теоретической литературы// г. Москва - 1957. Атанасян, Л. С. Геометрия. 7-9 классы [Текст] : учеб. для общеобразоват. учреждений / Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев и др. – 20-е изд. – Москва : Просвещение, 2016. – 384 с. Э.Н.Балаян «Геометрия: задачи на готовых чертежах 7-9 классы»…. Бурмистрова, Т. А. Геометрия. Сборник рабочих программ. 7 – 9 классы [Текст] : пособие для учителей общеобразов. организаций / [сост. Т. А. Бурмистрова]. – 2-е изд., дораб. – Москва : Просвещение, 2014. – 95 с. Виленкин Н.Я., Абайдулин С.К., Таварткиладзе Р.К. Определения в школьном курсе математики и методика работы над ними //Математика в школе. – 2014. -№4 Груденов Я.И. Изучение определений, аксиом и теорем. – М, 2011. Гусев, В. А. Методика обучения геометрии: учеб. пособие для студ. высш. пед. учеб. заведений [Текст] / В. А. Гусев, В. В. Орлов, В. А. Панчищина и др.; под ред. В. А. Гусева. – Москва : Издат. центр «Академия», 2004. – 368 с. Дорофеев Г.В. О строгости определения математических понятий школьного курса с методической точки зрения // Математика в школе. – 2009. -№ 3 Гусев, В. А. Развитие пространственного мышления учащихся как одна из основных задач школьного математического образования [Текст] / В. А. Гусев // Школа будущего. – 2013. – № 3. – С. 65-70. Жук, Л. В. Реализация дидактического принципа наглядности в обучении геометрии средствами информационных компьютерных технологий [Текст] / Л. В. Жук // European Social Science Journal. – 2014. – № 4-1 (43). – С. 157-160. Звавич, Л. И. Тесты по геометрии. 8 класс: к учебнику Л. С. Атанасяна, В. Ф. Бутузова, С. Б. Кадомцева и др. «Геометрия. 7-9 классы» [Текст] / Л. И. Звавич, Е. В. Потоскуев. – Москва : Издательство «Экзамен», 2013. – 158 с. Зильберберг Н.И. Урок математики: подготовка и проведение [Текст] // Н.И.Зильберберг. -М.: Просвещение, 1996. - 176 с. Каталог заданий. Задача на доказательство и вычисление [Электронный ресурс] // Образовательный портал для подготовки к экзаменам «Решу ЕГЭ». – Режим доступа : https://ege.sdamgia.ru/test?theme=206. Каталог заданий. Задача на доказательство и вычисление [Электронный ресурс] //Интернет-проект «Задачи».– Режим доступа : http://www.problems.ru/about_system.php Лоповок Л.М. «Факультативные задания по геометрии для 7-11 классов. Пособие для учителя» [Текст]// г.Киев, «РАДЯНСЬКА ШКОЛА». – 1990. – C.23. Мищенко, Т. М. Дидактические материалы и методические рекомендации для учителя по геометрии: 9 класс : к учебнику Ф .В. Погорелова «Геометрия. 7-9 классы». ФГОС (к новому учебнику) [Текст] / Т. М. Мищенко. – Москва : Издательство «Экзамен», 2015. – 225 с. Мордковича А.Г. «Беседы с учителями математики»…. Погорелов, А. В. Геометрия. 7–9 классы [Текст] : учеб. для общеобразоват. организаций / А. В. Погорелов. – 2-е изд. – Москва: Просвещение, 2014. – 240 с. Прасолов В.В. «Задачи по планиметрии»./ Учебное пособие, 6-е издание./ Издательство МЦНМО// г.Москва – 2007. C.11-16. Примерная основная образовательная программа основного общего образования. Одобрена решением федерального учебно-методического объединения по общему образованию [Текст] / М-во образования и науки РФ. – Москва : Просвещение, 2015. – 560 с. Саранцев, Г. И. Общая методика преподавания математики [Текст] : учеб. пособие для студентов мат. спец. пед. вузов и университетов / Г. И. Саранцев. – Саранск : Тип. «Крас. Окт.», 1999. – 208 с. Смирновой И. М. «Геометрия 7 - 9» [Текст] / И. М. Смирнова, В. А. Смирнов. – Москва : МЦНМО, 2015. – 2-е изд., доп. – 216 с. Шарыгин, И. Ф. Геометрия. 7-9 кл. [Текст] : учеб. для общеобразоват. учреждений / И. Ф. Шарыгин. – Москва : Дрофа, 2012. – 462 с. Шарыгин И.Ф. «Нужна ли школе 21 века геометрия?» [Текст]:серия 3,8 – Москва: Изд-во МЦНМО, 2004, с. 37-52. Шарыгин, И.Ф. Рассуждения о концепции школьной геометрии [Текст] / И.Ф.Шарыгин. - М.: МЦНМО, 2000 - 56 с. 48 Шарыгин, И.Ф. Решение задач: Учебное пособие для 10 класса общеобразовательных учреждений [Текст] / И.Ф.Шарыгин. - М.: Просвещение, 1994.-252 с. 192-195 Ященко И.В., Рослова Л.О., Высоцкий И.Р., Семенов А.В. «Методические рекомендации для учителей, подготовленные на основе анализа типичных ошибок участников ЕГЭ 2018 года по МАТЕМАТИКЕ» [Текст] // Москва – 2018. | ||||||||||