Задача 8 в таблице приведены работы, выполняемые при строительстве нового каркасного дома. Работа

• Название: Задача 8 в таблице приведены работы, выполняемые при строительстве нового каркасного дома. Работа
• Дата: 01.12.2021
• Размер: 74 Kb.
• Имя файла: PRZ 6.docx
• Тип: Задача; #288430

Тема №6 «Метод критической цепи»
Задача 8

В таблице приведены работы, выполняемые при строительстве нового каркасного дома.

Работа	Предшествующие работы	Длительность (дни)
A - Очистка строительного участка	–	1
B - Завоз оборудования	–	2
C - Земляные работы	А	1
D - Заливка фундамента	С	2
E - Наружные сантехнические работы	В,	6
F - Возведение каркаса дома	D	10
G - Прокладка электропроводки	F	3
H - Создание перекрытий	G	1
I - Создание каркаса крыши	F	1
J - Внутренние сантехнические работы	Е,	5
K - Покрытие крыши	I	2
L - Наружные изоляционные работы	F,	1
M - Вставка окон и наружных дверей	F	2
N - Обкладка дома кирпичом	L	4
O - Штукатурка стен и потолков	G	2
P - Облицовка стен и потолков	О	2
Q - Изоляция крыши	I	1
R - Окончание внутренних отделочных работ	Р	7
S - Окончание наружных отделочных работ	I	7
T - Ландшафтные работы	S	3

Вопросы:

• 
  Сколько работ находится на критическом пути (фиктивные работы не учитываются)?
  
• 
  Через какое минимальное время после принятия решения о реализации проекта можно начать работу по строительству библиотеки?
  
• 
  На сколько недель можно отложить выбор архитектурной мастерской?
  
• 
  Важнейшим показателем сетевого графика являются резервы времени. Резервы времени каждого пути показывают, насколько может быть увеличена продолжительность данного пути без ущерба для наступления завершающего события. Поскольку каждый некритический путь сетевого графика имеет свой полный резерв времени, то и каждое событие этого пути имеет свой резерв времени.
  

  Элемент сети	Наименование параметра	Условное обозначение параметра
  Событие i	Ранний срок свершения события	tp(i)
  	Поздний срок свершения события	t(i)
  	Резерв времени события	R(i)
  Работа (i, j)	Продолжительность работы	t(i,j)
  	Ранний срок начала работы	tрн(i,j)
  	Ранний срок окончания работы	tpo(i,j)
  	Поздний срок начала работы	tпн(i,j)
  	Поздний срок окончания работы	tпо(i,j)
  	Полный резерв времени работы	Rп(i,j)
  Путь L	Продолжительность пути	t(L)
  	Продолжительность критического пути	tkp
  	Резерв времени пути	R(L)

• 
  Резерв времени события показывает, на какой допустимый период времени можно задержать наступление этого события, не вызывая при этом увеличения срока выполнения комплекса работ.
  
• 
  Для определения резервов времени по событиям сети рассчитывают наиболее ранние t^p и наиболее поздние t^п сроки свершения событий. Любое событие не может наступить прежде, чем свершаться все предшествующие ему события и не будут выполнены все предшествующие работы. Поэтому ранний (или ожидаемый) срок tp(i) свершения i-ого события определяется продолжительностью максимального пути, предшествующего этому событию:
  
• 
  t^p(i) = max(t(L_ni))
  
• 
  где L_ni – любой путь, предшествующий i-ому событию, то есть путь от исходного до i-ого события сети.
  
• 
  Если событие j имеет несколько предшествующих путей, а следовательно, несколько предшествующих событий i, то ранний срок свершения события j удобно находить по формуле:
  
• 
  t^p(j) = max[t^p(i) + t(i,j)]
  
• 
  Задержка свершения события i по отношению к своему раннему сроку не отразится на сроке свершения завершающего события (а значит, и на сроке выполнения комплекса работ) до тех пор, пока сумма срока свершения этого события и продолжительности (длины) максимального из следующих за ним путей не превысит длины критического пути. Поэтому поздний (или предельный) срок t^п(i) свершения i-ого события равен:
  
• 
  t^п(i) = t_kp - max(t(L_ci))
  
• 
  где L_ci - любой путь, следующий за i-ым событием, т.е. путь от i-ого до завершающего события сети.
  
• 
  Составим сетевой график: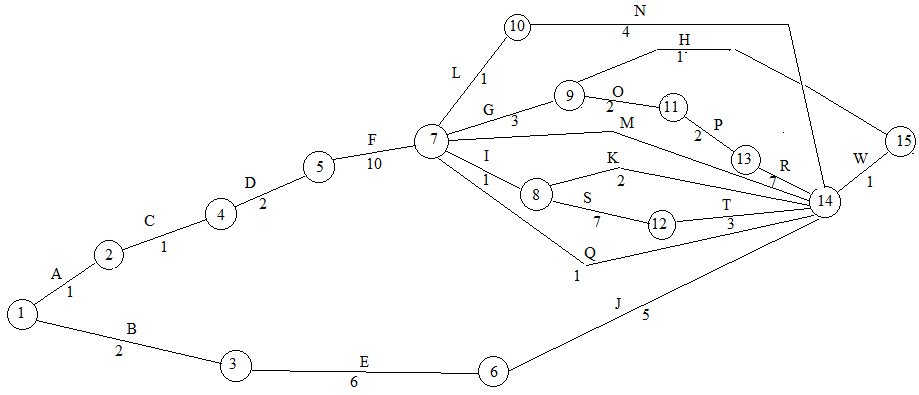
  
• 
  
  
• 
  
  
• 
  Если событие i имеет несколько последующих путей, а следовательно, несколько последующих событий j, то поздний срок свершения события i удобно находить по формуле:
  
• 
  t^п(i) = min[t^п(j) - t(i,j)]
  
• 
  Резерв времени R(i) i-ого события определяется как разность между поздним и ранним сроками его свершения:
  
• 
  R(i) = t^п(i) - t^p(i)
  
• 
  Резерв времени события показывает, на какой допустимый период времени можно задержать наступление этого события, не вызывая при этом увеличения срока выполнения комплекса работ.
  
• 
  Критические события резервов времени не имеют, так как любая задержка в свершении события, лежащего на критическом пути, вызовет такую же задержку в свершении завершающего события. Таким образом, определив ранний срок наступления завершающего события сети, мы тем самым определяем длину критического пути.
  
• 
  Расчет сроков свершения событий.
  
• 
  Для i=1 (начального события), очевидно tp(1)=0.
  
• 
  i=2: t^p(2) = t^p(1) + t(1,2) = 0 + 1 = 1.
  
• 
  i=3: t^p(3) = t^p(1) + t(1,3) = 0 + 2 = 2.
  
• 
  i=4: t^p(4) = t^p(2) + t(2,4) = 1 + 1 = 2.
  
• 
  i=5: t^p(5) = t^p(4) + t(4,5) = 2 + 2 = 4.
  
• 
  i=6: t^p(6) = t^p(3) + t(3,6) = 2 + 6 = 8.
  
• 
  i=7: t^p(7) = t^p(5) + t(5,7) = 4 + 10 = 14.
  
• 
  i=8: t^p(8) = t^p(7) + t(7,8) = 14 + 1 = 15.
  
• 
  i=9: t^p(9) = t^p(7) + t(7,9) = 14 + 3 = 17.
  
• 
  i=10: t^p(10) = t^p(7) + t(7,10) = 14 + 1 = 15.
  
• 
  i=11: t^p(11) = t^p(9) + t(9,11) = 17 + 2 = 19.
  
• 
  i=12: t^p(12) = t^p(8) + t(8,12) = 15 + 7 = 22.
  
• 
  i=13: t^p(13) = t^p(11) + t(11,13) = 19 + 2 = 21.
  
• 
  i=14: max(t^p(6) + t(6,14);t^p(7) + t(7,14);t^p(8) + t(8,14);t^p(10) + t(10,14);t^p(12)
  
• 
  + t(12,14);t^p(13) + t(13,14)) = max(8 + 5;14 + 2;15 + 2;15 + 4;22 + 3;21 + 7) = 28.
  
• 
  i=15: max(t^p(9) + t(9,15);t^p(14) + t(14,15)) = max(17 + 1;28 + 1) = 29.
  
• 
  Длина критического пути равна раннему сроку свершения завершающего события 15: t_kp=tp(15)=29
  
• 
  При определении поздних сроков свершения событий t_п(i) двигаемся по сети в обратном направлении, то есть справа налево.
  
• 
  Для i=15 (завершающего события) поздний срок свершения события должен равняться его раннему сроку (иначе изменится длина критического пути): t^п(15)= t^р(15)=29
  
• 
  Далее просматриваются строки, оканчивающиеся на номер предпоследнего события, т.е. 14. Просматриваются все строчки, начинающиеся с номера 14.
  
• 
  i=14: t^п(14) = t^п(15) - t(14,15) = 29 - 1 = 28.
  
• 
  Далее просматриваются строки, оканчивающиеся на номер предпоследнего события, т.е. 14. Просматриваются все строчки, начинающиеся с номера 14.
  
• 
  i=14: t^п(14) = t^п(15) - t(14,15) = 29 - 1 = 28.
  
• 
  Далее просматриваются строки, оканчивающиеся на номер предпоследнего события, т.е. 13. Просматриваются все строчки, начинающиеся с номера 13.
  
• 
  i=13: t^п(13) = t^п(14) - t(13,14) = 28 - 7 = 21.
  
• 
  Далее просматриваются строки, оканчивающиеся на номер предпоследнего события, т.е. 14. Просматриваются все строчки, начинающиеся с номера 14.
  
• 
  i=14: t^п(14) = t^п(15) - t(14,15) = 29 - 1 = 28.
  
• 
  Далее просматриваются строки, оканчивающиеся на номер предпоследнего события, т.е. 11. Просматриваются все строчки, начинающиеся с номера 11.
  
• 
  i=11: t^п(11) = t^п(13) - t(11,13) = 21 - 2 = 19.
  
• 
  Далее просматриваются строки, оканчивающиеся на номер предпоследнего события, т.е. 14. Просматриваются все строчки, начинающиеся с номера 14.
  
• 
  i=14: t^п(14) = t^п(15) - t(14,15) = 29 - 1 = 28.
  
• 
  Далее просматриваются строки, оканчивающиеся на номер предпоследнего события, т.е. 12. Просматриваются все строчки, начинающиеся с номера 12.
  
• 
  i=12: t^п(12) = t^п(14) - t(12,14) = 28 - 3 = 25.
  
• 
  Далее просматриваются строки, оканчивающиеся на номер предпоследнего события, т.е. 14. Просматриваются все строчки, начинающиеся с номера 14.
  
• 
  i=14: t^п(14) = t^п(15) - t(14,15) = 29 - 1 = 28.
  
• 
  Далее просматриваются строки, оканчивающиеся на номер предпоследнего события, т.е. 10. Просматриваются все строчки, начинающиеся с номера 10.
  
• 
  i=10: t^п(10) = t^п(14) - t(10,14) = 28 - 4 = 24.
  
• 
  Далее просматриваются строки, оканчивающиеся на номер предпоследнего события, т.е. 9. Просматриваются все строчки, начинающиеся с номера 9.
  
• 
  i=9: min(t^п(11) - t(9,11);t^п(15) - t(9,15)) = min(19 - 2;29 - 1) = 17.
  
• 
  Далее просматриваются строки, оканчивающиеся на номер предпоследнего события, т.е. 8. Просматриваются все строчки, начинающиеся с номера 8.
  
• 
  i=8: min(t^п(12) - t(8,12);t^п(14) - t(8,14)) = min(25 - 7;28 - 2) = 18.
  
• 
  Далее просматриваются строки, оканчивающиеся на номер предпоследнего события, т.е. 14. Просматриваются все строчки, начинающиеся с номера 14.
  
• 
  i=14: t^п(14) = t^п(15) - t(14,15) = 29 - 1 = 28.
  
• 
  Далее просматриваются строки, оканчивающиеся на номер предпоследнего события, т.е. 7. Просматриваются все строчки, начинающиеся с номера 7.
  
• 
  i=7: min(t^п(8) - t(7,8);t^п(9) - t(7,9);t^п(10) - t(7,10);t^п(14) - t(7,14)) = min(18 - 1;17 - 3;24 - 1;28 - 2) = 14.
  
• 
  Далее просматриваются строки, оканчивающиеся на номер предпоследнего события, т.е. 5. Просматриваются все строчки, начинающиеся с номера 5.
  
• 
  i=5: t^п(5) = t^п(7) - t(5,7) = 14 - 10 = 4.
  
• 
  Далее просматриваются строки, оканчивающиеся на номер предпоследнего события, т.е. 6. Просматриваются все строчки, начинающиеся с номера 6.
  
• 
  i=6: t^п(6) = t^п(14) - t(6,14) = 28 - 5 = 23.
  
• 
  Далее просматриваются строки, оканчивающиеся на номер предпоследнего события, т.е. 4. Просматриваются все строчки, начинающиеся с номера 4.
  
• 
  i=4: t^п(4) = t^п(5) - t(4,5) = 4 - 2 = 2.
  
• 
  Далее просматриваются строки, оканчивающиеся на номер предпоследнего события, т.е. 3. Просматриваются все строчки, начинающиеся с номера 3.
  
• 
  i=3: t^п(3) = t^п(6) - t(3,6) = 23 - 6 = 17.
  
• 
  Далее просматриваются строки, оканчивающиеся на номер предпоследнего события, т.е. 2. Просматриваются все строчки, начинающиеся с номера 2.
  
• 
  i=2: t^п(2) = t^п(4) - t(2,4) = 2 - 1 = 1.
  
• 
  Далее просматриваются строки, оканчивающиеся на номер предпоследнего события, т.е. 1. Просматриваются все строчки, начинающиеся с номера 1.
  
• 
  i=1: min(t^п(2) - t(1,2);t^п(3) - t(1,3)) = min(1 - 1;17 - 2) = 0.
  
• 
  
  
• 
  
  
• 
  
  
• 
  
  
• 
  
  
• 
  
  
• 
  Таблица 1 - Расчет резерва событий
  

  Номер события	Сроки свершения события: ранний tp(i)	Сроки свершения события: поздний tп(i)	Резерв времени, R(i)
  1	0	0	0
  2	1	1	0
  3	2	17	15
  4	2	2	0
  5	4	4	0
  6	8	23	15
  7	14	14	0
  8	15	18	3
  9	17	17	0
  10	15	24	9
  11	19	19	0
  12	22	25	3
  13	21	21	0
  14	28	28	0
  15	29	29	0

• 
  Следует отметить, что кроме полного резерва времени работы, выделяют еще три разновидности резервов. Частный резерв времени первого вида R₁ - часть полного резерва времени, на которую можно увеличить продолжительность работы, не изменив при этом позднего срока ее начального события. R₁ находится по формуле:
  
• 
  R(i,j)= R^п(i,j) - R(i)
  
• 
  Частный резерв времени второго вида, или свободный резерв времени Rc работы (i,j) представляет собой часть полного резерва времени, на которую можно увеличить продолжительность работы, не изменив при этом раннего срока ее конечного события. Rc находится по формуле:
  
• 
  R(i,j)= R^п(i,j) - R(j)
  
• 
  Значение свободного резерва времени работы указывает на расположение резервов, необходимых для оптимизации.
  
• 
  
  
• 
  
  
• 
  
  
• 
  
  

  Работа (i,j)	Продолжительность tij	Потенциал события TiП	Раннее начало работ TijРН	Ранее окончание работ TijРО	Позднее начало работ TijПН	Позднее окончание работ TijПО	Общий резерв времени RijO	Частный резерв времени RijЧ
  (1,2)	1	29	0	1	0	0	0	0
  (1,3)	2	29	0	2	15	0	15	15
  (2,4)	1	28	1	2	1	1	0	0
  (3,6)	6	12	2	8	17	17	15	0
  (4,5)	2	27	2	4	2	2	0	0
  (5,7)	10	25	4	14	4	4	0	0
  (6,14)	5	6	8	13	23	23	15	0
  (7,8)	1	15	14	15	17	14	3	3
  (7,9)	3	15	14	17	14	14	0	0
  (7,10)	1	15	14	15	23	14	9	9
  (7,14)	2	15	14	16	26	14	12	12
  (8,12)	7	11	15	22	18	18	3	0
  (8,14)	2	11	15	17	26	18	11	8
  (9,11)	2	12	17	19	17	17	0	0
  (9,15)	1	12	17	18	28	17	11	11
  (10,14)	4	5	15	19	24	24	9	0
  (11,13)	2	10	19	21	19	19	0	0
  (12,14)	3	4	22	25	25	25	3	0
  (13,14)	7	8	21	28	21	21	0	0
  (14,15)	1	1	28	29	28	28	0	0

• 
  Независимый резерв времени Rн работы (i,j) - часть полного резерва, получаемая для случая, когда все предшествующие работы заканчиваются в поздние сроки, а все последующие начинаются в ранние сроки. Rн находится по формуле:
  
• 
  R(i,j)= R^п(i,j)- R(i) - R(j)
  
• 
  Критический путь: (1,2)(2,4)(4,5)(5,7)(7,9)(9,11)(11,13)(13,14)(14,15)
  
• 
  Продолжительность критического пути: 29
  
• 
  
  
• 
  
  
• 
  
  
• 
  
  
• 
  
  
• 
  Карта проекта: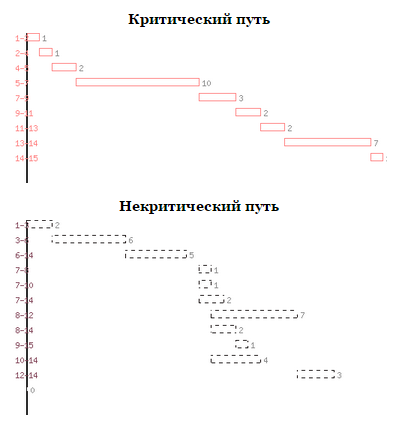
  
•