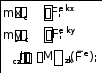Задача д дифференциальные уравнения

• Название: Задача д дифференциальные уравнения
• Дата: 20.03.2022
• Размер: 304.15 Kb.
• Имя файла: dinamika_4.docx
• Тип: Задача; #404929
• страница: 3 из 5

dt

 _M



_z(F^e) ;

где

K_z I_z

• 
  кинетический момент тела () относительно не-
  

подвижной оси Oz;

k
_M_z(F^e)

• 
  сумма моментов всех внешних сил, действую-
  

щих на тело, относительно той же оси.

Если  ^ , то 

 ^

 ^,

dK_z

dt

 I_z^. С учетом этих соотно-

шений получаем дифференциальное уравнение при вращении те- ла вокруг неподвижной оси:

В уравнении (6) величина

I_z=const.

. (6)

3. Плоскоедвижениетвердоготела

При плоском движении фигура () перемещается поступательно вместе с центром масс (точка C) и вращается вокруг центра масс (рис. 136).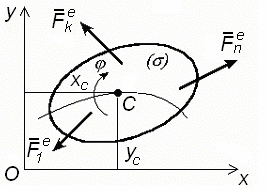



Рис. 136

Запишем уравнения плоского движения:
x_c = x_c(t); y_c = y_c(t); z_c = z_c(t).
Действующие силы _F^e,F^e,F^e_ вызывают плоское движение фи-

гуры ().

1 2 n

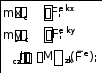Так как плоское движение состоит из поступательного и враща- тельного движений, то нужно записать три дифференциальных уравнения:


(7)

где m–масса фигуры ();

I_cz– момент инерции фигуры относительно оси Cz, перпендику- лярной плоскости чертежа.

Примеррешениязадачи

На рис. 137 представлена механическая система, состоящая из четырех твердых тел, соединенных между собой при помощи не- растяжимых нитей. Заданы следующие величины: m₁ = 8 кг; m₂ = 10кг; m₃ = 4 кг; m₄ = 6 кг – массы тел; F = 80 Н – сила, приложенная к телу 1; f₁ = 0,2 – коэффициент трения скольжения между телом 1 и поверхностью; =30^о - угол наклона поверхности к горизонту;

 = 20^о – угол наклона силы F к траектории движения тела 1; M = 2Нм – момент пары, приложенной к шкиву 2; r₂ = 1/2R₂; R₂ = 0,8 м – малый и большой радиусы шкива 2; ₂= 0,6 м – радиус инерции это- го шкива; R₃=0,4м; R₄=0,6м– радиусы колеса 3и цилиндра 4;

g = 9,8 м/с². Цилиндр 4 катится по плоскости без скольжения. Определить ускорение тела 1 (a₁).

Решение

Обозначим цифрами все нити в системе и найдем кинематиче- ские соотношения между всеми телами системы, выразив их через ускорение тела 1– a₁.

_{ } a^ R R _

a₁ a₁ ,

3_2 _,

^a1 ^r2

a₃ ² a₁  2a₁,

r₂

a₃  a₃;

угловое ускорение шкива ^

₂  <sub>2

</sub> a₁

r<sub>2

</sub> a₁