Задача д дифференциальные уравнения

• Название: Задача д дифференциальные уравнения
• Дата: 20.03.2022
• Размер: 304.15 Kb.
• Имя файла: dinamika_4.docx
• Тип: Задача; #404929
• страница: 5 из 5

 19  78,4 sin30^o

 T₅ , или

8a₁  95,4  T₅ , где

Двухступенчатый шкив 2 вращается (рис. 139) вокруг горизон- тальной оси.

На тело 2действуют следующие силы: P₂=m₂g=109,8=98Н

– сила тяжести тела; T₅=T₅',T₆,T₇–силы натяжения нитей; M –

пара сил.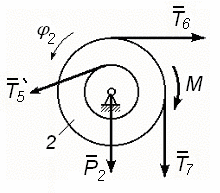



Рис. 139

k
Для тела 2применяем дифференциальное уравнение (6):

^I2z^2

 _M_z(F^e);

где I_2z m

 ²  10  0,6²

 3,6кгм² ; ^  

 2,5a.

Тогда

2 2


5 2 6 7 2
3,6  2,5  a₁  T^'  r
 (T T)  R

2 2 1

,

5 6 7
9a₁  T^'  0,4  0,8 T

 0,8 T.

Окончательно получаем

22,5a₁  T^'  2T 2T.

Тело3

5 6 7

Диск 3(рис. 140) находится в плоском движении.

На диск 3действуют следующие силы: P₃=m₃g=49,8=39,2Н

– сила тяжести диска; T₇, T₈– силы натяжения нитей.

Рис. 140

 _F

;
Запишем дифференциальные уравнения (7) для диска:

_{m3 x}₃

ekx₃

^I3z^3

 _M_z(F^e);

k
третье уравнение – тождество 0  0 , так как

y₃  const и

_F
eky₃

 0 .

При

_x₃

 a₃

 2a₁ и ^₃

 ₃

 5a₁ получим:


_2m₃  a₁  T₇  P₃  T₈;

^{ 1} mR²  

 T R.

^ 2

3 3 3 8 3

Из второго уравнения находим T₈:

mR²  

_{T8 } 3 3 3
_4  0,4  5a₁
 4a₁.

2 2

Из первого уравнения определим T₇:
T₇  2m₃a₁  P₃  T₈  2  4a₁  39,2  4a₁,


или T₇  39,2  12a₁ .

Тело4

Цилиндр 4(рис. 141) находится в плоском движении. Он катится по горизонтальной плоскости без скольжения.



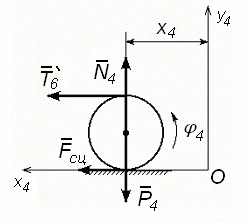
Рис. 141
На цилиндр действуют силы: P₄ = m₄g = 69,8 = 58,8 Н – сила тяже- сти цилиндра; N₄ – реакция нормального давления; F_сц – сила тре- ния сцепления; T₆^’– сила натяжения нити (T₆= T₆^’).

Для цилиндра запишем дифференциальные уравнения (7):


kx₄
m₄^x^₄ = _F^e ;

ky₄
m₄^y^₄ = _F^e ;

k
I_4z^4 = _M_z(F^e ) .

При

_x₄

 a₄

 a₁,

_₄

 ₄

 1,67a₁,

y₄  R₄

 const,

I  ¹ mR²  ¹  6  0,6²
 1,08
(кгм²)

4z ₂ 4 4 ₂

система уравнений принимает вид:


6
6a₁  T^'  F_сц;

0  N₄  P₄ ;

1,08 1,67  a₁  T^'  R F
 R.

Откуда

N₄  P₄
 58,8 Н;

6 4 сц4


_^{6a1  T6  Fсц;}

3a T^  F .

_⎩^ 1 6 сц
В полученных уравнениях исключаем силу F_сци получим


T₆^  4,5a₁ .

Составим систему алгебраических уравнений, полученных для каждого тела:

<sup>8a1  95,4  T5 ;

</sup>22,5a T^  2T 2T;

^ 1 5 6 7



где

T₅  T₅^ ; T<sub>6

</sub>12a₁  39,2  T₇ ;

^_4,5a₁  T₆^ ;

 T₆^ .

Из последних уравнений находим

T₆^  T₇  39,2  16,5a₁.

Первое и второе уравнения сложим

T₆  T₇  15,2a₁  47,7 .

Получаем конечное уравнение

31,7a₁  8,5  0 , откуда

a₁ 

8,5

31,7

 0,27
м/с².