Главная страница
Навигация по странице:

  • Дифференциальные уравнения движения механиче

    		•

    Задача д дифференциальные уравнения


    Скачать 304.15 Kb.
    НазваниеЗадача д дифференциальные уравнения
    Дата20.03.2022
    Размер304.15 Kb.
    Формат файлаdocx
    Имя файлаdinamika_4.docx
    ТипЗадача
    #404929
    страница1 из 5
      1   2   3   4   5







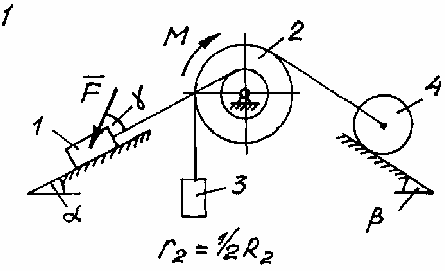
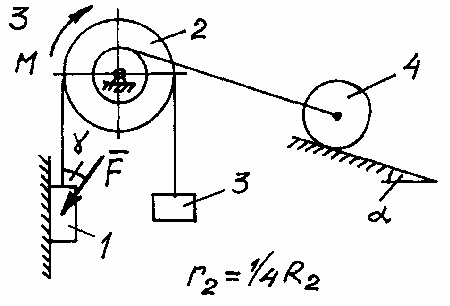
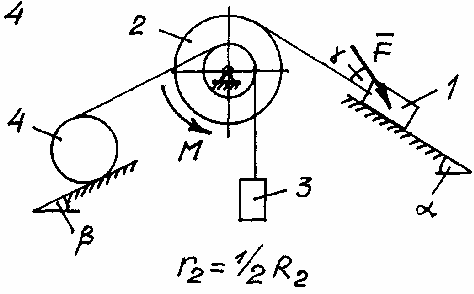
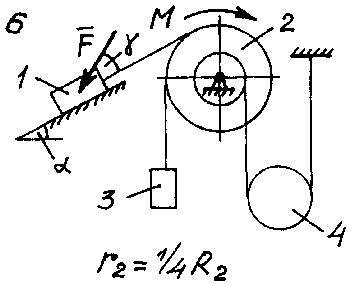
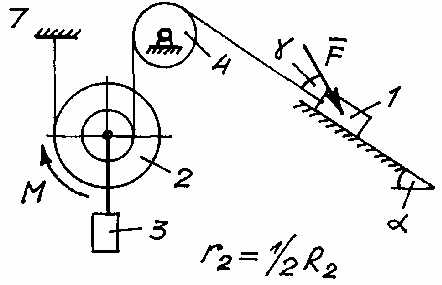
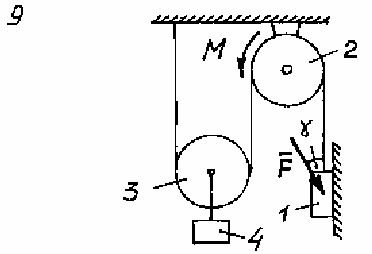
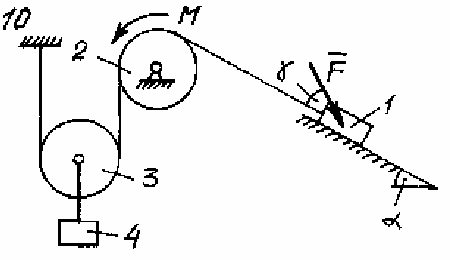
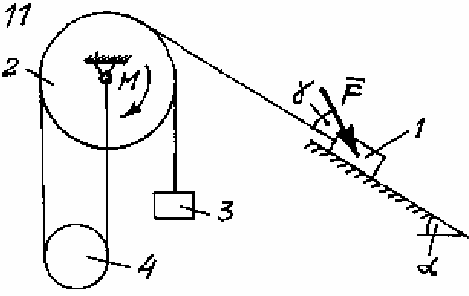
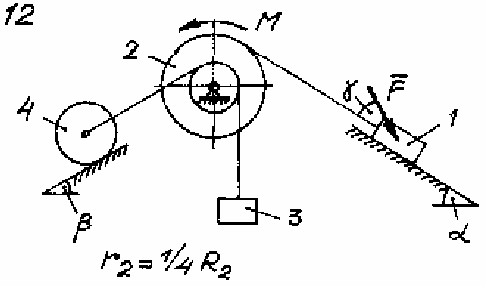
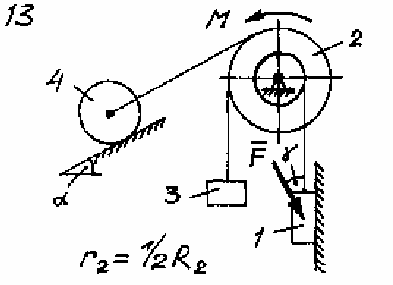
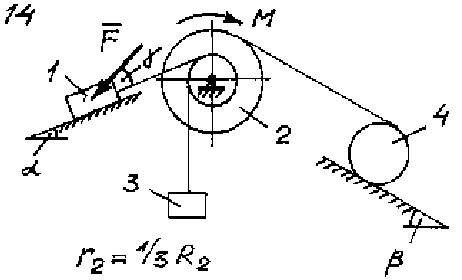
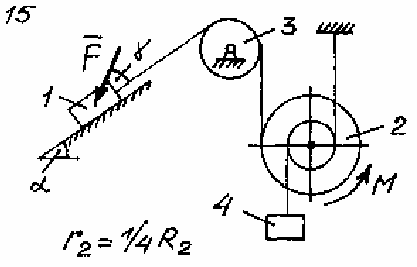
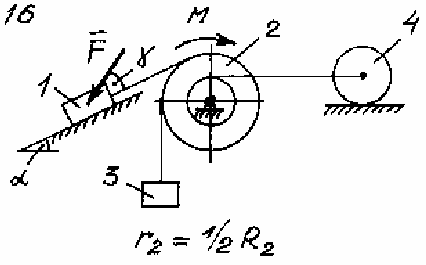
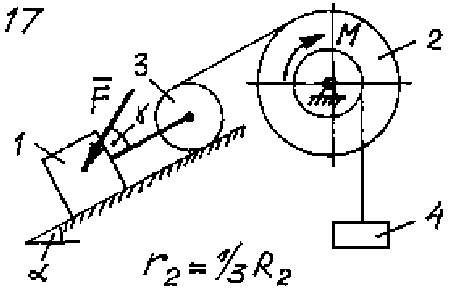
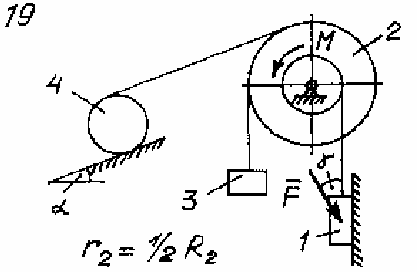
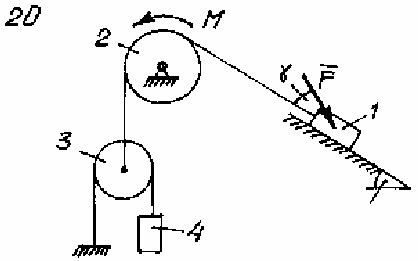
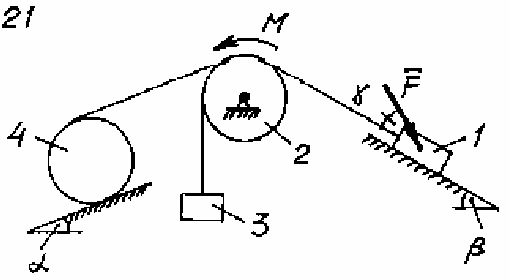
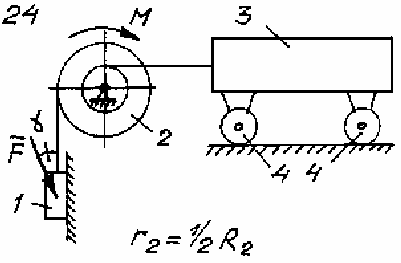
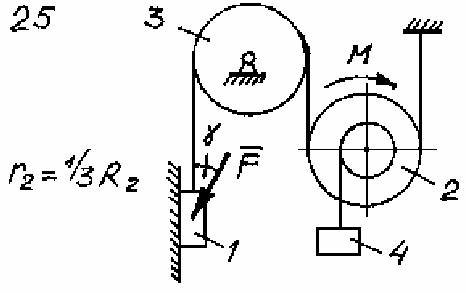
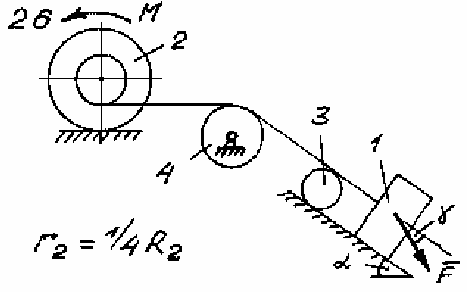
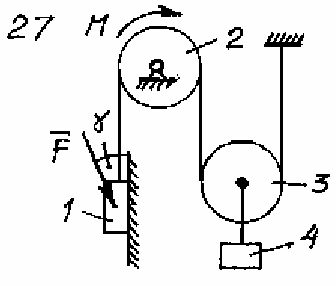
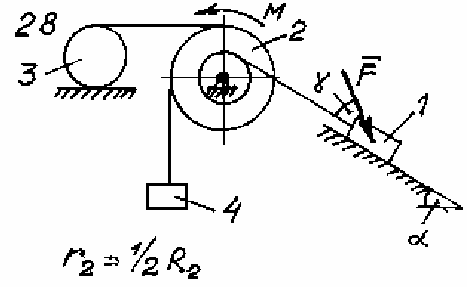
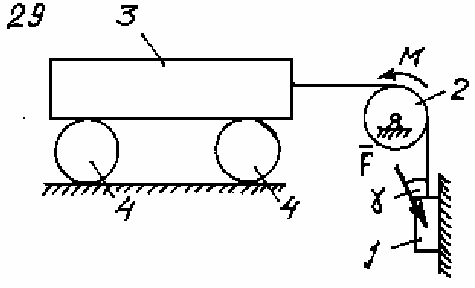
    Задача Д.4.Дифференциальные уравнениядвижениятвердоготела

    Механическая система (рис. 132 – 134) состоит из четырех твердых тел, соединенных между собой при помощи нерастяжимых нитей. Заданы следующие параметры: m1, m2, m3, m4– массы тел; r2,R2–малый и большой радиусы двухступенчатого шкива 2; F-

    сила, действующая на тело 1, которое скользит по шероховатой

    поверхности; f1= 0,3 – коэффициент трения скольжения для всех вариантов; 2=0,4м– радиус инерции шкива 2для всех вариантов; M – момент, приложенный к телу 2. Для определения сил тяжестей тел ис- пользовать ускорение свободного падения g=9,8м/с2.

    Используя дифференциальные уравнения движения твердых тел, определить ускорение тела 1(a1).

    Необходимые для расчета числовые величины приведены в таблице 13.

    Дифференциальные уравнения движения механиче-скойсистемы

    Механическая система состоит из совокупности материальных

    точек A1; A2;; An, где m1;m2;;mn

    - масса этих точек. На


    k
    k
    каждую Akточку (рис. 135) действуют силы: внутренняя сила.



    Fe- внешняя сила;


    F i -


    Радиус-вектор центра масс (точка C) системы

    по формуле (1)

    rcопределяется

    r mkrk c m

    n
    , (1)

    где

    m mk- масса механической системы;

    k1



















    Рис. 132




















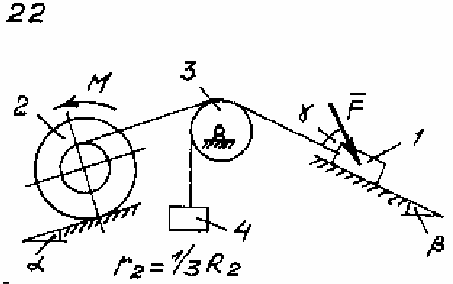
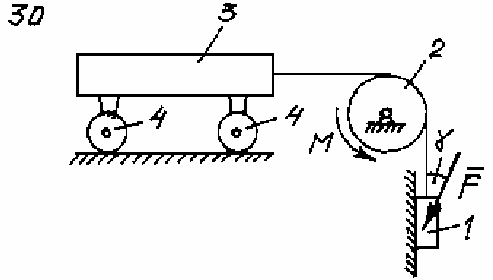
    Рис. 133



















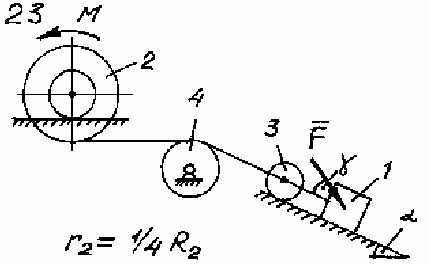
    Рис. 134

    Таблица 13


    Номер варианта (рис. 132

    - 134)
    m1
    m2
    m3
    m4
    F
    M
    R2
    R3
    R4









    кг
    кг
    кг
    кг
    Н
    Нм
    м
    м
    м
    град
    град
    град

    1
    10
    6
    4
    8
    80
    2
    0,8
    -
    0,4
    30
    45
    40

    2
    8
    6
    4
    2
    60
    3
    0,9
    0,5
    -
    45
    -
    30

    3
    6
    8
    6
    4
    70
    2
    0,8
    -
    0,6
    30
    -
    45

    4
    4
    8
    6
    8
    60
    3
    1,2
    -
    0,5
    30
    30
    30

    5
    6
    8
    6
    4
    40
    2
    0,9
    -
    0,4
    -
    -
    45

    6
    4
    6
    4
    6
    50
    3
    1,2
    -
    0,3
    -
    -
    30

    7
    5
    8
    4
    4
    60
    2
    0,8
    -
    0,4
    60
    -
    20

    8
    8
    6
    5
    4
    80
    3
    0,9
    0,6
    -
    30
    60
    20

    9
    6
    8
    4
    4
    40
    2
    0,6
    0,8
    -
    -
    -
    30

    10
    4
    6
    8
    4
    60
    3
    0,5
    0,6
    -
    30
    -
    45

    11
    6
    8
    4
    4
    80
    2
    0,8
    -
    -
    45
    -
    30

    12
    8
    10
    4
    6
    60
    3
    1,2
    -
    0,6
    30
    30
    20

    13
    6
    8
    4
    5
    40
    2
    0,8
    -
    0,5
    30
    -
    45

    14
    4
    8
    4
    6
    60
    3
    0,9
    -
    0,4
    45
    60
    30

    15
    8
    8
    4
    6
    80
    2
    1,2
    0,6
    -
    30
    -
    20

    16
    10
    8
    4
    5
    60
    3
    1,0
    -
    0,6
    30
    -
    30

    17
    8
    10
    6
    4
    80
    2
    0,9
    0,5
    -
    45
    -



    18
    6
    8
    4
    6
    40
    3
    1,2
    -
    0,4
    30
    -
    30

    19
    8
    10
    4
    8
    60
    2
    0,8
    -
    0,5
    30
    -
    20

    20
    6
    8
    6
    4
    80
    2
    0,6
    0,8
    -
    30
    -
    45

    21
    10
    6
    4
    6
    80
    3
    0,8
    -
    0,6
    30
    45
    30

    22
    8
    10
    6
    4
    60
    2
    0,9
    0,6
    -
    45
    60
    30

    23
    6
    8
    4
    6
    60
    3
    1,2
    0,4
    0,6
    45
    -
    20

    24
    8
    10
    6
    4
    80
    2
    0,8
    -
    0,4
    -
    -
    30

    25
    6
    8
    6
    4
    80
    3
    0,9
    0,5
    -
    -
    -
    20

    26
    8
    10
    4
    6
    70
    2
    1,2
    0,4
    0,6
    30
    -
    20

    27
    8
    6
    8
    4
    80
    3
    0,6
    0,8
    -
    -
    -
    30

    28
    10
    8
    6
    4
    60
    2
    1,2
    0,8
    -
    45
    -
    20

    29
    6
    4
    8
    4
    40
    3
    0,8
    -
    0,4
    -
    -
    30

    30
    8
    6
    10
    4
    60
    2
    0,8
    -
    0,4
    -
    -
    20

    rk- радиус-вектор k–ой точки.




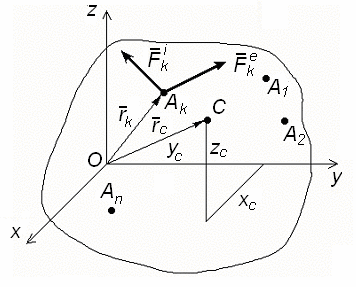    Рис. 135

    Для Akточки запишем основное уравнение динамики:




    mkak Fe Fi



    (k 1,n); (2)

    где ak

    k k

    - вектор ускорения точки.

    Но ak

    d2rk

    dt2

    , поэтому mk

    d2rk



    dt2

    d2



    dt2 (mkrk) .

    Для системы материальных точек будем иметь n– уравнений (2).

    Суммируем эти уравнения

    n n n

    mkak

    Fe

    • Fi

    . (3)


    k1 k1

    d2 d2

    k k

    k1

    Но mkak 2 (mkrk)
      1   2   3   4   5

    написать администратору сайта