контрольная работа. Задача Даны векторы а 2 12 0, b
 Скачать 158.5 Kb. Скачать 158.5 Kb.
|
|
Задача 1. Даны векторы а = {2; 12; 0}, b = {4.75; -4; 3.75}, c = {6; 6; 2}, и d = {12,75; 15; 5,75} в декартовой системе координат. Показать, что векторы а, b, c, образуют базис Найти координаты вектора d в этом базисе. Решение. Так как каждый вектор задан тремя координатами, то в рассматриваемом векторном пространстве существует базис 1а + 2b + 3с = которое можно записать для соответствующих координат этих векторов 2  1 + 4,752 + 63 = 0, 1 + 4,752 + 63 = 0,121 - 42 + 63 = 0, 3,752 + 23 = 0. Решим полученную систему линейных уравнений методом Гаусса. 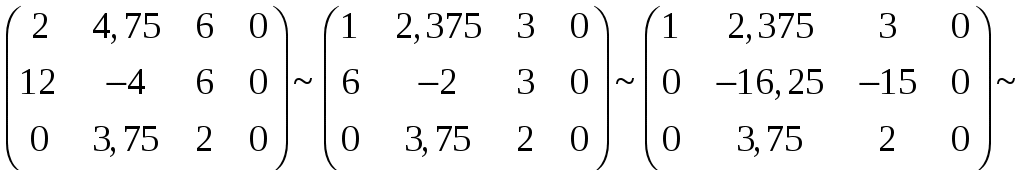 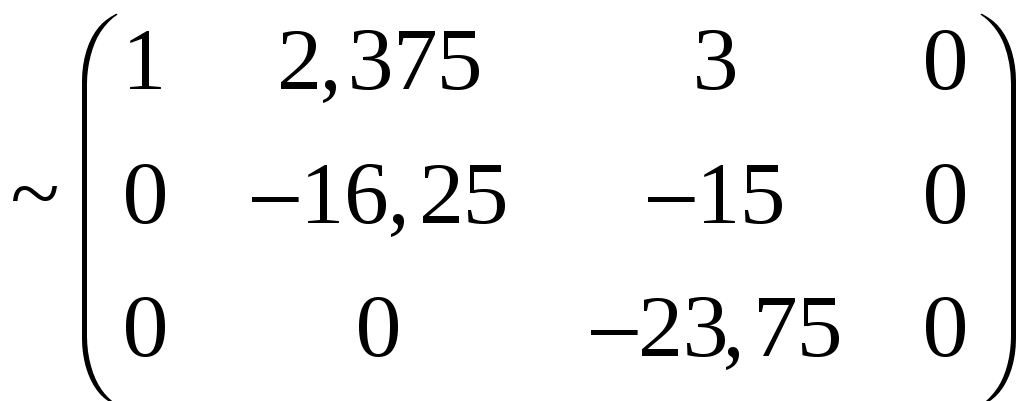 . .Отсюда получаем единственное нулевое решение 1 = 2 = 3 = 0, то есть векторы а, b, c являются линейно независимыми и, следовательно, образуют базис пространства. Найдем теперь разложение вектора d по базису а, b, c из условия выполнения векторного равенства d = 1а + 2b + 3c, которое для соответствующих координат запишется 2  1 + 4,752 + 63 = 12,75, 1 + 4,752 + 63 = 12,75,121 - 42 + 63 = 15, 3,752 + 23 = 5,75. Полученную квадратную систему линейных уравнений относительно неизвестных 1, 2, 3 решим по формулам Крамера. Вычислим определители 3–го порядка: 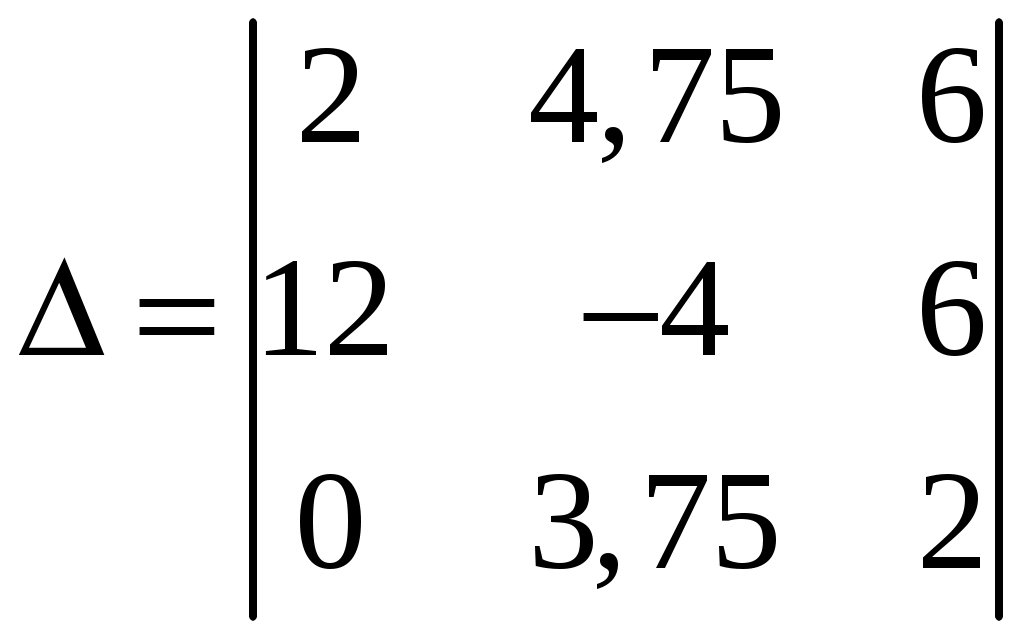 = 95, = 95,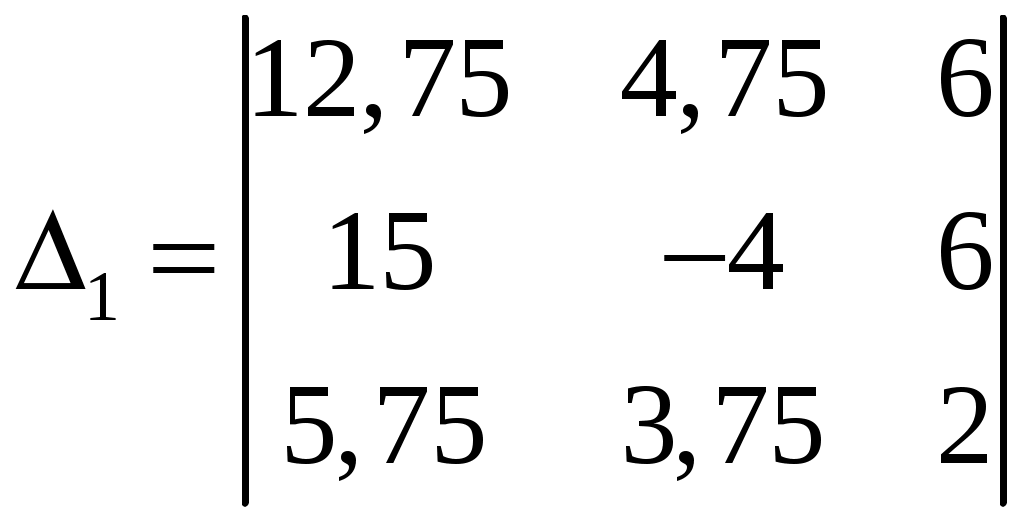 = 108, = 108,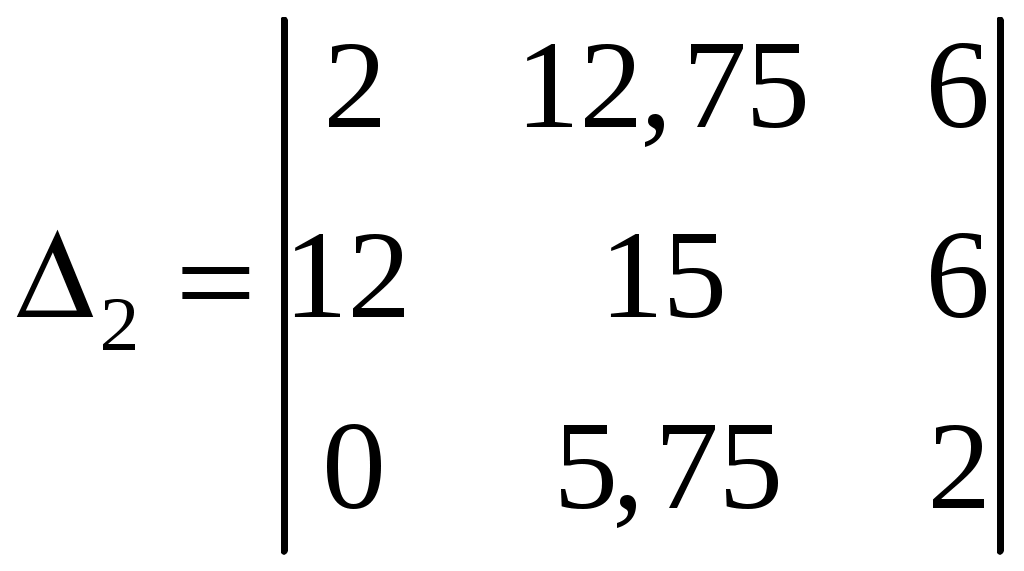 = 99, = 99,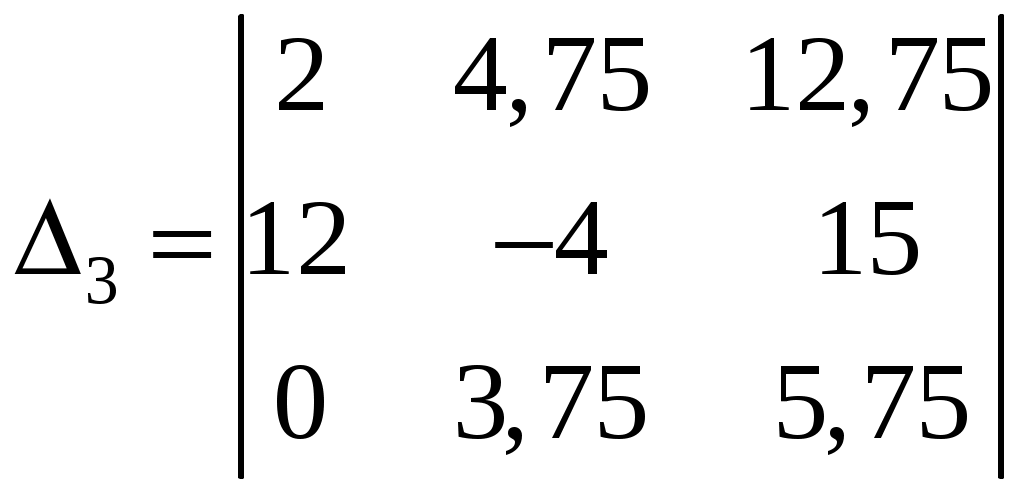 = 87,5. = 87,5.Тогда по формулам Крамера находим координаты вектора d в базисе а, b, c: В итоге имеем d = Задача 50. Найти указанные пределы, не пользуясь правилом Лопиталя. а) 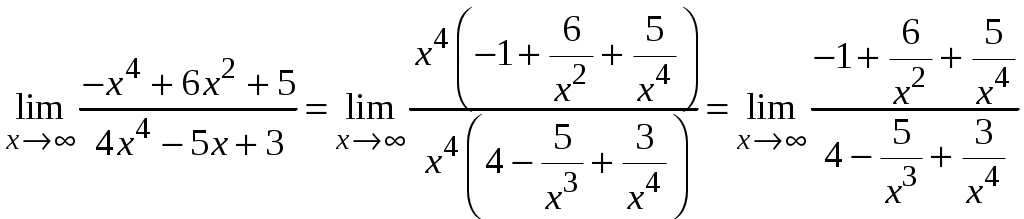 = =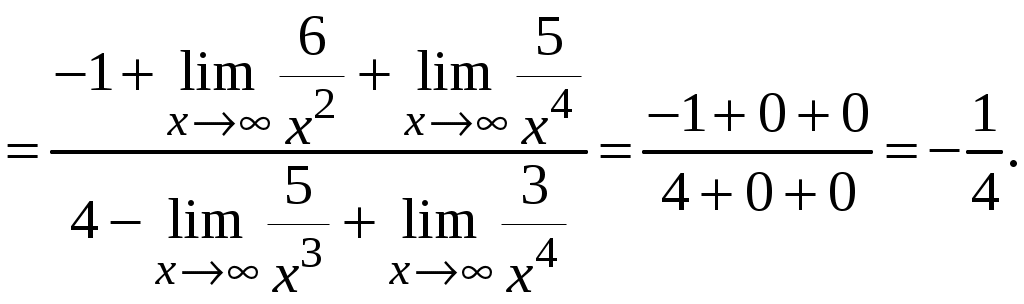 б) 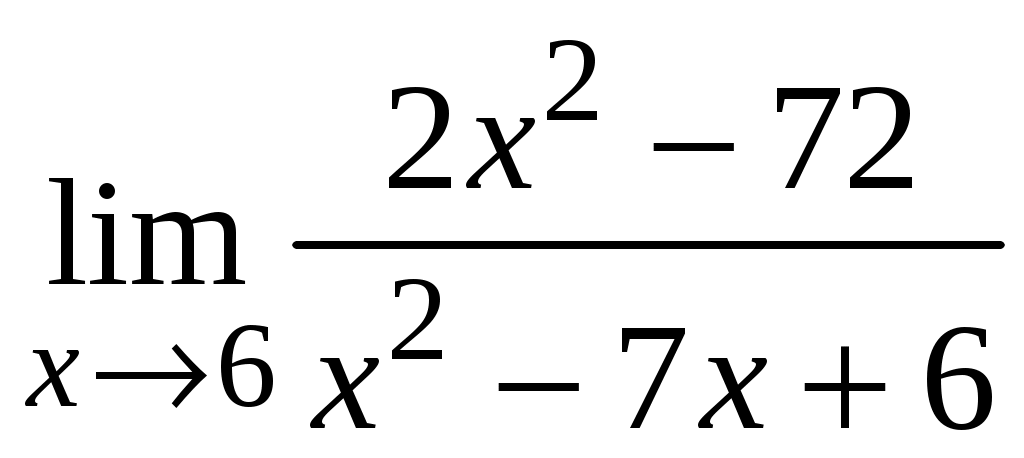 . Непосредственной подстановкой убеждаемся, что существует неопределенность . Непосредственной подстановкой убеждаемся, что существует неопределенность Отсюда 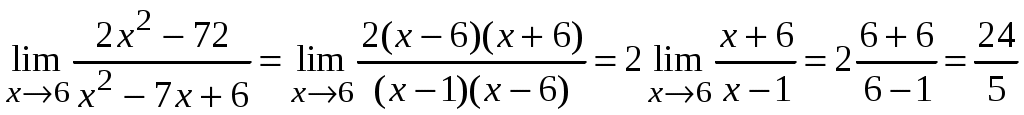 . .в) 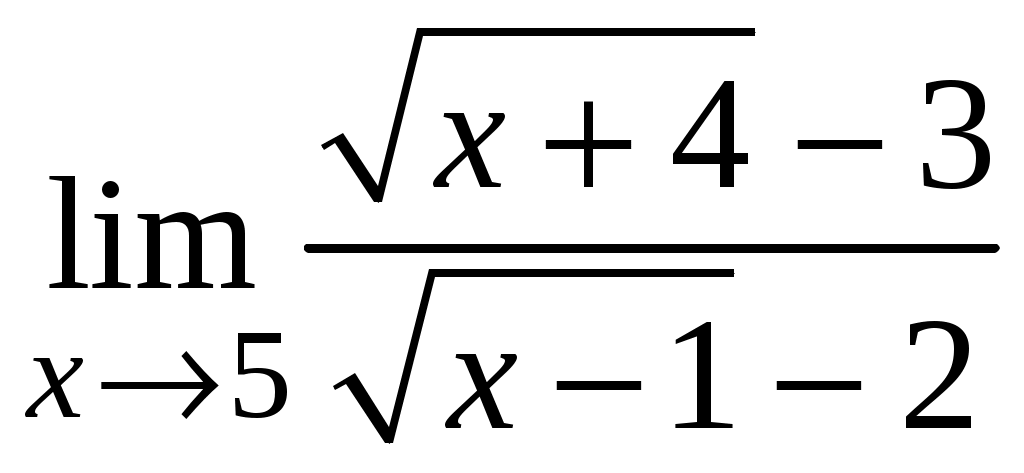 . Непосредственной подстановкой убеждаемся, что существует неопределенность . Непосредственной подстановкой убеждаемся, что существует неопределенность 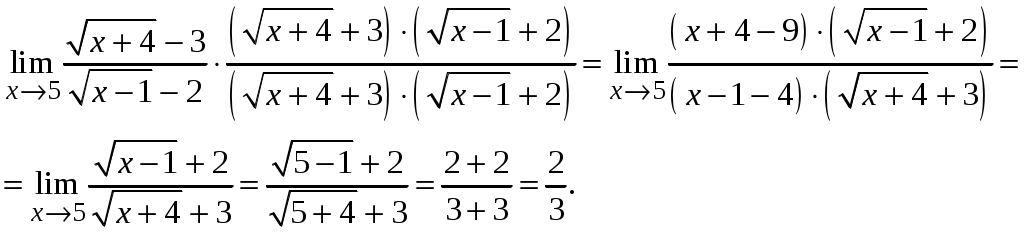 г) 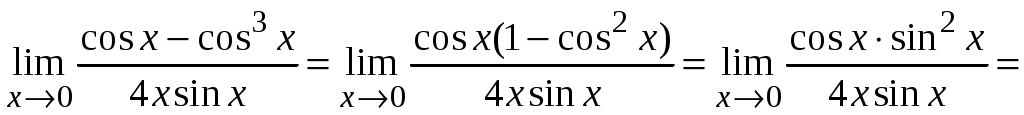 д) 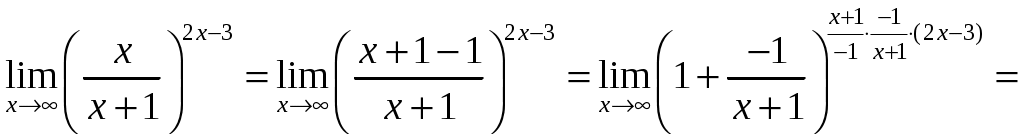 Задача 80. Найти производные а) 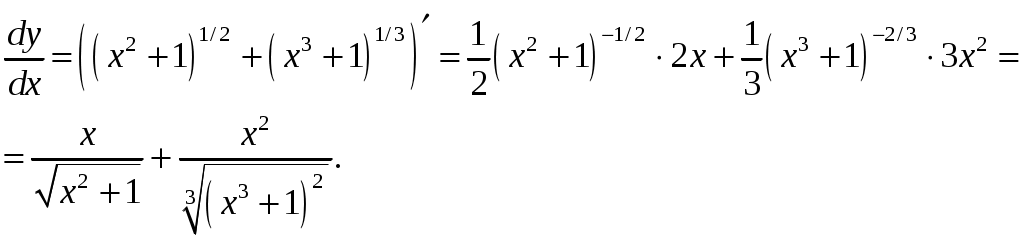 б) 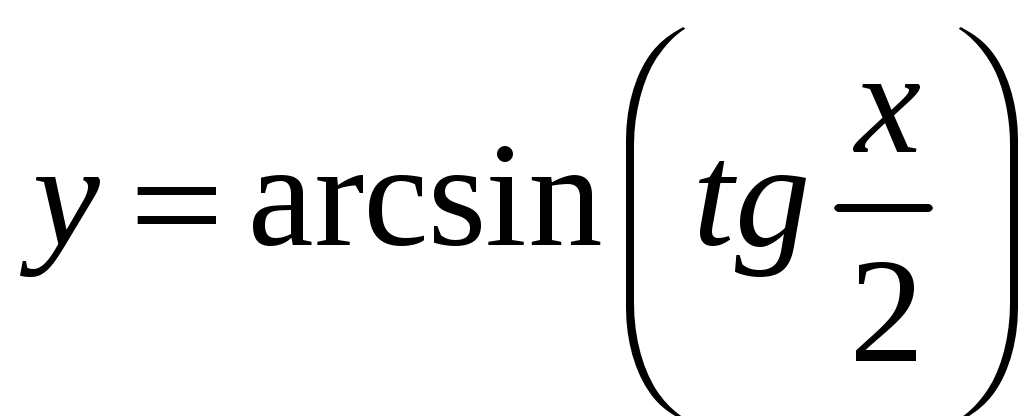 . .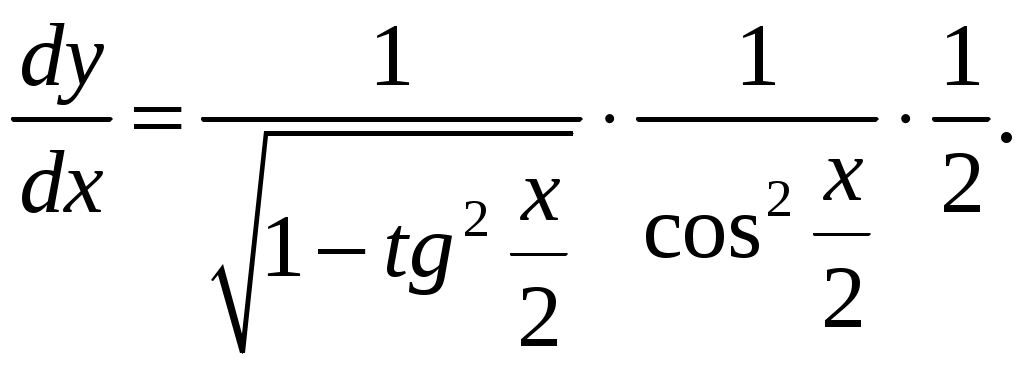 в) 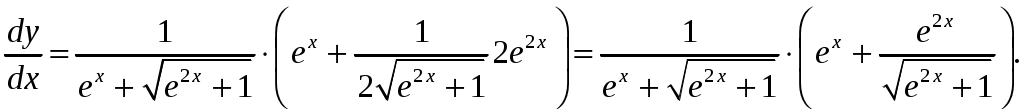 г) 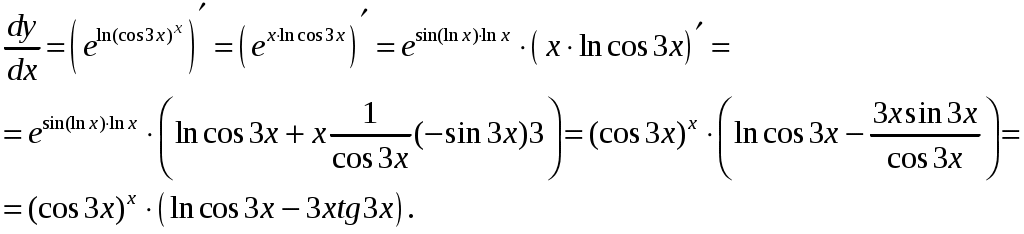 Задача 90. Для данных функций найти Решение. а) 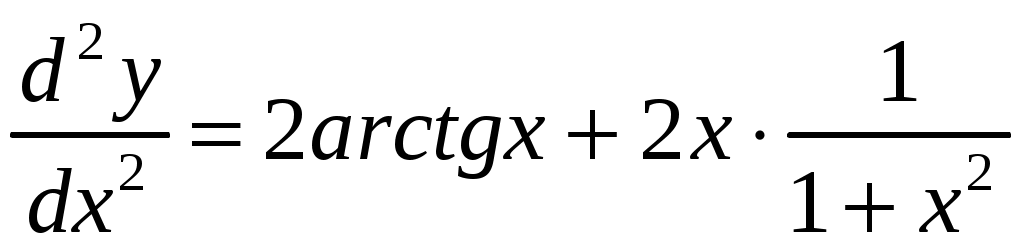 . .б) 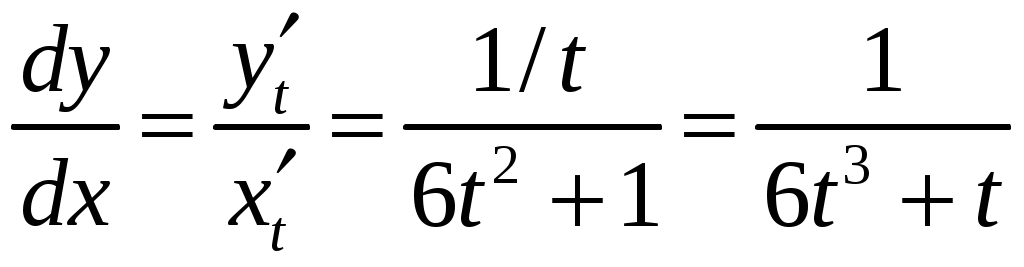 ; ;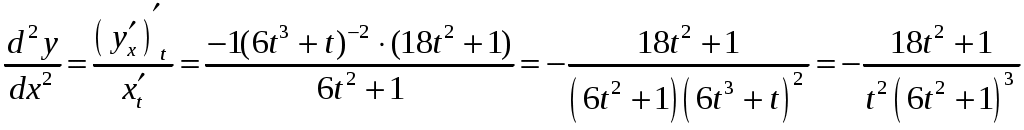 . .Задача 110. Пользуясь правилом Лопиталя, вычислить пределы: а) 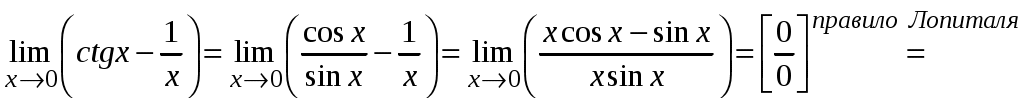 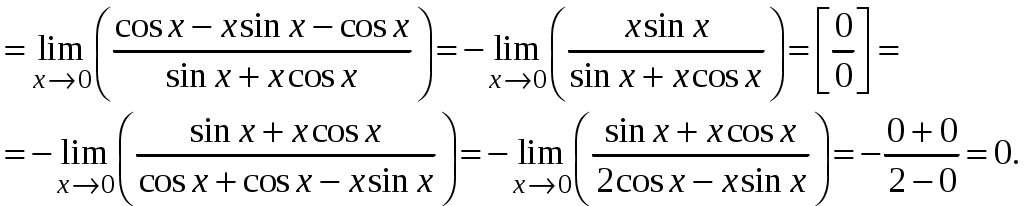 б) 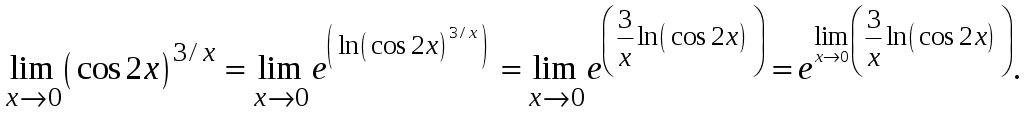 Рассмотрим 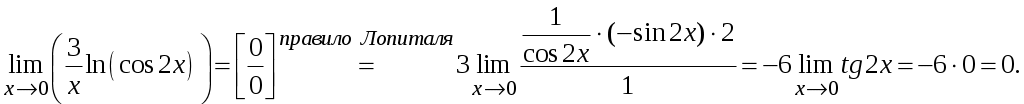 Отсюда |
