Экз. билет №17. Задача Для функции y x cos(2X) (X 1,50,1) оценить точность контроля, если ошибка измерительной системы 2%, а частота контроля через каждые 4 значения.

• Название: Задача Для функции y x cos(2X) (X 1,50,1) оценить точность контроля, если ошибка измерительной системы 2%, а частота контроля через каждые 4 значения.
• Дата: 07.03.2022
• Размер: 149.23 Kb.
• Имя файла: Экз. билет №17.docx
• Тип: Задача; #385765

Экзаменационный билет №17

1. 
   
   Какие параметры используются для оценки точности измерений?
   
2. 
   Для переменной, описываемой функцией Y = cos(X); X = [1,50,1]. Какой метод контроля точнее:
   

c. Ошибка контроля 10%, а частота контроля – каждое значение Y.

d. Ошибка контроля 1%, а частота контроля – каждое 10-е значение Y.

3. Задача: Для функции Y = X + cos(2*X) (X = [1,50,1]) оценить точность контроля, если ошибка измерительной системы 2%, а частота контроля через каждые 4 значения. По результатам рассчитать ошибку контроля и построить графики фактического изменения Y и результатов измерений. Результат представить в виде файла WORD, а расчёты в файле EXCEL.

Ответ на 1 вопрос.

Оценка точности измерений

Оценить точность измерений – это определить сравнимые числовые характеристики, которые выражают качественную сторону самих измерений и условий их проведения. Числовые характеристики измерений устанавливаются с помощью теории ошибок и всем известной теории вероятности. Согласно теориям ошибок и вероятности оценка точности измерений обязательно производится по случайным ошибкам.

Параметрами для определения оценки точности измерений служат:

1. 
   Средняя квадратическая ошибка измерений;
   
2. 
   Относительная ошибка;
   
3. 
   Предельная ошибка.
   

Формула для определения средней квадратической ошибки:

M = 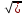((d1^2 + d2^2 + d3^2 + … + dn^2)/n), где d1, d2, d3, …, dn – случайные погрешности измерений,

n – количество случайных погрешностей измерений.

Формула для определения относительной ошибки измерений:

E(a) = (delta(a)/a) * 100%

Относительной погрешностью измерения называется отношение абсолютной погрешности delta(a) к приближённому значению измеряемой величины a.

Такая погрешность измерения показывает, какую часть составляет абсолютная погрешность измерения от приближённого значения измеряемой величины.

Предельная ошибка – это наибольшее значение случайной ошибки, которое может появиться при данных условиях равноточных измерений.

Формула для определения предельной ошибки:

d1 = sqrt(d11^2 + d12^2 + … + d1n^2), где

d11 – основные погрешности средств измерений;

d12 – инструментальная погрешность;

d1n – прочие погрешности.

О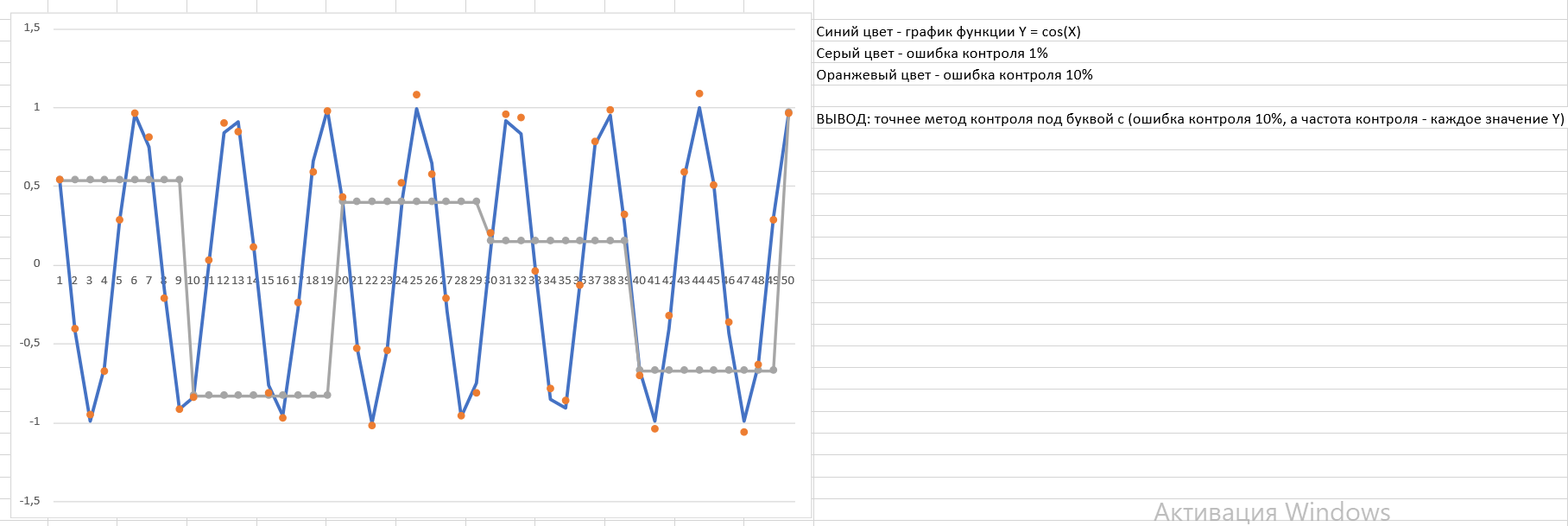
твет на 2 вопрос.

Точнее метод контроля по буквой c (ошибка контроля 10%, а частота контроля – каждое значение Y).

Ответ на 3 вопрос.

1. 
   Сначала ищем значения в точках X от 1 до 50 ( от =A2 + cos(2*A2) до = A51 + cos(2*A51)
   
2. 
   Затем ищем погрешность по формуле, начиная с =B5+(((СЛЧИС()-0,5)*2)*$H$2) и заканчивая B49+(((СЛЧИС()-0,5)*2)*$H$2), учитывая только каждое 4-е значение (B5, B9, B13, B17, B21, B25, B29, B33, B37, B41, B45, B49).
   
3. 
   После этих вычислений мы ищем разность между значением графика и значением погрешности.
   
4. 
   На основе всех вычислений строим график функции y = X + cos(2*X) и погрешности.
   
5.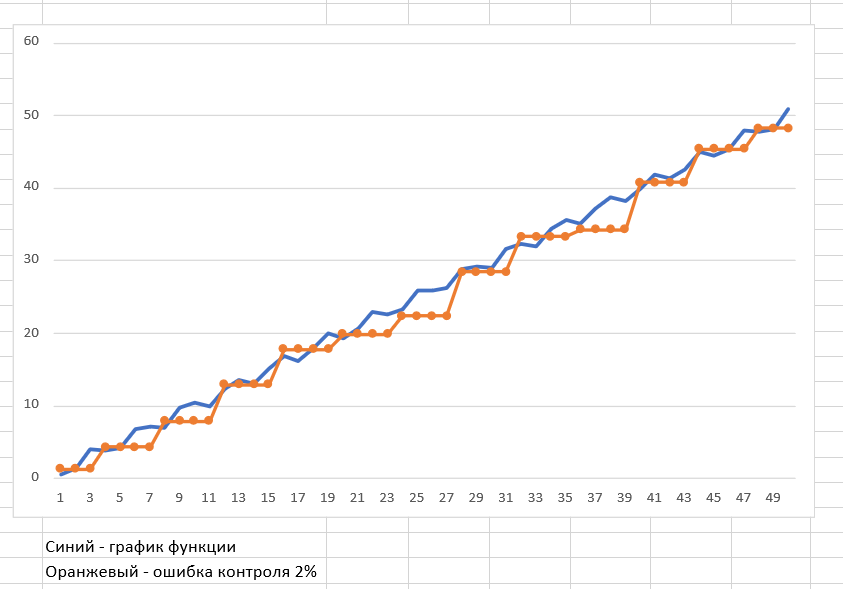 
   Y
   max = 50.86232, Y (2%) = 1.01725.