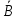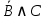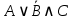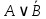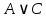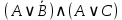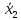Контрольная по ПМ. Задача Доказать логические тождества
 Скачать 80.96 Kb. Скачать 80.96 Kb.
|
|
Контрольная работа (1-й семестр) Задача 1. Доказать логические тождества: 1.5. 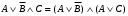 . .Решение: докажем тождество составив таблицы истинности для обеих его частей.
Таблица истинности показывает совпадение значений обеих частей тождества. Задача 2. Представить булеву функцию в виде СДНФ и начертить схему, реализующую эту функцию. 2.5. 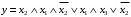 Решение: для представления булевой функции в виде совершенной дизъюнктивной нормальной форме (СДНФ) составим таблицу истинности:
В таблице истинности отметим все наборы переменных, на которых функции значение функции равно 1. Для каждого отмеченного набора запишем конъюнкцию по правилу: если значение переменной есть 1, то в конъюнкцию включаем саму переменную, иначе её отрицание: 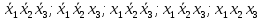 . .Все полученные конъюнкции связываем операциями дизъюнкции: 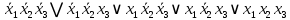 – искомая СДНФ. – искомая СДНФ.Задача 3. Найти интеграл: 3.1 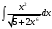 Решение: применим для вычисления интеграла метод замены переменной. Пусть 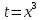 , тогда , тогда 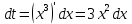 , а , а 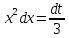 . Подставим найденное под знак интеграла. . Подставим найденное под знак интеграла.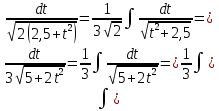 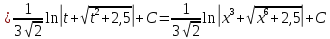 Вычислить или доказать расходимость 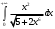 Решение: при вычислении интеграла выполним предельный переход, если полученный предел конечен, то интеграл сходится. 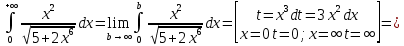 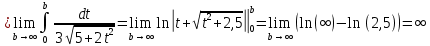 Интеграл равен , следовательно, расходится. 3.2. Найти интеграл: 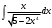 Решение: 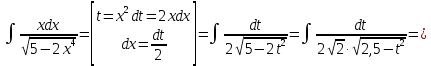 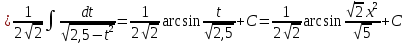 Вычислить или доказать расходимость 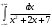 Решение: Выделим в знаменателе полный квадрат 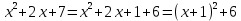 , тогда , тогда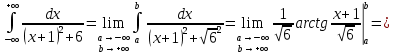 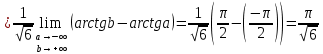 3.3 Найти интеграл 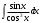 Решение: применим метод замены переменной 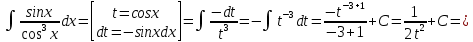 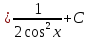 Вычислить или доказать расходимость 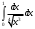 Решение: 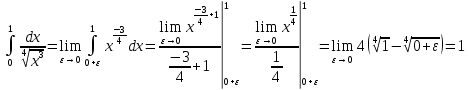 3.4 Найти интеграл 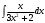 Решение: 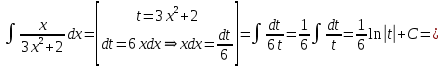 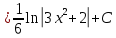 Вычислить или доказать расходимость 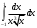 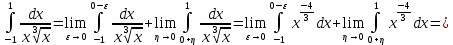 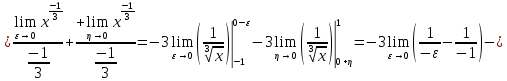 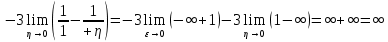 Несобственный интеграл расходится. 3.5 Найти интеграл 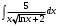 Решение: применим метод замены переменной, пусть 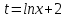 , тогда , тогда 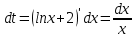 , подставим найденное под знак интеграла , подставим найденное под знак интеграла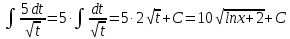 Вычислить или доказать расходимость 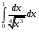 Решение: 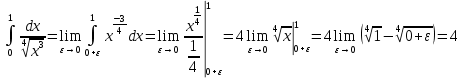 3.6 Найти интеграл 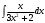 Решение: 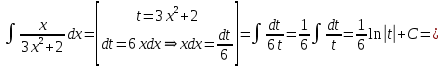 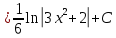 Вычислить или доказать расходимость 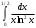 . .Решение: 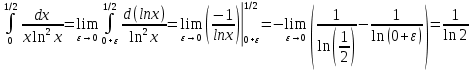 3.7 Найти интеграл 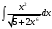 Решение: применим метод замены переменной 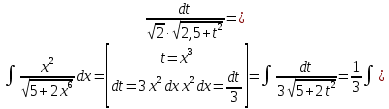 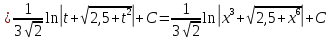 Вычислить или доказать расходимость 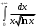 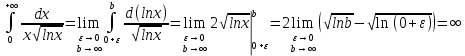 3.8 Найти интеграл 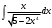 Решение: применим в решении метод замены переменной 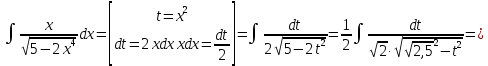 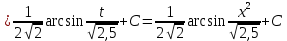 Вычислить или доказать расходимость 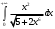 Решение: при вычислении интеграла выполним предельный переход, если полученный предел конечен, то интеграл сходится. 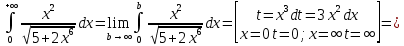 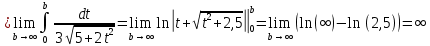 Интеграл равен , следовательно, расходится. 3.9 Найти интеграл 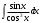 Решение: применим метод замены переменной 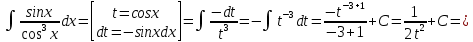 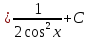 Вычислить или доказать расходимость 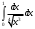 Решение: 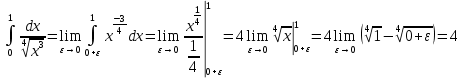 3.10 Найти интеграл 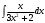 Решение: 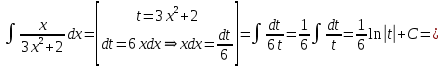 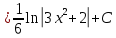 Вычислить или доказать расходимость 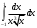 . .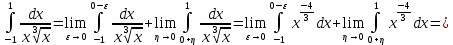 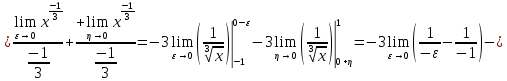 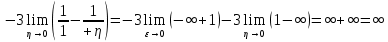 Несобственный интеграл расходится. Задача 4. Исследовать сходимость числового ряда. 4. 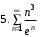 ; ; Решение: Для установления сходимости ряда воспользуемся признаком Даламбера. Общий член ряда равен 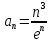 , тогда , тогда 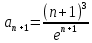 . . Вычислим предел 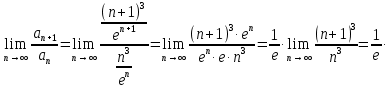 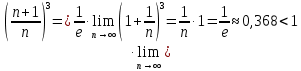 Следовательно, по признаку Даламбера исходный ряд сходится. Задача 5. Найти область сходимости степенного ряда. 5.5. 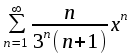 Решение: Общий член данного числового ряда имеет вид: 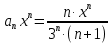 , тогда , тогда 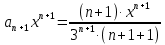 . .Вычислим предел отношения 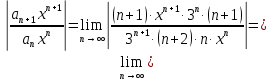 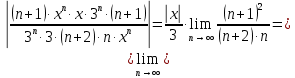 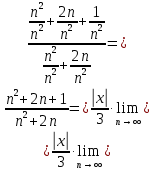 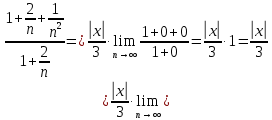 Исходный ряд будет сходиться по признаку Даламбера при условии, что полученное значение предела меньше 1. 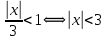 . Опустив знак модуля, получаем двойное неравенство, определяющее искомый интервал . Опустив знак модуля, получаем двойное неравенство, определяющее искомый интервал 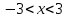 . Исследуем сходимость ряда на границах интервала. . Исследуем сходимость ряда на границах интервала.При 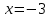 , имеем ряд , имеем ряд 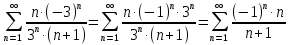 Исследуем его на сходимость по признаку Лейбница: ряд сходится, если является знакочередующимся и его члены убывают по абсолютной величине. 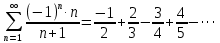 Ряд является знакочередующимся. Вычислим предел 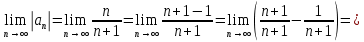 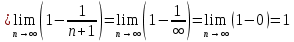 Т.к. предел отличен от 0, ряд расходится. При 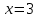 , получаем ряд , получаем ряд 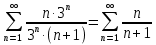 Предел общего члена ряда 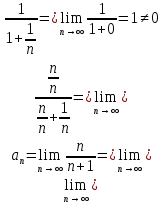 Ряд расходится, т.к. не выполняется необходимый признак сходимости ряда. Т.о. область сходимости ряда интервал (-3; 3). Задача 6. Вычислить определенный интеграл с точностью до 0,001, разложив подынтегральную функцию в ряд, и, затем, проинтегрировав ее почленно. 6.5. 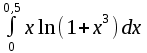 . . Решение: Воспользуемся известным разложением элементарной функции 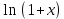 в ряд: в ряд: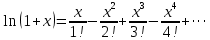 , тогда , тогда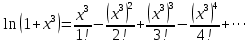 , а , а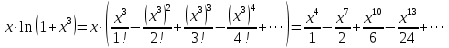 Проинтегрируем полученное выражение 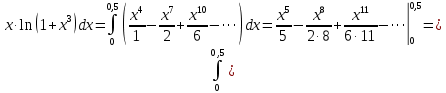 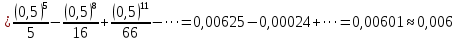 . . |