ТФКП, ряды. ИПР31 и ИПР32_вариант 27. Задача Исследуйте сходимость числового ряда, применив для этого подходящий признак сходимости. Решение
 Скачать 0.63 Mb. Скачать 0.63 Mb.
|
|
Индивидуальная практическая работа ИПР3-1 Вариант 27 Задача 1. Исследуйте сходимость числового ряда, применив для этого подходящий признак сходимости. 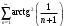 Решение:Воспользуемся необходимым признаком сходимости. Для этого вычислим предел: 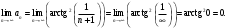 Поскольку 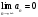 , данный ряд сходится. , данный ряд сходится.Задача 2. Исследуйте сходимость числового ряда, применив для этого подходящий признак сходимости. 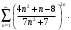 Решение:Используем радикальный признак Коши. 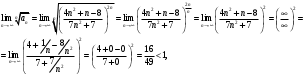 значит данный ряд сходится. Задача 3. Исследуйте сходимость числового ряда, применив для этого подходящий признак сходимости. 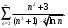 Решение:Используем признак Даламбера. Сравним данный ряд со сходящимся гармоническим рядом 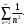 Используем признак сравнения: Если 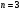 , то , то 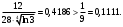 Если 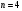 , то , то 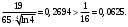 Если 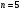 , то , то 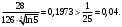 Если 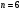 , то , то 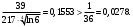 Таким образом, для всех членов ряда выполнено неравенство 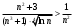 , значит, по признаку сравнения исследуемый ряд сходится вместе с гармоническим рядом , значит, по признаку сравнения исследуемый ряд сходится вместе с гармоническим рядом 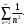 Задача 4. Исследуйте сходимость знакочередующегося ряда. Установите характер сходимости (абсолютная или условная). 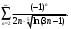 Решение: Рассмотрим ряд, составленный из модулей членов данного ряда 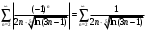 и исследуем его сходимость. и исследуем его сходимость.Так как 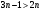 , n 2, то , n 2, то 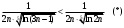 Исследуем сходимость мажорирующего ряда 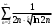 интегральным признаком. интегральным признаком.Положим 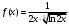 для для 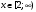 . Убедимся в том, что условия интегрального признака сходимости выполняются для функции . Убедимся в том, что условия интегрального признака сходимости выполняются для функции 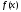 на промежутке [2; +). Исследуем монотонность функции на промежутке [2; +). Исследуем монотонность функции 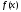 с помощью производной: с помощью производной: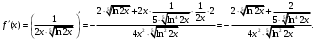 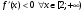 , следовательно, функция , следовательно, функция 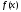 монотонно убывает на промежутке [2; +). Кроме того монотонно убывает на промежутке [2; +). Кроме того 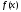 непрерывна и неотрицательна на этом промежутке. непрерывна и неотрицательна на этом промежутке.Таким образом, условия интегрального признака для функции 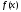 на промежутке [2; ) выполнены. на промежутке [2; ) выполнены.Исследуем теперь сходимость несобственного интеграла 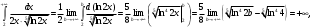 Несобственный интеграл расходится, следовательно, по интегральному признаку Коши ряд 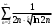 тоже расходится. В таком случае из неравенства (*) по признаку сравнения вытекает расходимость мажорируемого ряда тоже расходится. В таком случае из неравенства (*) по признаку сравнения вытекает расходимость мажорируемого ряда 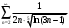 . . Таким образом, окончательно получаем: исходный ряд 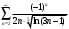 сходится условно. сходится условно.Задача 5. Найдите интервал и область сходимости степенного ряда. 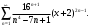 Решение: 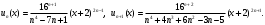 С помощью признака Даламбера найдем интервал сходимости данного ряда: 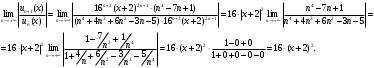 Итак, ряд сходится при 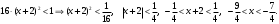 Получили, что интервал сходимости: 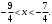 а) Исследуем сходимость ряда в точке 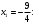 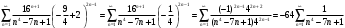 Сравним данный ряд со сходящимся рядом 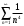 . Используем предельный признак сравнения: . Используем предельный признак сравнения: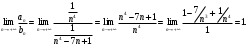 Получено конечное число, отличное от нуля, значит, полученный ряд сходится вместе с рядом 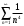 . .Значит полученный ряд сходится. Следовательно, исходный ряд сходится абсолютно в точке 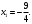 б) Исследуем сходимость ряда в точке 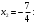 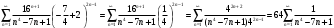 Как показано выше полученный ряд сходится. Следовательно, исходный ряд сходится абсолютно в точке  Таким образом, областью сходимости ряда является промежуток 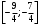 ; областью абсолютной сходимости – интервал ; областью абсолютной сходимости – интервал 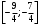 . . Задача 6. Пользуясь признаком Вейерштрасса, докажите равномерную сходимость данного ряда на указанном промежутке. 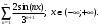 Решение:для любого 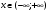 и для всех и для всех  справедливо неравенство: справедливо неравенство: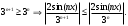 Так как 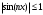 , то: , то: 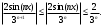 Таким образом, на интервале 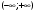 геометрическая прогрессия геометрическая прогрессия 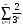 мажорирует функциональный ряд мажорирует функциональный ряд 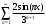 , следовательно, по признаку Вейерштрасса он равномерно сходится в данном промежутке. , следовательно, по признаку Вейерштрасса он равномерно сходится в данном промежутке.Задача 7. Разложите функцию f(x) в ряд Тейлора по степеням 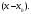 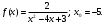 Решение: Разложение в ряд Тейлора определяется формулой:  Найдем значения функции и ее производных при   Подставляя полученные значения производных в формулу ряда Тейлора, получим:  Задача 8. Вычислите интеграл, разложив подынтегральную функцию в ряд Маклорена. Укажите количество членов числового ряда, полученного после интегрирования степенного ряда, необходимое для достижения точности вычислений с погрешностью 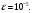 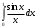 Решение: Разложим подынтегральную функцию в ряд Маклорена. 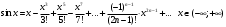 Тогда 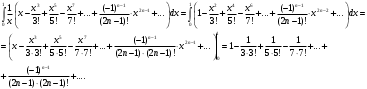 Полученный числовой ряд знакочередующийся и, согласно теореме Лейбница, остаток ряда, взятый по модулю, не превосходит модуля первого отбрасываемого члена. Таким образом, абсолютная погрешность будет меньше, чем первый отбрасываемый член, взятый по модулю, т.е. 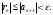 В нашем случае неравенство В нашем случае неравенство 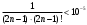 справедливо справедливо 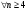 . Тогда указанная точность достигается уже при n 4, значит, . Тогда указанная точность достигается уже при n 4, значит,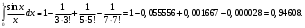 Задача 9. Вычислите предел, используя разложение элементарных функций в ряд Маклорена. 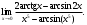 Решение: Разложим элементарные функции в ряд Маклорена. 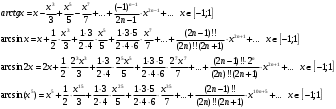  Задача 10.Разложите функцию 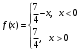 в тригонометрический ряд Фурье на интервале 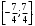 Решение: В данной задаче период разложения  полупериод полупериод  Ряд Фурье имеет вид:  где   Используя соответствующие формулы, вычислим коэффициенты Фурье:    При четных n: 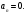 При нечетных n: 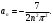 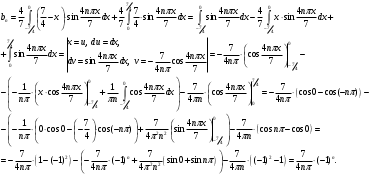 Искомое разложение имеет вид: 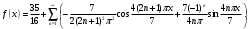 Задача 11. Разложите функцию 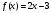 в тригонометрический ряд Фурье по синусам на интервале в тригонометрический ряд Фурье по синусам на интервале 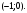 Решение: В данной задаче период разложения 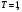 полупериод полупериод 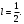 Разложение функции в ряд Фурье по синусам имеет вид:  где   Используя соответствующие формулы, вычислим коэффициенты Фурье:    Искомое разложение имеет вид:  Задача 12. Найдите синус-преобразование Фурье  функции функции  Решение: Синус-преобразование Фурье имеет вид:  Вычислим:    Индивидуальная практическая работа ИПР3-2 Вариант 27 Задача 1. Постройте на комплексной плоскости область D, заданную системой неравенств. Проверьте, принадлежит ли заданная точка  области D. области D. Решение: Преобразуем для удобства функции комплексной переменной:  Получили 2 окружности на комплексной плоскости: 1) с центром в (-1; 0) и радиусом 1: 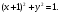 2) с центром в (2; 0) и радиусом 3: 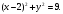 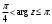 Изобразим область D.  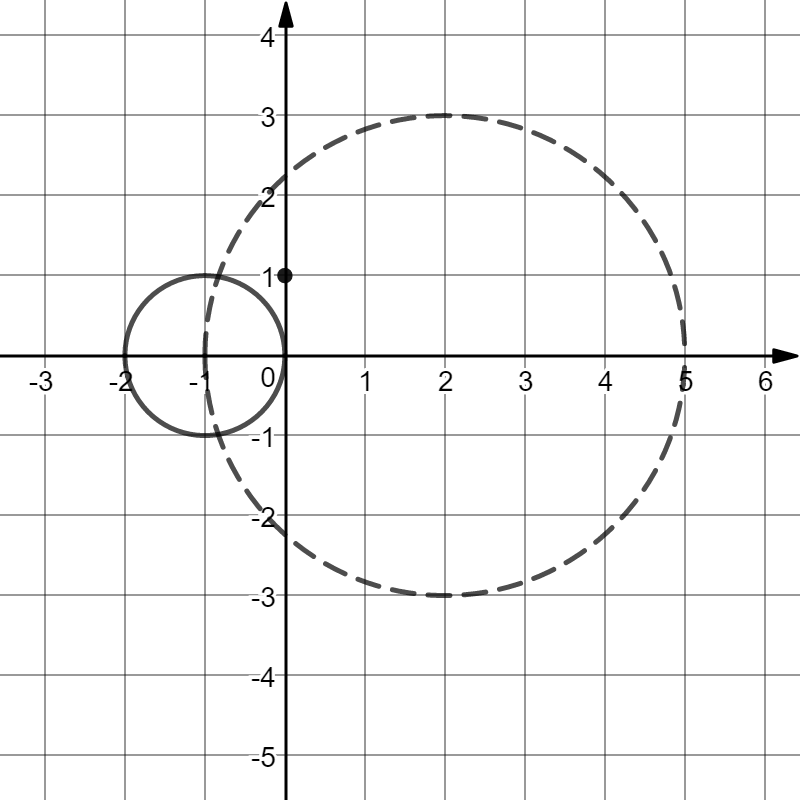 z0         Для того чтобы установить, принадлежит ли точка 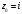 области D, проверим, выполняются ли для нее неравенства области D, проверим, выполняются ли для нее неравенства 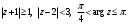 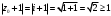 – верно, – верно,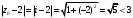 – верно, – верно,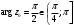 – верно. – верно. Таким образом, 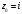 принадлежит области D. принадлежит области D.И из рисунка видно, что заданная точка 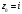 принадлежит области D. принадлежит области D.Задача 2. Определите область (круг) сходимости данного комплексного ряда. Исследуйте его сходимость (сходится абсолютно, сходится условно, расходится) в точках 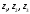 . .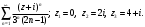 Решение: Воспользуемся признаком Даламбера: 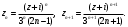 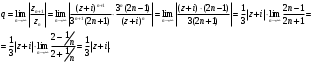 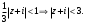 Получили, что ряд сходится в круге 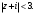 а) Исследуем сходимость ряда в точке 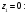 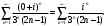 Используем признак Лейбница: 1) 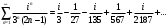 Ряд является знакочередующимся. 2) 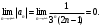 Члены ряда убывают по модулю, начиная с некоторого номера n, при этом, каждый следующий член ряда по модулю меньше, чем предыдущий, таким образом, убывание монотонно. Значит полученный ряд сходится. Следовательно, исходный ряд сходится абсолютно в точке 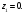 б) Исследуем сходимость ряда в точке 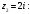 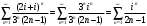 Используем признак Лейбница: 1) 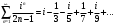 Ряд является знакочередующимся. 2) 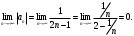 Члены ряда убывают по модулю, начиная с некоторого номера n, при этом, каждый следующий член ряда по модулю меньше, чем предыдущий, таким образом, убывание монотонно. Значит полученный ряд сходится. Следовательно, исходный ряд сходится абсолютно в точке 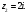 в) Исследуем сходимость ряда в точке 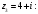 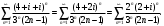 Воспользуемся признаком Даламбера: 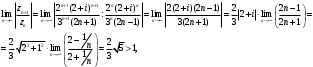 значит ряд расходится. Следовательно, исходный ряд сходится условно в точке 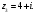 Задача 3. Проверьте, является ли функция 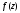 аналитической в области D. Вычислите интеграл от этой функции по указанной кривой L. аналитической в области D. Вычислите интеграл от этой функции по указанной кривой L.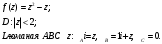 Решение: Найдем действительную и мнимую части функции: 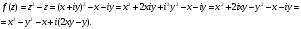 Получаем: 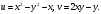 Найдем частные производные: 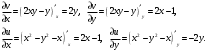 Проверим выполнение условия Коши-Римана: 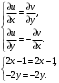 Условия выполнены для любой точки 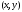 , значит функция , значит функция 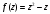 является аналитичной на всей области является аналитичной на всей области 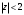 . .Изобразим область на комплексной плоскости:     A C B Область интегрирования – ломанная 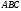 . .На AB: 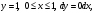 на BC: на BC: 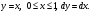 Интеграл от комплексной функции по кривой вычисляется по следующей формуле: 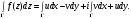 Вычислим интеграл: 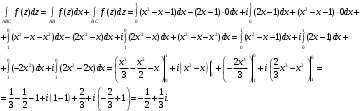 Задача 4. Функция 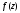 разложена в ряд Лорана в окрестности своей изолированной особой точки разложена в ряд Лорана в окрестности своей изолированной особой точки 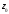 , где , где 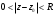 А) Определите тип особой точки 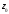 и найдите в ней вычет функции и найдите в ней вычет функции 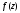 . .Б) Вычислите с помощью вычетов интеграл 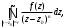 если если 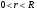 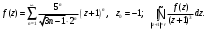 Решение: А) Общий вид лорановского разложения имеет вид: 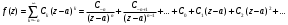 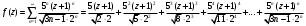 Особая точка 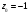 является устранимой особой точкой, так как в разложении отсутствует главная часть. является устранимой особой точкой, так как в разложении отсутствует главная часть.Для устранимой особой точки вычет равен: 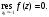 Б) Как известно, коэффициенты ряда Лорана для функции 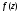 в указанной окрестности в указанной окрестности 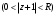 можно найти по формулам можно найти по формулам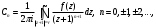 где 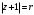 – произвольная окружность с радиусом r R. – произвольная окружность с радиусом r R.Отсюда следует, что 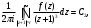 т.е. т.е. 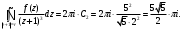 Задача 5. Найдите все лорановские разложения функции 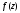 по степеням по степеням 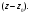 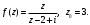 Решение: Особой точкой функции является точка 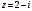 . Проведем окружность с центром . Проведем окружность с центром 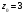 , проходящую через , проходящую через 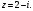 Следовательно, имеется 2 области: а) 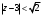 ; разложение в этой области – это разложение в ряд Тейлора, поскольку ; разложение в этой области – это разложение в ряд Тейлора, поскольку 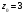 не особая точка; не особая точка;б) 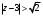 : разложение в этой области – разложение в ряд Лорана в окрестности бесконечно удаленной точки. : разложение в этой области – разложение в ряд Лорана в окрестности бесконечно удаленной точки.Найдем эти разложения. Преобразуем функцию 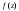 : :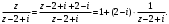 а) Разложение 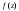 в в 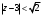 . .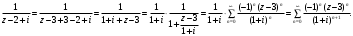 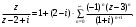 Это разложение является рядом Тейлора функции 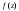 . Область сходимости полученного ряда . Область сходимости полученного ряда  . .б) Разложение  в в  . . 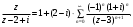 Область сходимости полученного ряда 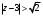 . .Задача 6. Дана функция 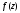 . Найдите её изолированную особую точку . Найдите её изолированную особую точку 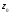 и разложите функцию в ряд Лорана в окрестности точки и разложите функцию в ряд Лорана в окрестности точки 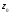 . С помощью вычетов найдите интегралы . С помощью вычетов найдите интегралы 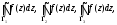 где где 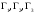 – заданные контуры. – заданные контуры. 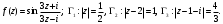 Решение: Изолированной особой точкой является  Разложим функцию в ряд Лорана в окрестности точки  : :  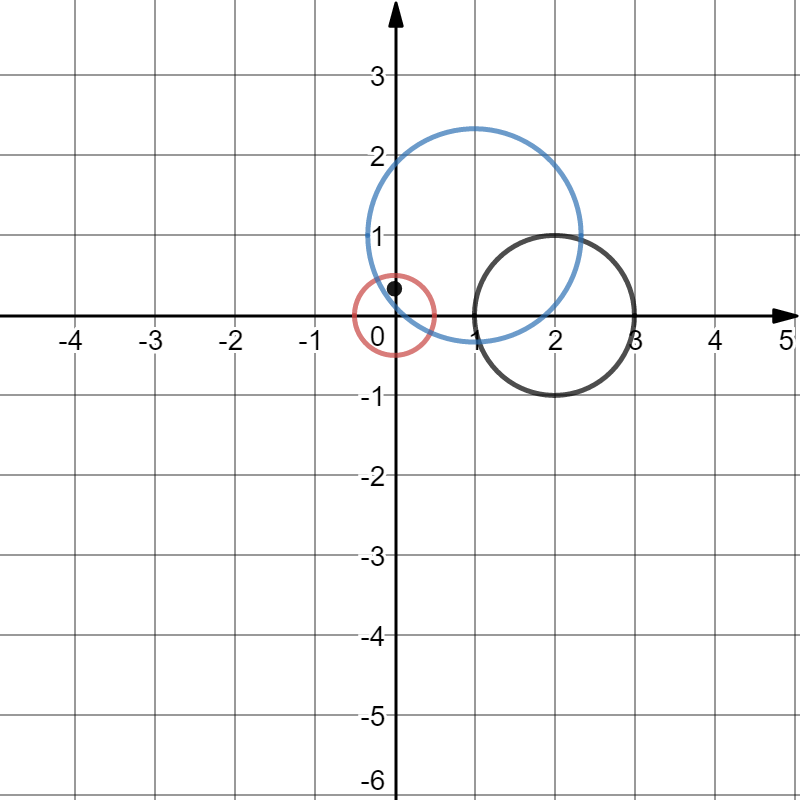 Г2 Г1 Г3 z0 Особая точка лежит вне контура 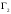 , подынтегральная функция аналитична, и интеграл равен нулю , подынтегральная функция аналитична, и интеграл равен нулю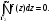 Особая точка лежит в кругах 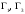 , вычислим интеграл с использованием вычетов. , вычислим интеграл с использованием вычетов.Особая точка 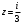 является существенно особой точкой, так как в разложениях главная часть содержит бесконечное число членов, т.е. имеется бесконечное число членов с отрицательными степенями. является существенно особой точкой, так как в разложениях главная часть содержит бесконечное число членов, т.е. имеется бесконечное число членов с отрицательными степенями.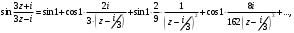 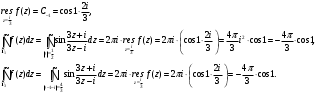 Задача 7. Вычислите интеграл с помощью интегральной формулы Коши. Направление обхода контура – положительное. 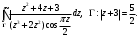 Решение: Подынтегральная функция аналитическая всюду за исключением нулей знаменателя 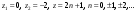 . В круге интегрирования находятся точки . В круге интегрирования находятся точки 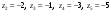 . Преобразуем подынтегральную функцию . Преобразуем подынтегральную функцию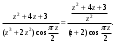 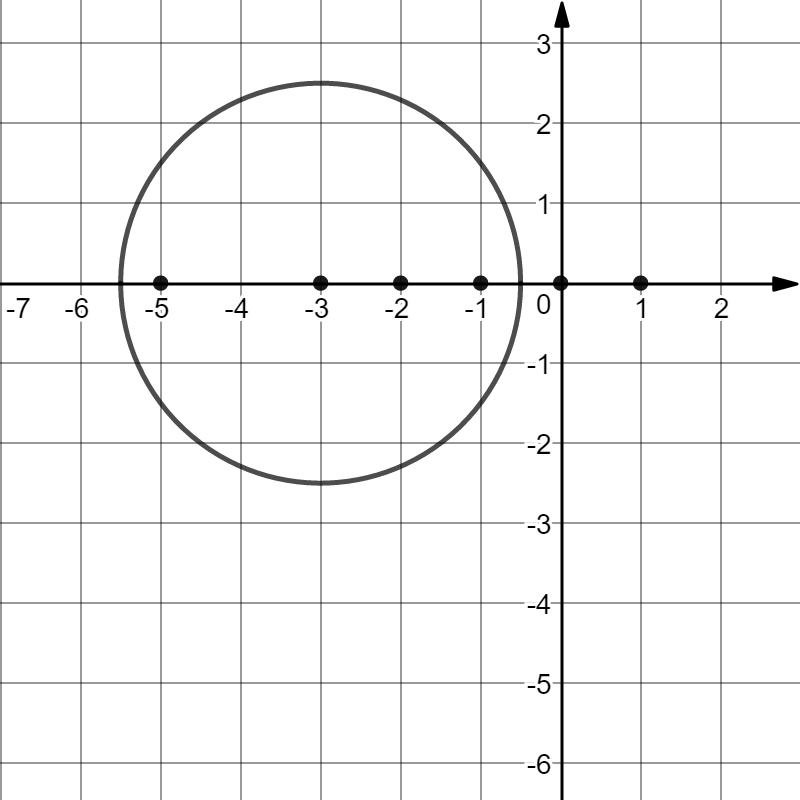 z2 z4 z5 z3 Функция 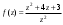 аналитическая в круге аналитическая в круге 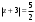 . Поэтому, пользуясь интегральной формулой Коши, найдем . Поэтому, пользуясь интегральной формулой Коши, найдем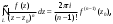 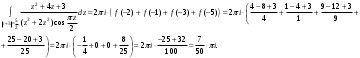 Задача 8. Найдите изображение заданного оригинала. 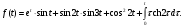 Решение: Вычислим интеграл, заданный в оригинале: 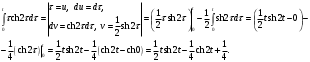 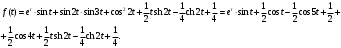 Перейдем от оригиналов к изображениям: 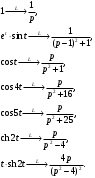 Запишем полученное изображение: 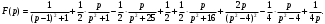 Задача 9. Найдите оригинал по заданному изображению. 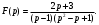 Решение: Представим данную дробь в виде суммы простейших рациональных дробей: 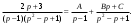 Приведя сумму дробей в правой части равенства к общему знаменателю, приравняем числители дробей: 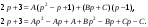 Приравняв коэффициенты при одинаковых степенях, получим систему уравнений для определения коэффициентов A, B, C: 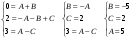 Следовательно, 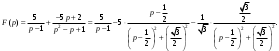 Перейдем от изображений к соответствующим оригиналам: 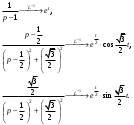 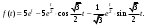 Задача 10. Решите дифференциальное уравнение операционным методом.  Решение: Перейдем от оригиналов к изображениям:  Операторное уравнение примет вид  Откуда получаем операторное решение  Представим последнюю дробь в виде суммы простейших дробей: 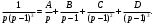 Воспользуемся методом неопределенных коэффициентов. 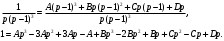 Составляем систему: 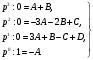 Найдем решение полученной системы. 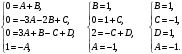 Подставляя найденные коэффициенты, получим 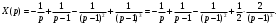 Перейдем к оригиналам 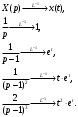 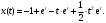 Ответ: 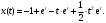 |
