Матанализ. матанализ. 1. Сходимость и сумма числового ряда Пусть мы имеем числовую последовательность, где
 Скачать 321.92 Kb.
|
|
Билет 1 1.Сходимость и сумма числового ряда Пусть мы имеем числовую последовательность  , где Числовой ряд – это сумма членов числовой последовательности вида 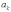  называют общим членом числового ряда или k–ым членом ряда.Частичная сумма числового ряда – это сумма вида  где n – некоторое натуральное число. называют также n-ой частичной суммой числового ряда. Частичные суммы  образуют бесконечную последовательность частичных сумм числового ряда.Числовой ряд  называется сходящимся, если существует конечный предел последовательности частичных сумм  . Если предел последовательности частичных сумм числового ряда не существует или бесконечен, то ряд называется расходящимся.Суммой сходящегося числового ряда называется предел последовательности его частичных сумм, то есть,  Необходимое условие сходимости ряда Если ряд сходится, то предел его k-того члена равен нулю :  2.Первообразная и неопределенный интеграл Функция F(x) называется первообразной для функции y=f(x) на промежутке (a;b), конечном или бесконечном, если функция F(x) дифференцируема в каждой точке этого промежутка и ее производная удовлетворяет следующему равенству: F′(x)=f(x) Последнее равенство можно записать через дифференциалы: 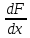 =f(x) или dF=f(x)dxТеорема о бесконечном множестве первообразных для функции Если функция F(x) является первообразной для функции y=f(x) на некотором промежутке, то и функция Φ(x)=F(x)+C, где C - произвольная постоянная, также будет первообразной для функции f(x) на рассматриваемом промежутке. Таким образом, если функция y=f(x) имеет первообразную, то она имеет бесконечное множество первообразных. Теорема об общем виде первообразной для функции Если функции F(x) и Φ(x) - две любые первообразные функции y=f(x), то их разность равна некоторой постоянной, то есть  Последнюю теорему можно сформулировать иначе: каждая функция, которая является первообразной для функции f(x), может быть представлена в виде F(x)+C. Билет 2 1.Свойства сходящихся рядов 1)Если сходится числовой ряд , то сходящимся будет и ряд . Другими словами, сходящимся будет и ряд без первых m членов. Если к сходящемуся числовому ряду добавить несколько членов (от первого до m-ого), то полученный ряд также будет сходящимся.2)Если сходится числовой ряд и его сумма равна S, то сходящимся будет и ряд  , причем , где A – произвольная постоянная.Если сходятся числовые ряды и  , их суммы равны A и B соответственно, то сходящимися будут ряды  и  , причем их суммы будут равны A + B и A - B соответственно.2.Таблица интегралов Билет 3 1.Критерий Коши сходимости ряда  2. Метод замены переменной для неопределенных интегралов Билет 4 1.Интегральный признак сходимости ряда Пусть - положительный числовой ряд. Составим функцию непрерывного аргумента y = f(x), аналогичную функции  . Пусть функция y = f(x) положительная, непрерывная и убывающая на интервале  , где ). Тогда в случае сходимости несобственного интеграла  сходится исследуемый числовой ряд. Если же несобственный интеграл расходится, то исходный ряд тоже расходится.2.Метод интегрирования по частям для неопределенных интегралов Формула интегрирования по частям в неопределенном интеграле Для применения формулы интегрирования по частям подынтегральное выражение нужно разбить на два множителя. Один из них обозначается через u, а остальная часть относится ко второму множителю и обозначается через dv. Затем дифференцированием находится du и интегрированием - функция v. При этом за u следует брать такую часть подынтегральной функции, которая при дифференцировании сильно не усложняется, а за dv - такую часть подынтегрального выражения, которая легко интегрируется. Данный метод интегрирования используют тогда, когда подынтегральная функция содержит :  - логарифмические функции, а также обратные тригонометрические функции (с приставкой "arc"), тогда на основании продолжительного опыта интегрирования по частям эти функции обозначаются через u;, , - синус, косинус и экспоненту, умноженные на P(x) - произвольный многочлен от икса, тогда эти функции обозначают через dv, а многочлен - через u; , , , , в этом случае интегрирование по частям применяется дважды. Смысл формулы интегрирования по частям состоит в том, чтобы в результате её применения новый интеграл оказался табличным или хотя бы стал проще первоначального. Билет 5 1.Обобщенный гармонический ряд Сумма вида  называется гармоническим числовым рядом.Сумма вида  , где s – некоторое действительное число, называется обобщенно гармоническим числовым рядом.ОБОБЩЕННО ГАРМОНИЧЕСКИЙ РЯД  СХОДИТСЯ ПРИ s > 1 И РАСХОДИТСЯ ПРИ .Доказательство. Для s = 1 получим гармонический ряд  , а выше мы установили его расходимость.При s < 1 справедливо неравенство  для всех натуральных k. В силу расходимости гармонического ряда можно утверждать, что последовательность его частичных сумм неограниченна (так как не существует конечного предела). Тогда последовательность частичных сумм числового ряда тем более неограниченна (каждый член этого ряда больше соответствующего члена гармонического ряда), следовательно, обобщенно гармонический ряд расходится при s < 1.Доказательство сходимости ряда при s > 1.Запишем разность 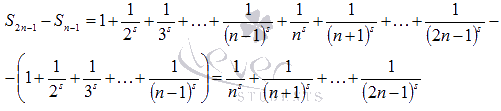 : Очевидно, что 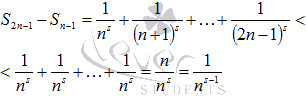 , тогда 2.Интегрирование рациональных функций Рациональная функция - это дробь вида , числитель и знаменатель которой - многочлены или произведения многочленов. Алгоритм интегрирования рациональных функций Шаг 1. Определить вид многочлена в знаменателе дроби (он может иметь действительные, кратные действительные, комплексные и кратные комплексные корни) и в зависимости от вида разложить дробь на простые дроби, в числителях которых - неопределённые коэффициенты, число которых равно степени знаменателя. Шаг 2. Определить значения неопределённых коэффициентов. Для этого потребуется решить систему уравнений, сводящуюся к системе линейных уравнений. Шаг 3. Найти интеграл исходной рациональной функции (дроби) как сумму интегралов полученных простых дробей, к которым применяются табличные интегралы. Шаг 1 Многочлен в знаменателе имеет действительные корни. То есть, в знаменателе имеет место цепочка сомножителей вида  , в которой каждый из сомножителей находится в первой степени. В этом случае разложение дроби с использованием метода неопределённых коэффициентов будет следующим: Многочлен в знаменателе имеет кратные действительные корни. Этот случай имеет место, когда в цепочке сомножителей в знаменателе присутствует выражение вида , то есть один из многочленов в степени 2 и больше. В этом случае разложение дроби с использованием метода неопределённых коэффициентов будет следующим: 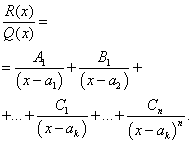 Многочлен в знаменателе имеет комплексные корни: дискриминант квадратного уравнения , присутствующего в цепочке сомножителей в знаменателе, меньше нуля. В этом случае при разложении дроби в простой дроби, соответствующей описанному выше сомножителю, в числителе нужно записывать линейное выражение с переменной x (это выражение - последнее в следующей записи):  Шаг 2 На первом шаге мы представили подынтегральные дроби в виде суммы дробей с неопределёнными коэффициентами. В начале этого шага потребуется привести полученную сумму дробей к общему знаменателю. После этого в их числителях будут произведения неопределённых коэффициентов на многочлены, которых нет в данной отдельной дроби, но которые есть в других полученных дробях. Полученное таким образом выражение приравнивается к числителю исходной дроби. Затем составляется система из уравнений, в которых степени икса одинаковы. Путём решения системы и находятся неопределённые коэффициенты. Для решения достаточно знать, как системы уравнений решаются методом подстановки и методом сложения. Шаг 3 Полученные простые дроби и интегрировать проще. К исходной сумме дробей применяется правило интеграла суммы (интеграл суммы равен сумме интегралов) и табличные интегралы. Чаще всего требуется применять табличные интегралы, приводящие к натуральному логарифму и арктангенсу. Билет 6 1.Ряд геометрической прогрессии Это ряд:  где - некоторое число, q – знаменатель геометрической прогрессии. Как известно, сумма первых n членов геометрической прогрессии находится по формуле:  Найдем предел этой суммы:  Рассмотрим следующие случаи в зависимости от величины q: 1) |q|<1, то  , поэтому , т.е. ряд сходится и его сумма равна . 2) |q|>1, то  , поэтому и ряд расходится.3) |q|=1, то при q=1 ряд принимает вид  и , ряд расходится. При q=-1 ряд принимает вид  . Следовательно, не существует и ряд расходится. Вывод: ряд геометрической прогрессии сходится при |q|<1, и расходится при 2.Определение интеграла Римана Рассмотрим функцию y = f(x), которая определена на отрезке [a; b]. Разобьем отрезок [a; b] на n частей  точками  .Обозначим  , а точки  будем выбирать так, чтобы при . Внутри каждого отрезка выберем точку .При озвученных условиях существует множество способов выбора точек и  .Интегральной суммой функции y = f(x) для данного разбиения отрезка [a; b] и данного выбора точек 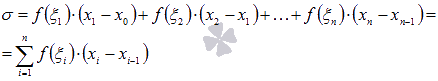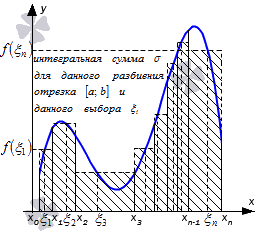называют выражение  Для конкретного разбиения отрезка [a; b] и выбора точек мы получим свою интегральную сумму. То есть, мы имеем множество интегральных сумм для различных вариантов выбора и .Число I называется пределом интегральных сумм при , если для любого сколь угодно малого положительного ипсилон > 0 существует такое сколь угодно малое положительное, зависящее от ипсилон, дельта > 0 , что как только , то при любом выборе точек справедливо неравенство .Функция y = f(x) называется интегрируемой на отрезке [a; b], если существует конечный предел ее интегральных сумм при . Значение предела есть определенный интеграл Римана. Принято следующее обозначение интеграла Римана:  . Тогда по определению определенного интеграла Римана имеем  .Числа a и b называются нижним и верхним пределом интегрирования соответственно, f(x) называется подынтегральной функцией, x – переменной интегрирования. Значение определенного интеграла Римана не зависит от переменной интегрирования, то есть, 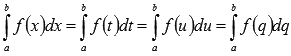 .Билет 7 1.Первый признак сравнения для рядов с неотрицательными членами Пусть и - два положительных числовых ряда и выполняется неравенство  для всех k = 1, 2, 3, ... Тогда из сходимости ряда следует сходимость , а из расходимости ряда следует расходимость .Первый признак сравнения используется очень часто и представляет собой очень мощный инструмент исследования числовых рядов на сходимость. Основную проблему представляет подбор подходящего ряда для сравнения. Ряд для сравнения обычно (но не всегда) выбирается так, что показатель степени его k-ого члена равен разности показателей степени числителя и знаменателя k-ого члена исследуемого числового ряда. К примеру, пусть  , разность показателей степени числителя и знаменателя равна 2 – 3 = -1, поэтому, для сравнения выбираем ряд с k-ым членом  , то есть, гармонический ряд. 2.Интегральные суммы Дарбу Пусть на отрезке [a,b] задана ограниченная функция . Введем разбиение Пусть  Наряду с интегральными суммами 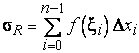 рассмотрим суммы 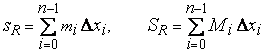 которые называют нижней и верхней суммами Дарбу. Очевидно, что . Суммы Дарбу не обязательно являются интегральными суммами. Однако, если f(x)- непрерывная функция, то и являются, соответственно, наименьшей и наибольшей из интегральных сумм, отвечающих данному разбиению, так как по теореме Вейерштрасса f(x) достигает минимума и максимума в каждом , и поэтому можно выбрать точки , так, что и . Так как  и , то(1) При фиксированном разбиении и - постоянные числа, а интегральная сумма остается переменной в силу произвольности чисел . Легко видеть, что за счет выбора точек сумму можно сделать как угодно близкой к и , т. е. при данном разбиении и являются точной нижней и точной верхней гранями для интегральных сумм: 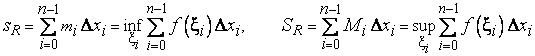 Пусть - разбиения . Если же точки принадлежат , то будем писать и говорить, что есть продолжение . Если множество точек, из которых состоит , есть теоретико-множественная сумма множеств точек, из которых состоят и , то будем писать Билет 8 1.Второй признак сравнения для рядов с неотрицательными членами Пусть и - положительные числовые ряды. Если  , то из сходимости ряда следует сходимость . Если  , то из расходимости числового ряда следует расходимость .Следствие. Если и , то из сходимости одного ряда следует сходимость другого, а из расходимости следует расходимость.Исследуем ряд 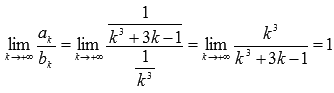 на сходимость с помощью второго признака сравнения. В качестве ряда возьмем сходящийся ряд  . Найдем предел отношения k-ых членов числовых рядов: Таким образом, по второму признаку сравнения из сходимости числового ряда следует сходимость исходного ряда.2.Основные свойства интегрируемых функций и интеграла Римана 1) Для функции y = f(x), определенной при x = a, справедливо равенство 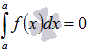 То есть, значение определенного интеграла с совпадающими пределами интегрирования равно нулю. Это свойство является следствием определения интеграла Римана, так как в этом случае каждая интегральная сумма для любого разбиения промежутка [a; a] и любого выбора точек равна нулю, так как  , следовательно, пределом интегральных сумм является ноль.2) Для интегрируемой на отрезке [a; b] функции выполняется 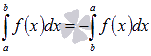 Другими словами, при перемене верхнего и нижнего пределов интегрирования местами значение определенного интеграла меняется на противоположное. Это свойство определенного интеграла также следует из понятия интеграла Римана, только нумерацию разбиения отрезка следует начинать с точки x = b. 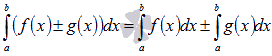 для интегрируемых на отрезке [a; b] функций y = f(x) и y = g(x).4)Постоянный множитель можно выносить за знак определенного интеграла. То есть, для интегрируемой на отрезке [a; b] функции y = f(x) и произвольного числа k справедливо равенство 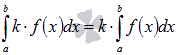 5)Пусть функция y = f(x) интегрируема на интервале X, причем  и , тогда  6)Если функция интегрируема на отрезке [a; b], то она интегрируема и на любом внутреннем отрезке  .7)Если функция y = f(x) интегрируема на отрезке [a; b] и  для любого значения аргумента  , то  Свойства интеграла Римана Теорема1. 1) Если , то , и при этом  2) Если , , то , и при этом Свойства интеграла 1) и 2) называется линейностью интеграла Римана. Аддитивность интеграла Римана. Теорема 1. Пусть . Тогда тогда и только тогда, когда Одновременно и . При этом  Теорема 2. Пусть и отличаются лишь в конечном числе точек. Тогда и в том случае, когда они интегрируемы, интегралы их равны: Монотонность интеграла Римана. Теорема 1. Пусть и для любого . Тогда Билет 9 1.Третий признак сравнения 2х рядов с неотрицательными числами Пусть и - положительные числовые ряды. Если с некоторого номера N выполняется условие  , то из сходимости ряда следует сходимость , а из расходимости ряда следует расходимость .2.Теоремы о среднем для интегралов Если f(x) - непрерывная функция, заданная на промежутке [a, b], то существует такая точка   , что   (1)В самом деле, пусть M и m наибольшее и наименьшее значения f(x) на промежутке [a, b]. Составим для f(x) какую-нибудь интегральную сумму    Так как при всех k будет m ≤ f(ξk) ≤ M, а xk+1 > xk, то m(xk+1 - xk) ≤ M(xk+1 - xk). Складывая такие неравенства и замечая, что    получим: m(b - a) ≤ σ ≤ M(b - a).Переходя в этом неравенстве к пределу при λ → 0, приходим после деления на b - a к новому неравенству    Таким образом, частное  есть число, лежащее между наибольшим и наименьшим значениями непрерывной функции. Как известно, тогда и само это число должно являться одним из значений той же функции. Поэтому в [a, b] обязательно существует такая точка ξ, что h = f(ξ), а это равносильно равенству (1) Заметим, что равенство (1) справедливо не только при a < b, но и при a = b (тогда обе части этого равенства нули), а также и при a > b (этот случай приводится к рассмотренному изменением знаков). В первом из этих случаев будет ξ = a, а во втором a ≥ ξ ≥ b. Билет 10 1.Признак Даламбера сходимости рядов Пусть - положительный числовой ряд. Если  , то числовой ряд сходится, если  , то ряд расходится.Замечание. Признак Даламбера справедлив, если предел бесконечен, то есть, если  , то ряд сходится, если  , то ряд расходится.Если  , то признак Даламбера не дает информацию о сходимости или расходимости ряда и требуется дополнительное исследование.2.Основные свойства интеграла Римана (см билет 8 в. 2) Билет 11 1.Признак Коши сходимости рядов Радикальный признак Коши: Рассмотрим положительный числовой ряд . Если существует предел: , то: а) При D<1 ряд сходится. В частности, ряд сходится при D=0. б) При D>1 ряд расходится. В частности, ряд расходится при . в) При D=1 признак не дает ответа. Радикальный признак Коши обычно использует в тех случаях, когда корень «хорошо» извлекается из общего члена ряда. Как правило, этот перец находится в степени, которая зависит от n . Есть еще другие случаи интегральный признак Коши Рассмотрим положительный числовой ряд . Если существует несобственный интеграл , то ряд сходится или расходится вместе с этим интегралом. 2.Формула Ньютона-Лейбница Пусть функция y=f(x) имеет первообразную F(x) на отрезке [a; b], причем значение первообразной в точке x=a равно нулю: F(a)=0. Определенным интегралом Ньютона-Лейбница называется значение этой первообразной в точке b, то есть,  при F(a)=0.Это определение тесно связано с формулой Ньютона-Лейбница  В формуле Ньютона-Лейбница F(x) – любая первообразная из их множества, а в понятии определенного интеграла Ньютона-Лейбница фигурирует именно та первообразная, которая обращается в ноль при x=a. Билет 12 1.Признак Лейбница сходимости ряда Если абсолютные величины членов знакочередующегося ряда монотонно убывают  и предел модуля общего члена ряда равен нулю при , то ряд сходится.2.Замена переменной в определенном интеграле (см в лекциях) Билет 13 1.Оценка остатка знакочередующегося ряда Теорема 11. (Об оценке остатка знакочередующегося числового ряда) Если знакочередующийся числовой ряд сходится по признаку Лейбница, то его n-й остаток по абсолютной величине не превосходит модуля (n+1)-го члена ряда. Доказательство. Пусть ряд u1-u2+u3-u4+…+(-1)n-1.un+… сходится по признаку Лейбница. Тогда n-й остаток ряда Rn=±(un+1-un+2+un+3-…) сам является суммой знакочередующегося числового ряда и по теореме Лейбница |Rn|≤|un+1|. Теорема доказана. 2.Формула интегрирования по частям для определенного интеграла (см в лекциях) Билет 14 1.Абсолютно и условно сходящиеся ряды Абсолютная сходимость Ряд  называется абсолютно сходящимся, если ряд  также сходится. Если ряд сходится абсолютно, то он является сходящимся (в обычном смысле). Обратное утверждение неверно.Условная сходимость Ряд называется условно сходящимся, если сам он сходится, а ряд, составленный из модулей его членов, расходится.2.Определение несобственных интегралов Что значит вычислить несобственный интеграл? Вычислить несобственный интеграл – это значит, найти ЧИСЛО (точно так же, как в определенном интеграле), или доказать, что он расходится (то есть, получить в итоге бесконечность вместо числа). Несобственные интегралы бывают двух видов. Несобственный интеграл с бесконечным пределом (ами) интегрирования Иногда такой несобственный интеграл называют несобственным интегралом первого рода. В общем виде несобственный интеграл с бесконечным пределом чаще всего выглядит так: В отличие от определенного интеграла в верхнем пределе он бесконечный: . Несобственные интегралы от неограниченных функций Или несобственные интегралами второго рода. Несобственные интегралы второго рода похожи на обычный определенный интеграл , но в отличие от определенного интеграла, подынтегральная функция терпит бесконечный разрыв (не существует): 1) в точке , 2) или в точке , 3) или в обеих точках сразу, 4) или даже на отрезке интегрирования. |