|
|
задача. Задача к кр. Задача к кр остроение
Задача к кр
остроение мультипликативной модели временного ряда.
Общий вид мультипликативной модели следующий:
Y = T x S x E
Эта модель предполагает, что каждый уровень временного ряда может быть представлен как произведение трендовой (T), сезонной (S) и случайной (E) компонент.
Рассчитаем компоненты мультипликативной модели временного ряда.
Шаг 1. Проведем выравнивание исходных уровней ряда методом скользящей средней. Для этого:
1.1. Найдем скользящие средние (гр. 3 таблицы). Полученные таким образом выровненные значения уже не содержат сезонной компоненты.
1.2. Приведем эти значения в соответствие с фактическими моментами времени, для чего найдем средние значения из двух последовательных скользящих средних – центрированные скользящие средние (гр. 4 табл.).
t
|
yt
|
Скользящая средняя
|
Центрированная скользящая средняя
|
Оценка сезонной компоненты (стлб.2 / стлб.4)
|
1
|
5486789
|
-
|
-
|
-
|
2
|
6556599
|
5513197.5
|
-
|
-
|
3
|
7854524
|
4778680.5
|
5145939
|
1.526
|
4
|
2154878
|
5325921.25
|
5052300.875
|
0.427
|
5
|
2548721
|
4166451.75
|
4746186.5
|
0.537
|
6
|
8745562
|
6091835.5
|
5129143.625
|
1.705
|
7
|
3216646
|
6058602
|
6075218.75
|
0.529
|
8
|
9856413
|
4410918.5
|
5234760.25
|
1.883
|
9
|
2415787
|
5254203.75
|
4832561.125
|
0.5
|
10
|
2154828
|
5170440.25
|
5212322
|
0.413
|
11
|
6589787
|
5377930.5
|
5274185.375
|
1.249
|
12
|
9521359
|
7038587.5
|
6208259
|
1.534
|
13
|
3245748
|
7854782.25
|
7446684.875
|
0.436
|
14
|
8797456
|
7388189.75
|
7621486
|
1.154
|
15
|
9854566
|
6576752.75
|
6982471.25
|
1.411
|
16
|
7654989
|
4377388.75
|
5477070.75
|
1.398
|
17
|
|
1913747.25
|
3145568
|
0
|
18
|
|
0
|
956873.625
|
0
|
19
|
|
-
|
-
|
-
|
20
|
|
-
|
-
|
-
|
Шаг 2. Найдем оценки сезонной компоненты как частное от деления фактических уровней ряда на центрированные скользящие средние (гр. 5 табл.). Эти оценки используются для расчета сезонной компоненты S. Для этого найдем средние за каждый период оценки сезонной компоненты Sj. Сезонные воздействия за период взаимопогашаются. В мультипликативной модели это выражается в том, что сумма значений сезонной компоненты по всем кварталам должна быть равна числу периодов в цикле. В нашем случае число периодов одного цикла равно 4.
Показатели
|
1
|
2
|
3
|
4
|
1
|
-
|
-
|
1.526
|
0.427
|
2
|
0.537
|
1.705
|
0.529
|
1.883
|
3
|
0.5
|
0.413
|
1.249
|
1.534
|
4
|
0.436
|
1.154
|
1.411
|
1.398
|
5
|
0
|
0
|
-
|
-
|
Всего за период
|
1.473
|
3.273
|
4.717
|
5.241
|
Средняя оценка сезонной компоненты
|
0.368
|
0.818
|
1.179
|
1.31
|
Скорректированная сезонная компонента, Si
|
0.401
|
0.89
|
1.283
|
1.426
|
Для данной модели имеем:
0.368 + 0.818 + 1.179 + 1.31 = 3.676
Корректирующий коэффициент: k=4/3.676 = 1.088
Рассчитываем скорректированные значения сезонной компоненты Si и заносим полученные данные в таблицу.
Шаг 3. Разделим каждый уровень исходного ряда на соответствующие значения сезонной компоненты. В результате получим величины T x E = Y/S (гр. 4 табл.), которые содержат только тенденцию и случайную компоненту.
Находим параметры уравнения методом наименьших квадратов.
Система уравнений МНК:
a0n + a1∑t = ∑y
a0∑t + a1∑t2 = ∑y*t
Для наших данных система уравнений имеет вид:
20a0 + 210a1 = 105586458.35
210a0 + 2870a1 = 876252203.43
Из первого уравнения выражаем а0 и подставим во второе уравнение
Получаем a1 = -80978.975, a0 = 6129602.155
Среднее значение
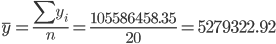
t
|
y
|
t2
|
y2
|
t*y
|
y(t)
|
(yi-y)2
|
(y-y(t))2
|
1
|
13693845.765
|
1
|
1.8752141182591E+14
|
13693845.765
|
6048623.18
|
70804194745925
|
58449428372839
|
2
|
7363816.89
|
4
|
54225799182668
|
14727633.779
|
5967644.205
|
4345115119663.3
|
1949298165731.2
|
3
|
6121141.516
|
9
|
37468373461444
|
18363424.549
|
5886665.23
|
708658553208.85
|
54979128896.698
|
4
|
1511384.407
|
16
|
2284282825051.4
|
6045537.627
|
5805686.255
|
14197360620232
|
18441028361958
|
5
|
6361059.678
|
25
|
40463080230603
|
31805298.391
|
5724707.28
|
1170154419717.2
|
404944375013.49
|
6
|
9822274.805
|
36
|
96477082344720
|
58933648.83
|
5643728.305
|
20638411852462
|
17460250853825
|
7
|
2506777.67
|
49
|
6283934288001.1
|
17547443.692
|
5562749.33
|
7687007147860.2
|
9338962784494.7
|
8
|
6913072.998
|
64
|
47790578270408
|
55304583.981
|
5481770.355
|
2669139324440.6
|
2048627255066
|
9
|
6029284.993
|
81
|
36352277528528
|
54263564.938
|
5400791.38
|
562443114971.1
|
395004221862.26
|
10
|
2420120.373
|
100
|
5856982621995.8
|
24201203.735
|
5319812.405
|
8175039187626.5
|
8408213877488.3
|
11
|
5135514.105
|
121
|
26373505120831
|
56490655.153
|
5238833.43
|
20680974590.322
|
10674882947.894
|
12
|
6678073.433
|
144
|
44596664781365
|
80136881.2
|
5157854.455
|
1956503005752.1
|
2311065742205.9
|
13
|
8100689.22
|
169
|
65621165833690
|
105308959.856
|
5076875.48
|
7960107811287.3
|
9143449532154.8
|
14
|
9880557.752
|
196
|
97625421495357
|
138327808.531
|
4995896.505
|
21171362004856
|
23859915499958
|
15
|
7679802.502
|
225
|
58979366468927
|
115197037.529
|
4914917.53
|
5762302235575.1
|
7644588907788
|
16
|
5369042.242
|
256
|
28826614597875
|
85904675.874
|
4833938.555
|
8049557222.061
|
286335955904.14
|
17
|
0
|
289
|
0
|
0
|
4752959.58
|
27871250466749
|
22590624770095
|
18
|
0
|
324
|
0
|
0
|
4671980.605
|
27871250466749
|
21827402774676
|
19
|
0
|
361
|
0
|
0
|
4591001.63
|
27871250466749
|
21077295968034
|
20
|
0
|
400
|
0
|
0
|
4510022.655
|
27871250466749
|
20340304350168
|
Итого
|
105586458.349
|
2870
|
8.3674654087738E+14
|
876252203.43
|
105586458.349
|
2.7932153154239E+14
|
2.4604239578111E+14
|
Шаг 4. Определим компоненту T данной модели. Для этого проведем аналитическое выравнивание ряда (T + E) с помощью линейного тренда. Результаты аналитического выравнивания следующие:
T = 6129602.155 -80978.975t
Подставляя в это уравнение значения t = 1,...,20, найдем уровни T для каждого момента времени (гр. 5 табл.).
t
|
yt
|
Si
|
yt/Si
|
T
|
TxSi
|
E = yt / (T x Si)
|
(yt - T*S)2
|
1
|
5486789
|
0.401
|
13693845.765
|
6048623.18
|
2423535.338
|
2.264
|
9383522995979.5
|
2
|
6556599
|
0.89
|
7363816.89
|
5967644.205
|
5313474.06
|
1.234
|
1545359616412.4
|
3
|
7854524
|
1.283
|
6121141.516
|
5886665.23
|
7553648.81
|
1.04
|
90525880200.11
|
4
|
2154878
|
1.426
|
1511384.407
|
5805686.255
|
8277540.465
|
0.26
|
37486995661169
|
5
|
2548721
|
0.401
|
6361059.678
|
5724707.28
|
2293750.161
|
1.111
|
65010128598.578
|
6
|
8745562
|
0.89
|
9822274.805
|
5643728.305
|
5025065.658
|
1.74
|
13842093034449
|
7
|
3216646
|
1.283
|
2506777.67
|
5562749.33
|
7138006.531
|
0.451
|
15377068411013
|
8
|
9856413
|
1.426
|
6913072.998
|
5481770.355
|
7815712.724
|
1.261
|
4164457616714.9
|
9
|
2415787
|
0.401
|
6029284.993
|
5400791.38
|
2163964.984
|
1.116
|
63414327608.307
|
10
|
2154828
|
0.89
|
2420120.373
|
5319812.405
|
4736657.255
|
0.455
|
6665842302044.6
|
11
|
6589787
|
1.283
|
5135514.105
|
5238833.43
|
6722364.252
|
0.98
|
17576727647.086
|
12
|
9521359
|
1.426
|
6678073.433
|
5157854.455
|
7353884.983
|
1.295
|
4697943615198.2
|
13
|
3245748
|
0.401
|
8100689.22
|
5076875.48
|
2034179.807
|
1.596
|
1467897485673.6
|
14
|
8797456
|
0.89
|
9880557.752
|
4995896.505
|
4448248.853
|
1.978
|
18915602811752
|
15
|
9854566
|
1.283
|
7679802.502
|
4914917.53
|
6306721.973
|
1.563
|
12587197242535
|
16
|
7654989
|
1.426
|
5369042.242
|
4833938.555
|
6892057.242
|
1.111
|
582064867855.09
|
17
|
|
0.401
|
0
|
4752959.58
|
1904394.63
|
0
|
3626718907694.9
|
18
|
|
0.89
|
0
|
4671980.605
|
4159840.45
|
0
|
17304272569558
|
19
|
|
1.283
|
0
|
4591001.63
|
5891079.694
|
0
|
34704819956852
|
20
|
|
1.426
|
0
|
4510022.655
|
6430229.501
|
0
|
41347851429726
|
|
|
|
|
|
|
19.454
|
2.2393623558868E+14
|
Шаг 5. Найдем уровни ряда, умножив значения T на соответствующие значения сезонной компоненты (гр. 6 табл.).
Расчет ошибки в мультипликативной модели производится по формуле:
E = ∑Y/(T * S) = 19.45
Для сравнения мультипликативной модели и других моделей временного ряда можно использовать сумму квадратов абсолютных ошибок:
Среднее значение
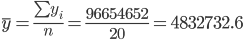
t
|
y
|
(yi-y)2
|
1
|
5486789
|
427789774380.96
|
2
|
6556599
|
2971715365049
|
3
|
7854524
|
9131223265114
|
4
|
2154878
|
7170905258741.2
|
5
|
2548721
|
5216708988934.6
|
6
|
8745562
|
15310233913504
|
7
|
3216646
|
2611735898699.6
|
8
|
9856413
|
25237364761344
|
9
|
2415787
|
5841626033359.4
|
10
|
2154828
|
7171173046701.2
|
11
|
6589787
|
3087240164559.4
|
12
|
9521359
|
21983217518777
|
13
|
3245748
|
2518520120637.2
|
14
|
8797456
|
15719031638508
|
15
|
9854566
|
25218810697356
|
16
|
7654989
|
7965131187341
|
17
|
|
23355304383103
|
18
|
|
23355304383103
|
19
|
|
23355304383103
|
20
|
|
23355304383103
|
Итого
|
96654652
|
2.5100364516542E+14
|
Коэффициент детерминации.
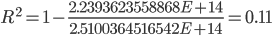
Следовательно, можно сказать, что мультипликативная модель объясняет 11% общей вариации уровней временного ряда.
Проверка адекватности модели данным наблюдения.
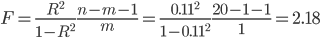
где m - количество факторов в уравнении тренда (m=1).
Fkp = 4.41
Поскольку F < Fkp, то уравнение статистически не значимо
Шаг 6. Прогнозирование по мультипликативной модели. Прогнозное значение Ft уровня временного ряда в мультипликативной модели есть произведение трендовой и сезонной компонент. Для определения трендовой компоненты воспользуемся уравнением тренда:T = 6129602.155 -80978.975t
Прогноз на 1 период:
T21 = 6129602.155 -80978.975*21 = 4429043.68
Значение сезонного компонента за соответствующий период равно: S1 = 0.401
Таким образом, F21 = T21 • S1 = 4429043.68 • 0.401 = 1774609.453 |
|
|
 Скачать 58.84 Kb.
Скачать 58.84 Kb.