Обыкновенные дифференциальные уравнения. Готово Экзамен. Задача Коши для дифференциального уравнения 2го порядка
 Скачать 56.88 Kb. Скачать 56.88 Kb.
|
|
1. Определения дифференциального уравнения 2-го порядка, общего и частного решений. Задача Коши для дифференциального уравнения 2-го порядка. Дифференциальное уравнение 2-го порядка называется диф-ое уравнения включающее независимую переменную Х искомую функцию У и ее производные y’, y’’: F (x, y, y’, y’’) = 0 (1) (1) ДУ в неявном виде Если в ДУ (1) выразить старшую производную y’’, то получим уравнение y’’=f(x, y,y’) (2) (2)-ДУ разрешенное относительно старшей производной О. Уравнение, состоящее в том, что при x=x0, функция y и ее производная y’ примут значения y0 y10 называется начальным условием Об. y(x0)= y0; y’(x0)= y10 (3) О. Общим решением ДУ 2-го порядка называется функция f=f(x, C1,C2), где C1,C2-константы удовлетворяющее следующие условия а)при подстановке в ДУ(1) превращает его в тождество б)каковы бы небыли начальное условие (3) найдутся константы C1= C1*, C2= C2*, такие, что функция f=f(x, C1,C2) будет решением ДУ (1) и будет удовлетворять нач. условию (3) О. Частным решением ДУ2-го порядка (1) называется функция f=f(x, C1,C2), получаемая из общего решения f=f(x, C1,C2) при конкретных значениях констант C1= C1*, C2= C2* Если общее и частное решение ДУ (1) запишем в виде Ф(x, C1,C2)=0; Ф(x, y, C1*, C2*,), то их принято называть общим и частным интегралами О. Задачей Коши называется задача нахождения частного решения ДУ (1) при заданных начальных условиях (3): 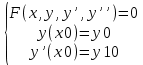 2. Определения дифференциального уравнения n-го порядка, общего и частного решений. Задача Коши для дифференциального уравнения n-го порядка. Для ДУ n-го порядка все понятия и определения аналогичны с определения дифференциального уравнения n-го порядка, т.е. Дифференциальное уравнение n-го порядка называется диф-ое уравнения включающее независимую переменную Х искомую функцию У и ее производные y’, y’’: F (x, y, y’, y’’,…, y(n)) = 0 (1) (1) ДУ n-го порядка в неявном виде Если в ДУ (1) выразить старшую производную y’’, то получим уравнение y(n)=f(x, y,y’,…, y(n-1)) (2) (2)-ДУ n-го порядка, разрешенное относительно старшей производной О. Уравнение, состоящее в том, что при x=x0, функция y и ее производная y’ примут значения y0 y10 называется начальным условием Об. y(x0)= y0; y’(x0)= y10, …, y(n-1)(x0) =yn-1 (3) О. Общим решением ДУ n-го порядка называется функция f=f(x, C1,…,Cn), где C1,C2-константы удовлетворяющее следующие условия а)при подстановке в ДУ(1) превращает его в тождество б)каковы бы небыли начальное условие (3) найдутся константы C1= C1*, C2= C2*, такие, что функция f=f(x, C1,C2) будет решением ДУ (1) и будет удовлетворять нач. условию (3) О. Частным решением ДУ n-го порядка (1) называется функция f=f(x, C1, Cn), получаемая из общего решения f=f(x, C1, Cn) при конкретных значениях констант C1= C1*, Cn = Cn * Если общее и частное решение ДУ (1) запишем в виде Ф(x, C1, Cn)=0; Ф(x, y, C1*, Cn *,), то их принято называть общим и частным интегралами О. Задачей Коши называется задача нахождения частного решения ДУ (1) при заданных начальных условиях (3): 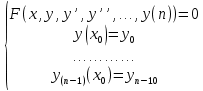 -задача Коши для ДУ n-го порядка ( и n начальных условий) 3. Уравнения, допускающие понижение порядка и решение их. 1) уравнение вида 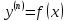 Доказательство. уравнения решаются с помощью последовательного интегрирования 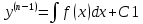 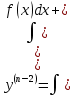 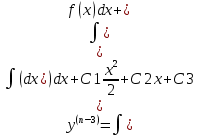 …… Поле n-кратного интегрирования получаем общее решение ДУ: φ=φ(x, C1, …Cn) 2а) Условия вида 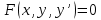 (4) (4)(отличие: отсутствует функция y в явном виде) Чтобы решить уравнение этого вида надо сделать замену: Об. p=y’, p’=y’’ (5) Подставляем (5) в (4) получаем: 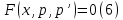 -ДУ 1-го порядка (т.е. показали порядок данного уравнения) Решаем ДУ 1-го порядка (6) известными способами, находим решение p=p(x,C1) , возвращаемся к производной у’ по формуле (5): y’=p(x,C1)- ДУ 1-го порядка с разделяющимися переменными 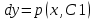 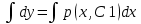 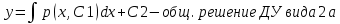 2б) Уравнение вида 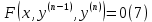 (Отсутствуют в явном виде y,y’,…, 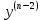 , т.е. присутствуют только две старшие производные) , т.е. присутствуют только две старшие производные)Данное уравнение решается с помощью замены об. 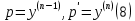 Подставляем в 7, получаем: 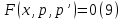 (9)-ДУ 1-го порядка (т.е. понизили порядок данного уравнения (7) Решая его известным методом, получаем общее решение p=p(x,C1) Возвращаемся к У по формуле (8) 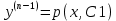 -ДУ допускающее понижение порядка вида 1; общее решение которое получается после (n-1) -кратного интегрирования 3) Уравнение вида 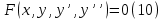 (нет х в явном виде ) Данное уравнение вычисляется с помощью замены: Об. 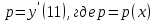 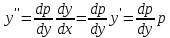 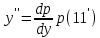 Подставляем (11) (11’) в (10), получаем; 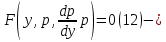 -ДУ 1-го порядка решая его известными методами, получим решение p=p (x, C1) Возвращаемся к функции у по формуле (11): 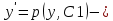 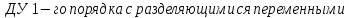 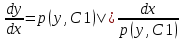 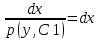 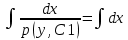 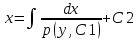 -общее решение допускающее понижение порядка вида 3 4. Определение линейного однородного дифференциального уравнения (ЛОДУ) 2-го порядка. Линейным неоднородным диф. уравнением (ЛНДУ) 2-го порядка называется дифференциальное уравнение вида: 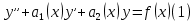 где 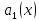 , , 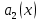 - коэффициенты известные функции - коэффициенты известные функции f(x)- правая часть уравнения тоже известная функция Если правая часть функция f(x)=0 то получаем 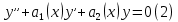 (2)- линейное однородное дифференциальное уравнение (ЛДУ) 2-го порядка Линейным неоднородным дифференциальным уравнением (ЛОДУ) 2-го порядка с постоянными коэффициентами называется диф. уравнением вида: 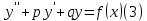 где p,q- коэффициентные числа (известные) f(x)- известная функция Если f(x)=0, то получаем линейное однородное дифференциальное уравнение (ЛОДУ) 2-го порядка с постоянными коэффициентами: 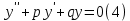 Линейное однородное дифференциальное ур. 2-го порядка Рассмотрим ЛОДУ 2-го порядка 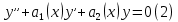 где коэффициентами является функция 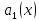 , ,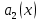 5. Теорема (О линейной комбинации частных решений ЛОДУ) (Док-во). Если функция y1=y1(x), y2=y2(x). Является частным решением ЛОДУ 2-го порядка (2), то функция: 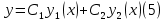 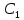 , , 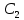 -константа тоже будет решением этого дифференциального уравнения -константа тоже будет решением этого дифференциального уравненияДоказательство: если функция y1=y1(x), y2=y2(x) является частным решением ЛОДУ (2) получаем тождество: 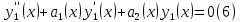 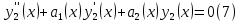 Чтобы функция 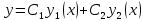 была решением ЛОДУ (2) необходимо доказать, что при подстановке уравнения получается тождество (т.е. равенство нулю): была решением ЛОДУ (2) необходимо доказать, что при подстановке уравнения получается тождество (т.е. равенство нулю):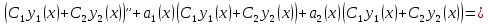 по свойствам производных 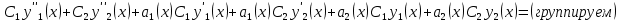 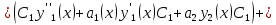 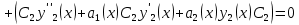 Следовательно функция 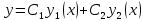 является решением ЛОДУ (2) является решением ЛОДУ (2)6. Определение линейно-зависимых, линейно-независимых функций (2 определения). Функция 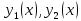 называется линейно независимым на интервале (a,b) если равенство называется линейно независимым на интервале (a,b) если равенство 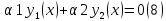 Выполняется только при условии что α1=α2=0 (α1, α2Ꞓ R) Функция y1(x), y2(x) называется линейно не зависимым на интервале (а b) если равенство (8) имеет место к хотя бы одно из чисел 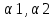 ≠0 ≠0Пусть 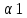 ≠0 тогда получаем: ≠0 тогда получаем: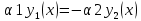 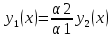 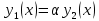 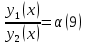 (α=const) Функция 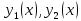 является линейно зависима на интервале ( a b) если они пропорциональны для всех xꞒ(a, b) является линейно зависима на интервале ( a b) если они пропорциональны для всех xꞒ(a, b) 7. Определение определителя Вронского. Теорема (Определеитель Вронского для линейно зависимых (линейно независимых) функций) (Док-во). Определитель Вранского или Вранскиана для диф функции 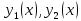 имеет вид имеет вид 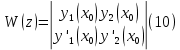 Теорема ( Определитель Вранского для линейно зависимых ): Если функция 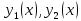 диф-ма линейно зависима на интервале (a d) , то определитель Вранского для этих функций не равен нулю на этом интервале диф-ма линейно зависима на интервале (a d) , то определитель Вранского для этих функций не равен нулю на этом интервале Док-во. Пусть функция 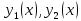 , линейно зависима следовательно по формуле (9) можем записать , линейно зависима следовательно по формуле (9) можем записать  Найдем определитель Вранского для этих функций   ЧТД 8. Теорема (Структура общего решения ЛОДУ 2-го порядка) (Док-во). Если функция  является линейно независимым частным решением ЛОДУ 2-го порядка (2) то функция является линейно независимым частным решением ЛОДУ 2-го порядка (2) то функция 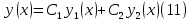  является общим решением этого дифференциального уравнения Доказательство. Согласно определению общего решения дифференциального уравнения должны выполняться 2 условия: 1)При подстановке общего решения дифференциального уравнения получаем тождество 1-е условие доказали в Теореме (10) линейной комбинации частных решений ЛОДУ 2)Из общего решения можно получить единственное частное решение удовлетворяющим заданным начальным условиям 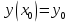 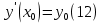 Докажем. Подставляем начальное условие 12 в формулу (11) 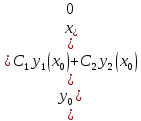 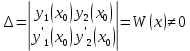 Т.к. функция 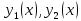 линейно независима по условию теоремы. линейно независима по условию теоремы.Если определитель СЛАУ δ≠0, то она имеет единственное решение 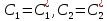 следовательно будет единственное частное решение следовательно будет единственное частное решение 9. Определение ЛОДУ 2-го порядка с постоянными коэффициентами. Характеристическое уравнение ЛОДУ 2-го порядка с постоянными коэффициентами (Вывод). Линейно не зависимая функция 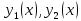 входящее в общее решение ЛОДУ называется функциональной системой решения этого уравнения входящее в общее решение ЛОДУ называется функциональной системой решения этого уравнения Решением ЛОДу 2-го порядка с постоянными коэффициентами Рассмотрим ЛОДУ 2-го порядка: 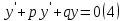 где q, p- числа Будем искать частные решения этого решения в виде: 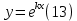 , где k- число , где k- число Подставляем решение (13) в формулу (4) для этого находим производные 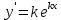 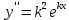 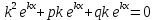 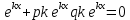 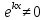 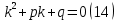 (14)-характеристическое уравнение ЛОДУ 2-го порядка вида (4) имеет место при вида решений ЛОДУ в зависимости от корней характеристического уравнения действительны и различны (D>0): 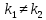 , , 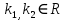 Получаем частное решение: 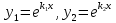 Докажем линейную независимость этих решений по формуле (9): 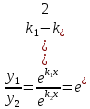 Следовательно, 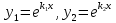 фундаментальные системы решений в данном случае фундаментальные системы решений в данном случае Таким образом получаем общее решение однородного уравнения: 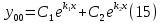 2)Корни характеритсического уравнения действительны и равные (D=0) 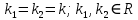 Частные решения будут иметь вид: 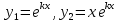 Докажем их ленйную независимость по формуле (9) 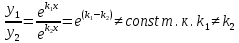 Следовательно, 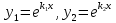 фундаментальные системы решения в данном случае фундаментальные системы решения в данном случае Таким образом получаем общее решение однородного уравнения: 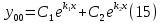 10. Решение ЛОДУ 2-го порядка с постоянными коэффициентами (3 случая). Рассмотри ЛОДУ 2-го порядка: 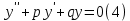 где p,q-числа Будем искать частные решения этого уравнения в виде: 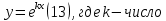 Подставим (13) в (4) 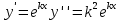 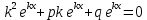 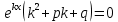 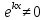 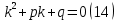 (14)- характеристическое уравнение ЛОДУ 2-го порядка (4) Имеет только 3 вида решения ЛОДУ в зависимости от корней характеристического уравнения 1. Корни характеристического уравнения действительны и различны (p>0): k1≠k2; k1, k2∈R Получаем частное решение из формулы (13): 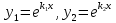 Докажем линейную независимость этих решений по 2-му определению линейной независимости: 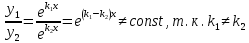 следовательно 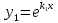 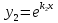 - фундаментальная система решений в данном случае - фундаментальная система решений в данном случае Таким образом получаем общее решение однородного уравнения: 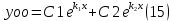 2) корни характеристического уравнения действительные и равные (D=0): 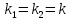 ; k1, k2 ∈ R ; k1, k2 ∈ RЧастные решения будут иметь вид 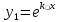 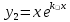 Докажем их линейную независимость 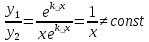 Следовательно, 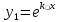 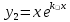 - фундаментальные системы решений в этом случае - фундаментальные системы решений в этом случае 3.Корни характеристического уравнения комплексно сопряженные: 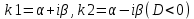 Частные решения ЛОДУ будут иметь вид: 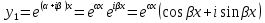 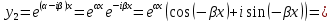 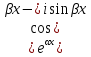 Частные решения в комплексных числах не очень подходят для ДУ в действительном анализе, поэтому частные решения будем искать 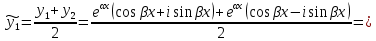 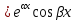 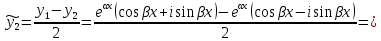 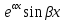 Получим частное решение 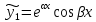 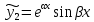 Проверим их линейную независимость 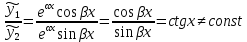   общее решение в этом случае (D<0) 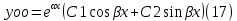 11. Определение линейного неоднородного дифференциального уравнения 2-го порядка (ЛНДУ). Теорема (Структура общего решения ЛНДУ) (Док-во). Рассмотри ЛОДУ 2-го порядка 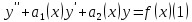 Если соответствует ЛОДУ 2-го порядка 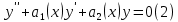 Теорема (Структура общего решения ЛОДУ 2-го порядка : общее решение  линейного неоднородного ДУ (1) является суммой частного решения линейного неоднородного ДУ (1) является суммой частного решения  этого уравнения, а общее решение этого уравнения, а общее решение  соответствующего ДУ (2) соответствующего ДУ (2) Доказательство. По определению общего решения ДУ надо дописать 2 условия: 1)  должна удовлетворять ЛНДУ(1) должна удовлетворять ЛНДУ(1)По условию теоремы  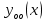 является решением ЛНДУ (1) и ЛОДУ (2) соответственно, следовательно, справедливо равенство является решением ЛНДУ (1) и ЛОДУ (2) соответственно, следовательно, справедливо равенство 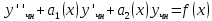 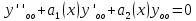 Складываем почтенно полученные уравнения: 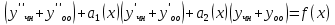 По свойству производных получаем:  т.е.  удовлетворяет ЛНДУ 2-го порядка, следовательно является решением удовлетворяет ЛНДУ 2-го порядка, следовательно является решением  2) Докажем, что решение  где 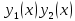 – независимые функции, дает единственное частное решение ЛНДУ 2-го порядка, удовлетворяющее начальному условию явл. – независимые функции, дает единственное частное решение ЛНДУ 2-го порядка, удовлетворяющее начальному условию явл.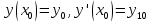 Подставим начальное условие в (19). Для этого найдем производную 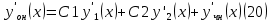 в (19) и (20) 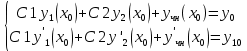 Получим СЛАУ из 2-х уравнений с 2-мя неизвестными С1 и С2 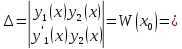 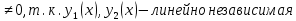 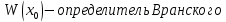 Если определитель суммы 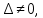 то она имеет единственное решение: то она имеет единственное решение: 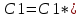 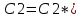 , следовательно будет единственное частное решение удовлетворяющее начальному условиям , следовательно будет единственное частное решение удовлетворяющее начальному условиям Т.о. получили:  12. Теорема (О наложении решение) (Док-во). Теорема (О наложении решений): Если  -частное решение уравнения: -частное решение уравнения: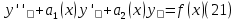 Тогда 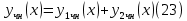 является частным решением : является частным решением :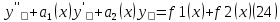 Доказательство: По условию теоремы 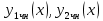 -является решением уравнения (21) (22), соответственно, справедливы равенства: -является решением уравнения (21) (22), соответственно, справедливы равенства:В (21) подставляем  в (22) в (22)  Складываем почтенно:   По свойству производных:   -Является частным решением ДУ (24) 13. Определение ЛНДУ 2-го порядка с постоянными коэффициентами. Решение ЛНДУ 2-го порядка с постоянными коэффициентами и правой частью специального вида (два случая). Рассмотри ЛНДУ 2-го порядка с постоянными коэффициентами  и соответствующего ему ЛОДУ  Структура общего решения ЛНДУ 2-го порядка:     Частное решение ЛНДУ с постоянными коэффициентами специального вида Правая часть вида 1:  , ,  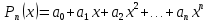 многочлен степени n Частное решение будем искать по формуле: 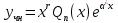 где r- кратность числа 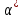 , как корня характеристического уравнения , как корня характеристического уравнения  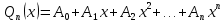 многочлен степени n где 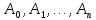 - коэффициенты, которые будем искать методом неопределенных коэффициентов - коэффициенты, которые будем искать методом неопределенных коэффициентов Правая часть вида 2: 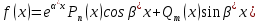  Частное решение для данной правой части 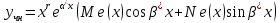 где r- кратность числа 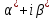 корни характеристического уравнения корни характеристического уравнения 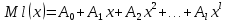 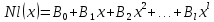 где l- многочлены, l=max(n,m) 14. Определение и решение линейных однородных дифференциальных уравнений 3-го порядка и выше. Линейные однородные дифференциальные уравнения высших порядков (больше 3) Рассмотрим ЛОДУ n-го порядка 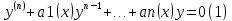 Все опред. понятия теории из теории для ЛОДУ-2-го порядка можно перенести на ур (1) Если функция y1=y2(x); y2=y2(x),…,yn=yn(x) является частным решение для ЛОДУ можно перенести на ур (1) Если функция y1=y1(x); y2=y2(x),…,yn=yn(x) является частым решением для ЛОДУ (1) по фонкц. y=C1y1+C2y2+…+Cn yn является решением, где C1,C2,…,Cn-const, функция y1(x), …, yn(x) называется линейно зависимым на (а.в) или равенство α1y(x)+…+αn yn(x)=0, хотя бы одни из констант α1,…,αn≠0 Определитель Вронского для дифференциальной функции y1(x), …, yn(x) имеет вид 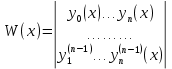 Структура общего решения ЛОДУ (1) Если y1(x) , yn линейно независимые частные решения ЛОДУ (n-го порядка) то 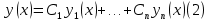 Будет общим решением ЛОДУ (C1,C2,…,Cn-const) ЛОДУ n-го порядка с постоянным коэффициентом имеет вид 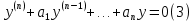 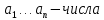 Схема решения ЛОДУ (3) записываем характеристики уравнения для данного ЛОДУ  в зависимости от корней частным решением будет следующее а) Если имеет дейсв. корень К кратности 1 получаем, решение имеет вид  б) Если имеются комплексное сопряженные корни равные  частные решения имеют вид  в) Если имеется действительный корень К кратности r, то получаем следующее частное решение  , ,  г) если имеются комплексно-сопряженные корни равные  получаем след 2m частные решения   Записываем общее решение 15. Метод Лагранжа решения ЛНДУ 2-го порядка (Вывод). Метод Лагранжа (вариации производных состояний Рассмотрим ЛНДУ 2-шо порядка  Решаем методом Лагранжа запишем соответствующее ЛОДУ  Находим общее решение ЛОДУ (5)  где 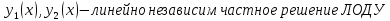 Вместо констант С1 С2 общее решение (6) подставляем ф-ции 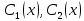 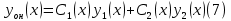 (7) – общее решения неоднород. решен. Находим 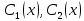 16. Практическое задание: Приближенное решение дифференциальных уравнений с помощью рядов Тейлора (Маклорена) |
